«Недавно я начал экспериментировать с gnuplot и быстро сделал интересное открытие. Я построил все простые числа ниже 1 миллиона в полярных координатах, так что для каждого простого p (r, ?) = (p, p). Ничего особенного не ожидал, просто пробовал. Результаты впечатляют».
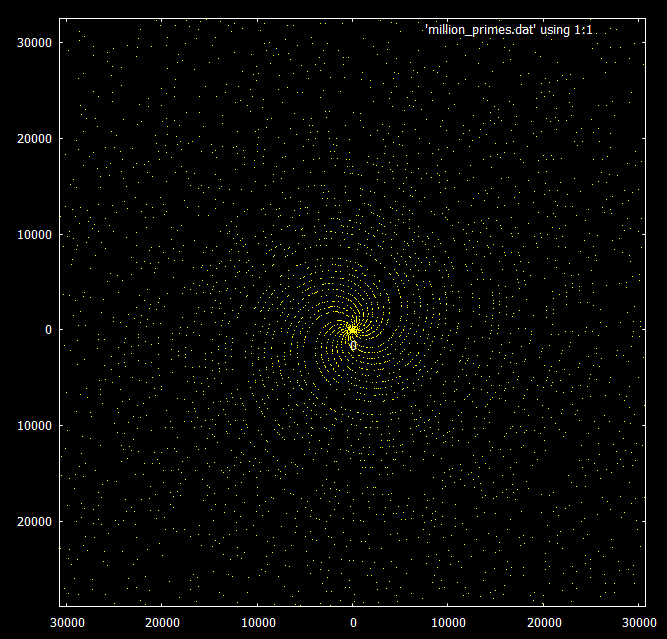
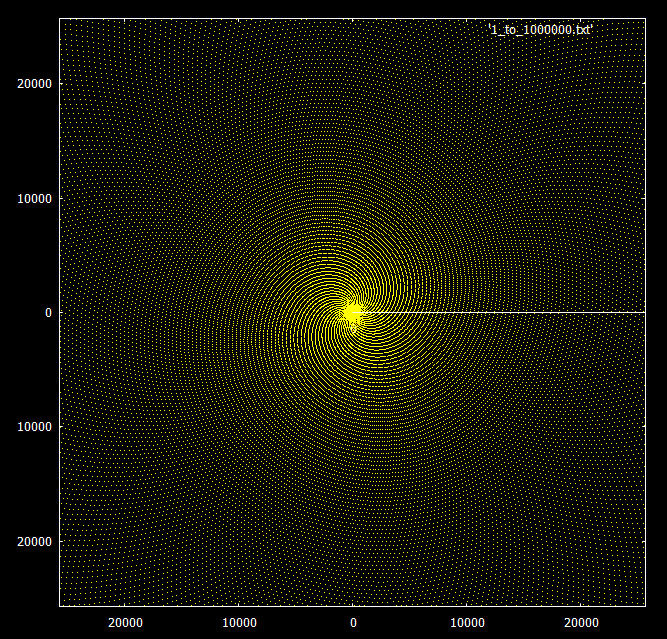
Если посмотреть на простые числа ниже 30000, можно увидеть спиральный узор.
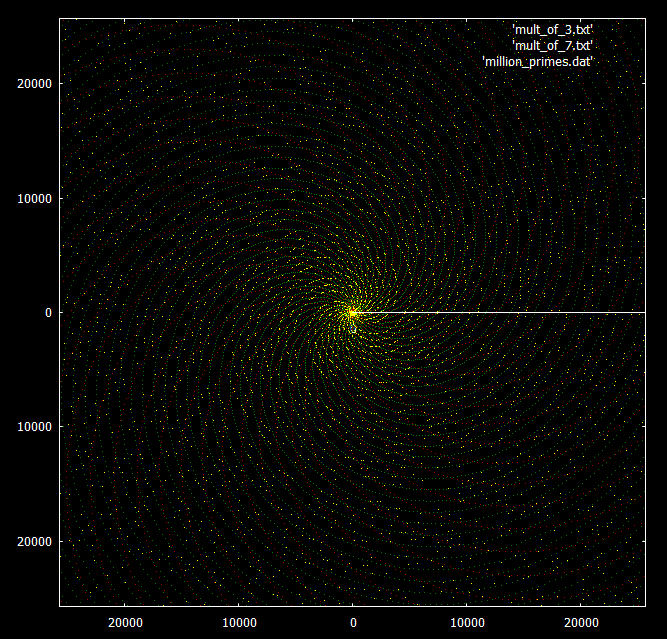
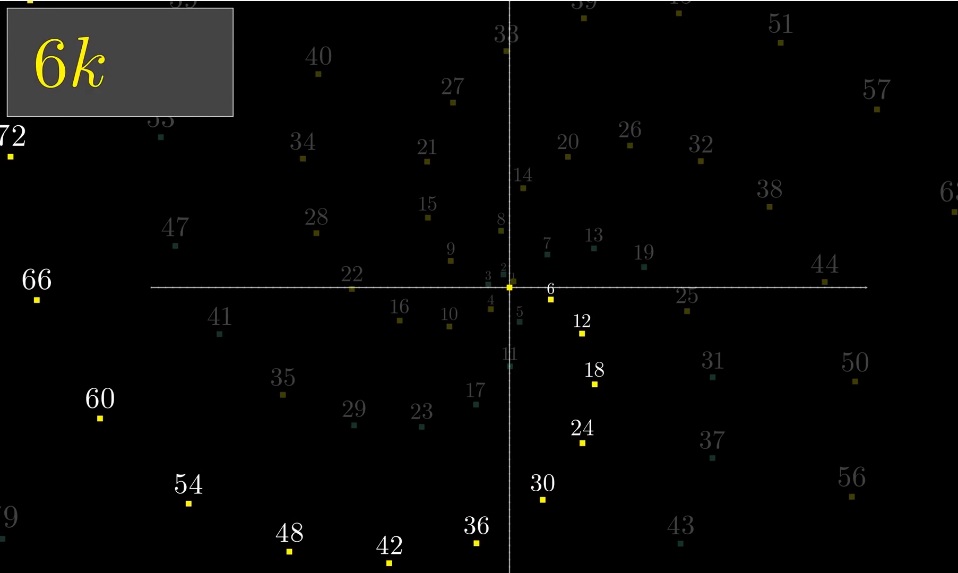
Для сравнения — тот же график с наложенными на него числами, кратными 3 и 7. Простые числа выделены желтым цветом, кратные 3 и 7 — зеленым и красным соответственно.

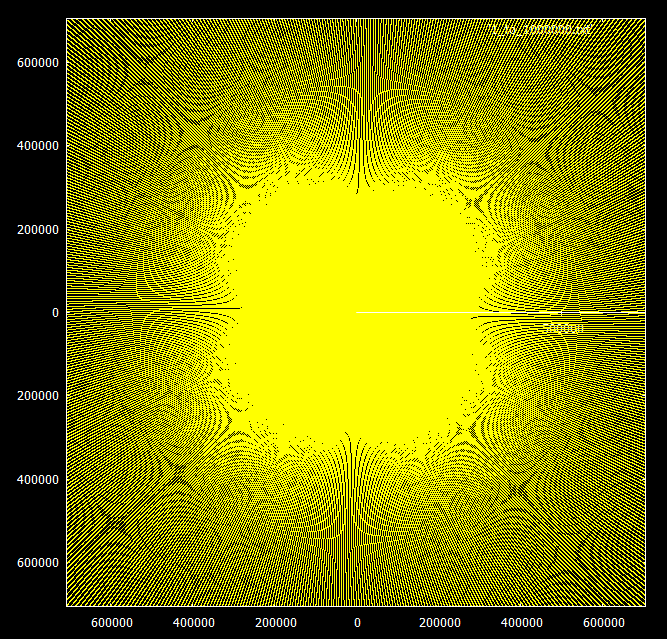
Что действительно интересно, так это поведение при увеличении диапазона. Кратные данного числа кажутся спиралевидными по той же схеме в бесконечность, но простые числа начинают образовывать лучи группами по 3 или 4.
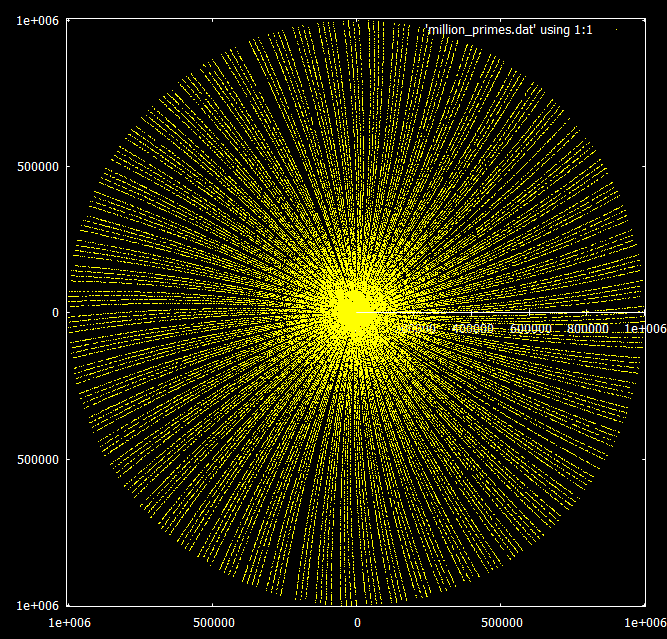
По сравнению с числами, кратными 3 и 7:
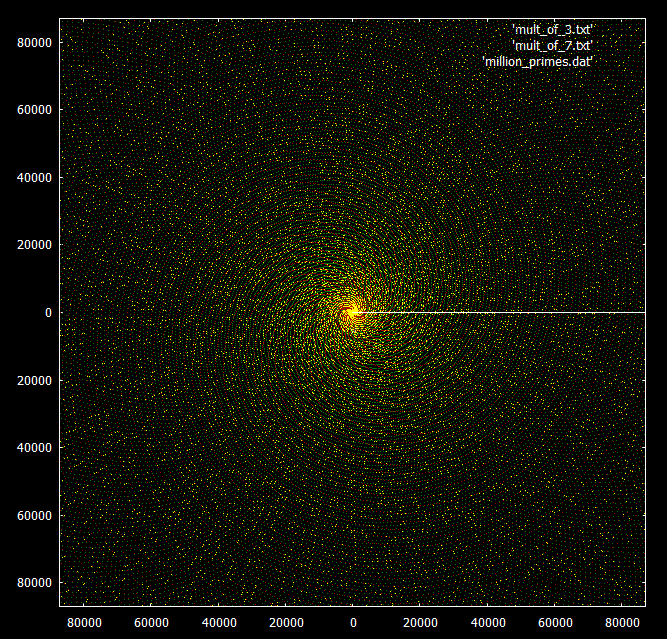
Связаны ли эти закономерности с теоремой о простых числах? Являются ли эти лучи тем же явлением, что и диагональные линии в Скатерти Улама?
В ответ на объяснение Грега Мартина я решил добавить еще пару графиков. Чтобы понять, почему они актуальны, прочтите его ответ.
(г, ?) = (n, n), n?N
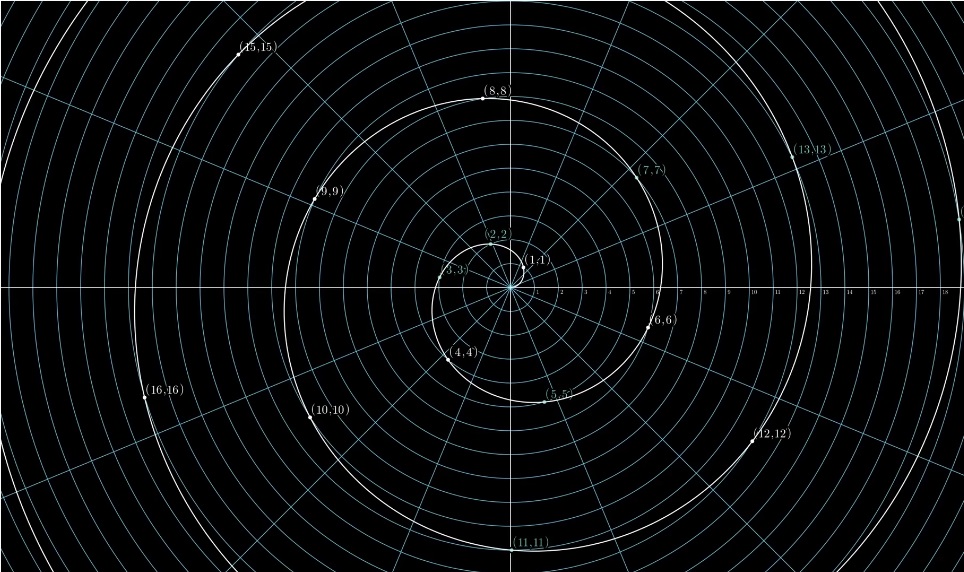
Для начала можно поиграться с полярными координатами и рассмотреть все точки с целочисленными координатами: (1,1) (2,2)…
Получаем Архимедову Спираль:
Если исключить все числа, кроме простых, то получаем спиральную галактику с пробелами:
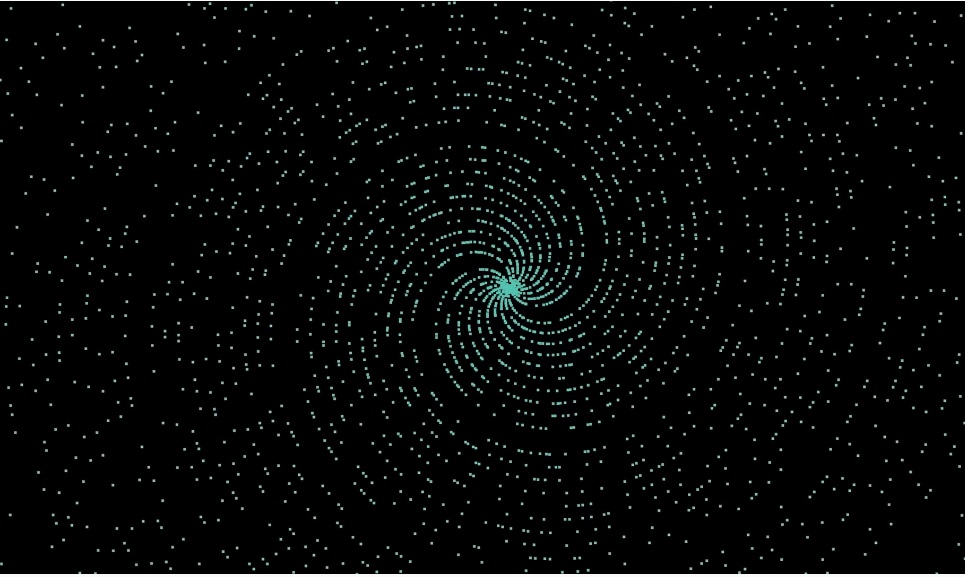
«Отдаляясь» мы можем увидеть направленные во все стороны лучи, по большей части в группах по 4 штуки:

Спирали можно посчитать, их 20 штук:

А лучей 280:

Если брать все числа, а не только простые, то спирали поровнее и их 44:

При самом близком рассмотрении у нас 6 спиралей:

Все числа, кратные 6 образуют одну ветку:
Остальные рукава спиралей 6к+1, 6к+2 и тд. Почему так? Потому что 6 примерно равно (полному обороту) 2? (6.28318530718). Эта маленькая разница создает иллюзию единой кривой.
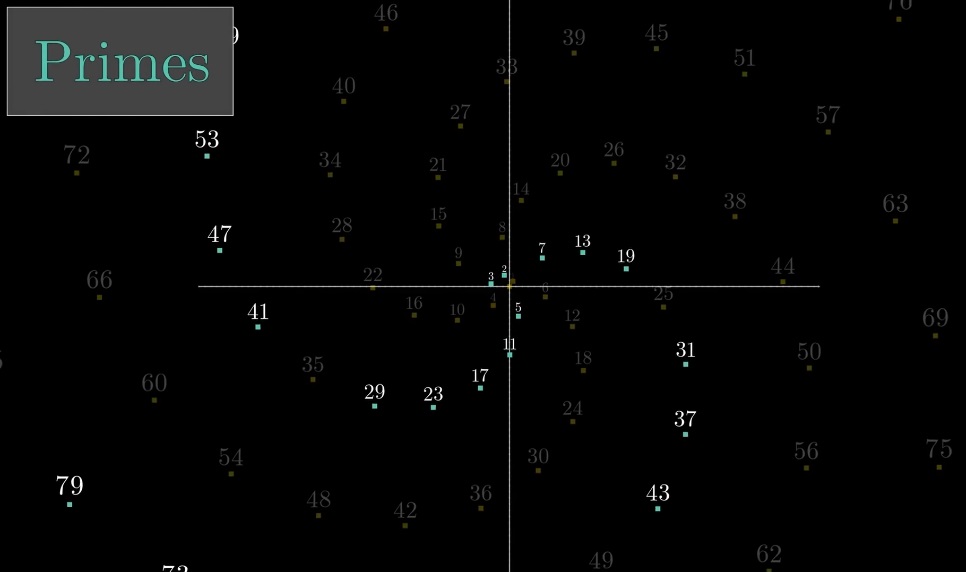
Если оставить только простые числа, останется только две спирали (6к+1 и 6к+5):
6 — почти полный круг, 44 — еще более точное приближение (44/2? ? 7 полных кругов)
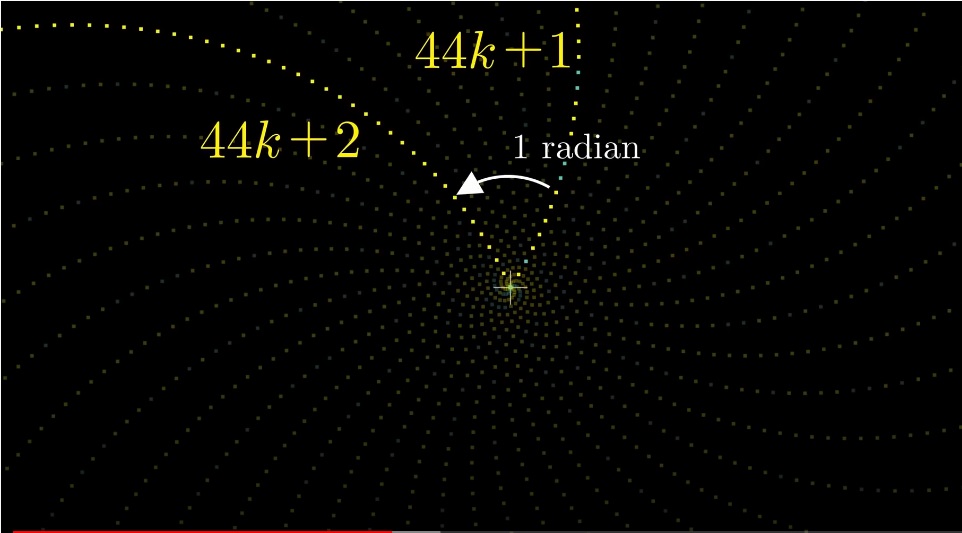
Только для простых чисел остается 20 рукавов (44к+1, 44к+3, 44к+5...). Функция Эйлера ? (44) = 20.

710/2? ? 113. (113,00000959)

Для простых чисел будут пробелы:

Чем дальше отдаляемся, тем отчетливее проявляется кривизна всей структуры.
710=71*5*2. Это объясняет группировку по 4 луча (5) и «отломанные зубцы расчески» (71):

Функция Эйлера ? (710) = 280.
По теореме Дирихле, простые числа равномерно распределятся по рукавам.
Вывод
Играясь с визуализацией, можно наткнуться на а) принцип Дирихле б) на приближения числа ? (и цепные дроби) в) дойти до функции Эйлера.
Спиралевидная форма — это артефакт, связанный с совпадением с четным числом радианов.
Ролик с русской озвучкой:
P.S.
Еще работы по простым числам:
- Bounded gaps between primes. (By Yitang Zhang, 2014)
- Primes in tuples I (By DANIEL A. GOLDSTON, JANOS PINTZ, and CEM Y. YILDIRIM, 2009)
Цепные дроби от Савватеева:
Алексей Савватеев «Все о записи чисел»:






200sx_Pilot
А как всё это выглядит в трехмерной системе координат?
gulinvse
На трёхмерное пространство есть два способа обобщить: систему координат брать цилиндрическую (\rho,\phi,z)=(p,p,p) для простых p или сферическую (r,\phi,\theta)=(р, р, р). С цилиндрической всё проще: получатся те же 280 лучей (которые постепенно поворачиваются), но лежать они будут в конусе с уравнением z^2=x^2+y^2 (другими словами конус этот это множество точек, равноудалённых от оси z и плоскости xOy, потому что для \rho=v(x^2+y^2) и для z мы берём одно и то же значение p). В сферической системе сложнее, по скольку круги наматывают не только в горизонтальном круге вокруг оси Oz посредством увеличения \phi, но и в вертикальных кругах посредством увеличения \theta, которое отсчитывается от оси z. Тут сложнее сказать как получается.
200sx_Pilot
Интереснее сфера, т.к. цилиндр — это всё-таки псевдообъём, как мне кажется.