Лучший способ объяснить школьникам и самому себе, что такое фазовое (конфигурационное) пространство.
Дано: Два блока массой 1 кг и 100 (10 000, 1 000 000,… 100x) кг. Трение в системе отсутствует, удары абсолютно упругие (потерь энергии нет). Более массивный блок ударяет менее массивный и тот отскакивает от него, а потом от стенки слева. Справа стены нет, тела могут двигаться в бесконечность.
Вопрос: Сколько столкновений совершит маленький блок, пока система не придет в состояние, когда столкновения невозможны (скорость маленького тела меньше скорости большого, двигающегося в бесконечность)?
Ответ невероятен:
В очередной раз поражаюсь изящности объяснений от 3Blue1Brown. Предлагаю читабельный конспект с небольшими сокращениями и дополнениями.
В случае когда массы равны, мы насчитаем 3 столкновения:
Если разница масс в 100 раз, то количество столкновений 31:
Если разница масс в 10 000 раз, то столкновений будет 314:
+ еще один удар об стенку
Если разница в 1 000 000 раз, то столкновений 3141:
Если разница в 100 000 000 раз, то столкновений 31415:
Если разница в 10 000 000 000 раз, то столкновений 314159:
Эта закономерность была открыта Григорием Гальпериным в 1995 и опубликована в 2003 году:
PLAYING POOL WITH ? (2003)
Данный метод позволяет построить «физическую» машину вычисления числа ? с точностью до n-ного знака. Разница масс должна составлять 100(n-1) раз.
С реализацией, конечно, есть нюансы, ну да ладно. Зато красивая идея.
Throwing ? at a wall (2006)
Механическая система описывается двумя законами сохранения: энергии и импульса.
Фазовое пространство для энергии системы представляет собой эллипс, но его можно откалибровать корнем из разницы масс:
Радиус окружности показывает энергию в системе — она всегда постоянная.
При столкновении двух блоков происходит перераспределение импульса и энергии:
Закон сохранения моментов задает угол наклона:
При ударе об стену (объект бесконечной массы) скорость блока меняется на противоположную:
Следующее соударение блоков:
Последующие столкновения:
Фазовая диаграмма удобна тем, что наглядно кодирует состояние системы:
Если присмотреться, можно заметить, что «столкновения» делят окружность на равные дуги. По теореме о вписанном угле. Встает вопрос, сколько дуг получится на окружности?
Всего длина окружности 2?, а длина дуги определяется половиной угла, который равен соотношению корней из масс блоков (чем больше разница — тем меньше угол). Порядок разницы масс будет определять «точность» ?: 3, 31, 314
еще конспект от 3Blue1Brown:
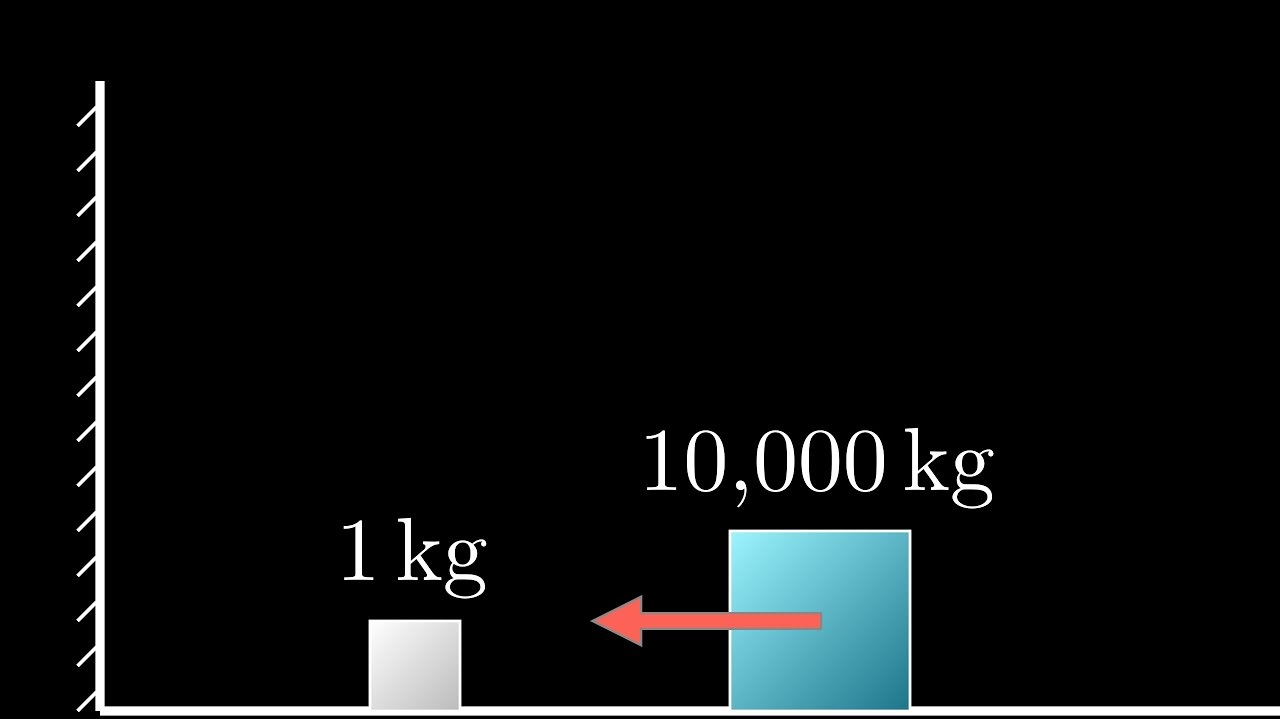
Дано: Два блока массой 1 кг и 100 (10 000, 1 000 000,… 100x) кг. Трение в системе отсутствует, удары абсолютно упругие (потерь энергии нет). Более массивный блок ударяет менее массивный и тот отскакивает от него, а потом от стенки слева. Справа стены нет, тела могут двигаться в бесконечность.
Вопрос: Сколько столкновений совершит маленький блок, пока система не придет в состояние, когда столкновения невозможны (скорость маленького тела меньше скорости большого, двигающегося в бесконечность)?
Ответ невероятен:
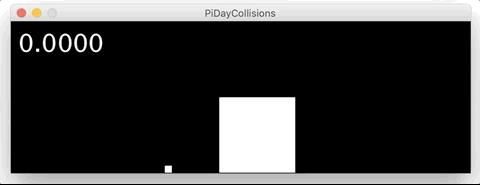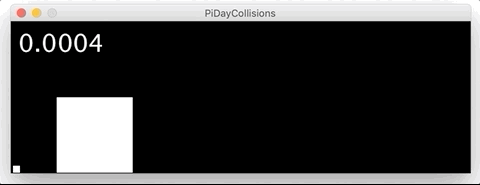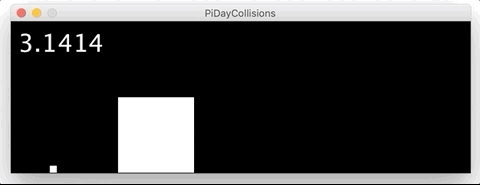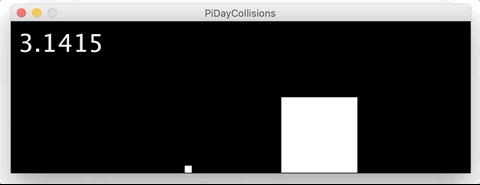
В очередной раз поражаюсь изящности объяснений от 3Blue1Brown. Предлагаю читабельный конспект с небольшими сокращениями и дополнениями.
В случае когда массы равны, мы насчитаем 3 столкновения:
Если разница масс в 100 раз, то количество столкновений 31:
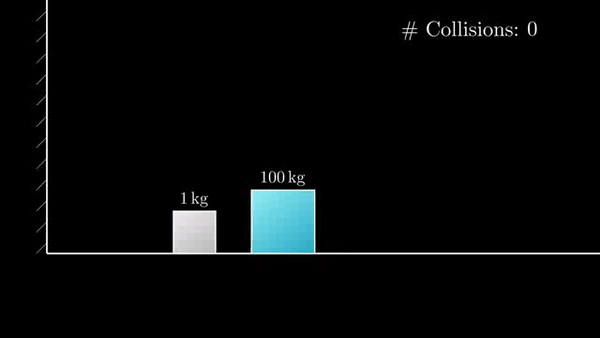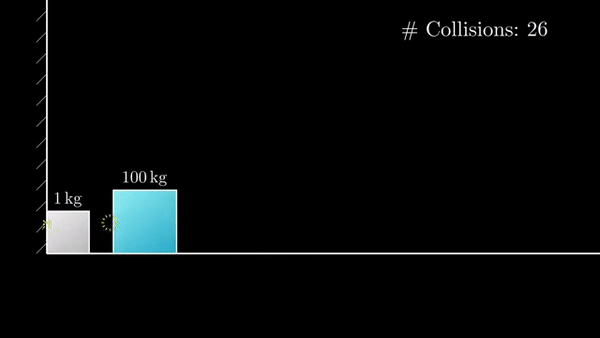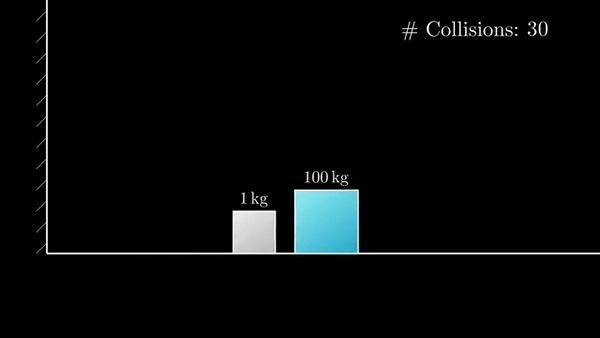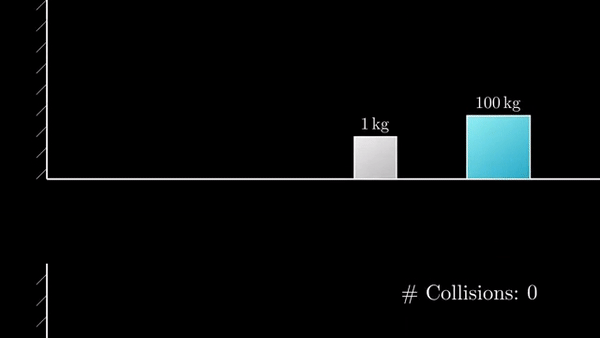
Если разница масс в 10 000 раз, то столкновений будет 314:
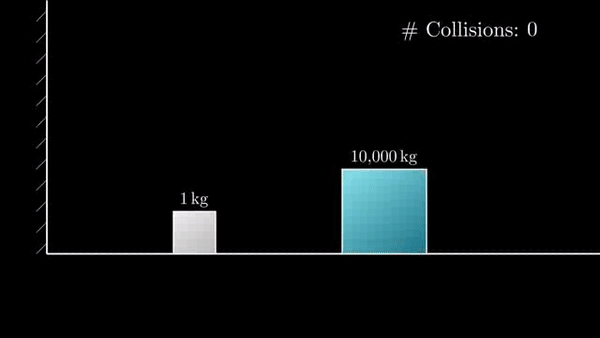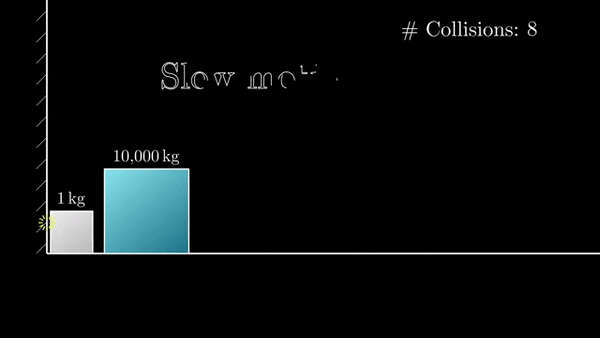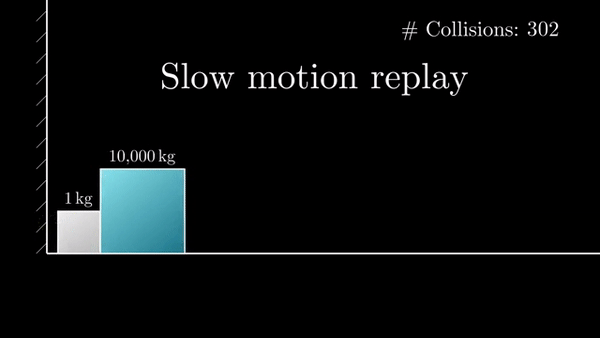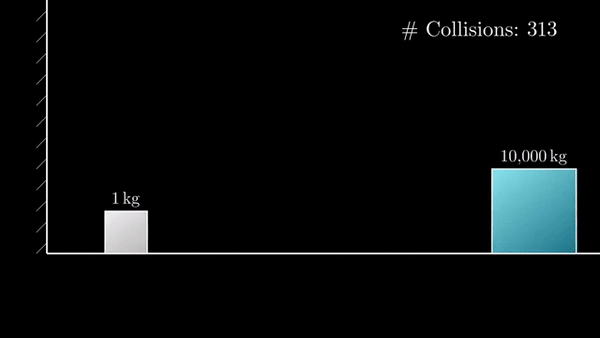
+ еще один удар об стенку
Если разница в 1 000 000 раз, то столкновений 3141:
Если разница в 100 000 000 раз, то столкновений 31415:
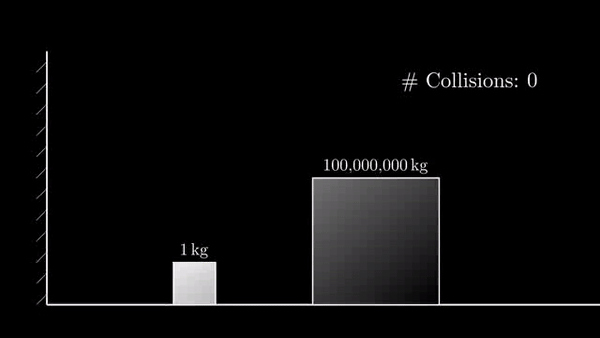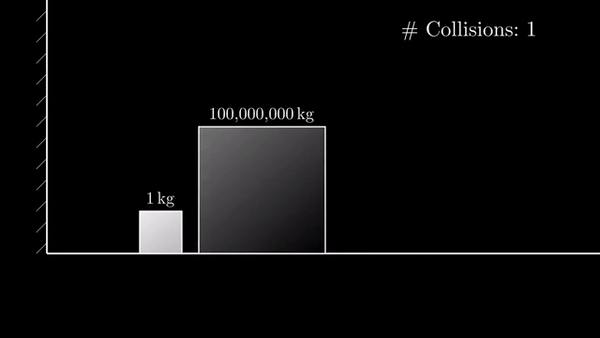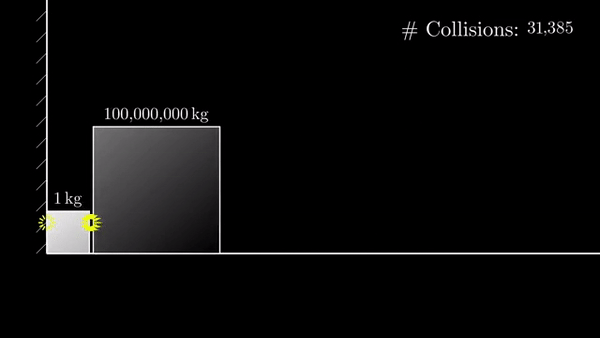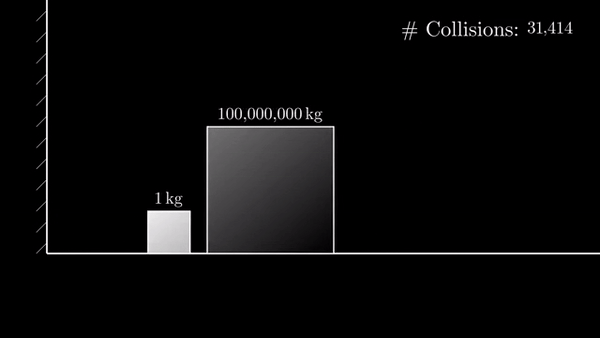
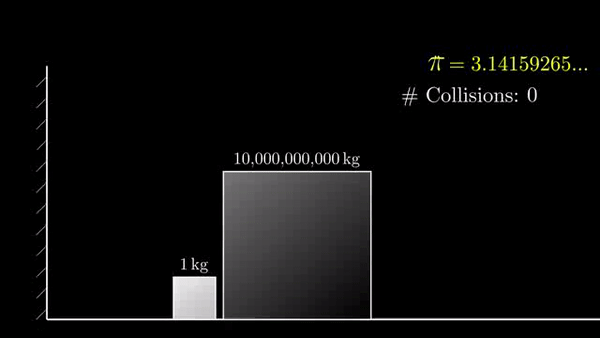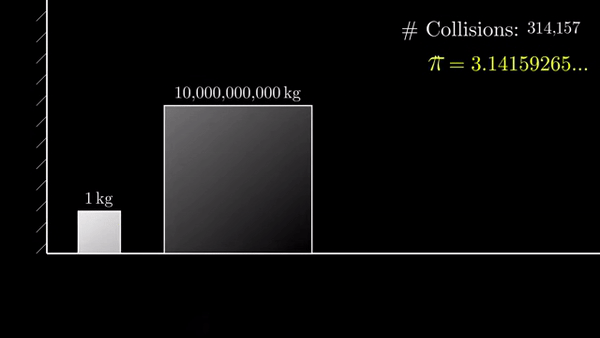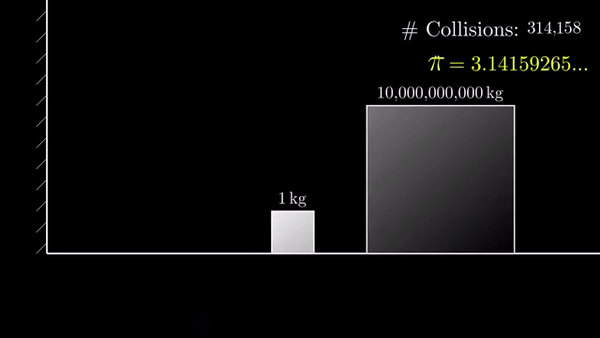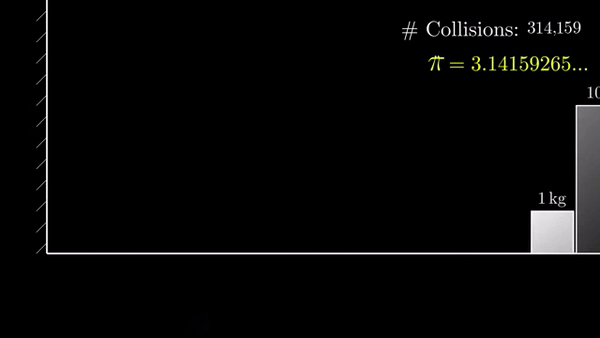
Если разница в 10 000 000 000 раз, то столкновений 314159:
Эта закономерность была открыта Григорием Гальпериным в 1995 и опубликована в 2003 году:
PLAYING POOL WITH ? (2003)
Данный метод позволяет построить «физическую» машину вычисления числа ? с точностью до n-ного знака. Разница масс должна составлять 100(n-1) раз.
С реализацией, конечно, есть нюансы, ну да ладно. Зато красивая идея.
Throwing ? at a wall (2006)
Фазовое/конфигурационное пространство
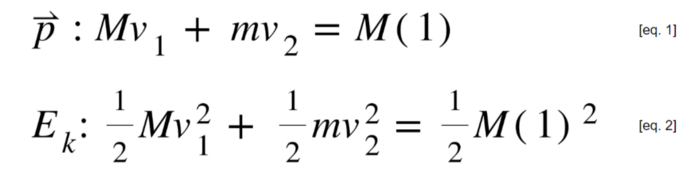
Механическая система описывается двумя законами сохранения: энергии и импульса.
Фазовое пространство для энергии системы представляет собой эллипс, но его можно откалибровать корнем из разницы масс:
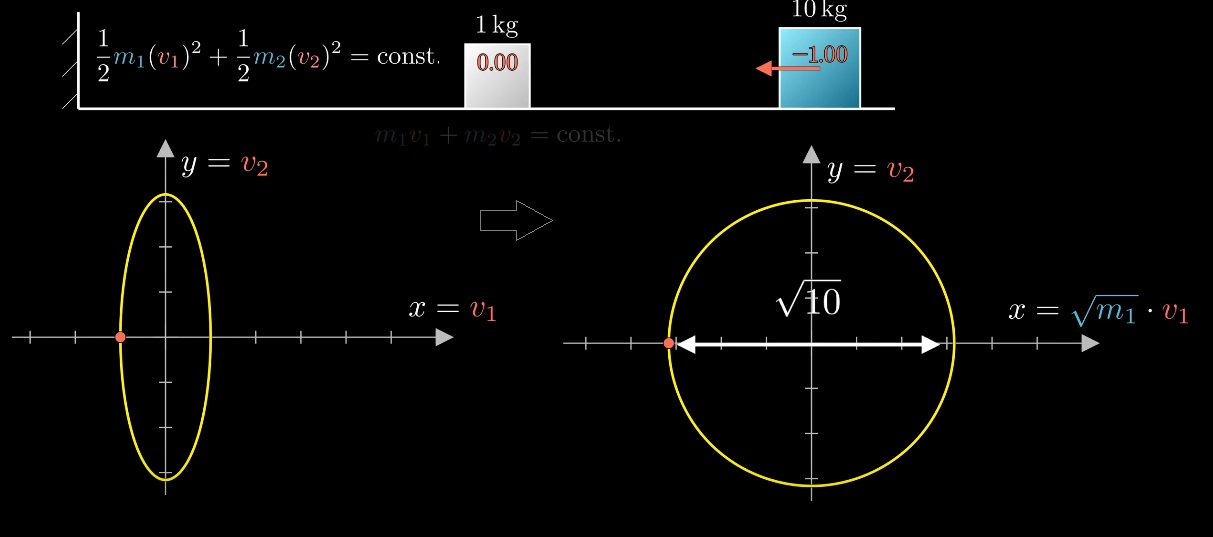
Радиус окружности показывает энергию в системе — она всегда постоянная.
При столкновении двух блоков происходит перераспределение импульса и энергии:
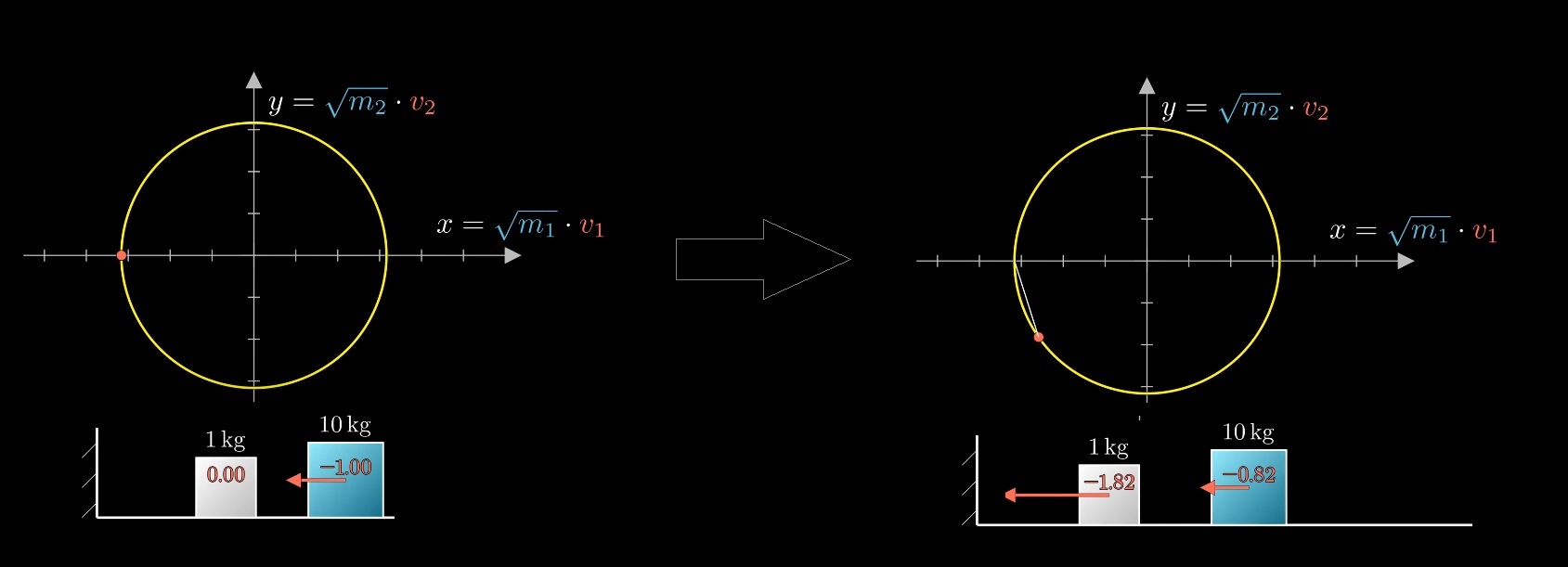
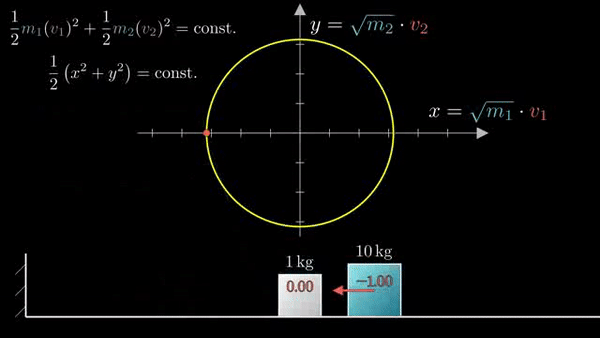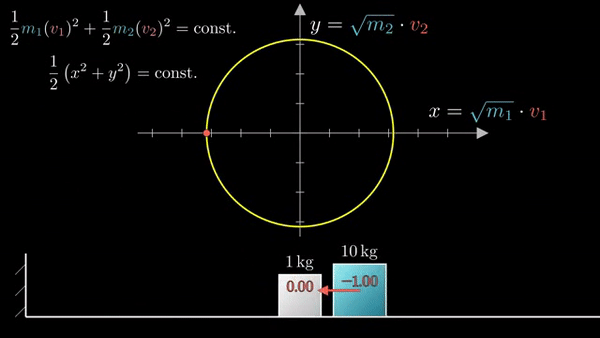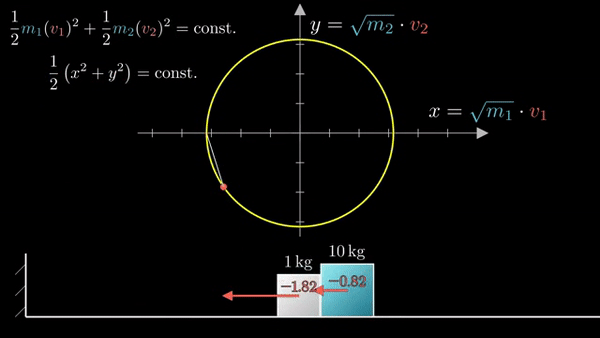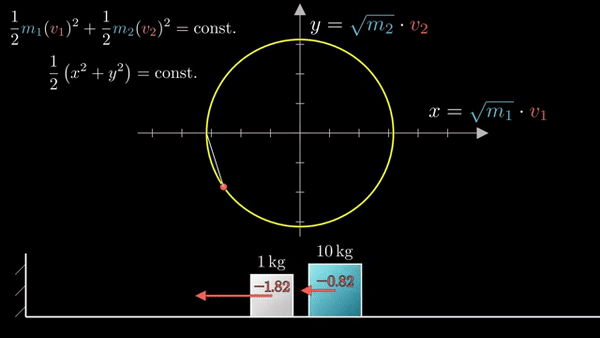
Закон сохранения моментов задает угол наклона:
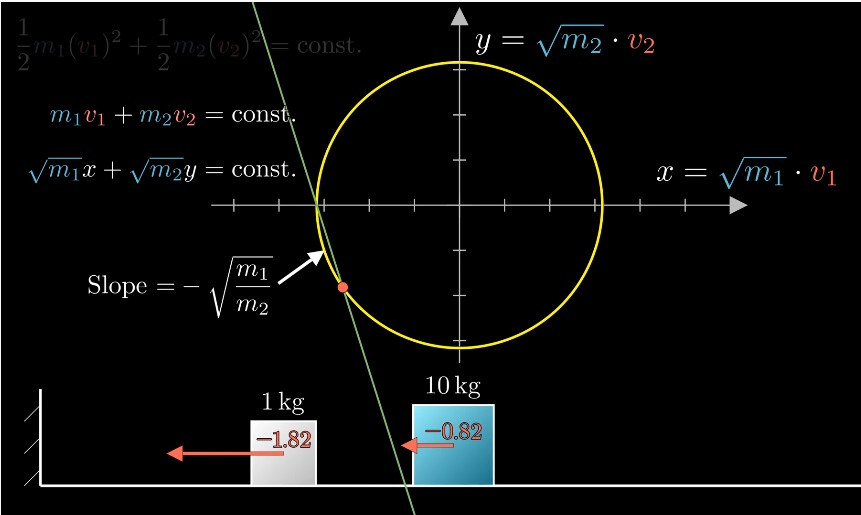
При ударе об стену (объект бесконечной массы) скорость блока меняется на противоположную:
Следующее соударение блоков:
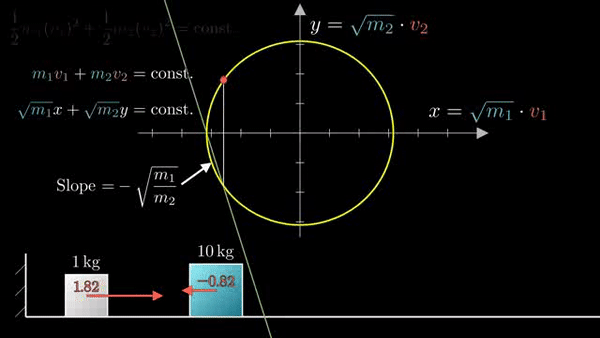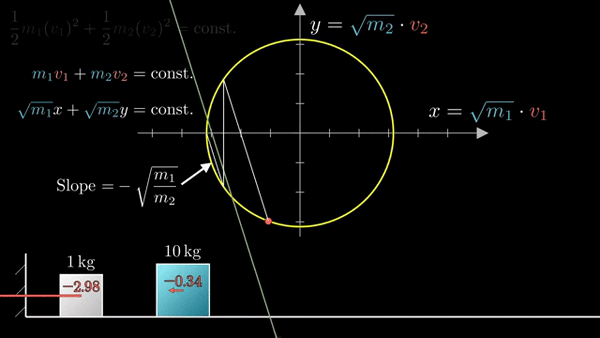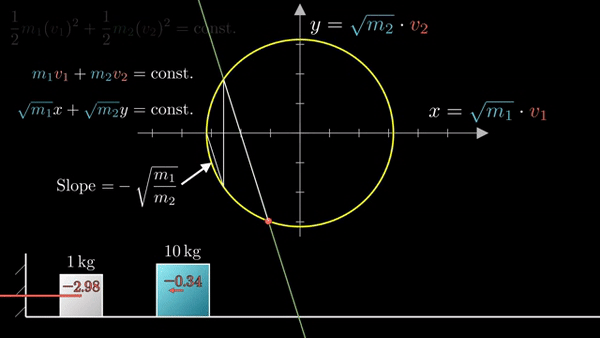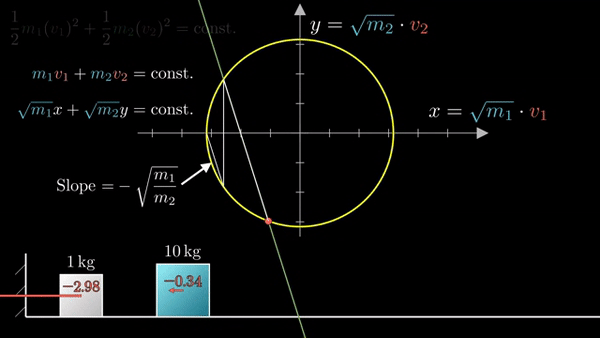
Последующие столкновения:
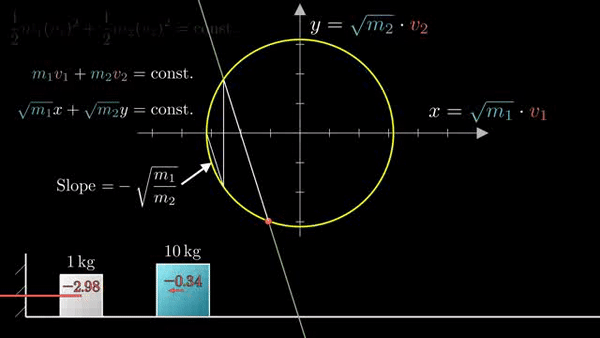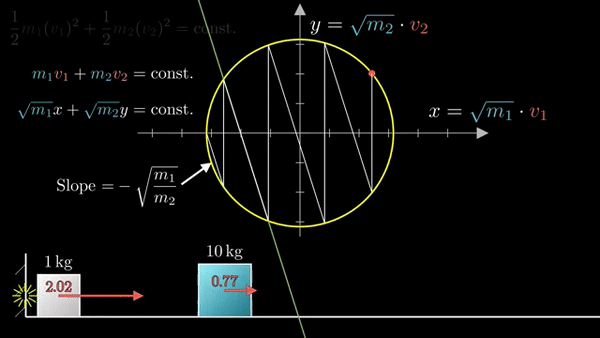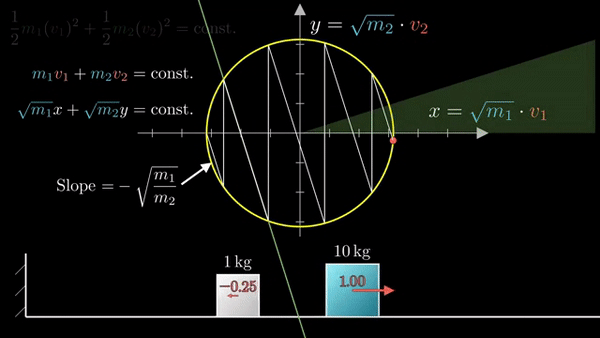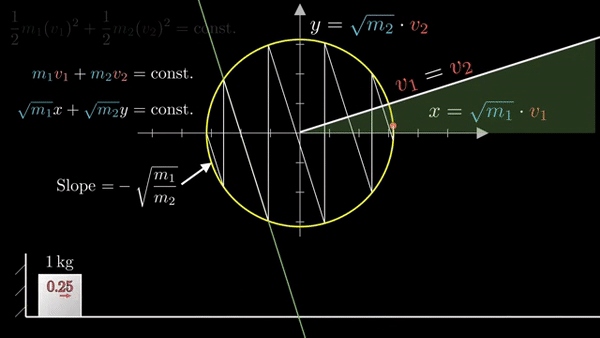
Фазовая диаграмма удобна тем, что наглядно кодирует состояние системы:
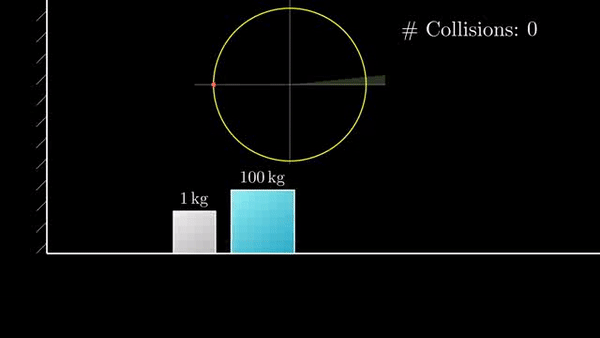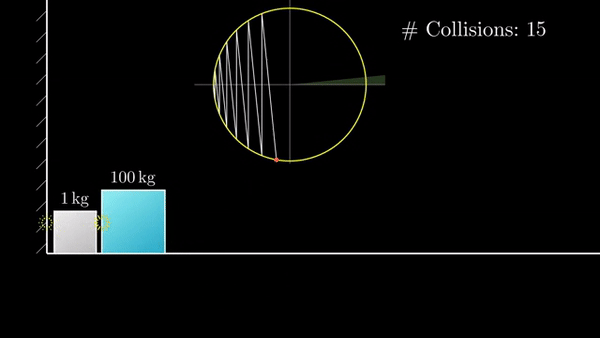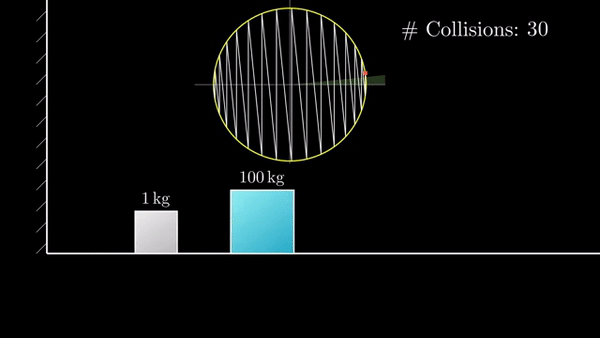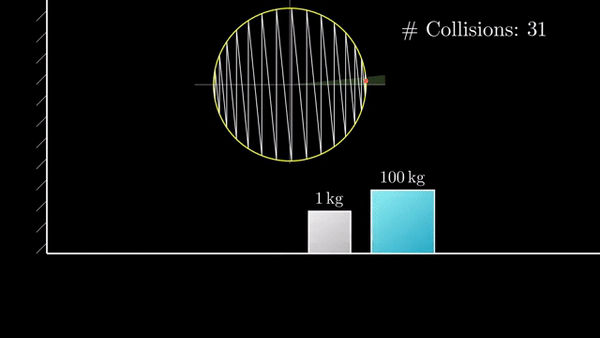
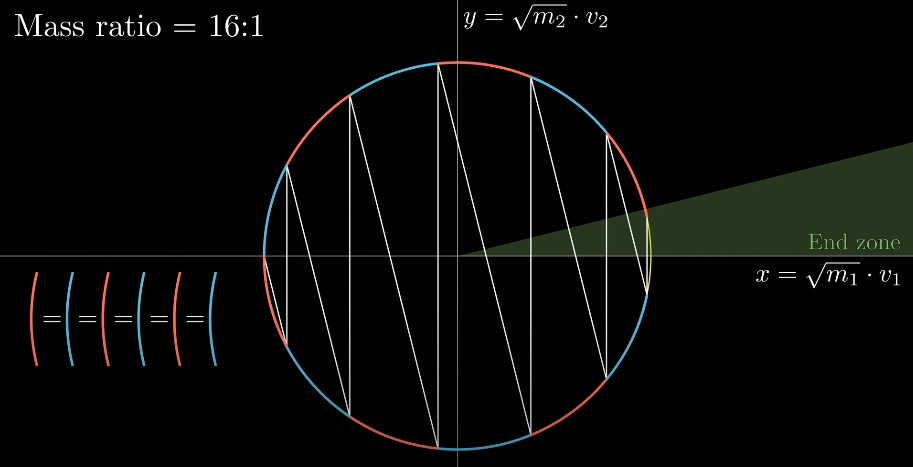
Если присмотреться, можно заметить, что «столкновения» делят окружность на равные дуги. По теореме о вписанном угле. Встает вопрос, сколько дуг получится на окружности?
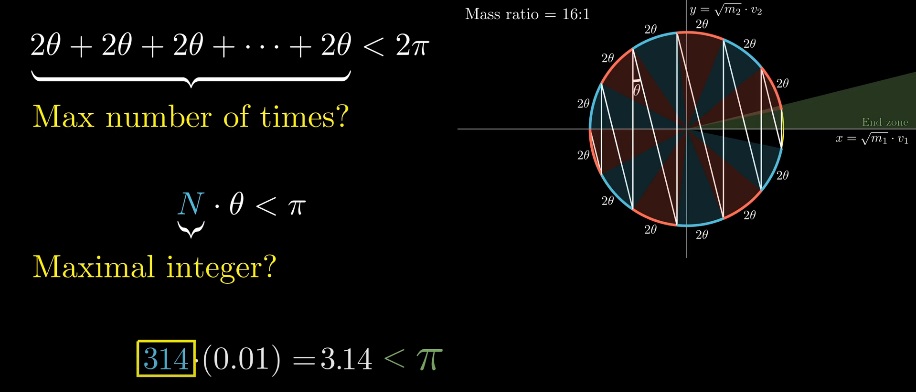
Всего длина окружности 2?, а длина дуги определяется половиной угла, который равен соотношению корней из масс блоков (чем больше разница — тем меньше угол). Порядок разницы масс будет определять «точность» ?: 3, 31, 314
Источники
- The Pi Machine: The most unexpected answer to a counting puzzle
- PLAYING POOL WITH ? (2003)
- Throwing ? at a wall (2006)
P.S.
еще конспект от 3Blue1Brown:
rahmaevao
Вообще удивляешься, как эти константы проникают везде и как они связаны со всем в мире. Я не только про ?, которое здесь с первого взгляда ни при чем. Но объяснение ставит все на место.
Alert1234
Числа ? и e входят в формулу Эйлера, которая связывает 5 самых главных констант — ноль, единицу, мнимую единицу i и, собственно, числа ? и е:
e^i? + 1 = 0
yurixi
Есть формула, которая не так популярна, но более интересна:
?e^(- ? x?) dx = 1
Если в первой формуле легко можно понять, что поворот на полкруга это разворот, то с чего бы в формуле c интегралом быть числу пи, сразу не догадаешься.
Ellarihan
А тут в чём соль? Вижу что при интегрировании от минус бесконечности до плюс бесконечности даёт 1, но глубинная суть интеграла как-то ускользает.
yurixi
Если Пи убрать, интеграл будет равен корню из Пи. Почему?
Если расширить интеграл на плоскость e^(-x^2-y^2), то интеграл будет равен Пи. Откуда? Когда считается интеграл по плоскости, он раскладывается на интеграл вдоль радиуса и интеграл по кругу, и вот отсюда Пи, из пределов интегрирования и возникает.
sebres
Вариация на тему Гауссовых интегралов...
Может тут понятнее станет (см. на площадь функции f(x)):
https://www.integral-calculator.ru/#expr=e%5E%28-%20%CF%80x%C2%B2%29&lbound=minf&ubound=inf
MetromDouble
Поэтому куда ни плюнь эти константы будут возникать
Цитата взята из этой статьи
lpssp
вернее будет сказать, что эти константы непосредственно связаны с нашими моделями окружающих явлений.
ss-nopol
Так как мы и «наши» модели возникли в этом мире и из этого мира, то вернее будет то, что наши модели непосредственно связаны с этими константами, которые отражают особенности нашего мира.
Эта гипотеза проверяема — достаточно связаться с инопланетянами из нашего мира и спросить, какие у них константы и модели. Если их математика окажется примерно такая же, то получается что «наши» модели не совсем наши.
MetromDouble
Ваш комментарий ничего не изменил и не уточнил. Во Вселенной нет ни одного, даже гипотетического, процесса, при котором термодинамические системы обмениваются информацией без взаимодействия или взаимодействуют без обмена информацией. А это значит, что ничего лучше приближённых к реальности моделей нам не видать, но при этом эти самые модели будут развиваться в одинаковом направлении и приводить к одинаковым выводам по всей Вселенной.
Эти константы никак не привязаны к нашим моделям, они естественные
lpssp
Нет, друг мой, эти константы не естественные, а являются следствием нашего моделирования окружающей действительности, просто по определению. Как известно наши модели являются приближенными и идеализированными. Пространство таки в реальности неоднородно и анизатропно, а то, что мы считаем по другому — это просто приближение работающее на больших масштабах, напрмер.
«А это значит, что ничего лучше приближённых к реальности моделей нам не видать» — а я где-то утверждал обратное? К чему это вообще было?
«Эти константы никак не привязаны к нашим моделям, они естественные.» — эти константы — следствие наших моделий и таким образом таки к ним приаязаны. Что значит естественные я не понял. Где во вселенной расположено число Пи, например?
P.S. А так то мой комментарий уточнил, что модель явления != явление.
Soffort
Мир даётся нам в ощущениях. А значит мы по-определёнию не способны воспринимать реальность напрямую, а не в виде упрощённых моделей. Следовательно, модель не обязана быть тождественной реальному объекту, процессу или системе, а лишь предоставлять достаточную для нашего восприятия точность.
lpssp
Совершенно согласен.
MetromDouble
До Теории Всего (или может чуть раньше неё) происхождение природных констант (не только Пи и е) и почему их значение именно такое, выяснить не удастся. Так что я по умолчанию слабее вас в аргументах в этом вопросе.
Это было к тому, что как-то странно уточнять про модели, когда любому человеку очевидно что мы всё на свете обрабатываем моделями. Спасибо, кэп.
Ну так и число Пи мы представляем приближенно и идеализированно, мы не можем посчитать бесконечное количество знаков после запятой.
Однако, в качестве аргумента я могу попробовать сказать, что модельное восприятие не относится к некоторым трансцендентным числам, которые возникают внезапно в самых разных моделях, как бы мы ни изворачивались, чтобы обойтись без них (либо изменить их значения). Можно сказать, что через них модели и реальность стыкуются.
Ну и не забывайте, в конце концов, что мозги, которыми мы придумываем модели, действуют в рамках всё тех же физических законов и не могут их нарушить, чтобы измыслить невозможные модели, действующие по невозможной логике.
Ещё ваш первый комментарий затрагивает не только физику, но и философию. Поэтому любые споры уйдут в плоскость вопросов «что такое реальность» и «что первично — мысль или материя». Я этого хотел бы избежать, поэтому завершу дискуссию.
Upd.: Может будет полезно — habr.com/ru/post/201452. Здесь представлены попытки определить пространства с иными числами Пи. Не особо удачные.
lpssp
Более того, совершенно не ясно возможно ли создать такую теорию всего или мы обречены на бесконечное уточнение. Вопрос очень спорный.
Ну, это демагогия какая-то. Уточнение было — было. Обобщения типо всем понятно или никому не ясно оставим для бульварных газет.
Вот только число Пи — это просто математическая константа, которая выводится из математических объектов, напрмер, а математика != физика. Там даже понятие дифференциала несколько отличается.
Ну вот это вообще не верно, я вам такую модель придумаю, что вы в ней логики вообще не найдете, собственно поиграйте в игры, там такого полно. А в рамках каких конкретно законов действует сознание, вообще не ясно.
Вот это точно.
vectorplus
А жаль. Меня как раз такие дискуссии интересуют.
rafuck
Это не совсем так. Математика является инструментом моделирования реальности. Это абстактаная наука. И именно в ней (в математике) возникают эти два иррациональных числа.
vectorplus
Модели должны обладать предсказательной силой, для этого они и нужны. Математика имеет это свойство. Пифагоровы штаны равны не только в абстракции, но и когда амбар строишь. Может, и число пи отлито в центре чёрной дыры из антиматерии, но мы просто не знаем.
yurixi
Как же интересно наблюдать, когда люди не различают, когда строят математику, а когда используют. С амбаром, кстати, различают — вот ведь парадокс!
Tyusha
Почитала. "Наука и жизнь" хоть и была относительно респектабельным журналом, но и там ерунды хватало. Статья так себе… Все притянуто за ушли, как минимум.
MetromDouble
Что именно притянуто за уши? Связь этих констант с пространственно-временными симметриями? Если так, то вы слишком круто берёте, хотелось бы услышать опровержение в твёрдых аргументах
alexxz
Ага, только вот в модели в статье используются законы сохранения энергии и импульса, а константа вылезает ? 8-\
ANIDEANI
а ещё pi может быть pi = 1
профи математики, расскажут. А если не расскажут, то не профи математики.
alexxz
Про единицу не знаю, но вот 4 — бывает: en.wikipedia.org/wiki/Taxicab_geometry
grub-itler
Пифагорейцы это отметили 2к тысяч лет назад. При этом некоторые утверждают, что 2+2=4 это чисто условное соглашение… Еслиб я был умный, яб прикинул что будет с константами если 2+2=3.