В задаче о надстроке по входному набору строк требуется найти кратчайшую строку, которая содержит каждую из них в качестве подстроки. Данная задача возникает в разных приложениях, например, в сборке генома или сжатии данных. Эта задача NP-трудная, поэтому рассчитывать на эффективный алгоритм поиска точного решения не приходится.
Максим Николаев — аспирант ПОМИ РАН, преподаватель Computer Science Center и СПбГУ, учитель математики в лицее №533 в Санкт-Петербурге. В 2019 году он окончил CS центр по направлению Современная информатика. В статье ниже Максим рассказывает о своей исследовательской работе во время обучения по поиску приближенных решений задачи о надстроке.

Как и в других NP-трудных задачах, в задаче о надстроке представляют интерес и активно изучаются приближенные алгоритмы, которые достаточно быстро находят достаточно точное решение. Наилучший известный на сегодняшний день полиномиальный алгоритм находит надстроку не более, чем в раза более длинную, чем точное решение.
В то же время уже более 30 лет остается нерешённой так называемая жадная гипотеза, которая утверждает, что элементарный жадный алгоритм «выбери две строки с максимальным пересечением и слей их; продолжай так делать, пока не останется одна строка» является 2-приближенным.
Более подробно о задаче и возникающих в ней гипотезах можно узнать в замечательной открытой лекции CS центра. Далее будет изложена краткая выжимка из неё и описание моих результатов.
В попытке подобраться к решению жадной гипотезы и к разработке более качественных приближенных алгоритмов группой Александра Куликова был разработан теоретико-графовый подход, который позволяет в удобной форме изучать структуру пересечений исходных строк друг с другом. Для этого вводится так называемый иерархический граф, в котором вершинами являются исходные строки и всевозможные их подстроки, а ориентированные ребра идут из префикса каждой строки в эту строку и из строки в ее суффикс. Под префиксом и суффиксом строки понимаются строки, которые получаются при выкидывании последней и первой её буквы соответственно. Вершины графа удобно расположить по уровням в зависимости от длины соответствующих строк, поэтому граф и называется иерархическим. На рисунке ниже показан иерархический граф для исходного набора строк {aaa, cae, aec, eee}, которые изображаются в прямоугольниках. Пустая строка обозначается через .

Где же здесь надстроки? Надстрокам в этом графе соответствуют циклы, проходящие через и все исходные вершины. По каждому такому циклу можно восстановить надстроку, и наоборот. Например, на рисунке ниже отмечен цикл, соответствующей надстроке aaaecaeee. В этой надстроке исходные строки встречаются в порядке aaa aec cae eee, и именно в таком порядке их обходит упомянутый цикл.
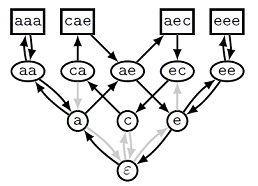
Нетрудно показать, что длина надстроки всегда равна количеству идущих вверх стрелок в соответствующем цикле (в примере их 9). Это значит, что задача поиска кратчайшей надстроки превращается в задачу поиска кратчайшего цикла в иерархическом графе.
Естественно, такая замечательная структура как иерархический граф так и просит, чтобы на её основе разработали интересные алгоритмы. Моя задача состояла в изучении двух таких алгоритмов.
Первый из них, Greedy Hierarchical Algorithm (GHA), является, по-видимому, самым простым способом построить цикл, проходящий через исходные вершины и который бы мог претендовать на хорошее приближение точного решения. Как следует из названия, он является жадным и кратко может быть описан так: пройдем по уровням графа сверху вниз, а внутри уровня по всем вершинам в лексикографическом порядке; для каждой из вершин, во-первых, обеспечим равную входящую и исходящую степень (чтобы решение было циклом) за счет добавления подходящего количества ребер между текущим уровнем и более низким, а во-вторых, если вершина является исходной или если она является последней в лексикографическом порядке вершиной некоторой уже построенной циклической компоненты (ребра которой лежат выше данного уровня), то мы выпускаем из неё два ребра в её префикс и суффикс. Работа алгоритма для нашего датасета из предыдущих примеров отражена на рисунке ниже. Нетрудно видеть, что на второй картинке ребра из aa и ee были выпущены, чтобы обеспечить связь исходных строк aaa и eee с , а ребра из ca и ec — чтобы сбалансировать соответствующие вершины.

Видно, что алгоритм старается добавлять как можно меньше ребер — он делает это только для обеспечения цикличности и связности — необходимых условий для того, чтобы цикл соответствовал некоторой надстроке.
Второй алгоритм в некотором смысле противоположен первому. Он называется Collapsing Algorithm (CA), и если GHA стартует с пустого графа и добавляет ребра только в случае необходимости, то CA стартует с некоторого решения и пытается убрать из него лишние ребра. Убирание лишних ребер происходит следующим образом: алгоритм движется по графу сверху вниз, на каждом уровне обходя вершины в лексикографическом порядке; если для некоторой вершины в цикле имеется «галка» , то алгоритм старается её «обвалить» (поэтому и Collapsing), заменив её на «галку» , но только если это не нарушит связность цикла. Если же находится на первом уровне, то эта галка просто удаляется. Таким образом алгоритм старается сбросить все лишние пары ребер вниз, после чего удалить. Пример работы CA на удвоенном оптимальном решении (удвоенность нужна, чтобы были лишние ребра) можно увидеть на рисунке ниже.

Моей задачей было исследование описанных алгоритмов с прицелом на доказательство или опровержение какой-нибудь из гипотез, описанных ниже.
Гипотеза Collapsing Conjecture — возьмите любое решение, удвойте в нем ребра и подайте на вход CA. Полученный результат не зависит от изначального решения!
Если эта гипотеза верна, то у нас появляется очень простой 2-приближенный алгоритм: возьмите любое решение (например, тривиальное, которое получается конкатенацией всех исходных строк), удвойте в нем ребра и обвалите. В итоге получится то же самое, как если бы вы удвоили и обвалили оптимальное решение. Но если так, то полученный результат не более чем в два раза длиннее оптимального.
Гипотеза Greedy Hierarchical Conjecture — граф, получающийся после обвала любого удвоенного решения, это в точности граф, который строит GHA!
Данная гипотеза была проверена на очень большом количестве случайных и неслучайных наборов исходных строк, но контрпример найти так и не удалось. В частности, для приведенных выше примеров, иллюстрирующих работу GHA и CA, гипотеза верна. Из этой гипотезы сразу следует, что GHA является 2-приближенным.
Гипотеза Weak Greedy Hierarchical Conjecture — GHA является 2-приближенным.
Даже если предыдущие две гипотезы неверны, то GHA все равно может быть 2-приближенным.
Первое, что меня заинтересовало: как связан GHA с обычным жадным алгоритмом? На некоторых примерах GHA строит более короткое решение, но всегда ли это происходит? Можем ли мы показать, что GHA не хуже жадного? Как в терминах иерархического графа описать жадный алгоритм? Как в иерархическом графе увидеть момент «склейки» двух строк в одну?
В процессе работы над всеми этими вопросами я выяснил, что GHA на самом деле является частным случаем обычного жадного алгоритма! Дело в том, что жадный алгоритм является недетерминированным: в его описании не оговаривается, что происходит, если есть несколько пар строк с максимальным пересечением. Предполагается, что алгоритм может выбрать произвольную пару, а значит, вообще говоря, даже на одном и том же датасете он может выдавать различные решения. GHA по своей сути является некоторой детерминацией алгоритма — в его определении заложено, в каком именно порядке будут объединяться пары строк, таким образом по данному набору исходных строк всегда строится одно и то же решение. Данное свойство означает, что из жадной гипотезы следует 2-приближенность GHA, поэтому, строго говоря, доказать Weak Greedy Hierarchical Conjecture должно быть проще, чем жадную гипотезу.
Также оказалось, что эта детерминация не лучше исходного алгоритма — существуют примеры, на которых GHA работает хуже, чем некоторая другая детерминация жадного.
Следующий этап моего исследования был посвящен более подробному изучению работы GHA на датасете, в котором длина всех строк ограничена некоторой константой. Если эта константа 2, то GHA является точным, а сама задача, стало быть, из класса P, а начиная с максимальной длины 3 задача становится NP-полной и для этого случая уже было неясно, насколько приближенным является GHA.
Для случая строк длины не больше 3 я показал, что GHA является 1.5-приближенным и эта оценка является асимптотически точной, т. е. для любого можно привести датасет, на котором GHA построит решение в раз более длинное, чем точное.
К сожалению, для случая строк длины 4 или более ничего придумать не удалось, и я решил переключиться на исследование остальных гипотез.
Во-первых, после работы над строками длины не больше 3 я решил попробовать разобраться с Greedy Hierarchical Conjecture для этого случая, и мне это удалось. Причем был доказан даже более сильный результат: для того, чтобы все обвалилось, в GHA не нужно удваивать всё решение — достаточно добавить к решению произвольное покрытие исходных вершин циклами (которые уже не обязаны образовывать один связный цикл).
Во-вторых, я выяснил, что если в общем случае к решению, полученному GHA, приклеить произвольный набор циклов (к примеру, подходит само решение GHA), а потом все обвалить, то снова получится GHA. Это означает, что из Collapsing Conjecture следует Greedy Hierarchical Conjecture. Так как обратное следствие очевидно, то выходит, что эти две гипотезы равносильны.
Все полученные результаты, кроме 1.5-приближенности, были включены в статью Collapsing Superstring Conjecture, которая была принята на конференцию APPROX 2019 и опубликована в ее трудах. Эта одна из ведущих конференций по приближенным алгоритмам, что свидетельствует об актуальности темы и интересе к ней у научного сообщества, несмотря на то, что ни одна из гипотез доказана или опровергнута не была.
После выпуска из центра я все еще периодически возвращаюсь к этой задаче. Ни по какой из гипотез на момент осени 2020 так ничего определенного не известно, но всё равно появляется более глубокое понимание проблем, которые препятствуют их решению. В случае, если эта задача покажется интересной, можно обращаться к Александру Куликову за актуальной информацией и подробными комментариями.
Максим Николаев — аспирант ПОМИ РАН, преподаватель Computer Science Center и СПбГУ, учитель математики в лицее №533 в Санкт-Петербурге. В 2019 году он окончил CS центр по направлению Современная информатика. В статье ниже Максим рассказывает о своей исследовательской работе во время обучения по поиску приближенных решений задачи о надстроке.

Жадная гипотеза
Как и в других NP-трудных задачах, в задаче о надстроке представляют интерес и активно изучаются приближенные алгоритмы, которые достаточно быстро находят достаточно точное решение. Наилучший известный на сегодняшний день полиномиальный алгоритм находит надстроку не более, чем в раза более длинную, чем точное решение.
В то же время уже более 30 лет остается нерешённой так называемая жадная гипотеза, которая утверждает, что элементарный жадный алгоритм «выбери две строки с максимальным пересечением и слей их; продолжай так делать, пока не останется одна строка» является 2-приближенным.
Более подробно о задаче и возникающих в ней гипотезах можно узнать в замечательной открытой лекции CS центра. Далее будет изложена краткая выжимка из неё и описание моих результатов.
Иерархический граф и надстроки
В попытке подобраться к решению жадной гипотезы и к разработке более качественных приближенных алгоритмов группой Александра Куликова был разработан теоретико-графовый подход, который позволяет в удобной форме изучать структуру пересечений исходных строк друг с другом. Для этого вводится так называемый иерархический граф, в котором вершинами являются исходные строки и всевозможные их подстроки, а ориентированные ребра идут из префикса каждой строки в эту строку и из строки в ее суффикс. Под префиксом и суффиксом строки понимаются строки, которые получаются при выкидывании последней и первой её буквы соответственно. Вершины графа удобно расположить по уровням в зависимости от длины соответствующих строк, поэтому граф и называется иерархическим. На рисунке ниже показан иерархический граф для исходного набора строк {aaa, cae, aec, eee}, которые изображаются в прямоугольниках. Пустая строка обозначается через .

Где же здесь надстроки? Надстрокам в этом графе соответствуют циклы, проходящие через и все исходные вершины. По каждому такому циклу можно восстановить надстроку, и наоборот. Например, на рисунке ниже отмечен цикл, соответствующей надстроке aaaecaeee. В этой надстроке исходные строки встречаются в порядке aaa aec cae eee, и именно в таком порядке их обходит упомянутый цикл.

Нетрудно показать, что длина надстроки всегда равна количеству идущих вверх стрелок в соответствующем цикле (в примере их 9). Это значит, что задача поиска кратчайшей надстроки превращается в задачу поиска кратчайшего цикла в иерархическом графе.
Greedy Hierarchical Algorithm и Collapsing Algorithm
Естественно, такая замечательная структура как иерархический граф так и просит, чтобы на её основе разработали интересные алгоритмы. Моя задача состояла в изучении двух таких алгоритмов.
Первый из них, Greedy Hierarchical Algorithm (GHA), является, по-видимому, самым простым способом построить цикл, проходящий через исходные вершины и который бы мог претендовать на хорошее приближение точного решения. Как следует из названия, он является жадным и кратко может быть описан так: пройдем по уровням графа сверху вниз, а внутри уровня по всем вершинам в лексикографическом порядке; для каждой из вершин, во-первых, обеспечим равную входящую и исходящую степень (чтобы решение было циклом) за счет добавления подходящего количества ребер между текущим уровнем и более низким, а во-вторых, если вершина является исходной или если она является последней в лексикографическом порядке вершиной некоторой уже построенной циклической компоненты (ребра которой лежат выше данного уровня), то мы выпускаем из неё два ребра в её префикс и суффикс. Работа алгоритма для нашего датасета из предыдущих примеров отражена на рисунке ниже. Нетрудно видеть, что на второй картинке ребра из aa и ee были выпущены, чтобы обеспечить связь исходных строк aaa и eee с , а ребра из ca и ec — чтобы сбалансировать соответствующие вершины.

Видно, что алгоритм старается добавлять как можно меньше ребер — он делает это только для обеспечения цикличности и связности — необходимых условий для того, чтобы цикл соответствовал некоторой надстроке.
Второй алгоритм в некотором смысле противоположен первому. Он называется Collapsing Algorithm (CA), и если GHA стартует с пустого графа и добавляет ребра только в случае необходимости, то CA стартует с некоторого решения и пытается убрать из него лишние ребра. Убирание лишних ребер происходит следующим образом: алгоритм движется по графу сверху вниз, на каждом уровне обходя вершины в лексикографическом порядке; если для некоторой вершины в цикле имеется «галка» , то алгоритм старается её «обвалить» (поэтому и Collapsing), заменив её на «галку» , но только если это не нарушит связность цикла. Если же находится на первом уровне, то эта галка просто удаляется. Таким образом алгоритм старается сбросить все лишние пары ребер вниз, после чего удалить. Пример работы CA на удвоенном оптимальном решении (удвоенность нужна, чтобы были лишние ребра) можно увидеть на рисунке ниже.

Разные гипотезы
Моей задачей было исследование описанных алгоритмов с прицелом на доказательство или опровержение какой-нибудь из гипотез, описанных ниже.
Гипотеза Collapsing Conjecture — возьмите любое решение, удвойте в нем ребра и подайте на вход CA. Полученный результат не зависит от изначального решения!
Если эта гипотеза верна, то у нас появляется очень простой 2-приближенный алгоритм: возьмите любое решение (например, тривиальное, которое получается конкатенацией всех исходных строк), удвойте в нем ребра и обвалите. В итоге получится то же самое, как если бы вы удвоили и обвалили оптимальное решение. Но если так, то полученный результат не более чем в два раза длиннее оптимального.
Гипотеза Greedy Hierarchical Conjecture — граф, получающийся после обвала любого удвоенного решения, это в точности граф, который строит GHA!
Данная гипотеза была проверена на очень большом количестве случайных и неслучайных наборов исходных строк, но контрпример найти так и не удалось. В частности, для приведенных выше примеров, иллюстрирующих работу GHA и CA, гипотеза верна. Из этой гипотезы сразу следует, что GHA является 2-приближенным.
Гипотеза Weak Greedy Hierarchical Conjecture — GHA является 2-приближенным.
Даже если предыдущие две гипотезы неверны, то GHA все равно может быть 2-приближенным.
Моя работа
Первое, что меня заинтересовало: как связан GHA с обычным жадным алгоритмом? На некоторых примерах GHA строит более короткое решение, но всегда ли это происходит? Можем ли мы показать, что GHA не хуже жадного? Как в терминах иерархического графа описать жадный алгоритм? Как в иерархическом графе увидеть момент «склейки» двух строк в одну?
В процессе работы над всеми этими вопросами я выяснил, что GHA на самом деле является частным случаем обычного жадного алгоритма! Дело в том, что жадный алгоритм является недетерминированным: в его описании не оговаривается, что происходит, если есть несколько пар строк с максимальным пересечением. Предполагается, что алгоритм может выбрать произвольную пару, а значит, вообще говоря, даже на одном и том же датасете он может выдавать различные решения. GHA по своей сути является некоторой детерминацией алгоритма — в его определении заложено, в каком именно порядке будут объединяться пары строк, таким образом по данному набору исходных строк всегда строится одно и то же решение. Данное свойство означает, что из жадной гипотезы следует 2-приближенность GHA, поэтому, строго говоря, доказать Weak Greedy Hierarchical Conjecture должно быть проще, чем жадную гипотезу.
Также оказалось, что эта детерминация не лучше исходного алгоритма — существуют примеры, на которых GHA работает хуже, чем некоторая другая детерминация жадного.
Следующий этап моего исследования был посвящен более подробному изучению работы GHA на датасете, в котором длина всех строк ограничена некоторой константой. Если эта константа 2, то GHA является точным, а сама задача, стало быть, из класса P, а начиная с максимальной длины 3 задача становится NP-полной и для этого случая уже было неясно, насколько приближенным является GHA.
Для случая строк длины не больше 3 я показал, что GHA является 1.5-приближенным и эта оценка является асимптотически точной, т. е. для любого можно привести датасет, на котором GHA построит решение в раз более длинное, чем точное.
К сожалению, для случая строк длины 4 или более ничего придумать не удалось, и я решил переключиться на исследование остальных гипотез.
Во-первых, после работы над строками длины не больше 3 я решил попробовать разобраться с Greedy Hierarchical Conjecture для этого случая, и мне это удалось. Причем был доказан даже более сильный результат: для того, чтобы все обвалилось, в GHA не нужно удваивать всё решение — достаточно добавить к решению произвольное покрытие исходных вершин циклами (которые уже не обязаны образовывать один связный цикл).
Во-вторых, я выяснил, что если в общем случае к решению, полученному GHA, приклеить произвольный набор циклов (к примеру, подходит само решение GHA), а потом все обвалить, то снова получится GHA. Это означает, что из Collapsing Conjecture следует Greedy Hierarchical Conjecture. Так как обратное следствие очевидно, то выходит, что эти две гипотезы равносильны.
Конференция APPROX 2019
Все полученные результаты, кроме 1.5-приближенности, были включены в статью Collapsing Superstring Conjecture, которая была принята на конференцию APPROX 2019 и опубликована в ее трудах. Эта одна из ведущих конференций по приближенным алгоритмам, что свидетельствует об актуальности темы и интересе к ней у научного сообщества, несмотря на то, что ни одна из гипотез доказана или опровергнута не была.
Дальнейшая работа
После выпуска из центра я все еще периодически возвращаюсь к этой задаче. Ни по какой из гипотез на момент осени 2020 так ничего определенного не известно, но всё равно появляется более глубокое понимание проблем, которые препятствуют их решению. В случае, если эта задача покажется интересной, можно обращаться к Александру Куликову за актуальной информацией и подробными комментариями.

