Введение
Криптографическая хэш функция представляет собой набор шагов, позволяющих преобразовать произвольный блок данных в последовательность фиксированной длины. Любое изменение входных данных ведёт к изменению значения функции. Хэш функции используются для вычисления контрольных сумм, при выработке электронной подписи, при сохранении паролей в системах защиты в виде хеш-кода и т.д.
В качестве нового стандарта SHA-3 в конкурсе хэш-функций, проводимых Национальным институтом стандартов и технологий(NIST) в 2009 году было предложено семейство хеш-функций CubeHash.
В данной статье описывается принцип работы данного семейства, а также обсуждается устойчивость алгоритма к различным атакам.
Описание алгоритма
Далее приводится алгоритм работы ![]() согласно спецификации [1].
согласно спецификации [1].
Работа алгоритма определяется 3 параметрами:
 - размер выходной последовательности в битах,
- размер выходной последовательности в битах, 
 - количество раундов,
- количество раундов, 
 - размер блоков входного сообщения в байтах,
- размер блоков входного сообщения в байтах, 
Идея алгоритма заключается в последовательном преобразовании ![]() состояния на основе входной последовательности. Алгоритм состоит из 5 шагов:
состояния на основе входной последовательности. Алгоритм состоит из 5 шагов:
инициализация внутреннего состояния
разбиение сообщения на блоки
итеративное преобразование состояния
завершающее преобразование состояния
вывод результата
Рассмотрим каждый шаг подробнее.
Инициализация
Внтуреннее состояние алгоритма представляет собой набор из 32 четырёх-байтовых слов ![]() (представлены в little-endian).
(представлены в little-endian).
Первые 3 слова ![]() инициализируются значениями
инициализируются значениями ![]() . Остальные слова инициализируются нулями. Далее к внутреннему состоянию
. Остальные слова инициализируются нулями. Далее к внутреннему состоянию ![]() раз применяются функция преобразования
раз применяются функция преобразования![]() .
.
Разбиение на блоки
Входное сообщение дополняется единичным битом. Затем дополняется нулевыми битами до длины кратной ![]() . При этом нет необходимости использовать дополнительный буффер для хранения добавленных битов. Достаточно лишь отслеживать число обработанных битов в текущем блоке.
. При этом нет необходимости использовать дополнительный буффер для хранения добавленных битов. Достаточно лишь отслеживать число обработанных битов в текущем блоке.
Преобразование состояния
После инициализации блоки входного сообщения обрабатываются последовательно. Первым ![]() байтам внутреннего состояния присваиваетется результат исключающего или с текущим блоком сообщения длины
байтам внутреннего состояния присваиваетется результат исключающего или с текущим блоком сообщения длины ![]() . Затем ко внутреннему состоянию
. Затем ко внутреннему состоянию ![]() применяется функция
применяется функция ![]() .
.
Завершающее преобразование
После обработки всех блоков к последнему слову ![]() применяется исключающее или с 1, после чего к состоянию
применяется исключающее или с 1, после чего к состоянию![]() применяется функция
применяется функция ![]() .
.
Вывод результат
После заверщающего преобразования в качестве результата работы алгоритма выводятся первые ![]() битов внутреннего состояния.
битов внутреннего состояния.
Функция преобразования F
Фунцкия ![]() представляет собой набор элементарных битовых операций, таких как сложение по модулю, исключающее или, и перестановка слов. В итоге функция
представляет собой набор элементарных битовых операций, таких как сложение по модулю, исключающее или, и перестановка слов. В итоге функция ![]() из 10 шагов:
из 10 шагов:
прибавить
 к
к  для
для 
выполнить сдвиг
 на семь битов влево, для
на семь битов влево, для 
выполнить перестановку
 и
и 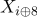 , для
, для 
присвоить
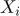 значение
значение  , для
, для 
выполнить перестановку
 и
и  , для
, для 
повторить шаг 1
выполнить сдвиг
 на одиннадцать битов влево, для
на одиннадцать битов влево, для 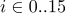
выполнить перестановку
 и
и 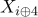 , для
, для 
повторить шаг 4
выполнить перестановку
 и
и  , для
, для 
Схематично работу функции ![]() можно изобразить следующим образом [2]:
можно изобразить следующим образом [2]:

Стойкость хэш-функции
Любая криптографическая функция должа быть устойчива к следующим типам атак:
Атака нахождения прообраза: по заданному значению хэш-функции найти сообщение с данным хэшом.
Коллизионная атака: найти 2 различных сообщения с одинаковы значением хэша.
Не существет хэш-функций, которые позволяют полностью защититься от данных видов атак, однако если хэш-функция устроена таким образом, чтобы сделать атаку практически невозможной с использованием современных вычислительных устройств, то говорят, что функция устойчива.
Стойкость CubeHash
Коллизионная атака
После обрабоки сообщения, результат обработки и само сообщение добавляются в таблицу соответствий. Т.к. существует конечное число значений хэша, а число возможных сообщений гораздо больше, то коллизии обязаны существовать.
Данный подход позволяет найти совпадения с вероятностью 50% за порядка ![]() операций. Также требуется хранить в памяти сообщения и соответсвующие им значения хэша. Следует отметить, что подобные вычисления невозможны на современных устройствах для размера хэшей 128 и более [3].
операций. Также требуется хранить в памяти сообщения и соответсвующие им значения хэша. Следует отметить, что подобные вычисления невозможны на современных устройствах для размера хэшей 128 и более [3].
Атака нахождения прообраза
Входные сообщения обрабатываются последовательно. Результаты работы функции сравниваются с целевым значением хэша. Если результат хэширования совпадает с требуемым значением, то атака считается успешной. Данная процедура позволяет найти прообраз за вермя порядка ![]() . Следует отметить, что подобные вычисления невозможны на современных устройствах для размера хэшей 64 и более[3].
. Следует отметить, что подобные вычисления невозможны на современных устройствах для размера хэшей 64 и более[3].
Далее будут приведены методы взлома ![]() на особенностях устройства алгоритма.
на особенностях устройства алгоритма.
Взлом с использованием одного блока
Авторы [4] предложили метод для взлома алгоритма основанный на том, что значение хэша зависит только от первых ![]() бит конечного сотояния, а изменение остальной части
бит конечного сотояния, а изменение остальной части ![]() никак не влияет на результат.
никак не влияет на результат.
В начале по тройке ![]() вычислияется начальное состояние
вычислияется начальное состояние ![]() . Затем для некоторого произвольного
. Затем для некоторого произвольного ![]() выполняется серия обратных преобразований(вплоть до операции исключающего или с первым блоком сообщения), ведущая к состоянию
выполняется серия обратных преобразований(вплоть до операции исключающего или с первым блоком сообщения), ведущая к состоянию ![]() . Если у
. Если у ![]() последних
последних ![]() байта совпадают с последними
байта совпадают с последними ![]() байтами
байтами ![]() , то применяя операцию исключающего или между первыми
, то применяя операцию исключающего или между первыми ![]() байтами
байтами ![]() и
и ![]() , получаем требуемый прообраз.
, получаем требуемый прообраз.
Следует отметить, что хотя эта атака находит прообраз за меньшее время, чем поиск грубой силы, это возможно только при чрезвычайно больших значениях ![]() . Анализ показывает, что число попыток для взлома растёт
. Анализ показывает, что число попыток для взлома растёт ![]() , поэтому взлом возможен только при больших значениях
, поэтому взлом возможен только при больших значениях ![]() , находящихся вне диапазона рекомендуемых значений [2]. Кроме того, время, необходимое для выполнения этой атаки, линейно растет с увеличением
, находящихся вне диапазона рекомендуемых значений [2]. Кроме того, время, необходимое для выполнения этой атаки, линейно растет с увеличением ![]() .
.
Атака на основе симметрии функции F
Данная атака основа на свойстве функции ![]() сохранять симметрии своего 128-байтного состояния [2]. Всего существует 15 классов симметрии
сохранять симметрии своего 128-байтного состояния [2]. Всего существует 15 классов симметрии ![]() :
:
| AABBCCDD | EEFFGGHH | IIJJKKLL | MMNNOOPP |
| ABABCDCD | EFEFGHGH | IJIJKLKL | MNMNOPOP |
| ABBACDDC | EFFEGHHG | IJJIKLLK | MNNMOPPO |
| ABCDABCD | EFGHEFGH | IJKLIJKL | MNOPMNOP |
| ABCDBADC | EFGHFEHG | IJKLJILK | MNOPNMPO |
| ABCDCDAB | EFGHGHEF | IJKLKLIJ | MNOPOPMN |
| ABCDDCBA | EFGHHGFE | IJKLLKJI | MNOPPONM |
| ABCDEFGH | ABCDEFGH | IJKLMNOP | IJKLMNOP |
| ABCDEFGH | BADCFEHG | IJKLMNOP | JILKNMPO |
| ABCDEFGH | CDABGHEF | IJKLMNOP | KLIJOPMN |
| ABCDEFGH | DCBAHGFE | IJKLMNOP | LKJIPONM |
| ABCDEFGH | EFGHABCD | IJKLMNOP | MNOPIJKL |
| ABCDEFGH | FEHGBADC | IJKLMNOP | NMPOJILK |
| ABCDEFGH | GHEFCDAB | IJKLMNOP | OPMNKLIJ |
| ABCDEFGH | HGFEDCBA | IJKLMNOP | PONMLKJI |
Каждая буква буква представляет собой 32-битное слово. Повторяющееся буквы обозначают одинаковые слова. Для каждого из этих классов симметрии, функция ![]() не меняет структуры состояния, возможна лишь замена значений слов, с сохранением общей структуры. Кроме того, допустима композиция классов.
не меняет структуры состояния, возможна лишь замена значений слов, с сохранением общей структуры. Кроме того, допустима композиция классов.
Атака позволяет найти коллизии следующим способом.
получить симметричное состояние любого класса при прямом проходе
получить симметричное состояние любого класса при обратном проходе (необязательно данного класса)
для обоих состояний обрабатывать сообщения из одних только нулей, пока они не окажутся в одном классе симметрии
обрабатывать в обоих направлениях нулевые сообщения пока не встретятся одинаковые классы симметрии.
в обоих направлениях обрабатывать блоки сообщения, пока не встретятся коллизии
Анализ метода показывает, что можно получить коллизии за порядка операций. Что делает атаку невозможной для современных вычислительных устройств. Также длина соообщений оказывается больше
байт.
Производительность
Производительность криптографического програмного обеспечения в циклах на байт (cycle per byte или cpb). Данная единица обозначает число тактов процессора, необходимое для обработки 1 байта входной последовательности.
Сравнение производительности SHA-256, SHA-512 и CubeHash16/32 на процессорах Intel Core 2Duo 6f6 (a) и Intel Core 2 Duo E8400 1067a (b) [5]:
11.47 cpb: CubeHash 16/32, (b), amd64 architecture.
12.60 cpb: SHA-512, (b), amd64 architecture.
12.60 cpb: SHA-512, (a), amd64 architecture.
12.66 cpb: CubeHash 16/32, (a), amd64 architecture.
12.74 cpb: CubeHash 16/32, (b), x86 architecture.
14.07 cpb: CubeHash 16/32, (a), x86 architecture.
15.43 cpb: SHA-256, (b) x86 architecture.
15.53 cpb: SHA-256, (b), amd64 architecture.
15.56 cpb: SHA-256, (a), amd64 architecture
17.76 cpb: SHA-512, (b), x86 architecture.
20.00 cpb: SHA-512, (a), x86 architecture
22.76 cpb: SHA-256, (a), x86 architecture
Применение
Алгоритм CubeHash был предложен в качестве нового сдандарта для SHA-3 на конкурсе хэш-функций, проводимом NIST. Cubehash прошла во второй тур конкурса, однако так и не попала в пятёрку финалистов. Согласно авторам, CubeHash практически не уступает своим оппонентам в производительности, обеспечивая достаточный уровень защиты.
Стойкость метода увеличивается при уменьшении размера блока ![]() и при увеличении числа раундов
и при увеличении числа раундов ![]() . Таким образом, CubeHash 8 / 1-512 безопаснее CubeHash 1 / 1-512, а CubeHash 1 / 1-512 безопаснее, чем CubeHash 1 / 2-512. Самая слабая версия этого алгоритма - CubeHash 1/128- h.
. Таким образом, CubeHash 8 / 1-512 безопаснее CubeHash 1 / 1-512, а CubeHash 1 / 1-512 безопаснее, чем CubeHash 1 / 2-512. Самая слабая версия этого алгоритма - CubeHash 1/128- h.
Однако вычисление более стойких версий требует больше ресурсов: количество операций прямо пропорционально числу раундов ![]() и обратно пропорционально размеру блока
и обратно пропорционально размеру блока ![]() .
.
Источники
D. J. Bernstein. Cubehash specification (2.b.1)
Vikash Jha. Cryptanalysis of Cubehash.
Philip Doughty Jr. A Generic attack on CubeHash, a SHA-3 candidate.
Benjamin Bloom and Alan Kaminsky. Single Block Attacks and Statis-tical Tests on CubeHash.
D. J. Bernstein. CubeHash parameter tweak: 16 times faster.


centralhardware
А можно все таки использовать latex для математики? Я понимаю, то что на белой теме картинки выглядит очень похоже с рендером latex в html, но у нас на дворе 2020 год и хочется не смотреть на кучку картинок, просто потому, что у тебя темная тема, это ещё не затрагиваея людей с мониторами ультра высокого разрешения — они вас точно за картинки (которые никак не маштабируются, тут кстати можно вспомнить про людей с плохим зрением, которые обречены на достаапние лупы) не поблагодарят
centralhardware
У меня не то, чтобы дорогой телефон однако в представленых формулах отчётливо вижу мыло, человек с последним Айфоном, я подозреваю испытает флеш бек из 2010
centralhardware
Все это последнее: ну индекс то нижний можно было без картинки сделать
StanislavShimovolos Автор
В начале так и было, но почему-то после отправки на модерацию часть формул слетает.