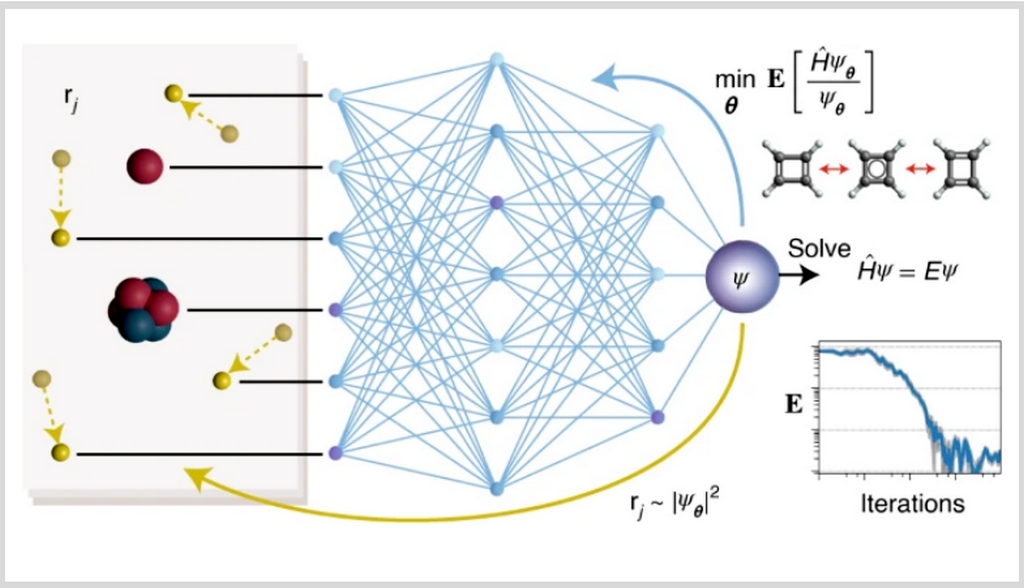
Группа ученых из Freie Universitat в Берлине разработала метод на основе искусственного интеллекта для вычисления основного состояния уравнения Шредингера в квантовой химии.

Данное научное направление занимается предсказанием химических и физических свойств молекул, основываясь исключительно на расположении их атомов в пространстве, без ресурсоемких и трудоемких лабораторных экспериментов. Решение уравнения Шредингера может значительно упростить задачу предсказания. Однако до сих пор было невозможно найти точное его решение для произвольных молекул.

В уравнении Шредингера рассматривается волновая функция, которая определяет поведение электронов в молекуле. Волновая функция отражает общее состояние, а не влияние отдельных электронов друг на друга. В связи с этим многие методы квантовой химии фактически отказываются от выражения волновой функции, пытаясь определить только энергию заданной молекулы. Однако вычисление приблизительных значений сказывается на качестве предсказания.

Другие методы представляют волновую функцию как массивный математический блок, но это сложно, поэтому метод можно применить на практике не более чем для нескольких атомов.

Команда Freie Universitat разработала метод глубокого обучения, который, как утверждают исследователи, позволяет достичь точности и вычислительной эффективности.

Глубокая нейронная сеть служит для представления волновых функций электронов. Она изучает сложные модели расположения электронов вокруг ядер. «Особенностью электронных волновых функций является их антисимметрия. Когда происходит обмен двумя электронами, волновая функция должна менять знак. Нам пришлось встроить это свойство в архитектуру нейронной сети, чтобы подход заработал», — отмечают авторы разработки.

Эта особенность известна как принцип исключения Паули, поэтому авторы назвали свой метод «PauliNet». Помимо принципа исключения Паули, электронные волновые функции также обладают другими фундаментальными физическими свойствами, и PauliNet интегрирует эти свойства в глубокую нейронную сеть.

Однако и у нового метода нашлись недостатки. Во-первых, отмечается, что он не вариационный. В работе системы на ИИ, в отличие от методов квантовой химии, невозможно увеличить количество степеней свободы для получения более точного результата. Во-вторых, пока нет четкого способа улучшить данный метод, так как в него уже заложили все фундаментальные данные.

См. также:

• «Расставляя все точки над «пси»»
• «Квантовая теория. Вселенная из волн вероятностей»
• «Путь частицы или волна-пилот наносит ответный удар»