
Привет, Хабр!
Новая статья цикла о моделировании в задачах управления кредитным риском (предыдущие статьи смотрите здесь и здесь) посвящена EAD — компоненте, отражающей размер задолженности заемщика перед банком в момент дефолта.
Как спрогнозировать сумму кредитного требования в момент дефолта, при условии, что момент дефолта неизвестен, и вообще может не настать? Как поступать с экстремальными, особенно большими по абсолютному значению, EAD? А если кредитный продукт, по которому нужно оценить риск — это так называемый револьверный кредит, где нет установленных регулярных платежей,- как, например, кредитка с кредитным лимитом?
Эти и подобные им вопросы возникают при моделировании компоненты. Их и рассмотрим под катом.
EAD как одна из компонент EL
Общая формула ожидаемых потерь (Expected Loss, EL) выглядит так[1]:

— вероятность дефолта;
— это кредитные обязательства по договору на момент дефолта. Кредитные обязательства, сумма кредитного требования, балансовая часть долга, баланс — это синонимы для описания суммы средств, которые заемщик должен банку. Соответственно, EAD — сумма средств, которые заемщик должен банку в момент дефолта.
— доля EAD, которую заемщик не возместит банку в течение условленного времени после дефолта.
В публикациях и на проектах, посвященных оценке ожидаемых потерь, основное внимание приковано к моделированию и оценке PD. И если LGD также удается уделить время, особенно в части сбора целевого события и выбора архитектуры решения, то на EAD его практически не остаётся.
Одна из причин в том, что основные «кнопки» управления итоговым значением EL расположены именно в компонентах PD и LGD: калибровка, горизонт наблюдения и сбора восстановления и др.
Тем не менее EAD является важным параметром, поскольку
Наша цель — дать быструю инструкцию, которая учтет основные требования и позволит собрать baseline для решения задачи.
Методы оценки EAD
Подходы к оценке EAD различаются в зависимости от типа договора:
Договора с фиксированной суммой
Такие договора ещё называются аннуитетными. Например, к таким относится потребительский кредит. Для моделирования EAD аннуитетных договоров могут быть использованы следующие подходы:
- В самом простом случае оценка будущего EAD будет равна значению кредитного обязательства по договору на момент наблюдения.

Такой подход не требует вычислений и является оценкой в первом приближении.
- Второй подход — консервативная оценка EAD: предположим, что заемщик начинает входить в дефолт прямо сейчас, то есть не вносит ни копейки платежей по кредиту, начиная с текущего момента. Тогда к моменту дефолта из штрафов и пени сформируется дополнительный долг, который тоже будет включен в сумму EAD:

где:
— сумма долга на текущую дату,
— сумма накопившихся штрафов и пени, неуплаченных к моменту дефолта,
— прогнозный EAD.
- Менее консервативные методы предполагают, что сумма EAD’а будет представлять собой некую сумму средств, которая лежит в интервале между нулем и консервативным значением, определяемую множителем текущей балансовой позиции. Этот подход будет рассмотрен подробно далее в статье.
Договора с нефиксированной суммой
С нефиксированной суммой, т.н. «револьверные», или «лимитные»: договора, имеющие балансовую и внебалансовую чаcть долга. Внебалансовая часть долга — денежные средства, которые есть возможность использовать, но не использованы на дату наблюдения. Примерами могут быть кредитная карта с лимитом или кредитная линия.
Сумма EAD для такого типа договоров может рассчитываться следующими способами:
- Консервативный подход состоит в том, чтобы считать EAD равным лимиту:

- Другой подход состоит в том, чтобы моделировать некоторый показатель, который будет отражать степень использования внебалансовой части кредита до того, как заемщик окажется в дефолте. Этот подход также будет рассмотрен подробно далее в статье.
Моделирование EAD
Схематично план моделирования EAD изображен на диаграмме:

Формирование витрины для моделирования
Здесь, как и в статьях ранее, мы рассматриваем витрину для моделирования (ABT) как результат объединения трех сущностей: сегмент (id, временная метка, атрибуты сегмента), целевое событие и поведенческие атрибуты.
Начнем с целевого события. Обратим внимание на два его параметра — горизонт и алгоритм сбора. Не стоит забывать, что поскольку событие инициировано фактом дефолта, то все остальные аспекты дефолта (дата начала, дата окончания, тип события) также имеют значение при описании EAD.
Определение горизонта наблюдения

Величина EAD, а также момент дефолта, станут известны только в момент дефолта (сюрприз-сюрприз). Моделировать же его необходимо, выбрав заранее, на каком временнОм интервале планируется прогнозировать дефолт и, соответственно, EAD. Такой интервал называется горизонтом наблюдения. Возможны несколько подходов для учета событий дефолта.
Три наиболее распространенных подхода: метод фиксированного горизонта, когортный и смешанный метод [2].
а) Фиксированный горизонт. Наблюдения формируются таким образом, чтобы от даты наблюдения до даты дефолта временной интервал был фиксированным. При этом длину интервала рекомендуется выбирать таким образом, чтобы она была такой же, как у горизонта наблюдения модели PD для текущего портфеля (например, 12 месяцев).

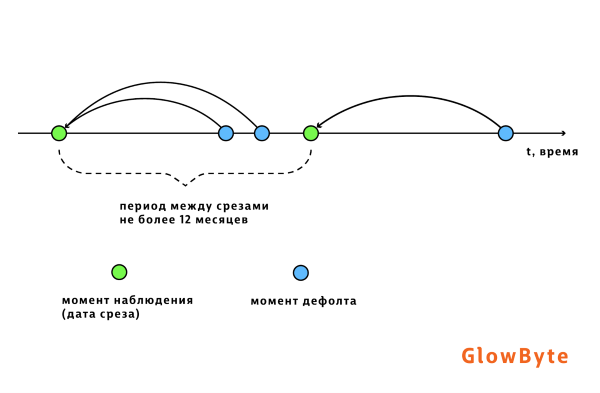

| |
Положительные стороны |
Недостатки |
| Фиксированный интервал |
Простой и понятный горизонт. Легко интерпретируемый результат модели. Однородность выборки. |
Не учитываются события дефолта, наступившие быстрее, чем за 12 месяцев. |
| Когорты |
Учитываются все события дефолта. Учитываются события дефолта, отстоящие на разные временные интервалы от даты наблюдения. |
Необходимо тщательно выбирать длину когорты во избежание смещенности оценки. |
| Смешанный метод |
Учитывается большое количество наблюдений. |
Необходимо проводить дополнительный анализ автокорреляции факторов. |
Формирование сегмента
После того, как определена длина горизонта, необходимо определиться с тем, какие наблюдения попадают в выборку для моделирования.
Обычно подразумевается, что выборкой для моделирования является совокупность договоров, которые в текущий момент не в дефолте, но на горизонте наблюдения в дефолте окажутся.
Имеет место также такой вариант формирования выборки, при котором в момент дефолта одного из договоров, все остальные активные договора заемщика также признаются дефолтными. Этот подход называется дефолтом в результате «инфицирования» и зачастую используется для изменения уровня дефолта.
Определение целевой переменной

Стоит отметить, что в кредитном портфеле встречается большой разброс по балансам: от очень маленьких (на грани материальности) до очень больших значений. Из-за этого прогнозирование непосредственно абсолютного значения баланса может привести к существенной величине ошибки. Чтобы этого избежать, для моделирования используют целевые переменные, которые отражают относительную разницу между актуальным балансом и балансом на дату дефолта (EAD), либо — относительную же разницу между значением лимита и EAD.
В следующем разделе рассмотрим некоторые из них.
Коэффициент кредитной конверсии
Коэффициент кредитной конверсии - credit conversion factor, CCF — та часть доступного лимита, которая будет использована до наступления дефолта [3].

где:
и — это, соответственно, лимит по кредитному договору и баланс на момент наблюдения, — сумма основного и просроченного кредитного долга на момент дефолта.
Поскольку у аннуитетных договоров нет внебалансовой части (то есть, всегда равен нулю), этот подход может применяться только для лимитных договоров.
Выборка для применения представляет собой открытые и недефолтные договора на дату, и рассчитанные для каждого из наблюдений атрибуты, вошедшие в финальную модель. На основании атрибутов рассчитывается CCF для наблюдения. На основании CCF, баланса и лимита рассчитывается прогнозный EAD по следующей формуле:

В этой формуле и — прогнозные значение EAD и CCF соответственно.
Коэффициент использования лимита
Такое целевое событие может быть применено к продуктам с изменяемыми лимитами, что в случае расчета CCF может приводить к отрицательным значениям [4].

Также, как и предыдущий, этот подход может быть применен только для лимитных договоров.
Множитель текущей балансовой позиции
По некоторым револьверным кредитам превышение лимита наступает до момента дефолта. В таком случае подход, основанный на CCF, не имеет смысла ввиду значения больше 100%. Решением подобной проблемы может стать рассмотрение в качестве целевой переменной множителя текущей балансовой позиции.

Прогнозное значение EAD будет иметь следующий вид:

Поскольку в этом подходе расчет EAD опирается только на значение баланса, он может быть использован в том числе для моделирования сегмента аннуитетных договоров.
Использование двух целевых переменных (двухкомпонентная модель)
Общая формула этого подхода выглядит следующим образом:

где:
— баланс на дату наблюдения,
— множитель текущей балансовой позиции,
— коэффициент кредитной конверсии,
— кредитный лимит по договору на дату наблюдения.
Подход можно использовать как для лимитных, так и для аннуитетных договоров:
- для аннуитетов:

где k — это целевая переменная, для которой собираем витрину.
- для лимитных договоров моделируем две целевые переменные:

Когда в кредитном портфеле содержатся договора обоих типов, использование двухкомпонентной модели выгодно отличается от иных подходов, позволяя настроить функционал для каждого сегмента по отдельности.
Таблица сравнения применимости целевых переменных для некоторых случаев
| Рекомендуется к использованию в случаях |
Возможность применения к аннуитетным договорам |
|
| CCF |
Используется в любой непонятной ситуации; есть упоминания в литературе [3][5] |
Нет |
| UT |
В случаях с продуктами с изменяемыми лимитами, а также такими, для которых часто наблюдаются события дефолтов с небольшими значениями EAD |
Нет |
| k |
Может использоваться для продуктов, по которым превышение лимита происходит раньше дефолта. |
Да |
| CCF, k- двухкомпонентная модель |
Используется для портфелей, в которых существенную часть составляют аннуитеты, а также есть предпосылки считать, что лимитные/аннуитетные договора имеет смысл моделировать по отдельности |
Да |
Дополнение
Для задачи резервирования можно рассматривать другие архитектуры модели EAD. Например, при расчете EAD для всего времени жизни договора. Life-time EAD — компонента в рамках МСФО9, которую иногда декомпозируют на две — вероятность и сумму досрочного погашения (prepayment). Это важно, т.к. позволяет «вовремя» перестать резервировать деньги под быстрозакрывающиеся кредитные обязательства.
В более простом варианте, для смежных задач достаточно использовать модель досрочного погашения, т.е. прогноз срока жизни договора.
В более простом варианте, для смежных задач достаточно использовать модель досрочного погашения, т.е. прогноз срока жизни договора.
Расчет ретроспективных значений целевой переменной для всех наблюдений
После того как выбран горизонт событий и целевая переменная, выполняется расчет ее значения для всех наблюдений сегмента.
Поскольку сегмент представляет собой договора, которые попали в дефолт, то для всех них известен EAD. Используя формулы для расчета выбранной на предыдущем шаге целевой переменной, рассчитывается фактическая целевая переменная для наблюдений.
Для некоторых случаев — таких, как двухкомпонентная модель, очевидным шагом будет рассчитать разные целевые переменные для разных сегментов, и возможно, проводить дальнейшее моделирование по каждому из сегментов в отдельности.
Поведенческие атрибуты
Почти все подготовлено для формирования витрины для моделирования. Осталось добавить поведенческие атрибуты. Среди основных драйверов:
- Утилизация по договору;
- Время жизни договора;
- Количество дней в просрочке;
- DTI — debt-to-income ratio — отношение долга к доходам
- PTI — Payment-to-income ratio — отношение ежемесячных платежей по кредиту к доходам
- Размер компании (для ЮЛ)
Полный список смотрите в предыдущей статье цикла.
Выбор типа модели и бинаризация целевой переменной
Перечисленные целевые переменные являются вещественными числами. Вещественная целевая переменная ограничивает выбор типа модели до подмножества регрессионных.
Другим нюансом является тот факт, что в рассматриваемой задаче форма распределения целевой переменной далека от нормальной. Рассмотрим пример распределения целевой функции CCF [3]:

Распределение CCF часто характеризуется пиками около CCF = 0 и CCF = 1. Такое распределение может привести к неточному прогнозу модели стандартной линейной регрессии. В этом случае можно использовать GLM — обобщенную модель линейной регрессии — с некоторой функцией связи (link function), которая учитывает распределение целевой переменной, отличное от нормального [6]. Тем не менее, это требует дополнительного анализа на предмет функции связи, который необходимо проводить заново для каждого моделируемого портфеля. По этим причинам, иногда целесообразно бинаризовать целевую переменную, и использовать классификационную модель.
Существует несколько способов бинаризовать целевую переменную [7].
Немного про бинаризацию
Для того, чтобы преобразовать вещественную целевую переменную в бинарную, можно выбрать некий порог, выше которого значение равно единице, а ниже - нулю:
 где – выбранное пороговое значение.
где – выбранное пороговое значение.
В этом случае пороговое значение — гиперпараметр модели, и подбирать его следует на выборке для валидации.
Другой подход заключается в том, что каждое наблюдение витрины для моделирования дублируется. Для одного из дублированных наблюдений значение CCF принимается равным 1, а для другого — 0. Дополнительно, каждому из дублированных наблюдений присваиваются веса, которые равны CCF и 1 — CCF соответственно.
Вот для примера таблица, которая получается путем подобного преобразования.

Отсечение по фиксированному пороговому значению
Для того, чтобы преобразовать вещественную целевую переменную в бинарную, можно выбрать некий порог, выше которого значение равно единице, а ниже - нулю:

В этом случае пороговое значение — гиперпараметр модели, и подбирать его следует на выборке для валидации.
Взвешенный метод
Другой подход заключается в том, что каждое наблюдение витрины для моделирования дублируется. Для одного из дублированных наблюдений значение CCF принимается равным 1, а для другого — 0. Дополнительно, каждому из дублированных наблюдений присваиваются веса, которые равны CCF и 1 — CCF соответственно.
Вот для примера таблица, которая получается путем подобного преобразования.
| ID |
Предиктор_1 |
Предиктор_2 |
CCF |
| 1 |
100 |
1 |
0.9 |
| 2 |
150 |
0.5 |
0.6 |
| 3 |
50 |
0.9 |
0.7 |

| ID |
Предиктор_1 |
Предиктор_2 |
Вес |
Таргет |
| 1 |
100 |
1 |
0.9 |
1 |
| 1 |
100 |
1 |
0.1 |
0 |
| 2 |
150 |
0.5 |
0.6 |
1 |
| 2 |
150 |
0.5 |
0.4 |
0 |
| 3 |
50 |
0.9 |
0.7 |
1 |
| 3 |
50 |
0.9 |
0.3 |
0 |
Изначально CCF означал долю неиспользованного на текущий момент лимита, которую заемщик израсходует к моменту выхода в дефолт.
Бинаризованный же CCF может принимать только два значения:

По сути, сформулирована классификационная задача, для решения которой можно использовать любой из подходящих алгоритмов машинного обучения. Впрочем, часто останавливаются на логистической регрессии. В случае бинаризации взвешенным методом — на взвешенной логистической регрессии (weighted logit regression). Выбор именно логистической регрессии обусловлен тем, что она интерпретируема и классически широко используется в моделях кредитного моделирования, в первую очередь, моделях PD.
Прогноз модели — вероятность наступления события CCFbinary = 1 — лежит в интервале от 0 до 1. При применении модели его можно интерпретировать как прогнозную оценку оригинальной, вещественной переменной CCF.
Применяя таким образом модель и зная значения баланса и лимита, рассчитывается прогнозное значение EAD по формуле из раздела о CCF:

Заключение и вывод
EAD — несложная, по сравнению с PD и LGD, компонента для моделирования. Как правило, для быстрого построения качественного baseline можно воспользоваться одной из рассмотренных траекторий. Сборка модульная. Отбор признаков и все оттенки ML для финальной модели могут быть подобраны исходя из предложенного нами ранее pipeline.
- Использование смешанного горизонта;
- Двухкомпонентная модель (CCF и k). Факторы, включенные в модель, выбраны так, чтобы наиболее полно характеризовать заемщика и его платежную дисциплину.
- Для моделирования можно использовать обычную logit-регрессию, предварительно выполнив бинаризацию целевой переменной CCF взвешенным методом.
- Проверка качества модели на out-of-time тестовой выборке.
Итоговый выбор, безусловно, осуществляется после полного погружения в данные и бизнес-процессы, а также требования к процессу применения моделей.
Авторы статьи: Алиса Пугачёва (alisaalisa), Александр Бородин (abv_gbc)
Список использованных терминов и сокращений
- ABT — analytical base table – витрина данных для моделирования [8].
- EL – expected loss – ожидаемые потери по договору.
- PD – probability of default – вероятность дефолта.
- LGD – loss given default – доля EAD, которую клиент не возвращает на горизонте восстановления.
- EAD – exposure at default – кредитные обязательства по договору на момент дефолта. По сути, баланс на дату дефолта, где баланс = Тело долга + Просрочка.
- CCF – credit conversion factor — часть доступных на момент наблюдения средств, которая будет использована клиентом к моменту дефолта.
- Дефолт – это невыполнение обязательств по договору займа. Обычно, дефолтом считается неоплата по договору в течение 90 дней.
- ОД – основной долг.
- ПОД – просроченный основной долг.
- Балансовая часть долга — сумма долга на момент наблюдения. Баланс = ОД + ПОД.
- Внебалансовая часть долга — сумма средств, которые доступны для использования, но пока не использованы. Применимо к лимитным договорам.
- GLM – generalized linear model.
- DS — data science.
- ML – machine learning.
- Out-of-time – способ разделения на обучающую и тестовую выборки. Разделение происходит способ по временной метке наблюдений так, чтобы в трейн-выборке оказались более ранние наблюдения, а в тестовой — более поздние.
Ссылки
- ML и DS оттенки кредитного риск-менеджмента
- ТЕОРЕТИЧЕСКИЕ И ПРАКТИЧЕСКИЕ АСПЕКТЫ ПОСТРОЕНИЯ EAD-МОДЕЛЕЙ
- ПОСТРОЕНИЕ РЕГРЕССИОННЫХ МОДЕЛЕЙ ДЛЯ ОЦЕНКИ ВЕЛИЧИНЫ СРЕДСТВ ПОД РИСКОМ (EAD)
- Predictive Models for Credit Limit Utilization
- Exposure at default models with and without the credit conversion factor
- Practitioner's Guide to Generalized Linear Models
- Bart Baesens «Credit Risk Analysis»
- https://en.wikipedia.org/wiki/Analytical_base_table


vakhramov
Изза подобных упрощений банки сами же и страдают :) При текущих компетенциях банковского менеджмента и политике ЦБ ожидаемые потери будут стремиться не к нулю для банка относительно всех граждан РФ, ввязавшихся в полукомпетентную сделку с банками (особенно ВТБ24).
alisaalisa Автор
Из-за подобных комментариев вся предметная дискуссия сводится к холивару :)
vakhramov
С чего-то надо начинать :) Меня-то этот вопрос уже 4 год тревожит изза плохого документооборота приставов с налоговой и судами, помноженное на операционно-технические глупости менеджмента ВТБ24 (ныне ВТБ, как я понял). Я как мог консультировал их при каждом звонке по 50 рублей в минуту (в кредит), и очень сильно не согласен с тем, кто кому должен))
И ведь я далеко не один такой, пострадавший от бездействия банка