Есть целая куча популярных задач для собеседований, которые можно решить одним из двух способов: или логичным применением стандартных структур данных и алгоритмов, или использованием некоторых свойств XOR сложным для понимания способом.
Хоть и непривычно ожидать решения с XOR на собеседованиях, довольно забавно разбираться, как они работают. Оказывается, все они основаны на одном фундаментальном трюке, который я постепенно раскрою в этом посте. Далее мы рассмотрим множество способов применения этого трюка с XOR, например, при решении популярной задачи с собеседований:
Дан массив из n — 1 целых чисел, находящихся в интервале от 1 до n. Все числа встречаются только один раз, за исключением одного числа, которого нет. Найдите отсутствующее число.
Разумеется, существует множество прямолинейных способов решения этой задачи, однако есть и довольно неожиданный, в котором применяется XOR.
XOR
XOR — это логический оператор, работающий с битами. Давайте обозначим его
^. Если два получаемых им на входе бита одинаковы, то результат будет равен 0, в противном случае 1.При этом применяется операция исключающего ИЛИ — чтобы результат был равен
1, только один аргумент должен быть равен 1. Можно показать это с помощью таблицы истинности:x |
y |
x ^ y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
В большинстве языков программирования
^ реализован как побитовый оператор, то есть XOR по отдельности применяется к каждому биту в строке битов (например, в байте).Пример:
0011 ^ 0101 = 0110так как
0 ^ 0 = 0
0 ^ 1 = 1
1 ^ 0 = 1
1 ^ 1 = 0Благодаря этому мы можем применять XOR к чему угодно, а не только к булевым значениям.
Выявляем полезные свойства
Из представленного выше определения можно вывести несколько свойств. Давайте разберём их по порядку, а затем скомбинируем их для решения задач с собеседований.
XOR и 0: x ^ 0 = x
Если одним из аргументов XOR является
0, то второй аргумент является результатом. Это непосредственно следует из таблицы истинности, достаточно посмотреть на строки, где y = 0 (первая и третья строка).x |
y |
x ^ y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
XOR с одинаковыми аргументами: x ^ x = 0
Если два аргумента одинаковы, то результат всегда равен
0. Мы можем убедиться в этом, снова взглянув на таблицу истинности. На этот раз нужно посмотреть на строки, где x = y (первая и последняя).x |
y |
x ^ y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Это означает, что применив XOR к одинаковым аргументам, мы их взаимно уничтожим.
Коммутативность: x ^ y = y ^ x
Операция XOR коммутативна, то есть мы можем менять порядок применения XOR. Чтобы доказать это, можно взглянуть на таблицу истинности
x ^ y и y ^ x:x |
y |
x ^ y |
y ^ x |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
Как мы видим,
x ^ y и y ^ x всегда дают одинаковые значения.Последовательности операций XOR
Скомбинировав всё это, мы можем вывести главную мысль, стоящую в основе всего дальнейшего:
Трюк с XOR: если у нас есть последовательность операций XOR a ^ b ^ c ^ ..., то из неё можно убрать все пары повторяющихся значений, и это не повлияет на результат.Коммутативность позволяет нам изменить порядок применения XOR, чтобы повторяющиеся элементы находились рядом друг с другом. Так как
x ^ x = 0 и a ^ 0 = a, каждая пара повторяющихся значений не будет влиять на результат.Давайте разберём пример:
a ^ b ^ c ^ a ^ b # Commutativity
= a ^ a ^ b ^ b ^ c # Using x ^ x = 0
= 0 ^ 0 ^ c # Using x ^ 0 = x (and commutativity)
= cТак как
^ — побитовый оператор, это будет работать вне зависимости от типа значений a, b и c. Эта идея лежит в основе многих применений XOR, которые могут показаться магическими.Способ применения 1: перемена значений местами
Прежде чем приступать к задаче поиска отсутствующего числа, давайте начнём с более простой задачи:
Поменяйте местами два значения x и y без использования вспомогательных переменных.
Оказывается, эту задачу можно легко решить при помощи трёх команд XOR:
x ^= y
y ^= x
x ^= yЭто кажется довольно загадочным. Почему при этом
x и y поменяются местами?Чтобы понять, как это происходит, давайте разберёмся пошагово. В комментарии после каждой команды указаны текущие значения
(x, y):x ^= y # => (x ^ y, y)
y ^= x # => (x ^ y, y ^ x ^ y) = (x ^ y, x)
x ^= y # => (x ^ y ^ x, x) = (y, x)Воспользовавшись выведенными ранее свойствами, мы видим, что это на самом деле так.
Фундаментальным открытием здесь является то, что при наличии
x ^ y в одном регистре и x в другом мы можем совершенно точно воссоздать y. После сохранения x ^ y (команда 1) мы можем просто поместить x в другой регистр (команда 2), а затем использовать его для замены x ^ y на y (команда 3).Способ применения 2: поиск отсутствующего числа
Давайте наконец решим задачу, представленную в начале поста:
Дан массив A из n — 1 целых чисел, находящихся в интервале от 1 до n. Все числа встречаются в нём ровно один раз, за исключением одного отсутствующего числа. Найти это отсутствующее число.Разумеется, есть множество прямолинейных решений этой задачи, но мы решили использовать XOR.
Из трюка с XOR мы знаем, что имея последовательность операторов XOR, можно убрать из неё все повторяющиеся аргументы. Однако если мы просто применим XOR ко всем значениям массива, то не сможем воспользоваться этим трюком, потому что в нём нет одинаковых значений:
A[0] ^ A[1] ^ ... ^ A[n - 2]Обратите внимание, что
A[n - 2] — последний индекс списка из n - 1 элементов.Дополнительно мы можем выполнить XOR для всех значений от 1 до n:
1 ^ 2 ^ ... ^ n ^ A[0] ^ A[1] ^ ... ^ A[n - 2]Так мы получим последовательность операторов XOR, в которой элементы встречаются следующим образом:
- Все значения из исходного массива теперь встречаются дважды:
- один раз из-за взятия всех значений от 1 до n
- один раз, потому что они были в исходном массиве
- Отсутствующее значение встречается только один раз:
- из-за взятия всех значений от 1 до n
Применив ко всему этому XOR, мы, по сути, уберём все встречающиеся дважды значения благодаря трюку с XOR. Это значит, что останется только отсутствующее значение, то есть именно то, которое мы и искали.
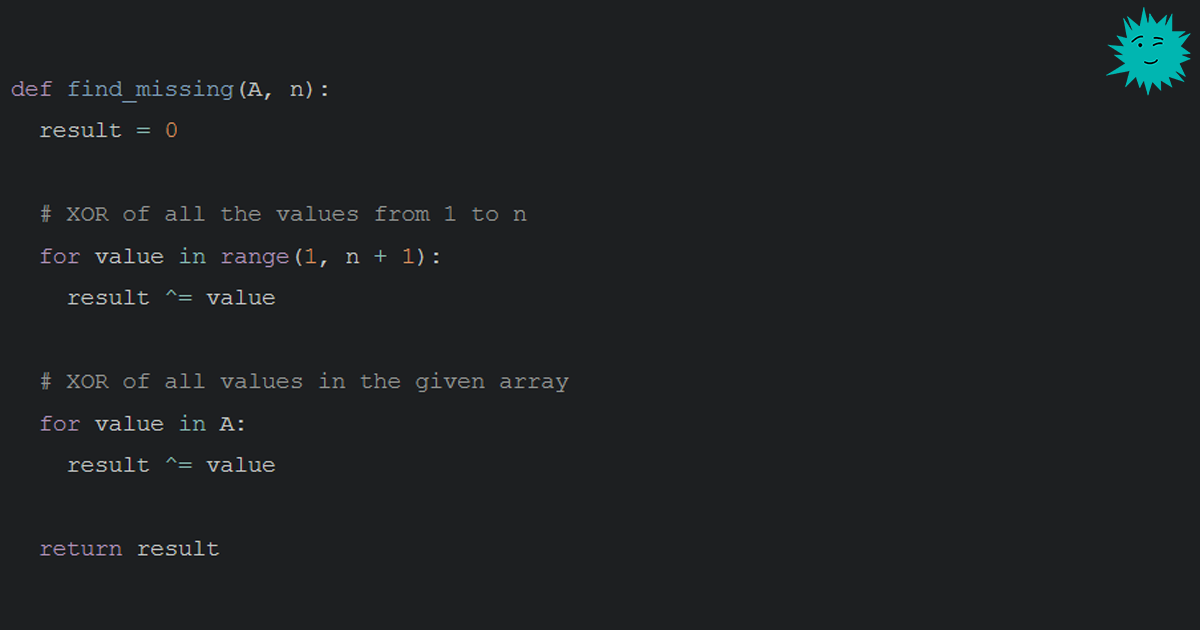
В коде это будет выглядеть примерно так:
def find_missing(A, n):
result = 0
# XOR of all the values from 1 to n
for value in range(1, n + 1):
result ^= value
# XOR of all values in the given array
for value in A:
result ^= value
return resultС первого взгляда на код алгоритм понять сложно. Однако если знать, как работает трюк с XOR, то он становится довольно тривиальным. По-моему, именно поэтому не стоит ждать такого решения на собеседованиях: оно требует знания очень специфичного трюка, но почти никакого алгоритмического мышления.
Прежде чем мы перейдём к следующему способу применения, я сделаю пару замечаний.
Использование этого трюка не только для целых чисел
Хоть мы пока работали только с целыми числами от 1 до n, это необязательно. На самом деле, предыдущий алгоритм работает в любой ситуации, где есть (1) некоторое множество потенциальных элементов и (2) множество действительно встречающихся элементов. Эти множества могут отличаться только одним отсутствующим элементом. Это замечательно сработало для целых чисел, потому что множество потенциальных элементов соответствует элементам от 1 до n.
Можно придумать способы применения, где элементы не являются целыми числами от 1 до n:
- Множество потенциальных элементов — это объекты
Personи нам нужно найтиPerson, отсутствующего в списке значений - Множество потенциальных элементов — все узлы графа, и мы ищем отсутствующий узел
- Множество потенциальных элементов — просто целые числа (необязательно с 1 до n) и нам нужно найти отсутствующее целое число
Арифметические операции вместо XOR
Если алгоритм по-прежнему кажется вам непостижимым и магическим (надеюсь, это не так), то может быть полезным подумать, как достичь того же результата при помощи арифметических операторов. На самом деле всё довольно просто:
def find_missing(A, n):
result = 0
# Add all the values from 1 to n
for value in range(1, n + 1):
result += value
# Subtract all values in the given array
for value in A:
result -= value
return resultМы складываем все потенциальные целые числа, а затем вычитаем те, которые встречаются на самом деле. Это решение не такое красивое, потому что придётся обрабатывать переполнения, а также потому что тип элементов должен поддерживать
+, - с определёнными свойствами. Однако здесь используется та же логика взаимного уничтожения элементов, потому что они встречаются определённое количество раз (один раз как положительное, другой — как отрицательное).Способ применения 3: поиск повторяющегося числа
И вот здесь всё становится интереснее: мы можем применить точно такое же решение к похожей задаче с собеседования:
Дан массив A из n + 1 целых чисел, находящихся в интервале от 1 до n. Все числа встречаются ровно один раз, за исключением одного числа, которое повторяется. Найти это повторяющееся число.Давайте подумаем, что произойдёт, если мы просто применим алгоритм из предыдущего решения. Мы получим последовательность операторов XOR, в которой элементы встречаются следующим образом:
- Повторяющееся значение встречается три раза:
- один раз из-за взятия всех значений от 1 до n
- дважды, потому что оно повторяется в исходном массиве
- Все остальные значения встречаются дважды:
- один раз из-за взятия всех значений от 1 до n
- один раз, потому что они были уникальными в исходном массиве
Как и ранее, все повторяющиеся элементы взаимно уничтожаются. Это означает, что у нас осталось именно то, что мы ищем: элемент, повторяющийся в исходном массиве. Встречающийся три раза элемент в сочетании с XOR сводится к этому самому элементу:
x ^ x ^ x
= x ^ 0
= xВсе остальные элементы взаимно уничтожаются, потому что встречаются ровно два раза.
Способ применения 4: поиск двух отсутствующих/повторяющихся чисел
Оказывается, мы можем расширить возможности алгоритма. Рассмотрим чуть более сложную задачу:
Дан массив A из n — 2 целых чисел, находящихся в интервале от 1 до n. Все числа встречаются ровно один раз, за исключением двух отсутствующих чисел. Найти эти два отсутствующих числа.Как и ранее, задача полностью эквивалентна поиску двух повторяющихся чисел.
Как вы наверно догадались, мы будем придерживаться того, что сработало раньше, и начнём точно так же: рассмотрим, что произойдёт, если использовать предыдущий алгоритм с XOR. Если мы его применим, то получим последовательность операторов XOR, в которой все элементы взаимно уничтожают друг друга, за исключением тех, которые мы ищем.
Обозначим эти элементы как
u и v, просто потому, что раньше эти буквы не использовали. После применения предыдущего алгоритма у нас останется u ^ v. Что можно сделать с этим значением? Нам каким-то образом нужно извлечь из него значения u и v, но не совсем понятно, как это сделать.Разделение при помощи изучения u ^ v
К счастью, мы можем понять, что делать, воспользовавшись изложенным выше. Давайте подумаем:
Если два входных бита XOR одинаковы, то результат равен0, в противном случае1.
Если проанализировать отдельные биты в
u ^ v, то каждый 0 будет означать, что бит имеет одинаковое значение в u и v. Каждая 1 означает, что биты различаются.Благодаря этому мы найдём первую
1 в u ^ v, т.е. первую позицию i, в которой u и v должны различаться. Затем мы разделим A, а также числа от 1 до n в соответствии с этим битом. В результате мы получим два сегмента, каждый из которых содержит два множества:- Сегмент
0
- Множество всех значений от 1 до n, в которых
i-тый бит равен0 - Множество всех значений из A, в которых
i-тый бит равен0
- Множество всех значений от 1 до n, в которых
- Сегмент
1
- Множество всех значений от 1 до n, в которых
i-тый бит равен1 - Множество всех значений из A, в которых
i-тый бит равен1
- Множество всех значений от 1 до n, в которых
Так как
u и v различаются в позиции i, то мы знаем, что они должны быть в разных сегментах.Упрощаем задачу
Далее мы можем использовать ещё одно сделанное ранее открытие:
Хоть пока мы работали только с целыми числами от 1 до n, это необязательно. На самом деле, предыдущий алгоритм работает в любой ситуации, где есть (1) некоторое множество потенциальных элементов и (2) множество действительно встречающихся элементов. Эти множества могут отличаться только одним отсутствующим (или повторяющимся) элементом.
Эти два множества точно соответствуют множествам, находящимся в каждом из сегментов. Следовательно, мы можем выполнить поиск
u, применив этот принцип к одному из сегментов и найдя отсутствующий элемент, а затем найти v, применив его к другому сегменту.На самом деле это очень удобный способ решения задачи: по сути, мы сводим данную новую задачу к более общей версии решённой ранее задачи.
Достигнуть предела
Можно попробовать пойти ещё дальше и попытаться решить задачу с тремя и более отсутствующими значениями. Я не особо это обдумывал, но считаю, что на этом наши успехи с XOR закончатся. Если отсутствует (или повторяется) больше двух элементов, то анализ отдельных битов выполнить не удастся, поскольку существует множество сочетаний для результатов в виде
0 и 1.Следовательно, задача требует более сложных решений, больше не использующих XOR.
Заключительные мысли
Как говорилось выше, наверно, не стоит давать такие задачи на собеседованиях. Для их решения нужно знать не сразу понятный трюк, но если он известен, то решать больше практически нечего (возможно, за исключением способа применения 4). Едва ли таким образом кандидат продемонстрирует алгоритмическое мышление (кроме навыков упрощения) и здесь не особо получится использовать структуры данных.
Однако здорово было выяснить, как этот трюк работает. Похоже, XOR обладает идеально подходящими для этой задачи свойствами. Кроме того, есть некая красота в том, что нечто столь фундаментальное, как XOR, можно использовать для создания описанных в статье алгоритмов.
На правах рекламы
VDSina предлагает виртуальные серверы на Linux и Windows — выбирайте одну из предустановленных ОС, либо устанавливайте из своего образа.



kovserg
У xor-а есть куда более практичное применение — коды Грея

Kohelet
И код Хэмминга. Хотя в википедии в алгоритмах кодирования/декодирования что-то с матрицами наворочено, на самом деле идея простая — xor номеров единичных битов.
kovserg
Да это проще Рида-Соломона, но более расточительно. Вот пример кодирования 8бит в 12бит способное восстановить один ошибочный бит.