Про trie на хабре уже писали.
Структура array mapped trie
В trie достаточно часто хранят строки, поэтому есть понятие алфавита, из которого могут состоять элементы. Для оптимизации под x32 ограничивают размер алфавита до 32 ( 0 — 31 ).
Давайте посмотрим, как выглядит array mapped trie, оно же AMT ( взято из [1] ):

AMT состоит из узла и нескольких отрезков, соединяющих наш узел и другие узлы. Каждый отрезок представляет собой один из возможных символов алфавита.
В узле хранится 32-битная структура ( bitmap ), каждый бит структуры отражает состояние одного из 32 отрезков ( 0 — нет, 1 — есть ). Также в узле находится таблица, в которой хранятся указатели на поддеревья или последние символы в данной подстроке ( листья ). Указатели в таблице хранятся упорядоченно, и каждому из указателей соответствует бит = 1 в битовой структуре.
Пример: чтобы найти символ 's', надо идти по битовой структуре до соответствующего бита. Пока идем по структуре — считаем биты = 1 ( взведенные биты ). Допустим, мы насчитали 5 взведенных битов, а бит, соответствующий 's', оказался 6-ым взведенным битом. Соответственно, нам нужен 6-ой указатель в таблице данного узла. Если бит оказался невзведенным ( = 0 ), то данного символа нет.
Структура hash array mapped trie
Теперь перейдем к HAMT. Вместо алфавита используются старшие биты хэша. Вот как выглядит HAMT ( взято из [1] ):
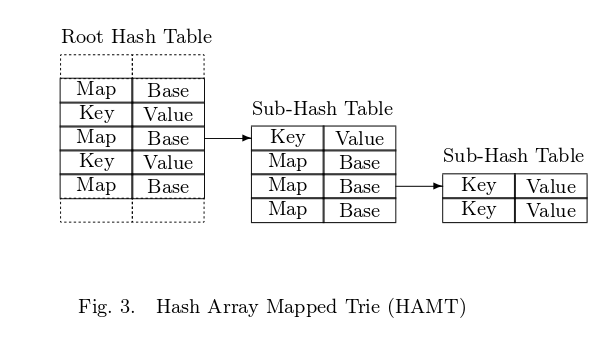
HAMT состоит из главной хэш таблицы размером 2 ^ t, где обычно t >= 5. Каждый элемент главной таблицы:
1. либо корневой узел дерева подтаблиц с размером 32
Index Node:
int bitmap (32 bits)
Node*[] table (max length of 32)
2. либо просто пара ключ — значение
Key Value Node:
K key
V value
Выбор хэш-функции зависит от вашего набора данных. Желательно выбрать хэш-функцию, дающую минимальное количество коллизий ( подробнее про коллизии в [2] ).
Поиск элемента
1. Генерируем 32-битный хэш для ключа.
2. Из получившегося хэша берем t старших бит ( примечание: t старших бит берем только в первый раз, в остальные — по 5 бит ) и используем их как индекс в таблице. Тут возможно 3 варианта:
a) в ячейке с таким индексом ничего нет — такого ключа нет в таблице;
b) в ячейке есть одна пара ключ / значение. Если ключ совпал — нашли элемент, не совпал — не нашли;
c) в ячейке хранится 32-битный bitmap и таблица с указателями. В этом случае берем следующие 5 бит хэша и снова используем их как индекс в bitmap. Если бит не взведен, то такого ключа нет, если взведен — то считаем все взведенные биты с начала по текущий ( как и в AMT ). Таким образом мы получили номер необходимого указателя в таблице. Идем по указателю и повторяем алгоритм.
Часто необходимо всего несколько итераций этого алгоритма ( хотя это зависит от заполненности дерева ). Ключ сравнивается всего один раз — когда мы попали в ситуацию b. Отсутствие ключа детектируется тоже достаточно рано.
Вставка элемента
Повторяем шаги из алгоритам вставки, пока не произойдет одна из 3 ситуаций:
a) в ячейке с таким индексом ничего нет;
b) в ячейке хранится 32-битный bitmap и таблица с указателями;
В обоих случаях алгоритам простой: если вставка происходит в главную таблицу — то просто вставляем пару ключ / значение. Если же вставка происходит в подтаблицу, то взводим соответствующий бит, аллоцируем новую таблицу указателей, копируем в неё указатели из старой таблицы и новый указатель на нашу пару, а старую таблицу удаляем.
В итоге у нас взведен бит соответствующей ячейки, в таблице указателей все старые указатели, а также в соответствующей ячейке новый указатель.
c) произошла коллизия — т. е. у нас совпала какая-то часть двух хэшей. Решение простое — создаем новую подтаблицу, от уже существующего ключа вычисляем хэш и используем очередные 5 бит для нахождения нужной ячейки. Взводим бит в данной ячейке, вставляем в таблицу указателей указатель на существующую пару ключ / значение, возвращаемся к вставляемой паре, берем тоже очередные 5 бит и ищем нужную ячейку. Этот шаг с созданием новой подтаблицы повторяем до тех пор, пока коллизия не исчезнет.
С каждым таким шагом вероятность коллизии уменьшается в 32 раза ( размер таблицы указателей и bitmap ).
Иногда мы получаем полную коллизию — все 32 бита хэшей двух разных ключей совпадают. Тогда берем следующую хэш-функцию и хэшируем ей два конфликтующих ключа. В итоге когда будем искать по ключу элемент — мы пройдем по всем битам первичного хэша, увидим, что пришли не в лист, а в подтаблицу, и вычислим новый хэш ключа с помощью второй функции.
Вообще, это не единственный способ решения коллизий, в разных реализациях есть другие. Автор в своей работе предлагает использовать ту же хэш-функцию, просто после коллизии подавать ей на вход ключ и уровень дерева, в котором мы находимся в данный шаг алгоритма ( 0 — корневая таблица и т. д. ). Если же приложению критически важно, чтобы время операции вставки было ограничено сверху ( чисто теоретически мы можем взять два таких ключа, что их хэши будут совпадать после нескольких вызовов функции рехэширования, а значит, операция вставки будет длиться очень долго ), то вместо рехэширования совпадающих ключей можно использовать сами ключи.
Распределение памяти
Нам понадобяться пулы от 1 до 32 элементов ( для таблиц различного размера ). Выделяем блоки памяти и разбиваем на соответствующие таблицы. В процессе работы постепенно будет увеличиваться фрагментация. Для того, чтобы вернуть память, необходимо проводить дефрагментацию. Можно установить лимит на объем фрагментированной памяти в процентах, проверять его при вставке элемента и при превышении лимита — проводить дефрагментацию. Операцию дефрагментации можно реализовать как О(1) операцию.
Изменение размера корневой таблицы
В какой-то момент времени дерево вырастет настолько, что увеличение размера корневой таблицы даст ощутимый прирост в скорости. Каждая подтаблица имеет 32 элемента, поэтому наиболее логичным будет изменение с 2 ^ t до 2 ^ ( t + 5 ). При увеличении размера все подтаблицы первого уровня попадают в корневую таблицу. Причем рехэширование нужно только в случае, когда у нас в корневую таблицу попадают листы дерева ( нужно заново вычислять хэш чтобы определить новое положение элемента ). В остальных случаях просто копируем элементы из подтаблицы в корневую таблицу.
Возможно не сразу копировать все подтаблицы в корневую таблицу, а постепенно. При этом запоминается индекс переноса. Все элементы ниже индекса копируются в новую таблицу, а индекс постепенно продвигается по старой таблице. Во время поиска происходит сравнение первых t бит хэша с индексом переноса — если хэш больше, то поиск направляется в старую таблицу, иначе — в новую. Алгоритм вставки тоже должен учитывать индекс переноса.
Когда стоит проводить увеличение корневой таблицы? Когда размер новой таблицы будет занимать 1 / f от всего дерева. Параметр f надо подбирать исходя из конкретной ситуации.
Объем необходимой памяти
Объем памяти зависит от индекса переноса. Автор в своей работе привел таблицу, показывающую эту зависимость ( взято из [1] )
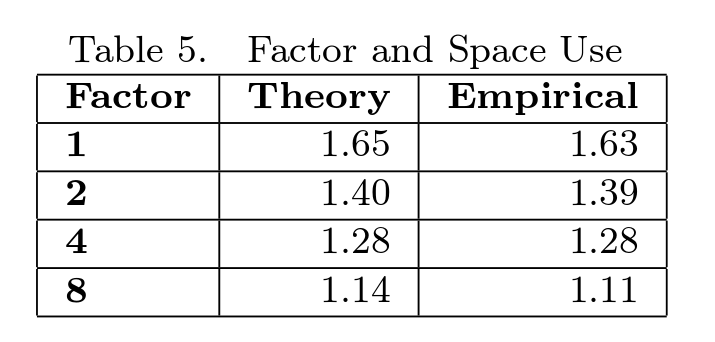
Т. е. если индекс переноса = N / 4, где N — количество вставленных в дерево пар ключ-значение, то занимаемая память пропорциональна 1.28 * N.
Удаление элемента
Во время удаления могут возникнуть две ситуации:
a) удаляем элемент в подтаблице с количеством элементов больше 2. Тогда надо перенести все остальные элементы в меньшую по размеру подтаблицу, а текущую пометить пустой.
b) удаляем элемент в подтаблице с количеством элементов равным 2. В этой ситуации оставшийся элемент просто переносим в подтаблицу уровнем выше, а текущую помечаем пустой.
Исходный код
Я потерял ссылку на реализацию от автора на С(( Кто найдет — напишите в комментарии.
github.com/yasm/yasm/blob/master/libyasm/hamt.c — пример реализации на С. Ссылки на примеры реализации на других языках можно найти в [3].
Ссылки
[1] статья от автора алгоритма
[2] статья про коллизии хэшей на Википедии
[3] статья про HAMT на Википедии
[4] хороший вопрос на SO
[5] краткий вводный курс в HAMT
Замечания и неточности пишите в комментариях, орфографические ошибки и потерявшиеся знаки препинания присылайте в личку.
Комментарии (6)

schroeder
15.09.2015 10:19+3не подскажите, чем лучше эта структура обычной явовской HashMap?

Ramires
15.09.2015 11:05+21. HashMap не потоко-безопасна. HAMT можно реализовать потоко-безопасным ( это не так уж сложно ). Конечно, есть ConcurrentHashMap. Я не пишу на Java, так что ничего не могу сказать про быстродействие.
2. К HAMT можно написать итераторы и обходить как простое дерево, HashMap обходить в определенном порядке, кажется, нельзя.
Еще хороший пример использования HAMT при передаче файлов.
Вообще, всё что я написал выше, применимо ко всем hash trees.
Можно поискать статьи типа «Hash map vs hash tree» для изучения.
Насчет производительности нашел такой набор слайдов. Тут, правда, Haskell, но можно взглянуть на приведенные на последнем слайде цифры.

cs0ip
19.09.2015 22:55+1Ещё одно важное отличие — поддержка персистентности. Т.е. если мы используем данную структуру для реализации иммутабельной структуры данных, то при необходимости создать копию с одним измененным элементом, мы можем не копировать всю структуру, а скопировать только один листовой узел с 32 элементами, что значительно экономит память в функциональных языках.


MuLLtiQ
Насколько я знаю, эта структура данных используется в функциональных языках для реализации «иммутабельных» структур данных — вектора, словаря, множества.
cs0ip
По крайней мере в scala для вектора используется AMT, а не HAMT. А вообще несколько не хватает примеров использования подобных структур. Как удачных, так и неудачных (что не менее важно). Потому что, если смотреть формально на тот же вектор, то, допустим время модификации элемента O(1) (ну т.е. создание нового вектора на основе старого), но на практике ~32 раза медленнее чем в обычном массиве. И хотя иммутабельность хорошо, но при частых модификациях врядли удасться себе такое позволить.