Привет, хабр!
Как и обещал, продолжаю публикацию разборов задач, которые я прорешал за время работы с ребятами из MLClass.ru. В этот раз мы разберем метод главных компонент на примере известной задачи распознавания цифр Digit Recognizer с платформы Kaggle. Статья будет полезна новичкам, которые еще только начинают изучать анализ данных. Кстати, еще не поздно записаться на курс Прикладной анализ данных, получив возможность максимально быстро прокачаться в данной области.
Данная работа является естественным продолжением исследования, изучающего зависимость качества модели от размера выборки. В ней для была показана возможность уменьшения количества используемых объектов в обучающей выборке с целью получения приемлемых результатов в условиях ограниченных вычислительных ресурсов. Но, кроме количества объектов, на размер данных влияет и количество используемых признаков. Рассмотрим эту возможность на тех же данных. Используемые данные были подробно изучены в предыдущей работе, поэтому просто загрузим тренировочную выборку в R.
Как мы уже знаем данные имеют 42000 объектов и 784 признака, представляющие собой значение яркости каждого из пикселей составляющего изображение цифры. Разобъём выборку на тренировочную и тестовую в соотношении 60/40.
Теперь удалим признаки, имеющие константное значение.
В итоге осталось 253 признака.
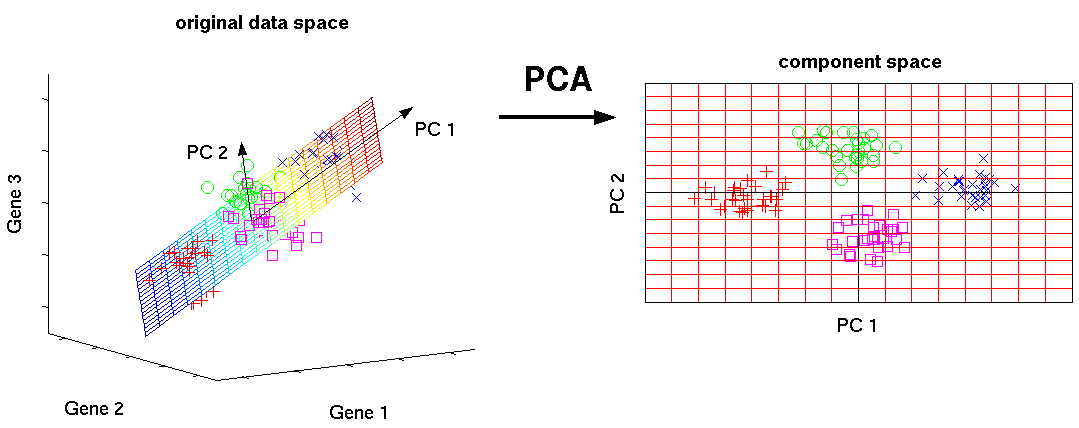
Метод главных компонент (PCA) преобразует базовые признаки в новые, каждый из которых является линейной комбинацией изначальных таким образом, что разброс данных (то есть среднеквадратичное отклонение от среднего значения) вдоль них максимален. Метод применяется для визуализации данных и для уменьшения размерности данных (сжатия).
Для большей наглядности случайным образом отберём из тренировочной выборки 1000 объектов и изобразим их в пространстве первых двух признаков.
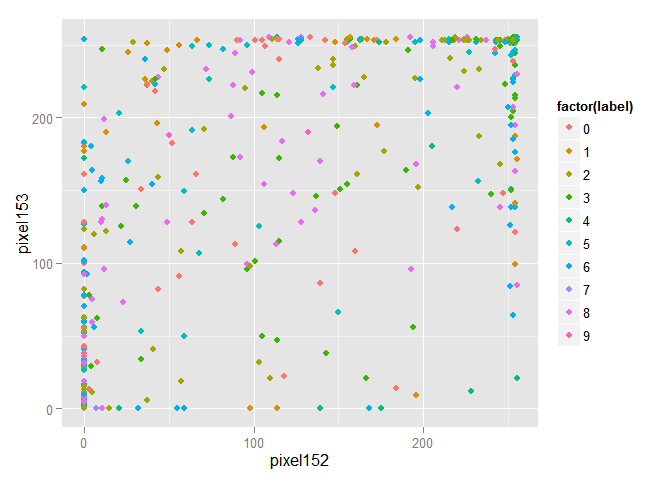
Очевидно, что объекты перемешаны и выделить среди них группы объектов принадлежащих одному классу проблематично. Проведём преобразование данных по методу главных компонент и изобразим в пространстве первых двух компонент. Замечу, что компоненты расположены в убывающем порядке в зависимости от разброса данных, который приходится вдоль них.
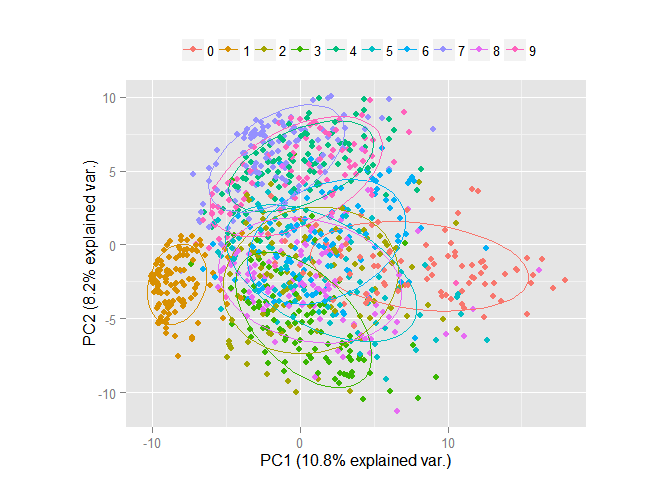
Очевидно, что даже в пространстве всего лишь двух признаков уже можно выделить явные группы объектов. Теперь рассмотрим те же данные, но уже в пространстве первых трёх компонент.
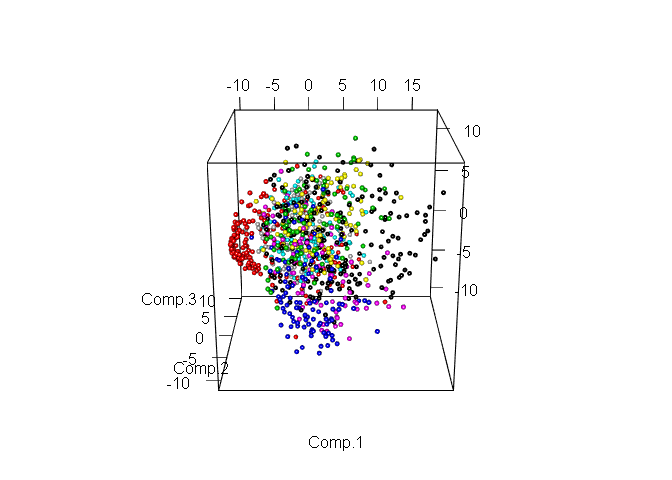
Выделение различных классов ещё больше упростилось. Теперь выберем количество компонент, которое будем использовать для дальнейшей работы. Для этого посмотрим на соотношение дисперсии и количество компонент объясняющие её, но уже используя всю тренировочную выборку.
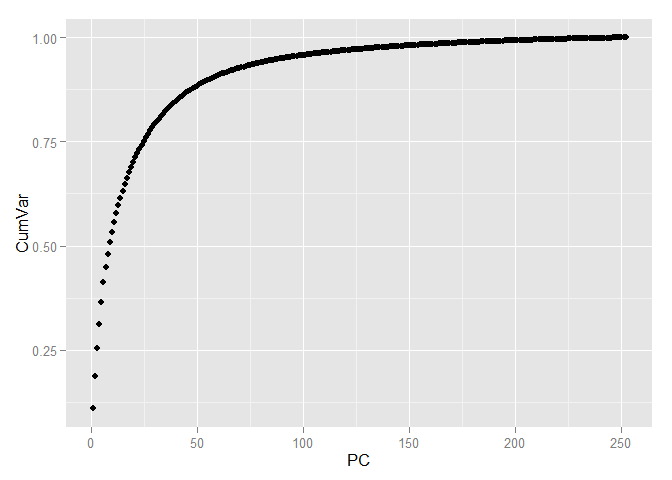
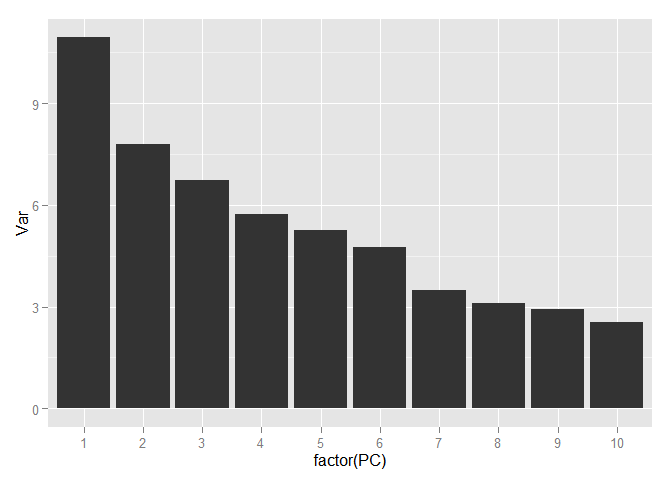
Для того, чтобы сохранить более 90 процентов информации, содержащейся в данных достаточно всего лишь 70 компонент, т.е. мы от 784 признаков пришли к 70 и, при этом, потеряли менее 10 процентов вариации данных!
Преобразуем тренировочную и тестовую выборки в пространство главных компонент.
Для выбора параметров моделей я использую пакет caret, предоставляющий возможность выполнять параллельные вычисления, используя многоядерность современных процессоров.
Теперь приступим к созданию предсказывающих моделей используя преобразованные данные. Создадим первую модель используя метод k ближайших соседей (KNN). В этой модели есть только один параметр — количество ближайших объектов, используемых для классификации объекта. Подбирать этот параметр будем с помощью десятикратной кросс-проверки (10-fold cross-validation (CV)) с разбиением выборки на 10 частей. Оценка производится на случайно отобранной части изначальных объектов. Для оценки качества моделей будем использовать метрику Accuracy, представляющий собой процент точно предсказанных классов объектов.
Теперь сократим её и получим точное значение.
Наилучший показатель модель имеет при значении параметра k равному 3. Используя это значение получим предсказание на тестовых данных. Построим Confusion Table и вычислим Accuracy.
Вторая модель — это Random Forest. У этой модели будем выбирать параметр mtry — количество используемых признаков при получении каждого из используемых в ансамбле деревьев. Для выбора наилучшего значения данного параметра пойдём тем же путём, что и ранее.
Выбираем mtry равным 4 и получаем Accuracy на тестовых данных. Замечу, что пришлось обучать модель на части от доступных тренировочных данных, т.к. для использования всех данных требуется больше оперативной памяти. Но, как показано в предыдущей работе, это не сильно повлияет на конечный результат.
И, наконец, Support Vector Machine. В этой модели будет использоваться Radial Kernel и подбираются уже два параметра: sigma (регуляризационный параметр) и C (параметр, определяющий форму ядра).
Создадим четвёртую модель, которая представляет собой ансамбль из трёх моделей, созданных ранее. Эта модель предсказывает то значение, за которое «голосует» большинство из использованных моделей.
На тестовой выборке получены следующие результаты:
Лучший показатель Accuracy имеет модель использующая метод k ближайших соседей (KNN).
Оценка моделей на сайте Kaggle приведена в следующей таблице.
И лучшие результаты здесь у SVM.
Ну и напоследок, уже из чистого любопытства, посмотрим наглядно на произведённые методом главных компонент преобразования. Для этого, во-первых получим изображение цифр в первоначальном виде.

И изображение этих же цифр, но уже после того, как мы использовали метод PCA и оставили первые 70 компонент. Получившиеся объекты принято называть eigenfaces

В следующий раз мы рассмотрим одну из задач Text Mining'а, ну а пока можете присоединиться к курсу по Практическому анализу данных — рекомендую!

Как и обещал, продолжаю публикацию разборов задач, которые я прорешал за время работы с ребятами из MLClass.ru. В этот раз мы разберем метод главных компонент на примере известной задачи распознавания цифр Digit Recognizer с платформы Kaggle. Статья будет полезна новичкам, которые еще только начинают изучать анализ данных. Кстати, еще не поздно записаться на курс Прикладной анализ данных, получив возможность максимально быстро прокачаться в данной области.
Вступление
Данная работа является естественным продолжением исследования, изучающего зависимость качества модели от размера выборки. В ней для была показана возможность уменьшения количества используемых объектов в обучающей выборке с целью получения приемлемых результатов в условиях ограниченных вычислительных ресурсов. Но, кроме количества объектов, на размер данных влияет и количество используемых признаков. Рассмотрим эту возможность на тех же данных. Используемые данные были подробно изучены в предыдущей работе, поэтому просто загрузим тренировочную выборку в R.
library(readr)
library(caret)
library(ggbiplot)
library(ggplot2)
library(dplyr)
library(rgl)
data_train <- read_csv("train.csv")
##
|================================================================================| 100% 73 MB
Как мы уже знаем данные имеют 42000 объектов и 784 признака, представляющие собой значение яркости каждого из пикселей составляющего изображение цифры. Разобъём выборку на тренировочную и тестовую в соотношении 60/40.
set.seed(111)
split <- createDataPartition(data_train$label, p = 0.6, list = FALSE)
train <- slice(data_train, split)
test <- slice(data_train, -split)
Теперь удалим признаки, имеющие константное значение.
zero_var_col <- nearZeroVar(train, saveMetrics = T)
train <- train[, !zero_var_col$nzv]
test <- test[, !zero_var_col$nzv]
dim(train)
## [1] 25201 253
В итоге осталось 253 признака.
Теория
Метод главных компонент (PCA) преобразует базовые признаки в новые, каждый из которых является линейной комбинацией изначальных таким образом, что разброс данных (то есть среднеквадратичное отклонение от среднего значения) вдоль них максимален. Метод применяется для визуализации данных и для уменьшения размерности данных (сжатия).
PCA
Для большей наглядности случайным образом отберём из тренировочной выборки 1000 объектов и изобразим их в пространстве первых двух признаков.
train_1000 <- train[sample(nrow(train), size = 1000),]
ggplot(data = train_1000, aes(x = pixel152, y = pixel153, color = factor(label))) + geom_point()

Очевидно, что объекты перемешаны и выделить среди них группы объектов принадлежащих одному классу проблематично. Проведём преобразование данных по методу главных компонент и изобразим в пространстве первых двух компонент. Замечу, что компоненты расположены в убывающем порядке в зависимости от разброса данных, который приходится вдоль них.
pc <- princomp(train_1000[, -1], cor=TRUE, scores=TRUE)
ggbiplot(pc, obs.scale = 1, var.scale = 1, groups = factor(train_1000$label),
ellipse = TRUE, circle = F, var.axes = F) +
scale_color_discrete(name = '') +
theme(legend.direction = 'horizontal', legend.position = 'top')

Очевидно, что даже в пространстве всего лишь двух признаков уже можно выделить явные группы объектов. Теперь рассмотрим те же данные, но уже в пространстве первых трёх компонент.
plot3d(pc$scores[,1:3], col= train_1000$label + 1, size = 0.7, type = "s")

Выделение различных классов ещё больше упростилось. Теперь выберем количество компонент, которое будем использовать для дальнейшей работы. Для этого посмотрим на соотношение дисперсии и количество компонент объясняющие её, но уже используя всю тренировочную выборку.
pc <- princomp(train[, -1], cor=TRUE, scores=TRUE)
variance <- pc$sdev^2/sum(pc$sdev^2)
cumvar <- cumsum(variance)
cumvar <- data.frame(PC = 1:252, CumVar = cumvar)
ggplot(data = cumvar, aes(x = PC, y = CumVar)) + geom_point()

variance <- data.frame(PC = 1:252, Var = variance*100)
ggplot(data = variance[1:10,], aes(x = factor(PC), y = Var)) + geom_bar(stat = "identity")

sum(variance$Var[1:70])
## [1] 92.69142
Для того, чтобы сохранить более 90 процентов информации, содержащейся в данных достаточно всего лишь 70 компонент, т.е. мы от 784 признаков пришли к 70 и, при этом, потеряли менее 10 процентов вариации данных!
Преобразуем тренировочную и тестовую выборки в пространство главных компонент.
train <- predict(pc) %>% cbind(train$label, .) %>% as.data.frame(.) %>% select(1:71)
colnames(train)[1]<- "label"
train$label <- as.factor(train$label)
test %<>% predict(pc, .) %>% cbind(test$label, .) %>% as.data.frame(.) %>% select(1:71)
colnames(test)[1]<- "label"
Для выбора параметров моделей я использую пакет caret, предоставляющий возможность выполнять параллельные вычисления, используя многоядерность современных процессоров.
library("doParallel")
cl <- makePSOCKcluster(2)
registerDoParallel(cl)
KNN
Теперь приступим к созданию предсказывающих моделей используя преобразованные данные. Создадим первую модель используя метод k ближайших соседей (KNN). В этой модели есть только один параметр — количество ближайших объектов, используемых для классификации объекта. Подбирать этот параметр будем с помощью десятикратной кросс-проверки (10-fold cross-validation (CV)) с разбиением выборки на 10 частей. Оценка производится на случайно отобранной части изначальных объектов. Для оценки качества моделей будем использовать метрику Accuracy, представляющий собой процент точно предсказанных классов объектов.
set.seed(111)
train_1000 <- train[sample(nrow(train), size = 1000),]
ctrl <- trainControl(method="repeatedcv",repeats = 3)
Для начала определим область поиска значений параметра.
knnFit <- train(label ~ ., data = train_1000, method = "knn", trControl = ctrl,tuneLength = 20)
knnFit
## k-Nearest Neighbors
##
## 1000 samples
## 70 predictor
## 10 classes: '0', '1', '2', '3', '4', '5', '6', '7', '8', '9'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold, repeated 3 times)
## Summary of sample sizes: 899, 901, 900, 901, 899, 899, ...
## Resampling results across tuning parameters:
##
## k Accuracy Kappa Accuracy SD Kappa SD
## 5 0.8749889 0.8608767 0.03637257 0.04047629
## 7 0.8679743 0.8530101 0.03458659 0.03853048
## 9 0.8652707 0.8500155 0.03336461 0.03713965
## 11 0.8529954 0.8363199 0.03692823 0.04114777
## 13 0.8433141 0.8255274 0.03184725 0.03548771
## 15 0.8426833 0.8248052 0.04097424 0.04568565
## 17 0.8423694 0.8244683 0.04070299 0.04540152
## 19 0.8340150 0.8151256 0.04291349 0.04788273
## 21 0.8263450 0.8065723 0.03914363 0.04369889
## 23 0.8200042 0.7995067 0.03872017 0.04320466
## 25 0.8156764 0.7946582 0.03825163 0.04269085
## 27 0.8093227 0.7875839 0.04299301 0.04799252
## 29 0.8010018 0.7783100 0.04252630 0.04747852
## 31 0.8019849 0.7794036 0.04327120 0.04827493
## 33 0.7963572 0.7731147 0.04418378 0.04930341
## 35 0.7936906 0.7701616 0.04012802 0.04478789
## 37 0.7889930 0.7649252 0.04163075 0.04644193
## 39 0.7863463 0.7619669 0.03947693 0.04404655
## 41 0.7829758 0.7582087 0.03482612 0.03889550
## 43 0.7796388 0.7544879 0.03745359 0.04179976
##
## Accuracy was used to select the optimal model using the largest value.
## The final value used for the model was k = 5.
Теперь сократим её и получим точное значение.
grid <- expand.grid(k=2:5)
knnFit <- train(label ~ ., data = train_1000, method = "knn", trControl = ctrl, tuneGrid=grid)
knnFit
## k-Nearest Neighbors
##
## 1000 samples
## 70 predictor
## 10 classes: '0', '1', '2', '3', '4', '5', '6', '7', '8', '9'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold, repeated 3 times)
## Summary of sample sizes: 900, 901, 901, 899, 901, 899, ...
## Resampling results across tuning parameters:
##
## k Accuracy Kappa Accuracy SD Kappa SD
## 2 0.8699952 0.8553199 0.03055544 0.03402108
## 3 0.8799832 0.8664399 0.02768544 0.03082014
## 4 0.8736591 0.8593777 0.02591618 0.02888557
## 5 0.8726753 0.8582703 0.02414173 0.02689738
##
## Accuracy was used to select the optimal model using the largest value.
## The final value used for the model was k = 3.
Наилучший показатель модель имеет при значении параметра k равному 3. Используя это значение получим предсказание на тестовых данных. Построим Confusion Table и вычислим Accuracy.
library(class)
prediction_knn <- knn(train, test, train$label, k=3)
table(test$label, prediction_knn)
## prediction_knn
## 0 1 2 3 4 5 6 7 8 9
## 0 1643 0 6 1 0 1 2 0 0 0
## 1 0 1861 4 1 2 0 0 0 0 0
## 2 7 7 1647 3 0 0 1 11 0 0
## 3 1 0 9 1708 2 19 4 6 1 3
## 4 0 4 0 0 1589 0 10 7 0 6
## 5 3 2 1 20 1 1474 13 0 6 2
## 6 0 0 0 1 2 3 1660 0 0 0
## 7 0 6 3 0 2 0 0 1721 0 13
## 8 0 1 0 11 1 16 12 4 1522 20
## 9 0 0 1 3 3 5 1 23 5 1672
sum(diag(table(test$label, prediction_knn)))/nrow(test)
## [1] 0.9820227
Random Forest
Вторая модель — это Random Forest. У этой модели будем выбирать параметр mtry — количество используемых признаков при получении каждого из используемых в ансамбле деревьев. Для выбора наилучшего значения данного параметра пойдём тем же путём, что и ранее.
rfFit <- train(label ~ ., data = train_1000, method = "rf", trControl = ctrl,tuneLength = 3)
rfFit
## Random Forest
##
## 1000 samples
## 70 predictor
## 10 classes: '0', '1', '2', '3', '4', '5', '6', '7', '8', '9'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold, repeated 3 times)
## Summary of sample sizes: 901, 900, 900, 899, 902, 899, ...
## Resampling results across tuning parameters:
##
## mtry Accuracy Kappa Accuracy SD Kappa SD
## 2 0.8526986 0.8358081 0.02889351 0.03226317
## 36 0.8324051 0.8133909 0.03442843 0.03836844
## 70 0.8026823 0.7802912 0.03696172 0.04118363
##
## Accuracy was used to select the optimal model using the largest value.
## The final value used for the model was mtry = 2.
grid <- expand.grid(mtry=2:6)
rfFit <- train(label ~ ., data = train_1000, method = "rf", trControl = ctrl,tuneGrid=grid)
rfFit
## Random Forest
##
## 1000 samples
## 70 predictor
## 10 classes: '0', '1', '2', '3', '4', '5', '6', '7', '8', '9'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold, repeated 3 times)
## Summary of sample sizes: 898, 900, 900, 901, 900, 898, ...
## Resampling results across tuning parameters:
##
## mtry Accuracy Kappa Accuracy SD Kappa SD
## 2 0.8553016 0.8387134 0.03556811 0.03967709
## 3 0.8615798 0.8457973 0.03102887 0.03458732
## 4 0.8669329 0.8517297 0.03306870 0.03690844
## 5 0.8739532 0.8595897 0.02957395 0.03296439
## 6 0.8696883 0.8548470 0.03203166 0.03568138
##
## Accuracy was used to select the optimal model using the largest value.
## The final value used for the model was mtry = 5.
Выбираем mtry равным 4 и получаем Accuracy на тестовых данных. Замечу, что пришлось обучать модель на части от доступных тренировочных данных, т.к. для использования всех данных требуется больше оперативной памяти. Но, как показано в предыдущей работе, это не сильно повлияет на конечный результат.
library(randomForest)
rfFit <- randomForest(label ~ ., data = train[sample(nrow(train), size = 15000),], mtry = 4)
prediction_rf<-predict(rfFit,test)
table(test$label, prediction_rf)
## prediction_rf
## 0 1 2 3 4 5 6 7 8 9
## 0 1608 0 6 3 4 1 20 2 9 0
## 1 0 1828 9 9 3 5 3 2 9 0
## 2 12 9 1562 16 15 5 6 19 31 1
## 3 12 1 26 1625 2 33 12 14 22 6
## 4 0 6 11 1 1524 0 22 7 6 39
## 5 12 3 3 48 12 1415 10 1 15 3
## 6 13 4 8 0 4 11 1623 0 3 0
## 7 3 14 25 2 13 3 0 1653 4 28
## 8 4 10 12 64 8 21 12 5 1428 23
## 9 4 4 10 39 38 10 0 39 7 1562
sum(diag(table(test$label, prediction_rf)))/nrow(test)
## [1] 0.9421989
SVM
И, наконец, Support Vector Machine. В этой модели будет использоваться Radial Kernel и подбираются уже два параметра: sigma (регуляризационный параметр) и C (параметр, определяющий форму ядра).
svmFit <- train(label ~ ., data = train_1000, method = "svmRadial", trControl = ctrl,tuneLength = 5)
svmFit
## Support Vector Machines with Radial Basis Function Kernel
##
## 1000 samples
## 70 predictor
## 10 classes: '0', '1', '2', '3', '4', '5', '6', '7', '8', '9'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold, repeated 3 times)
## Summary of sample sizes: 901, 900, 898, 900, 900, 901, ...
## Resampling results across tuning parameters:
##
## C Accuracy Kappa Accuracy SD Kappa SD
## 0.25 0.7862419 0.7612933 0.02209354 0.02469667
## 0.50 0.8545924 0.8381166 0.02931921 0.03262332
## 1.00 0.8826064 0.8694079 0.02903226 0.03225475
## 2.00 0.8929180 0.8808766 0.02781461 0.03090255
## 4.00 0.8986322 0.8872208 0.02607149 0.02898200
##
## Tuning parameter 'sigma' was held constant at a value of 0.007650572
## Accuracy was used to select the optimal model using the largest value.
## The final values used for the model were sigma = 0.007650572 and C = 4.
grid <- expand.grid(C = 4:6, sigma = seq(0.006, 0.009, 0.001))
svmFit <- train(label ~ ., data = train_1000, method = "svmRadial", trControl = ctrl,tuneGrid=grid)
svmFit
## Support Vector Machines with Radial Basis Function Kernel
##
## 1000 samples
## 70 predictor
## 10 classes: '0', '1', '2', '3', '4', '5', '6', '7', '8', '9'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold, repeated 3 times)
## Summary of sample sizes: 901, 900, 900, 899, 901, 901, ...
## Resampling results across tuning parameters:
##
## C sigma Accuracy Kappa Accuracy SD Kappa SD
## 4 0.006 0.8943835 0.8824894 0.02999785 0.03335171
## 4 0.007 0.8970537 0.8854531 0.02873482 0.03194698
## 4 0.008 0.8984139 0.8869749 0.03068411 0.03410783
## 4 0.009 0.8990838 0.8877269 0.03122154 0.03469947
## 5 0.006 0.8960834 0.8843721 0.03061547 0.03404636
## 5 0.007 0.8960703 0.8843617 0.03069610 0.03412880
## 5 0.008 0.8990774 0.8877134 0.03083329 0.03427321
## 5 0.009 0.8990838 0.8877271 0.03122154 0.03469983
## 6 0.006 0.8957534 0.8840045 0.03094360 0.03441242
## 6 0.007 0.8963971 0.8847267 0.03081294 0.03425451
## 6 0.008 0.8990774 0.8877134 0.03083329 0.03427321
## 6 0.009 0.8990838 0.8877271 0.03122154 0.03469983
##
## Accuracy was used to select the optimal model using the largest value.
## The final values used for the model were sigma = 0.009 and C = 4.
library(kernlab)
svmFit <- ksvm(label ~ ., data = train,type="C-svc",kernel="rbfdot",kpar=list(sigma=0.008),C=4)
prediction_svm <- predict(svmFit, newdata = test)
table(test$label, prediction_svm)
## prediction_svm
## 0 1 2 3 4 5 6 7 8 9
## 0 1625 0 5 1 0 3 13 0 6 0
## 1 1 1841 6 6 4 1 0 3 5 1
## 2 8 4 1624 5 7 1 1 13 11 2
## 3 2 0 18 1684 0 23 2 6 12 6
## 4 1 3 3 0 1567 0 9 7 5 21
## 5 8 3 2 24 6 1465 7 0 6 1
## 6 2 1 2 1 5 5 1649 0 1 0
## 7 3 8 15 3 3 0 0 1695 3 15
## 8 1 6 10 10 5 9 3 4 1530 9
## 9 3 1 5 13 14 9 0 21 3 1644
sum(diag(table(test$label, prediction_svm)))/nrow(test)
## [1] 0.9717245
Ансамбль моделей
Создадим четвёртую модель, которая представляет собой ансамбль из трёх моделей, созданных ранее. Эта модель предсказывает то значение, за которое «голосует» большинство из использованных моделей.
all_prediction <- cbind(as.numeric(levels(prediction_knn))[prediction_knn],
as.numeric(levels(prediction_rf))[prediction_rf],
as.numeric(levels(prediction_svm))[prediction_svm])
predictions_ensemble <- apply(all_prediction, 1, function(row) {
row %>% table(.) %>% which.max(.) %>% names(.) %>% as.numeric(.)
})
table(test$label, predictions_ensemble)
## predictions_ensemble
## 0 1 2 3 4 5 6 7 8 9
## 0 1636 0 5 1 0 1 8 0 2 0
## 1 1 1851 3 5 3 0 0 1 4 0
## 2 7 6 1636 3 6 0 0 11 7 0
## 3 6 0 14 1690 1 18 4 8 7 5
## 4 0 5 4 0 1573 0 12 6 2 14
## 5 5 1 2 21 5 1478 7 0 3 0
## 6 3 1 2 0 5 3 1651 0 1 0
## 7 1 11 12 2 1 0 0 1704 0 14
## 8 1 5 11 17 4 13 4 3 1514 15
## 9 4 2 4 21 11 5 0 20 1 1645
sum(diag(table(test$label, predictions_ensemble)))/nrow(test)
## [1] 0.974939
Итоги
На тестовой выборке получены следующие результаты:
| Model | Test Accuracy |
| KNN | 0.981 |
| Random Forest | 0.948 |
| SVM | 0.971 |
| Ensemble | 0.974 |
Лучший показатель Accuracy имеет модель использующая метод k ближайших соседей (KNN).
Оценка моделей на сайте Kaggle приведена в следующей таблице.
| Model | Kaggle Accuracy |
| KNN | 0.97171 |
| Random Forest | 0.93286 |
| SVM | 0.97786 |
| Ensemble | 0.97471 |
И лучшие результаты здесь у SVM.
Eigenfaces
Ну и напоследок, уже из чистого любопытства, посмотрим наглядно на произведённые методом главных компонент преобразования. Для этого, во-первых получим изображение цифр в первоначальном виде.
set.seed(100)
train_1000 <- data_train[sample(nrow(data_train), size = 1000),]
colors<-c('white','black')
cus_col<-colorRampPalette(colors=colors)
default_par <- par()
number_row <- 28
number_col <- 28
par(mfrow=c(5,5),pty='s',mar=c(1,1,1,1),xaxt='n',yaxt='n')
for(i in 1:25)
{
z<-array(as.matrix(train_1000)[i,-1],dim=c(number_row,number_col))
z<-z[,number_col:1]
image(1:number_row,1:number_col,z,main=train_1000[i,1],col=cus_col(256))
}
par(default_par)

И изображение этих же цифр, но уже после того, как мы использовали метод PCA и оставили первые 70 компонент. Получившиеся объекты принято называть eigenfaces
zero_var_col <- nearZeroVar(train_1000, saveMetrics = T)
train_1000_cut <- train_1000[, !zero_var_col$nzv]
pca <- prcomp(train_1000_cut[, -1], center = TRUE, scale = TRUE)
restr <- pca$x[,1:70] %*% t(pca$rotation[,1:70])
restr <- scale(restr, center = FALSE , scale=1/pca$scale)
restr <- scale(restr, center = -1 * pca$center, scale=FALSE)
restr <- as.data.frame(cbind(train_1000_cut$label, restr))
test <- data.frame(matrix(NA, nrow = 1000, ncol = ncol(train_1000)))
zero_col_number <- 1
for (i in 1:ncol(train_1000)) {
if (zero_var_col$nzv[i] == F) {
test[, i] <- restr[, zero_col_number]
zero_col_number <- zero_col_number + 1
}
else test[, i] <- train_1000[, i]
}
par(mfrow=c(5,5),pty='s',mar=c(1,1,1,1),xaxt='n',yaxt='n')
for(i in 1:25)
{
z<-array(as.matrix(test)[i,-1],dim=c(number_row,number_col))
z<-z[,number_col:1]
image(1:number_row,1:number_col,z,main=test[i,1],col=cus_col(256))
}
par(default_par)

В следующий раз мы рассмотрим одну из задач Text Mining'а, ну а пока можете присоединиться к курсу по Практическому анализу данных — рекомендую!
Комментарии (5)

netmaxed
18.09.2015 08:43Насколько я понимаю, eigenfaces взялось из примеров с обработкой лиц — в PCA считаются собственные значения и вектора и полученные вектора, представленные как картинки и называли eigenfaces. Так что у вас eigendigits скорее.


hellman
А есть картинки цифр которые не распознались?
GMorozov
Пожалуйста. Над изображениями те цифры, которые им присвоила модель.

potan
В третьей и в последней картинке я согласен с компьютером.
ciiccii
А можно код, как получить неправильно распознаные цифры?