Статистически устойчивый анализ данных. Тест Флигнера-Киллина / forpes.ru

Главная
Статистически устойчивый анализ данных. Тест Флигнера-Киллина

Статистически устойчивый анализ данных. Тест Флигнера-Киллина +1

30.03.2021 23:26

ampopov 0 826 Источник

1. Наряду с проверкой различия параметров положения двух генеральных совокупностей часто требуется проверить различие двух параметров масштаба.

Пусть $X_1,\ldots,X_{n_1}$ – случайная выборка объёма n_1 с плотностью распределения $f[(x-\theta_1)/\sigma_1]$ и $Y_1,\ldots,Y_{n_2}$ – случайная выборка объёма n_2 с плотностью распределения $f[(y-\theta_2)/\sigma_2]$ , где f(x) – симметричная функция плотности распределения случайной величины, $\sigma_1,\sigma_2>0$ .

Отметим, что в оговоренных условиях, имеем

$\frac{X-\theta_1}{\sigma_1}=\frac{Y-\theta_2}{\sigma_2},$

откуда, в частности, следует

$\Delta=\ln|X-\theta_1|-\ln|Y-\theta_2|=\ln\left(\frac{\sigma_1}{\sigma_2}\right)=\ln\eta.$

2. Интересующая нас гипотеза имеет вид

$H_0:\eta=1,~~~H_a:\eta\neq1,$

где $\eta=\sigma_1/\sigma_2$ . Далее рассматривается, основанная на рангах, процедура для проверки указанной гипотезы – тест Флигнера-Киллина (Fligner-Killeen test), а также строятся точечная оценка и доверительный интервал для параметра $\eta$ .

3. Так как тест для проверки гипотезы H_0 должен не зависеть от параметров положения, то следует центрировать имеющиеся наблюдения. В параметрическом F-тесте (var.test {stats}), основанном на отношении выборочных дисперсий, для этой цели используются выборочные средние; вместо них мы применим, равные им в силу симметрии f(x) , медианы:

$\begin{array}{ll}X_i^*=X_i-\mbox{med}\{X_i\},&i=1,\ldots,n_1,\\Y_j^*=Y_j-\mbox{med}\{Y_j\},&j=1,\ldots,n_2.\end{array}$

Исключив из дальнейшего рассмотрения возможные нулевые значения, найдём логарифмы абсолютных величин центрированных наблюдений. В результате получим две выборки $\ln|X_1^*|,\ldots,\ln|X_{n_1}^*|$ и $\ln|Y_1^*|,\ldots,\ln|Y_{n_2}^*|$ , разница в параметрах положения которых (ключевой момент!) равна $\Delta=\ln\eta$ .

Таким образом, задача о различии параметров масштаба сведена к задаче о различии параметров положения. Применим для её решения анализ, основанный на score функциях, разбор которого начат в предшествующей статье «Статистически устойчивый анализ данных: тест Манна-Уитни-Уилкоксона и Score-функции».

4. Так как логарифмическая функция монотонно возрастает, то ранги исходных наблюдений и ранги их логарифмов совпадают. Это позволяет сформировать следующую статистику

$S_\varphi(0)=\sum_{j=1}^{n_2}a_\varphi[R(\ln|Y_j^*|)]=\sum_{j=1}^{n_2}a_\varphi[R(|Y_j^*|)],$

где ранги рассчитываются по объединенной выборке. Данная статистика может быть использована для проверки исследуемой нулевой гипотезы H_0 о величине параметра $\eta$ [см. пункты 6, 7 прошлой статьи].

Напомним, что в условиях нулевой гипотезы распределение статистики $S_\varphi(0)$ асимптотически нормально, с нулевым математическим ожиданием $E_{H_0}[S_\varphi(0)]=0$ и дисперсией

$\sigma_\varphi^2=Var_{H_0}[S_\varphi(0)]=\frac{n_1n_2}{n(n-1)}\sum_{i=1}^na_\varphi^2(i).$

Это позволяет использовать стандартизованную статистику

$z_\varphi=\frac{S_\varphi(0)}{\sigma_\varphi}$

чтобы отвергнуть гипотезу H_0 на уровне значимости $\alpha$ , если $z_\varphi\geq z_\alpha$ , где $z_\alpha$ – квантиль уровня $(1-\alpha)$ стандартного нормального распределения.

Решение вопроса о том, какую score функцию использовать при расчете статистики $S_\varphi(0)$ зависит от вида функции f(x) . В распространенном случае, когда f(x) имеет нормальное распределение, оптимальной является квадратичная нормальная score функция (squared-normal score) вида

$\varphi_{FK}=\left(\Phi^{-1}\left(\frac{u+1}{2}\right)\right)^2-1,$

где $\Phi$ – cdf стандартного нормального распределения, FK – аббревиатура, соответствующая работе Fligner и Killeen (1976) [1], где данная функция была предложена.

5. Для демонстрации изложенной выше методики рассмотрим данные конкретного эксперимента (Doksum and Sievers (1976) [2]) о влиянии озона на прирост в весе у крыс. Контрольная группа крыс (n_1=23) в течениедней находилась в обычной среде, в то время как экспериментальная группа крыс (n_2=22) в течение 7 дней находилась в среде с повышенной концентрацией озона. В конце недели изменение в весе каждой крысы были взяты в качестве отклика.

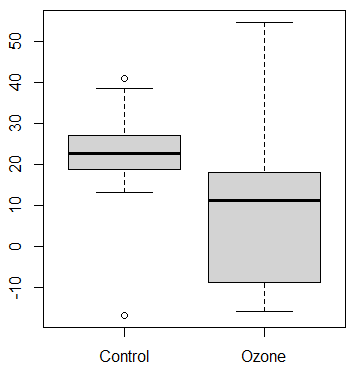
Следующая программа на зыке R содержит алгоритм расчета статистики $z_{FK}$ и соответствующего значения p-value для проверки двухсторонней гипотезы о различии параметров масштаба двух выборок.

> x <-
+   c(
+     41.0,    38.4,    24.4,    25.9,    21.9,
+     18.3,    13.1,    27.3,    28.5,   -16.9,
+     26.0,    17.4,    21.8,    15.4,    27.4,
+     19.2,    22.4,    17.7,    26.0,    29.4,
+     21.4,    26.6,    22.7)
> y <-
+   c(
+     10.1,     6.1,    20.4,     7.3,    14.3,
+     15.5,    -9.9,     6.8,    28.2,    17.9,
+     -9.0,  - 12.9,    14.0,     6.6,    12.1,
+     15.7,    39.9,   -15.9,    54.6,   -14.7,
+     44.1,    -9.0)
> 
> # Зададим squared-normal score функцию
>   fkscores = new(
+     "scores",
+     phi = function(u) {
+       (qnorm((u + 1) / 2)) ^ 2 - 1
+     },
+     Dphi = function(u) {
+       qnorm((u + 1) / 2) / dnorm(qnorm((u + 1) / 2))
+     }
+   )
> # Проверим гипотезу о равенстве 0 параметра Delta
>   zed = c(abs(x - median(x)), abs(y - median(y)))
>   n1 = length(x)
>   n2 = length(y)
>   n = n1 + n2
> 
> # В расчётe используется стандартизированная score функция
>   rz = rank(zed)/(n + 1)
>   afk = Rfit::getScores(fkscores, rz)
> 
> # Расчет статистики Sfk, zfk, p-value
>   Sfk = sum(afk[(n1+1):n])
> 
>   varfk = ((n1 * n2)/(n*(n-1))) * sum(afk^2)
>   zfk = Sfk/sqrt(varfk)
>   see = "two.sided"
>   if (see == "two.sided") {
+     pvalue = 2 * (1 - pnorm(abs(zfk)))
+   }
>   if (see == "greater") {
+     pvalue = 1 - pnorm(zfk)
+   }
>   if (see == "less") {
+     pvalue = pnorm(zfk)
+   }
> 
> # Вывод результатов
>   res <- list(statistic = zfk, p.value = pvalue)
>   with(res, cat("statistic = ", statistic, ", p-value = ", p.value, "\n"))

statistic =  2.095976 , p-value =  0.03608434

Стандартизованная статистика теста Флигнера-Киллина имеет значение $z_{FK}=2.095$ c p-value 0.036 , то есть можно сказать, что наличие озона влияет на вариабельность в приросте веса у крыс.

6. Для того чтобы получить точечную оценку и доверительный интервал для параметра $\eta$ сформулируем нашу задачу в виде лог-модели. Пусть

$Z_i=\left\{\begin{array}{ll}\ln|X_i^*|&i=1,\ldots,n_1,\\\ln|Y_{i-n_1}^*|&i=n_1+1,\ldots,n_1+n_2.\end{array}\right.$

$\bar{c}$ – вектор-индикатор, с первыми n_1 элементами равными нулю и последними n_2 элементами равными единице. Тогда регрессионная задача [см. пункт 8 прошлой статьи] имеет вид

$Z_i=\Delta c_i+e_i,~~~i=1,2,\ldots,n.$

Применяя алгоритм построения ранговой регрессии (rfit {Rfit}) с использованием квадратичной нормальной score функций $\varphi_{FK}$ можно найти оценку $\hat{\Delta}_{FK}$ параметра $\Delta$ . Откуда оценка для параметра $\eta$ получается в виде $\hat{\eta}_{FK}=\exp\{\hat{\Delta}_{FK}\}$ .

Далее, используя найденную в ходе построения регрессии величину стандартной ошибки $\mbox{SE}(\hat{\Delta}_{FK})$ , можно построить, например, приблизительный $95\%$ доверительный интервал для $\Delta$ , основанный на квантиле уровня $1-\alpha/2$ t-распределения с n'-2 степенями свободы

$L_{FK}=\hat{\Delta}_{FK}-t_{\alpha/2,n'-2}\cdot\mbox{SE}(\hat{\Delta}_{FK}),~~~U_{FK}=\hat{\Delta}_{FK}+t_{\alpha/2,n'-2}\cdot\mbox{SE}(\hat{\Delta}_{FK}),$

где– объем выборки Z_i , $0<\alpha<1$ . Рассчитанные границы также преобразуются в соответствующие границы доверительного интервала для $\eta$ : $(\exp\{L_{FK}\},\exp\{U_{FK}\})$ . Отметим, что найденные таким образом доверительные границы всегда положительны.

7. Следующая программа на языке R содержит алгоритм расчета точечной оценки и доверительного интервала для параметра $\eta$ .

> # Подготовим данные   
>   xs = abs(x - median(x))
>   xs = xs[xs != 0]
>   xstarl = log(xs)
>   ys = abs(y - median(y))
>   ys = ys[ys != 0]
>   ystarl = log(ys)
>   n1s = length(xs)
>   n2s = length(ys)
>   ns = n1s + n2s
> 
> # Построим уравнение регрессии
>   cvec = c(rep(0, n1s), rep(1, n2s))
>   zed = c(xstarl, ystarl)
>   fitz = rfit(zed ~ cvec, scores = fkscores)
>   (sumf = summary(fitz))

Call:
rfit.default(formula = zed ~ cvec, scores = fkscores)

Coefficients:
            Estimate Std. Error t.value   p.value    
(Intercept)  1.42288    0.38905  3.6573 0.0007044 ***
cvec         0.86586    0.42783  2.0238 0.0493802 *  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Multiple R-squared (Robust): 0.07815811 
Reduction in Dispersion Test: 3.56096 p-value: 0.06608 

>   delta = coef(sumf)[2, 1]
> 
> # Оценка отношения параметров масштаба
>   (eta = exp(delta))

[1] 2.377049
> 
> # Построим доверительный интервал
>   conf.level = 0.95
>   se = coef(sumf)[2, 2]
>   tc = abs(qt(((1 - conf.level)/2), ns - 2))
>   lb = delta - tc * se
>   ub = delta + tc * se
>   conf.int = c(exp(lb), exp(ub))
>   cat(100 * conf.level, " percent confidence interval:\n", conf.int)

95  percent confidence interval:
 1.002462 5.636488

Таким образом, ранговая оценка параметра $\eta$ равна 2.337 c $95\%$ доверительным интервалом (1.002,5.636) . Это также подтверждает вывод о том, что нулевую гипотезу H_0 о равенстве параметров масштаба следует отвергнуть.

8. В заключение отметим, что рассматриваемая в статье ранговая процедура на основе предложенной Флигнером и Киллингом квадратичной нормальной score функции позволяет успешно проверять гипотезы о различии параметров масштаба, в двух важных случаях:

когда плотность распределение функции ошибкисимметрична, то есть процедура обобщает чувствительный к отклонениям от нормальности F-критерий;
когда распределение генеральной совокупности относится к классу засорённых нормальных распределений (skewed contaminated normal distributions). В этом случае случайная величина получается по закону $X=X_1\cdot(1-I_\epsilon)+I_\epsilon\cdot X_2$ , гдеиимеюти $N(\mu_c,\sigma_c^2)$ распределения соответственно, $I_\epsilon$ – имеет распределение Бернулли с вероятностью успеха $\epsilon$ и,и $I_\epsilon$ независимы в совокупности.

Ссылки на литературу:

Fligner, M. A. and Killeen, T. J. (1976), Distribution-free two-sample test for scale, Journal of the American Statistical Association, 71, 210-213.
Doksum, K. A. and Sievers, G. L. (1976), Plotting with confidence: Graphical comparisons of two populations, Biometrika, 63, 421-434.

Статистически устойчивый анализ данных. Тест Флигнера-Киллина +1

Комментарии (0)