7-сегментный индикатор
7-сегментный индикатор - один из самых популярных и простых видов отображение арабских цифр и других символов. Запатентованный еще в 1910 Фрэнком Вудом, он остается востребованным и по сей день.

Так как чаще всего в подобных индикаторах используются светодиоды, а как известно у них есть катод и анод, следовательно, и сами дисплеи делятся на 2 подтипа: с общим катодом и с общим анодом. Отличия минимальные, но иногда есть случаи, когда есть один более приоритетный вариант.
Индикатор представляет собой набор светодиодов с объединенным либо анодом, либо катодом, в зависимости от типа. Как мы можем заметить, можно управлять каждым сегментом в отдельности.
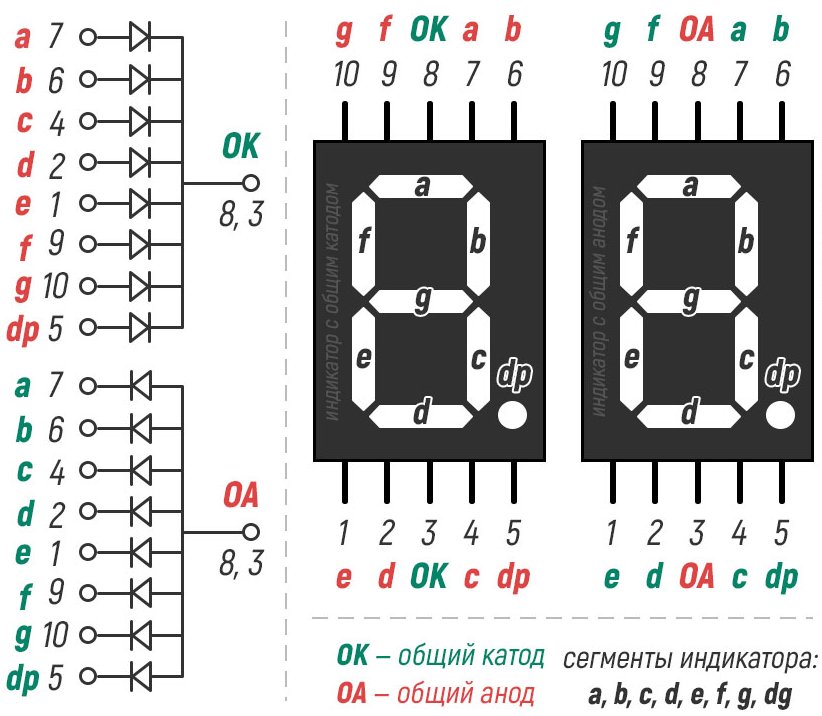
Допустим, для примера мы возьмем дисплей с общим катодом. Давайте попробуем вывести несколько цифр на дисплей. Для начала возьмем 0; для того, чтобы вывести нам надо подключить пины 7, 6, 4, 2, 1, 9 (a, b, c, d, e, f - соответственно) к "+" питания, и не забываем про резисторы, чтобы светодиоды не перегорели; если вы используете питание 5V, то будет достаточно подключить резистор на 330Ohm от пина 3, 8 к GND. И вот, на индикаторе можно наблюдать 0. Также можно вывести 1; подключаем пины 6, 4 (b, c) к положительному контакту питания и можно видим единичку на дисплее. Остальные цифры выводятся аналогично.

Возникающие проблемы
Мы разобрались, как можно выводить различные символы на индикатор, но представим, что у нас есть какое-то электронное устройство, которое должно считать числа, и для удобства мы хотим использовать индикатор, но вот незадача, у нас осталось всего 4 свободных I/0 линии, или мы намеренно хотим это оптимизировать, чтобы не писать код на микроконтроллере для представления цифр на экране или более удобным для нас способом. Напомню, при простом подключении необходимо 8 таких линий.
Кодирование
Так как самая привычная для нас система счисления это десятичная, то будем использовать ее и цифры от 0 до 9. При желании также можно продолжить и для 16-ричной системы. Поскольку у нас все строится пока что на 5V логике, то было бы странно не использовать двоичную систему счисления. У нас есть 10 цифр, следовательно, нам нужно минимум 4 бита для представления всех возможных вариантов. Для удобства предлагаю сделать таблицу.
Decimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Binary | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 |
Представим, что у нас есть 4-bit шина, по которой наше устройство передает сигнал в двоичном представлении. Теперь надо декодировать и передать его на дисплей.
Декодирование
Использование двоичной системы счисления, предпологает использование булевой логики. Поэтому будет целесообразно использовать ее. Поэтому для начала мы сделаем таблицу истинности для декодера.

Пока что мы будем использовать простую шину из 4 проводов, по каждому из которых будет передаваться сигнал. В нашем случае 5V - логическая единица, а GND - логический нуль. В таблице первый столбец только для ясности, какую цифру мы хотим отобразить. Исходя из этой таблицы нам надо создать устройство, которое при входных значениях в шине, на выходе выдавало бы 7 значений для индикатора. Для этого, мы будем использовать операции над булевыми значениями: конъюнкция (и, &), дизъюнкция (или, |), отрицание (не, ¬). Итак, приступим к созданию цепи логических вентилей.
Цепь для сегмента 'а'
Из таблицы истинности видно, что сегмент а должен быть включен всегда, кроме цифры 1 и 4. Для упрощения можно сделать так, чтобы логическая единица была только в этих 2 состояниях, и на выход добавить логическое НЕ. Тогда у нас всегда будет 1, кроме 2-ух состояний. Вот схема:

Я добавил дополнительную инвертированную шину для удобства и наглядности.
На выходе должен быть логический 0 при входных значениях 0 0 0 1 и 0 1 0 0 (на линиях 3, 2, 1, 0 соответственно). Поэтому я взял не инвертированную первую линию, а все остальные инвертированные, и получилось, что 0 0 0 1 трансформируется в 1' 1' 1' 1 ( ' - инвертированный сигнал), после все эти сигналы группируются в один общий, который идет в вентиль ИЛИ-НЕ, который на конце и инвертирует логическую 1 в 0, чтобы при этих входных параметрах сегмент а не был включен. То же самое проделывается для другого случая: 0 1 0 0 преобразуется в 1' 1 1' 1' и также идет в тот же вентиль ИЛИ-НЕ, как и при первом случае.
По такой схеме делаются остальные модули для других сегментов индикатора. В итоге у вас должно получиться нечто подобное:

Улучшение
Данная схема полностью рабочая, но в ней много повторяющихся элементов, и она будет занимать слишком много места, даже если делать отдельную интегральную схему. Поэтому ее стоит доработать.
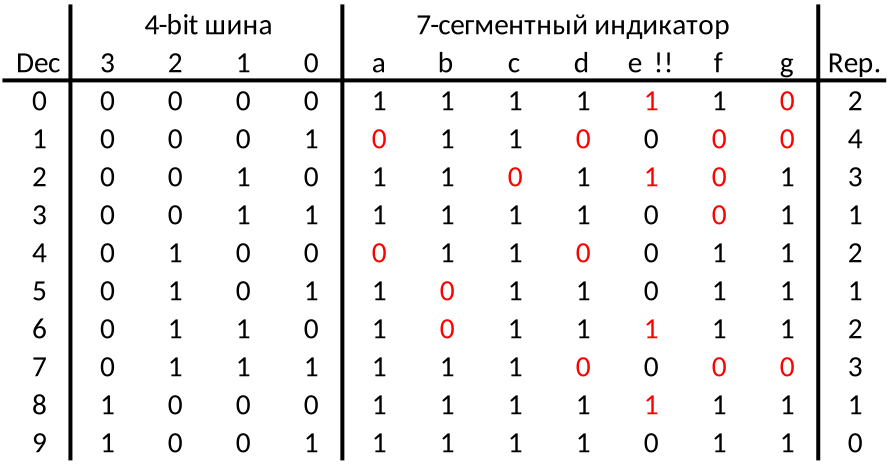
Для начала, взглянем на таблицу истинности. Можно заметить, что для сегмента е больше логических 0, так что для него, можно не инвертировать выход (!! - двойное отрицание, то есть ничего не меняем). Также использование одного и того же модуля для цифры 1 происходит 4 раза! А для цифры 9 можно не делать модуль вообще (количество повторений одного модуля для цифры вынесено в последнюю колонку). Это существенная трата пространства и логических вентилей. После реинжинеринга, на выходе будет примерно такая схема:

Реализация
Есть три способа воплотить данный декодер в жизнь.
Из готовых микросхем логических вентилей, например серия микросхем 74HCxx. Данный способ самый простой, не самый практичный, но вполне допустимый. Также его будет просто модернизировать для n-разярдных индикаторов. И отлично подходит для тестов.
Более сложный, но более "крутой" способ, создание всех логических вентилей на ТТЛ, отлично подойдут транзисторы BC546 и его комплементарная пара BC556. Этот способ потребует дополнительного создания схемы на транзисторах, для их корректной работы. Будет занимать больше пространства, но можно сделать прозрачный корпус и поставить на полочку. Ведь применение ТТЛ в наше время, дело совсем незаурядное.
Промышленный способ - изготовление полноценных кремниевых интегральных схем. Этот способ не самый быстрый, но позволяет наладить массовое производство. НО стоит отметить, что уже давно выпускаются подобные микросхемы, и это будет не слишком целесообразно.
Эпилог
В конце, хотелось отметить, что данный декодер являются не плохой практической работой для тренировки создания логических схем и для понимаю как устроенные простые электронные устройства. Идейным вдохновителем для создания данного исследования стал Ben Eater.



vadimr
В этом деле не всё так просто, потому что при смене цифр на параллельной шине будут возникать промежуточные состояния и, как следствие, могут мигать лишние сегменты (например, при переходе от 1 к 2 будет некрасиво выглядеть мигание сегмента f, если второй разряд будет не поспевать за первым и на шине будет кратковременно образовываться 0). Также и длина пути до разных сегментов разная, что не очень хорошо. Как упражнение в минимизации булевых функций описанное нормально, но в реальной жизни желательно всё-таки стробирование данных.
N1X
Как по мне — для начинающих как раз хорошо показана суть. А остальное — это уже для второго урока :)
Tiriet
В статье описана попытка минимизации булевых функций, и ни слова не сказано о нормальных формах, СДНФ, СКНФ и картах Карно. Куда после это статьи читать начинающему? Какая суть показана?
Tiriet
В тегах стоит схемотехника. Оптимизация булевых функций в ней проработана- до 5ти термов оптимизируются на картах Карно вручную матаматически строго. Где это все?
Tiriet
Для сегмента «а» таблица для карт Карно имеет вид
x1=0 x1=1 x1=1 x1=0
x0=0 x0=0 x0=1 x0=1
x3=0 x2=0| 1 1 1 0
x3=1 x2=0| 1 x x 1
x3=1 x2=1| x x x x
x3=0 x2=1| 0 1 1 1
где x- факультативные значения (не заданы в целевой функции, и могут быть выбраны нами по произволу)
давайте возьмем их такими:
x1=0| x1=1 x1=1 x1=0
x0=0| x0=0 x0=1 x0=1
x3=0 x2=0| 1 1 1 0
x3=1 x2=0| 1 1 1 1
x3=1 x2=1| 1 1 1 1
x3=0 x2=1| 0 1 1 1
тогда видим, что в центре у нас большой крестик, образованный пересчением столбца с X1=1 и строки с Х3=1, в котором все значения целевой функции равны 1. то есть, наша итоговая функция имеет вид X1 or X3 or Something. оставшиеся вне крестика две единички тоже можно объединить с соседними
x1=0 x1=1 x1=1 x1=0
x0=0 x0=0 x0=1 x0=1
x3=0 x2=0| 1 1 1 0
x3=1 x2=0| 1 1 1 1
x3=1 x2=1| 1 1 1 1
x3=0 x2=1| 0 1 1 1
и тогда для нашего Something получается выражение
(!x2 and !x0) or (x2 and x0)
в итоге для нашего сегмента получаем вот такую логическую функцию:
a = X1 or X3 or (!x2 and !x0) or (x2 and x0).
Вся фишка карт Карно в том, что любые две соседние ячейки отличаются только в одном терме (бите), и если в двух соседних ячейках находится одинаковое значение- то от соответствующего переменного бита ничего не зависит и он для данных значений может быть исключен. А если есть две соседних пары таких парных ячеек- то исключается еще один бит, и так далее. И для совсем одаренных можно составить трафаретики из картона, которые можно просто накладывать на таблицу истинности логической функции, и если в трафаретике видны только единички (или только нули)- то сразу видно, во что сворачивается покрытая трафаретом область. но если термов 5 или более- то уже нарисовать такую красивую карту, как в рассмотренном случае- нельзя, нужно рисовать или в трех измерениях, или раскидывать как-то, и метод становится сложно применим.
MrZloHex Автор
спасибо конечно, в том, что дали удостоверится в моих расщетах. Я хотел рассказать как я делал декодер, но в статью решил не включать карты Карно, решив, что стоит продолжить в следуйщей статье.