Очень часто авторы алгоритмических задач делают ход конём: они берут задачу с простыми формулировками, заменяют их сложными и непонятными эквивалентами и выдают вам «сложную» задачу. В этом посте мы разберём пример одной такой задачи и обсудим пару полезных для её решения приёмов. Задача будет про палиндром.

Продолжение под катом.
Палиндромом называется строка, которая одинаково читается как слева направо, так и справа налево. Например, слово «АТАТА» — это палиндром, а вот слово «АЙАЙАЙ» — нет.

Пример палиндрома из латинских слов: он составлен таким образом, что в каком бы направлении вы ни начали читать текст, получится одно и то же
Известный кинематографический палиндром — название вышедшего в 2020 году фильма «Довод» (англ. «Tenet»). Русская адаптация в каком-то плане уникальна, потому что у нас нашлась подходящая альтернатива слову «tenet», которая тоже является палиндромом. На многих других языках (в том числе славянских) название фильма оставили как есть. Например, на украинском это «ТЕНЕТ» (Википедия).
Итак, задача. Подготовьтесь морально.
Вот несколько примеров нечётных палиндромов: «ATATA», «KKKKKKKK», «ABA», «ZO».
Рассмотрим подробнее первую строку — АТАТА. Выпишем все её подстроки нечётной длины:
В слове ZO нет подстрок нечётной длины больше чем в одну букву. И «Z», и «O» — палиндромы, поэтому «ZO» — нечётный палиндром.
Пусть нам дана строка ABCDEF, и мы можем заменить не более одного символа (K=1), чтобы сделать из неё нечётный палиндром. Оптимальным решением было бы, например, заменить первую букву на C, тогда мы получили бы CBCDEF, где длина наибольшей подстроки, являющейся нечётным палиндромом, была бы равна трём (это CBC).
С тем же успехом мы могли бы прийти к варианту ABCFEF.
А вот если изначально у нас была строка ZXXXZ, и опять можно изменить не более одного символа, то надо заменить средний, так как ZXX и XXZ не являются палиндромами. В итоге мы получим ZXZXZ.
Теперь заметим кое-что в рассмотренных примерах. Все нечётные палиндромы имеют схожую структуру: в них чередуются буквы (или все буквы одинаковые). И это действительно единственная форма, которую имеет нечётный палиндром. Почему это так?
Посмотрим ещё раз на определение: нечётным палиндромом будем называть такую строку, у которой все подстроки нечётной длины являются палиндромами. Если все подстроки нечётной длины являются палиндромами, то и все подстроки длины 3 являются палиндромами. Отсюда сразу же следует, что на чётных позициях не может быть двух различных букв, то же самое верно для нечётных.
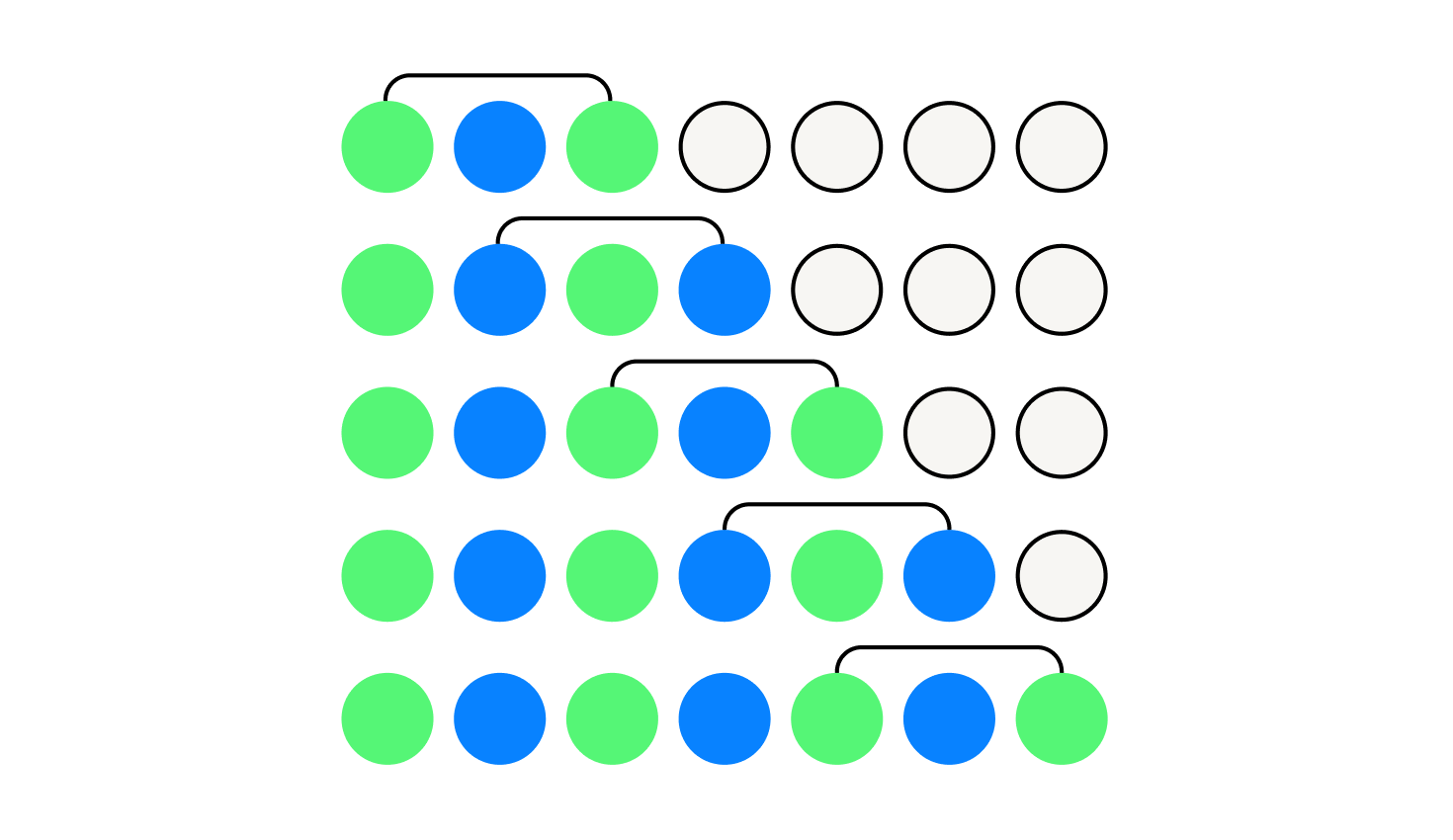
На рисунке выше показано, как получается чередующаяся структура строки. Одинаковым цветом выделены одинаковые символы. Сначала посмотрим на палиндром длины 3, который начинается в самом первом символе исходной строки. Тогда 1 и 3 символ можно пометить зеленым. Про 2-й символ пока ничего непонятно. Сдвинем палиндром на единицу вправо, получим, что 2 и 4 символы можно покрасить в один цвет. Так, сдвигаясь каждый раз на единицу, мы получим, что все символы на нечётных позициях зелёные, а на чётных — синие. Более строго можно доказать этот факт с помощью метода математической индукции, например.
Теперь, когда мы поняли, что надо искать, вернёмся непосредственно к задаче. Для краткости будем называть подстроки, которые являются нечётными палиндромами, хорошими. Надо изменить не более K символов так, чтобы максимизировать длину хорошей подстроки в последовательности.
Сперва разберёмся, как сделать из произвольной подстроки хорошую. Надо заменить на один и тот же символ все элементы на чётных позициях и отдельно заменить на нечётных.
Чтобы сделать как можно меньше замен, стоит выбрать в качестве единого символа самый частый среди тех, что стоят на чётных или нечётных позициях. Найти самый частый символ можно с помощью словаря (хеш-мапа, хеш-таблицы) отдельно для чётных и нечётных позиций. Алфавит в текущей задаче ограничен 26 символами, поэтому счётчик будет занимать константное количество дополнительной памяти.
Пройдёмся один раз по строке и добавим единицу в ячейку нужного словаря по текущему символу. Далее найдём в каждом словаре самый частый символ (если символов с максимальным числом вхождений несколько, то можно выбрать любой). Именно на этот символ надо заменить все элементы на чётных или нечётных позициях.
Теперь попробуем сделать как можно более длинную хорошую подстроку, которая начинается строго в символе с номером L. Указатель R будет отмечать ту позицию, до которой мы сумели расширить хорошую подстроку. Будем шагать указателем R вправо, начиная от позиции L. На каждом шаге будем учитывать в счётчике символов для чётных и нечётных позиций очередной символ. Прежде чем передвинуть R на шаг вправо, проверим по счётчикам, что сделать подстроку с L до R хорошей можно не более чем за K операций.
Если применить описанные действия независимо для всех L от 0 до n – 1, где n — длина исходной строки, а затем найти наиболее длинную найденную хорошую подстроку, то мы решим задачу. Однако временная сложность данного решения составит O(n^2), так как для каждой позиции L мы сделаем в худшем случае примерно n – L шагов при передвижении R.
Мы можем ускорить это решение с помощью техники двух указателей. Не будем обнулять счётчики и сбрасывать позицию R после того, как максимально отошли вправо от L. Переиспользуем текущую информацию при переходе от L к L+1. Для этого надо убрать из счётчиков элемент на позиции L — и всё. Затем можно продолжать делать проверки и отодвигать R вправо до тех пор, пока не исчерпаются K операций изменения элементов.
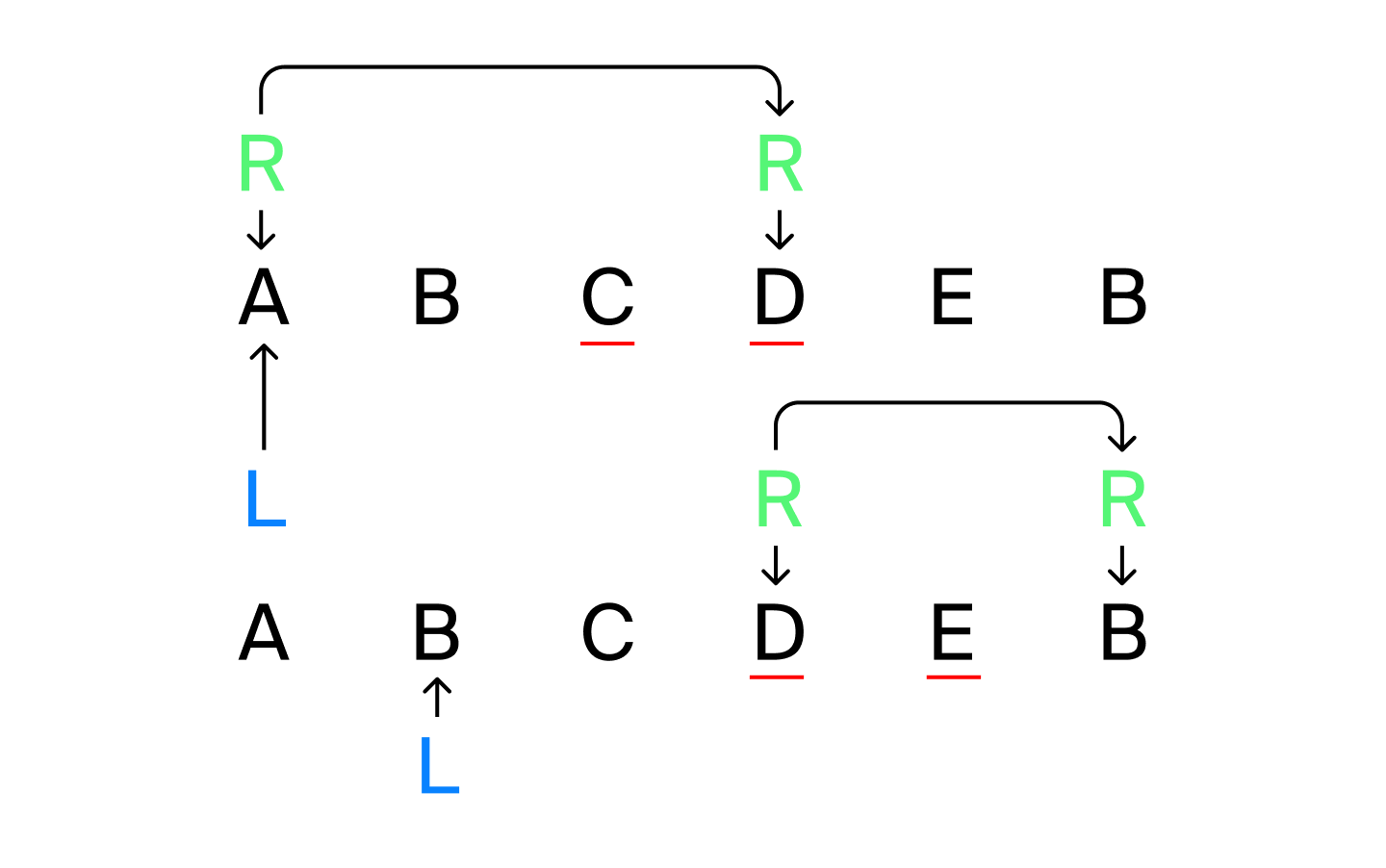
На рисунке выше показан ход указателей L и R, K=2. Подчёркнутые символы будут изменены при соответствующих L и R
Оценим сложность новой версии алгоритма. Указатель R суммарно сделает не более n шагов вправо, указатель L — тоже. Передвижение указателя сопровождается обновлением счётчиков и проверкой числа изменений для получения хорошей подстроки — эти действия выполняются за константное время, O(1). Таким образом мы получаем сложность O(n).
Мы выпутались из этой задачи, теперь можно запутываться в какую-нибудь другую.
Подробнее про метод двух указателей и про другие интересные приёмы мы рассказываем на курсе «Алгоритмы и структуры данных». Если вам интересна эта тема, приглашаю на наш курс.

Продолжение под катом.
Что такое палиндром
Палиндромом называется строка, которая одинаково читается как слева направо, так и справа налево. Например, слово «АТАТА» — это палиндром, а вот слово «АЙАЙАЙ» — нет.

Пример палиндрома из латинских слов: он составлен таким образом, что в каком бы направлении вы ни начали читать текст, получится одно и то же
Известный кинематографический палиндром — название вышедшего в 2020 году фильма «Довод» (англ. «Tenet»). Русская адаптация в каком-то плане уникальна, потому что у нас нашлась подходящая альтернатива слову «tenet», которая тоже является палиндромом. На многих других языках (в том числе славянских) название фильма оставили как есть. Например, на украинском это «ТЕНЕТ» (Википедия).

Постановка задачи
Итак, задача. Подготовьтесь морально.
Нечётным палиндромом будем называть такую строку, у которой все подстроки нечётной длины являются палиндромами. Суть задачи в том, чтобы в данной строке заменить не более K символов так, чтобы максимизировать длину самой длинной подстроки, которая является нечётным палиндромом.Всё, клубок запутался. Начнём распутывать.
Вот несколько примеров нечётных палиндромов: «ATATA», «KKKKKKKK», «ABA», «ZO».
Рассмотрим подробнее первую строку — АТАТА. Выпишем все её подстроки нечётной длины:
- A, T, A, T, A — однобуквенное слово всегда палиндром
- ATA, TAT, ATA — очевидно, палиндромы
- ATATA — тоже
В слове ZO нет подстрок нечётной длины больше чем в одну букву. И «Z», и «O» — палиндромы, поэтому «ZO» — нечётный палиндром.
Пусть нам дана строка ABCDEF, и мы можем заменить не более одного символа (K=1), чтобы сделать из неё нечётный палиндром. Оптимальным решением было бы, например, заменить первую букву на C, тогда мы получили бы CBCDEF, где длина наибольшей подстроки, являющейся нечётным палиндромом, была бы равна трём (это CBC).
С тем же успехом мы могли бы прийти к варианту ABCFEF.
А вот если изначально у нас была строка ZXXXZ, и опять можно изменить не более одного символа, то надо заменить средний, так как ZXX и XXZ не являются палиндромами. В итоге мы получим ZXZXZ.
Структура нечётного палиндрома
Теперь заметим кое-что в рассмотренных примерах. Все нечётные палиндромы имеют схожую структуру: в них чередуются буквы (или все буквы одинаковые). И это действительно единственная форма, которую имеет нечётный палиндром. Почему это так?
Посмотрим ещё раз на определение: нечётным палиндромом будем называть такую строку, у которой все подстроки нечётной длины являются палиндромами. Если все подстроки нечётной длины являются палиндромами, то и все подстроки длины 3 являются палиндромами. Отсюда сразу же следует, что на чётных позициях не может быть двух различных букв, то же самое верно для нечётных.

На рисунке выше показано, как получается чередующаяся структура строки. Одинаковым цветом выделены одинаковые символы. Сначала посмотрим на палиндром длины 3, который начинается в самом первом символе исходной строки. Тогда 1 и 3 символ можно пометить зеленым. Про 2-й символ пока ничего непонятно. Сдвинем палиндром на единицу вправо, получим, что 2 и 4 символы можно покрасить в один цвет. Так, сдвигаясь каждый раз на единицу, мы получим, что все символы на нечётных позициях зелёные, а на чётных — синие. Более строго можно доказать этот факт с помощью метода математической индукции, например.
Теперь, когда мы поняли, что надо искать, вернёмся непосредственно к задаче. Для краткости будем называть подстроки, которые являются нечётными палиндромами, хорошими. Надо изменить не более K символов так, чтобы максимизировать длину хорошей подстроки в последовательности.
Сперва разберёмся, как сделать из произвольной подстроки хорошую. Надо заменить на один и тот же символ все элементы на чётных позициях и отдельно заменить на нечётных.
Чтобы сделать как можно меньше замен, стоит выбрать в качестве единого символа самый частый среди тех, что стоят на чётных или нечётных позициях. Найти самый частый символ можно с помощью словаря (хеш-мапа, хеш-таблицы) отдельно для чётных и нечётных позиций. Алфавит в текущей задаче ограничен 26 символами, поэтому счётчик будет занимать константное количество дополнительной памяти.
Пройдёмся один раз по строке и добавим единицу в ячейку нужного словаря по текущему символу. Далее найдём в каждом словаре самый частый символ (если символов с максимальным числом вхождений несколько, то можно выбрать любой). Именно на этот символ надо заменить все элементы на чётных или нечётных позициях.
Наивное решение
Теперь попробуем сделать как можно более длинную хорошую подстроку, которая начинается строго в символе с номером L. Указатель R будет отмечать ту позицию, до которой мы сумели расширить хорошую подстроку. Будем шагать указателем R вправо, начиная от позиции L. На каждом шаге будем учитывать в счётчике символов для чётных и нечётных позиций очередной символ. Прежде чем передвинуть R на шаг вправо, проверим по счётчикам, что сделать подстроку с L до R хорошей можно не более чем за K операций.
Если применить описанные действия независимо для всех L от 0 до n – 1, где n — длина исходной строки, а затем найти наиболее длинную найденную хорошую подстроку, то мы решим задачу. Однако временная сложность данного решения составит O(n^2), так как для каждой позиции L мы сделаем в худшем случае примерно n – L шагов при передвижении R.
Улучшаем асимптотику решения
Мы можем ускорить это решение с помощью техники двух указателей. Не будем обнулять счётчики и сбрасывать позицию R после того, как максимально отошли вправо от L. Переиспользуем текущую информацию при переходе от L к L+1. Для этого надо убрать из счётчиков элемент на позиции L — и всё. Затем можно продолжать делать проверки и отодвигать R вправо до тех пор, пока не исчерпаются K операций изменения элементов.

На рисунке выше показан ход указателей L и R, K=2. Подчёркнутые символы будут изменены при соответствующих L и R
Оценим сложность новой версии алгоритма. Указатель R суммарно сделает не более n шагов вправо, указатель L — тоже. Передвижение указателя сопровождается обновлением счётчиков и проверкой числа изменений для получения хорошей подстроки — эти действия выполняются за константное время, O(1). Таким образом мы получаем сложность O(n).
Мы выпутались из этой задачи, теперь можно запутываться в какую-нибудь другую.
Подробнее про метод двух указателей и про другие интересные приёмы мы рассказываем на курсе «Алгоритмы и структуры данных». Если вам интересна эта тема, приглашаю на наш курс.


DareDen
А теперь задача со звездочкой: найти практическое применение (хотя бы два случая) данного, бесспорно, интереснейшего алгоритма :). Мне реально интересно, это не издевка.
Romanchenko28 Автор
Где нужны сами палиндромы — сложно сказать. Возможно, при анализе каких-то паттернов в последовательности ДНК может пригодиться (или это моя фантазия). А два указателя — достаточно популярная техника. Можно считать скользящее среднее в окне, да почти любые статистики в окне, если мы говорим об анализе временных рядов. Тут надо задачи конкретные смотреть, чтобы дальше разбираться. Например, можно вот это почитать algorithmica.org/tg/mergesort
DareDen
Палиндромы в ДНК такая же редкость, как и в лингвистике. Аминокислоты кодируются триплетом-кодоном, так что вероятность палиндромности длиннее трех даже пониже будет.
Техника указателей популярная, не спорю, но вот устал я от задач по алгоритмистике без практического применения… А в Яндексе, я смотрю, они все еще популярны в собеседованиях ;)
wataru
В биоинформатике не только ДНК, но и белки с аминокислотами. И вот там палиндромы могут быть запрасто.
DareDen
Таак, давайте разберемся. Аминокислоты — состоят из атомов, белки — из аминокислот, которые кодируются триплетами-кодонами. Насколько мне известно, «атомные» палиндромы очень редкие, особенно среди длинных — более трех атомов. Аминокислоты — ну какая там-то полиндромность? Там есть конец с азотом, который по определению, не может совпадать с другим, иначе это не аминокислота.
Ну и про палиндромность в ДНК — не надо понимать ТУ палиндромность, как палиндромность в статье и лингвистике. Ниже уже отписался об этом.
wataru
Белки — последовательности аминокислот. Последовательность может быть одинаковая туда и обратно.
DareDen
Если они будут одинаковы «туда и обратно» это нарушит главный принцип генетики — комплементарность ДНК, молекула просто разойдется по швам.
«For example, the DNA sequence ACCTAGGT is palindromic because its nucleotide-by-nucleotide complement is TGGATCCA» — вот что понимают под палиндромом генетики, мало того, что наоборот перевернутая, так еще и комплементарная. И, еще раз повторюсь, это не тот палиндром, что в статье.
wataru
Конкретно этот алгоритм с палиндромом вряд ли можно применить где-либо. Сами полиндромы в биоинформатике иногда применяются, всякие задачи с заменой минимального количества символов для получения нужной подстрки — тоже. Но все вместе — вряд ли.
Метод двух указателей же — вообще весьма полезная штука. Возникает много где. Начиная от геометрических задач, вроде поиска расстояния между двумя выпуклыми фигурами (игровые движки), и заканчивая всякой обработкой логов и статистикой. Например, вам надо узнать максимальную нагрузку сервера в запросах/с и у вас есть лог с временами запросов.
airy
https://link.springer.com/article/10.1023/A:1023454111924
DareDen
The meaning of palindrome in the context of genetics is slightly different from the definition used for words and sentences. Вики Это не те палиндромы, которые описаны тут :)
wataru
Из статьи
В протеинах палиндромы обычные, строковые.
Dolios
Вы игре на музыкальных инструментах обучались? Практическое применение гаммам можете назвать?
DareDen
Запросто: правильная постановка пальцев, правильное перемещение пальцев, развитие нужных мускулов, запоминание нот. У гамм — огромная польза от повторений. Алгоритм, подобный описанному в статье, забавный курьез на один раз прочитать.
Dolios
Решение подобных задач дает следующее практическое применение: тренирует умение анализировать проблему, искать пути решения, анализировать сложность, анализировать расход памяти, развивает нужные нейронных связи. У решения таких задач — огромная польза от повторений. Конкретная гамма до мажор, забавный курьез на один раз сыграть.
Подход "2 указателя" используется во многих алгоритмах, в том числе, имеющих практическое применение, о чем вам уже написал wataru.
DareDen
У решения ТАКОЙ задачи или ТАКИХ? :) От даже одной гаммы тоже польза, от постоянного решения одной задачи ее нет (таки да, я тоже умею в крючкотворство :)).
Dolios
От даже одной задачи тоже польза. Примерно как от одной гаммы. Поэтому и задачи решают разные и гаммы разные играют, чтобы польза больше была.
Romanchenko28 Автор
интересная параллель с гаммами. Примерно то же самое, наверное, с геометрией, которая не вычислительная, а которой больше в школе и на математических кружках развлекаются. Сейчас уже практической пользы сравнительно мало, но вот сам процесс решения очень может завлечь (ну у меня по крайней мере так было, за всех не говорю).
StjarnornasFred
Такс, а можно поподробнее про геометрию? Это, на минуточку, одна из важнейших областей математики. Понятно, что польза школьных задач её выходит за стены школы, но ведь при инженировании зданий, механизмов и прочего подобного чертёжная геометрия ("начерталка") очень важна.
Romanchenko28 Автор
я не говорю про начертательную геометрию и все другие практически применимые виды геометрии, скажем так. Графика та же, рендереры. Я, скорее, про список n примечательных фактов и приёмов, которые могут пригодиться «когда-нибудь в какой-нибудь задаче». Вот это вообще моя любимое — энциклопедия замечательных точек треугольника faculty.evansville.edu/ck6/encyclopedia/ETC.html