Израильские учёные из Института физики им. Рака при Еврейском университете предложили новый способ упрощения задачи трёх тел, позволяющий точно оценить вероятность покидания системы любым из этих тел. Работа опубликована в журнале Celestial Mechanics and Dynamical Astronomy.

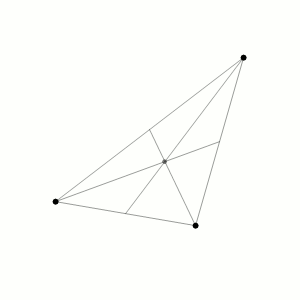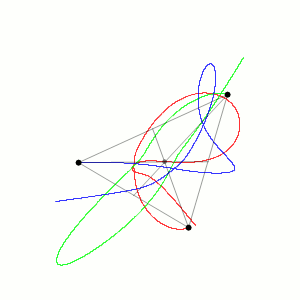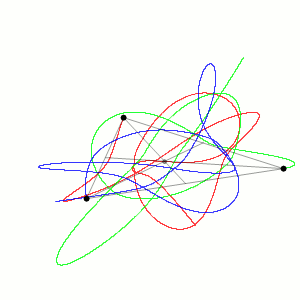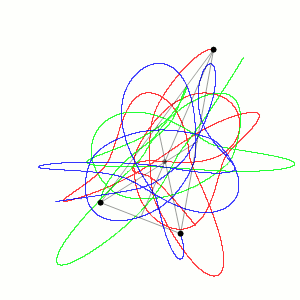
Задача трёх тел подразумевает описание поведения небесных тел в трёхмерном пространстве, взаимно притягивающихся друг к другу. Ею впервые заинтересовался Исаак Ньютон, пытавшийся в XVII веке описать движения планет Солнечной системы. Он попробовал вывести формулу, описывающую движение Луны вокруг Земли с учётом того, что Земля движется вокруг Солнца. Однако оказалось, что это одна из тех задач, которую легко сформулировать и трудно решить.

Проблемой в разное время занимались такие величайшие математики, как Эйлер, Лагранж, Якоби и Пуанкаре. Анри Пуанкаре в XIX веке обнаружил, что поведение системы отличается крайней чувствительностью к начальным условиям – первоначальным положениям и скоростям тел. Таким образом, система является хаотичной и не имеет детерминистских решений.

Появление вычислительных мощностей в XX веке позволило подступиться к этой задаче при помощи численного моделирования. Оказалось, что при неких достаточно общих допущениях в системе трёх тел хаотичные периоды движения сменяются периодическими, пока, наконец, она не распадается на пару тел, вращающихся относительно центра их масс, и третье тело, удаляющееся от них.

Из-за хаотичного поведения системы нельзя было рассчитывать на то, что компьютеры выдадут точные и долгосрочные прогнозы поведения такой системы. Однако в 1976 году появилась идея о возможности статистического решения этой задачи, предсказывающего вероятность убегания одного из тел.

Даже такая задача оказалась настолько сложной, что её удалось решить только 45 лет спустя. Доктор Николас Стоун из Еврейского университета со своими коллегами использовали новый метод расчётов, и впервые получили замкнутое математическое выражение для статистического решения задачи.

Предыдущие методы опирались на т.н. фазовое пространство – набор всех положений и скоростей частиц, составляющих систему. К примеру, фазовое пространство единственной частицы, которая может двигаться по отрезку длиной метр со скоростями не более двух метров в секунду, будет представлять собой прямоугольник с шириной в 1 м и длиной в 4 м/с – поскольку скорость может иметь как положительный, так и отрицательный знак.

Обычно физики имеют дело с объёмом фазового пространства, или, сокращённо, с фазовым объёмом. Например, вероятность найти частицу в левой половине отрезка связывается с объёмом левой половины прямоугольника в фазовом пространстве, составляющим половину объёма всего прямоугольника.

Поскольку три тела не ограничены в пространстве, а сила гравитации действует на любом расстоянии, объём фазового пространства в этой задаче бесконечен, и, следовательно, вероятности тоже бесконечны. Поэтому все предыдущие методы принимали некий объём пространства за «область сильного взаимодействия», игнорируя всё остальное.

В новой работе предлагается изучать «поток фазового объёма». Если мы представим себе ёмкость с газом, в стенке которой есть пара отверстий, то вероятность того, что конкретная молекула вылетит через одно из них, будет пропорциональной потоку газа через каждое из отверстий.

Поток конечен даже в бесконечном пространстве, поэтому новый подход одновременно избегает бесконечных вероятностей и не прибегает к искусственному ограничению объёма. В итоге теория позволяет предсказать вероятность убегания любого из тел. По словам профессора Кола, одного из авторов работы, миллионы компьютерных симуляций показывают, что предсказания теории очень хорошо соответствуют численным компьютерным симуляциям.

Ожидается, что исследование повлияет как на решение различных задач астрофизики, так и на понимание целого класса проблем механики.