В этой статье описан псевдоспектральный метод численного решения уравнений матфизики, используемый в вычислительной гидродинамике, геофизике, климатологии и во многих других областях.

Для начала рассмотрим простую одномерную задачу распространения тепла в стержне. Уравнение, описывающее распространение тепла при некотором начальном распределении температуры по стержню:
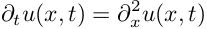
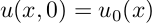
Такое уравнение решается аналитически методом разделения переменных, например здесь, но нас интересует как это можно сделать численно. Прежде всего нужно определиться, как считать вторую пространственную производную по х. Проще всего это делается каким-нибудь разностным методом, например:

Но мы поступим иначе. Распределение температуры есть функция координаты и времени, и в каждый момент времени эта функция может быть представлена в виде суммы ряда Фурье, который в численном виде обрезается на n-ом члене:

Где u^«с крышечкой» — это коэффициенты разложения ряда Фурье. Подставим выражение для ряда в уравнение переноса тепла:
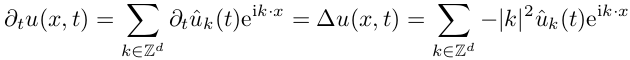
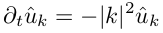
Получаем уравнение для коэффициентов Фурье, в котором отсутствует производная по координате! Теперь это обыкновенное дифференциальное уравнение, а не в частных производных, которое можно решить простым разностным методом. Уже легче, теперь остается найти коэффициенты разложения и в этом нам очень поможет быстрое преобразование Фурье (дальше FFT).
Логика здесь следующая:
1) в начальный момент времени дана функция координаты, описывающая распределение температуры по стержню;
2) разбиваем стержень на сетку из n точек;
3) находим комплексные коэффициенты Фурье с помощью алгоритма FFT, обозначим операцию как F(u);
4) умножаем полученные коэффиценты на -|k|2, получаем Фурье-образ второй производной. Аналогично можно получить Фурье-образ производной более высоких порядков p, достаточно умножить на (ik)p;
5) делаем обратное преобразование Фурье F-1(u), с помощью алгоритма IFFT, получаем значения второй производной в точках на сетке;
6) делаем шаг по времени, уже обычной разностной, явной или неявной, схемой;
7) повторяем.
Рассмотрим теперь как это работает в программе для Matlab/Octave. В качестве начального распределения температуры возьмем гладкую функцию u0=2+sin(x)+sin(2x), стержень длинной 2? разобьем на 50 точек, с шагом по времени h=0.1, граничные условия периодичные (кольцо).
Стоит отметить особенность алгоритма FFT в Matlab, связанную с тем, что полученные коэффициенты разложения на выходе d=fft(u) идут не по порядку, а смещены, первая половина на месте второй и наоборот. Cначала идут коэффициенты с номерами от 0 до n/2-1, потом с номерами от -n/2 до -1. С этим были проблемы…
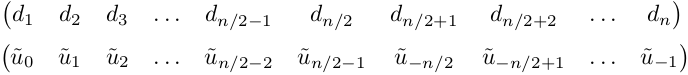
Полученное решение можно видеть на графике в виде «водопада» линий распределения температуры по х для каждого момента времени t. Видно, что решение испытываетсильные осциляции численную неустойчивость, связано это с невыполнением критерия Куранта. Избавиться от неустойчивости можно уменьшив шаг по времени, либо применяя более продвинутую неявную схему, например Кранка-Николсона.

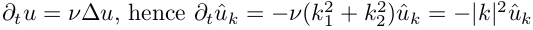
Начальные условия: u0 = 1 + sin(2X) + cos(2Y), где u теперь 2d-массив u(i,j). Используем неявную схему интегрирования по времени (т.е. выразим m+1 шаг через m-й):
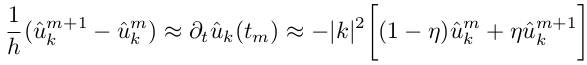
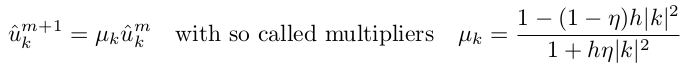
Можно доказать, что такая неявная схема никогда не расходится при ?>0.5, будем использовать ?=1. Таким образом каждое новое значение um+1 получаем умножением um на коэффициент ?k, зависящий от временного шага и волновых чисел k, т.е. ?k — это константа, которую не нужно пересчитывать на каждом шаге!


В волновом уравнении присутствует вторая производная по времени, поэтому задача сводится к системе двух обыкновенных диффуров, одна переменная — u, вторая — ut, схему по времени в коде использовал самую простую явную, поэтому точность небольшая, шаг по времени очень маленький, зато код выглядит относительно просто. Впрочем, этого хватает для демонстрации работоспособности метода.
Периодичные граничные условия:
Фиксированные граничные условия (0 на краях, отражение волн от границ):
В статье продемонстрировано несколько примеров применения спектрального метода для простых задач матфизики. Основная суть суть спектрального метода, это замена исходных диффренциальных уравнений в частных произодных на обыкновенные диффуры для коэффициентов разложения искомых функций по некоторому базису. Базисом могут быть синусы-косинусы, комплексные экспоненты, ортогональные полиномы, если требует геометрия — цилиндрические или сферические функции. Найденные коэффициенты в каждый момент времени позволяют восстановить искомое решение, а алгоритм FFT позволяет делать это быстро.
Преимуществами метода являются:
Недостатки тоже имеются:
Надеюсь, моя первая статья будет кому-нибудь полезна, как минимум это возможный старт для изучающих этот раздел численных методов. Жду критических замечаний к коду, оформлению и советов!

Одномерная задача распространения тепла по стержню
Для начала рассмотрим простую одномерную задачу распространения тепла в стержне. Уравнение, описывающее распространение тепла при некотором начальном распределении температуры по стержню:
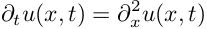
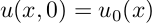
Такое уравнение решается аналитически методом разделения переменных, например здесь, но нас интересует как это можно сделать численно. Прежде всего нужно определиться, как считать вторую пространственную производную по х. Проще всего это делается каким-нибудь разностным методом, например:

Но мы поступим иначе. Распределение температуры есть функция координаты и времени, и в каждый момент времени эта функция может быть представлена в виде суммы ряда Фурье, который в численном виде обрезается на n-ом члене:

Где u^«с крышечкой» — это коэффициенты разложения ряда Фурье. Подставим выражение для ряда в уравнение переноса тепла:
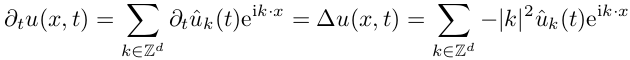
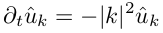
Получаем уравнение для коэффициентов Фурье, в котором отсутствует производная по координате! Теперь это обыкновенное дифференциальное уравнение, а не в частных производных, которое можно решить простым разностным методом. Уже легче, теперь остается найти коэффициенты разложения и в этом нам очень поможет быстрое преобразование Фурье (дальше FFT).
Логика здесь следующая:
1) в начальный момент времени дана функция координаты, описывающая распределение температуры по стержню;
2) разбиваем стержень на сетку из n точек;
3) находим комплексные коэффициенты Фурье с помощью алгоритма FFT, обозначим операцию как F(u);
4) умножаем полученные коэффиценты на -|k|2, получаем Фурье-образ второй производной. Аналогично можно получить Фурье-образ производной более высоких порядков p, достаточно умножить на (ik)p;
5) делаем обратное преобразование Фурье F-1(u), с помощью алгоритма IFFT, получаем значения второй производной в точках на сетке;
6) делаем шаг по времени, уже обычной разностной, явной или неявной, схемой;
7) повторяем.
Рассмотрим теперь как это работает в программе для Matlab/Octave. В качестве начального распределения температуры возьмем гладкую функцию u0=2+sin(x)+sin(2x), стержень длинной 2? разобьем на 50 точек, с шагом по времени h=0.1, граничные условия периодичные (кольцо).
Код для одномерного уравнения переноса тепла
clear all;
n = 50; % number of points
dx = 2*pi/n; % space step
x = 0:dx:2*pi-dx; % grid
h = 0.1; % temporal step
times = 10; % number of iterations in time
k = fftshift(-n/2:1:n/2-1); % wave numbers
k2 = k.*k;
u0 = 2 + sin(x) + sin(2*x); % initial conditions
u = zeros(times,n); % stores results
u(1,:) = u0;
uf = fft(u0); % Fourier coefficients of initial function
for i=2:times
uf = uf.*(1-h*k2); % next time step in Fourier space
u(i,:) = real(ifft(uf)); % IFFT to physical space
end
[X,T] = meshgrid(x,0:h:times*h-h);
waterfall(X,T,u)
Стоит отметить особенность алгоритма FFT в Matlab, связанную с тем, что полученные коэффициенты разложения на выходе d=fft(u) идут не по порядку, а смещены, первая половина на месте второй и наоборот. Cначала идут коэффициенты с номерами от 0 до n/2-1, потом с номерами от -n/2 до -1. С этим были проблемы…
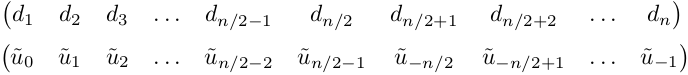
Полученное решение можно видеть на графике в виде «водопада» линий распределения температуры по х для каждого момента времени t. Видно, что решение испытывает

Двумерное уравнение диффузии
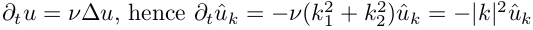
Начальные условия: u0 = 1 + sin(2X) + cos(2Y), где u теперь 2d-массив u(i,j). Используем неявную схему интегрирования по времени (т.е. выразим m+1 шаг через m-й):
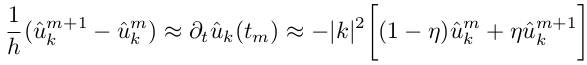
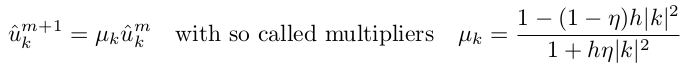
Можно доказать, что такая неявная схема никогда не расходится при ?>0.5, будем использовать ?=1. Таким образом каждое новое значение um+1 получаем умножением um на коэффициент ?k, зависящий от временного шага и волновых чисел k, т.е. ?k — это константа, которую не нужно пересчитывать на каждом шаге!
Код для двумерного уравнения диффузии
clear all;
eta = 1;
n = 32; % number of points
dx = 2*pi/n; % space step
x = 0:dx:2*pi-dx;
y = x;
[X, Y] = meshgrid(x,y);
h = 0.01; % temporal step
times = 30; % number of iterations in time
k1 = meshgrid(fftshift(-n/2:1:n/2-1),ones(n,1));
k2 = k1';
ks = k1.*k1 + k2.*k2;
mu = (1-(1-eta)*ks^2*h)./(1+eta*ks.^2*h); % stores multipliers
u0 = 1 + sin(2*X) + sin(2*Y); % initial temperature
u = zeros(times,n,n); % stores results
umin=min(min(u0));
umax=max(max(u0));
u(1,:,:) = u0;
uf = fft2(u0);
for i=2:times
uf = mu.*uf; % time step
u(i,:,:) = real(ifft2(uf));
end
createGif('diffusion2d.gif',X,Y,u,times,1,[0 2*pi 0 2*pi umin umax]);
Сохранение гифки
function createGif(name,X,Y,u,times,every,ax)
% creates gif movie form 3D array
% save results to gif file
gifka = name;
clf;
pic = surf(X,Y,squeeze(u(1,:,:))),axis(ax);
for i=1:every:times
set(pic,'zdata',squeeze(u(i,:,:))), drawnow;
M(i) = getframe;
frame = getframe;
im = frame2im(frame);
[imind,cm] = rgb2ind(im,256);
if i == 1;
imwrite(imind,cm,gifka,'gif','Loopcount',inf);
else
imwrite(imind,cm,gifka,'gif','WriteMode','append','DelayTime',.1);
end
end
end

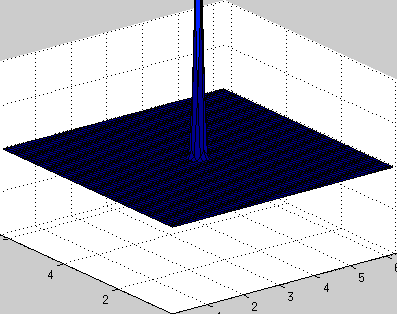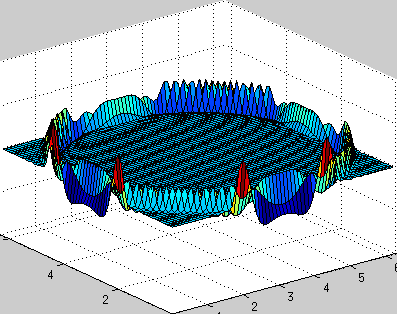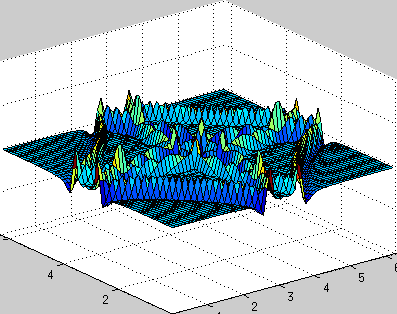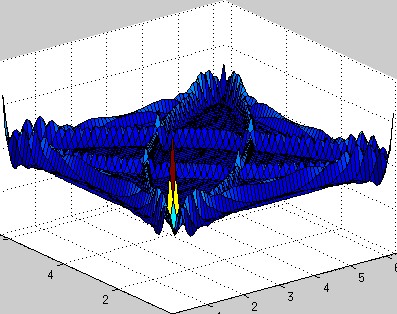
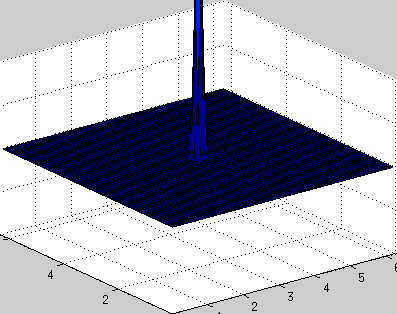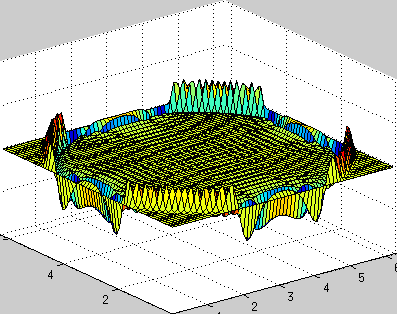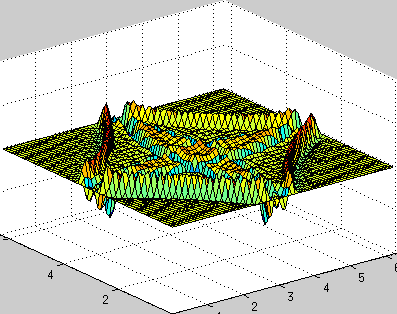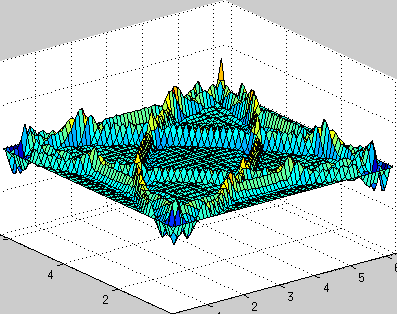
Двумерное волновое уравнение

В волновом уравнении присутствует вторая производная по времени, поэтому задача сводится к системе двух обыкновенных диффуров, одна переменная — u, вторая — ut, схему по времени в коде использовал самую простую явную, поэтому точность небольшая, шаг по времени очень маленький, зато код выглядит относительно просто. Впрочем, этого хватает для демонстрации работоспособности метода.
Код для двумерного волнового уравнения
clear all;
a = 1; % speed of wave propagation
n = 64; % number of points
dx = 2*pi/n; % space step
x = 0:dx:2*pi-dx;
y = x;
[X, Y] = meshgrid(x,y);
h = 0.01; % temporal step
times = 1000; % number of iterations in time
% explanation of this part is here www.staff.uni-oldenburg.de/hannes.uecker/pre/030-mcs-hu.pdf
k1 = meshgrid(fftshift(-n/2:1:n/2-1),ones(n,1));
k2 = k1';
ks = k1.*k1 + k2.*k2;
u0 = exp(-100*((X-pi).^2 + (Y-pi).^2)); % profile of initial velocity u
ut0 = zeros(n,n); % profile of initial acceleration ut
u = zeros(times,n,n); % stores velocity profile for every time steps
u(1,:,:) = u0;
uf = fft2(u0);
uft = fft2(ut0);
for i=2:times
uft_new = uft - a*h*ks.*uf;
uf = uf + 0.5*h*(uft+uft_new);
uft = uft_new;
% == fixed boundary conditions
% u0 = real(ifft2(uf));
% u0(1,:) = 0; u0(end,:) = 0;
% u0(:,1) = 0; u0(:,end) = 0;
% uf = fft2(u0);
% == fixed boundary conditions
u(i,:,:) = real(ifft2(uf));
end
createGif('wave2d_periodic_bc.gif',X,Y,u,times,10,[0 2*pi 0 2*pi -.2 .2]);
Периодичные граничные условия:

Фиксированные граничные условия (0 на краях, отражение волн от границ):

Выводы
В статье продемонстрировано несколько примеров применения спектрального метода для простых задач матфизики. Основная суть суть спектрального метода, это замена исходных диффренциальных уравнений в частных произодных на обыкновенные диффуры для коэффициентов разложения искомых функций по некоторому базису. Базисом могут быть синусы-косинусы, комплексные экспоненты, ортогональные полиномы, если требует геометрия — цилиндрические или сферические функции. Найденные коэффициенты в каждый момент времени позволяют восстановить искомое решение, а алгоритм FFT позволяет делать это быстро.
Преимуществами метода являются:
- Хорошая точность для «хороших» функций. С увеличением количества точек сетки n ошибка метода конечных разностей падает как O(N-m)) (где m — некая постоянная, которая зависит от порядка метода и гладкости функции), а для спектрального метода точность может быть экспоненциальной O(cN), где 0 < c < 1.
- Относительная простота использования, особенно при нахождении производных высоких степеней, для сравнения метод конечных разностей предполагает использование довольно сложных формул. Применение эффективного алгоритма FFT дает сложность O(N log(N)), что приемлемо для достаточно больших задач
- Спектральный метод эффективен в отношении памяти, поэтому широко используется в геофизике, моделировании климата и метеорологии.
Недостатки тоже имеются:
- Феномен Гиббса, очень нехорошее явление, сильно влияющее на точность на краях области
- Более требователен к вычислительным ресурсам на степень свободы, чем в разностных методах
- Плохо применим к задачам с нестандартной геометрией, и граничным условиям, отличным от периодических.
Надеюсь, моя первая статья будет кому-нибудь полезна, как минимум это возможный старт для изучающих этот раздел численных методов. Жду критических замечаний к коду, оформлению и советов!
Использованые источники
- Отличный обзор от Hannes Uecker с примерами кода, часть из которых я использовал в этой статье
- Небольшая, и поэтому замечательная книга Lloyd N. Trefethen, Spectral Methods in MATLAB
- Фундаментальная книга John P.Boyd «Chebyshev and Fourier Spectral Methods»
Комментарии (5)

FransuaMaryDelone
22.09.2015 17:27Жду критических замечаний
«Вы хотите критических замечаний?! Их есть у меня!» (с)
А вообще, радостно читать, что всё хорошо, что есть метод, что жизнь прекрасна. Жаль только, что всё легкое уже порешали на БЭСМ.


Uranix
В одномерной теплопроводности у вас не осцилляции, а обычная неустойчивость от большого шага по времени. Проверьте условие Куранта, скорее всего, оно у вас нарушено. Осцилляциями обычно называют немонотонность численного решения при сохранении устойчивости.
DanmerZ
Ок, с вами согласен, использовал некорректный термин. Можно поставить меньше временной шаг и условие Куранта выполнится, схема не будет расходится.