
Хабр, привет!
Мы продолжаем цикл статей ([1], [2], [3]), посвященных применению ML-методов в ряде задач управления кредитным риском. В этой мы расскажем про задачу, которая возникает в ходе жизненного цикла кредитного договора: моделирование доли невозврата по договору в случае его дефолта (loss given default, LGD).
Зачем это нужно делать, ведь дефолт случился и на первый взгляд кажется, что прогнозировать уже ничего не нужно? Действительно, можно считать, что клиент уже ничего не вернет и под такие договоры закладывать 100%-ное резервирование.
Однако в действительности после дефолта клиенты могут вносить платежи или, если договор был обеспечен (залог), то в ходе продажи обеспечения вся сумма договора или ее часть могут быть погашены за счет суммы реализации (продажи) залога.
Также стоит обратить внимание, что для банковской сферы (в других индустриях зависит от продукта и политики резервирования) прогноз должен производиться как по договорам, находящимся в дефолте (default сегмент), так и по тем, по которым нет дефолта на момент расчета резервов (non-default сегмент). Разработка прогнозной модели возможна только на договорах в дефолте. В этом случае возникает проблема переноса модели на сегмент недефолтных договоров.
Об особенности расчета компоненты LGD, ее моделирования, распространении прогноза на весь портфель, а также подходах к валидации расскажем далее.
Стоит отметить, что доля невозврата существенно зависит от типа продукта (например, ипотека vs. кредитная карта), сегмента клиентов (ЮЛ vs. ФЛ), индустрии (банк vs. телеком) или даже от типа банка. При этом исследуемая величина может варьироваться в широком диапазоне (цифры отражают порядок различия): от 10–20% для обеспеченных кредитов (ипотека, ЮЛ с обеспечением) до 80–90% (для кредитных карт ФЛ).
В связи с таким разбросом возникает потребность прогнозирования этой величины — если предполагать, что невозврат будет 100%, то мы, с большой вероятностью, перезакладываемся и должны нести бремя дополнительных расходов, тогда как в случае качественного прогноза можно “распустить” часть резервов и получить дополнительную прибыль за счет их использования в бизнесе.
Теоретический подход к прогнозированию LGD мы проиллюстрируем примером из нашей практики.
Особенности разбираемого случая:
- в исходных данных по договорам содержалась только информация об истории балансов и просрочек, а также факты продажи и списания договоров;
- мало информации о клиентах;
- глубина истории — около 2 лет.
Постановка задачи
Алгоритм сбора LGD
Сначала остановимся на том, как определяется моделируемая величина. Для каждого договора собирается история платежей после дефолта (рис. 1). Такие платежи называют восстановлением. Временной горизонт может варьироваться от года до трех–пяти лет, что зависит от типа заемщиков (ЮЛ, физ.лица), глубины данных и особенности бизнес-процессов в банке. Восстановление дисконтируют, если анализируется длительный период, известно точное время внесения денег заемщиком (до месяца, а не агрегированные данные за год), а также есть значительная инфляция (подробнее см. [2]).
Ниже приведена иллюстрация алгоритма сбора LGD.
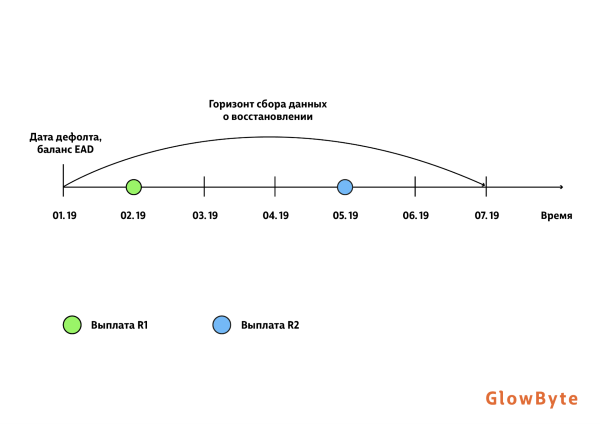
LGD рассчитывается формуле:


Целевая переменная модели
Поскольку мы прогнозируем возврат денежных средств для клиентов, которые уже находятся в дефолте, в качестве целевой переменной целесообразнее использовать баланс не на момент дефолта, как описано выше, а текущий (момент наблюдения и/или скоринга), который учитывает возможное внесение денег на счет после дефолта. Поэтому величина LGD модифицируется и «баланс на момент дефолта» заменяется на «баланс клиента на дату наблюдения», полученный показатель используется как целевая переменная:

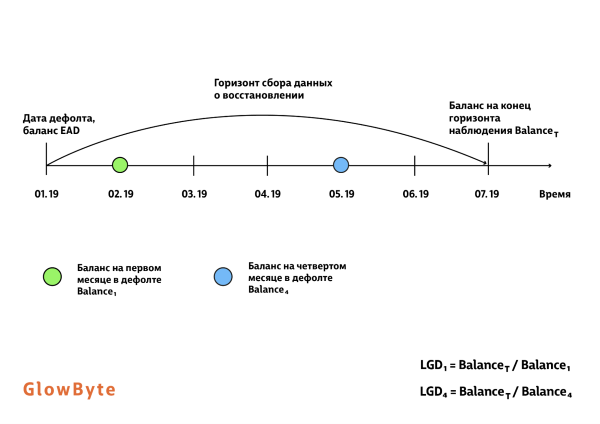
Рисунок 2. Алгоритм сбора целевого события
Благодаря такому подходу мы получаем модель, которая гибко реагирует на изменение баланса находящегося в дефолте клиента, что дает более точную оценку уровня потерь. Хотя LGD теперь определяется в момент времени , горизонт для сбора данных о восстановлении остается фиксированным и отсчитывается от даты дефолта.
Учет бизнес-процессов
При расчете LGD должны быть учтены события, которые могут происходить с кредитным договором после дефолта.
- Продажа:

- Списание:

- Реструктуризация:

- Выздоровление, погашение долга и выход из дефолта:

Для более детального ознакомления с дополнительными методами оценки LGD (в том числе workout и market LGD) следует обратиться, например, к обзору [4].
Сегмент для моделирования
Расчет LGD возможен только после наступления дефолта. Поэтому моделирование LGD производится исключительно на договорах в состоянии дефолта. Дальнейшее практическое использование модели LGD предполагает ее применение ко всем договорам (как не, так и находящимся в дефолте), поскольку для каждого договора должна быть получена оценка ожидаемых потерь (EL). Подробнее об EL можно прочитать в [1].
Читатели, имеющие практический опыт в машинном обучении, наверняка понимают, что для модели, которая обучается на одном сегменте наблюдений, а применяется на другом, нужны особая схема и метод валидации. Рекомендации по валидации модели LGD будут даны далее.
Теперь, когда целевая переменная модели определена, можно переходить к формированию выборки и сбору атрибутов.
Выборка для моделирования
Основные драйверы
Как уже было отмечено выше, LGD — это величина, сильно зависящая от бизнес-процессов. Для таких величин часто можно выделить несколько переменных, которые хорошо предсказывают их значения. Или в терминах машинного обучения: для LGD существует несколько предикторов, которые вне зависимости от конкретной задачи дают наибольший вклад в модель. Такие величины еще называют основными драйверами.
Для LGD можно выделить следующие основные драйверы:
- количество дней в просрочке (далее dpd);
- возраст дефолта (далее default age) — период времени от даты дефолта по договору до текущей даты наблюдения.
Default age и dpd важные статистики, которые показывают динамику LGD и по которым можно валидировать расчеты. Если dpd и default age увеличиваются, то доля невозврата монотонно возрастает (см. графики ниже). Здесь стоит отметить разницу между драйверами, поскольку на первый взгляд кажется, что это одно и то же.
Напомним [2], что часто dpd рассчитывается по методу FIFO: при наличии платежей со стороны заемщика величина просрочки не будет увеличиваться, а возраст дефолта, если задолженность не погашена полностью, будет увеличиваться. Такой подход, в частности, позволяет более осознанно обрабатывать случаи, когда заемщик фиксируется на долгое время в каком-то из бакетов просрочки.
Алгоритм построения распределений
Распределение LGD по dpd
Распределение LGD по default age
- Для каждого наблюдения рассчитываем LGD, текущий баланс и потери по договору.
- Усредняем рассчитанные значения внутри групп по dpd. За единицу измерения удобнее брать месяц, поскольку история по договорам обычно обновляется ежемесячно.
Распределение LGD по default age
- Для каждого наблюдения рассчитываем текущий баланс и потери по договору.
- Далее суммируем рассчитанные значения внутри групп по default age (шаг дискретизации — 1 месяц).
- По суммарным значениям текущего баланса и потерь по договорам рассчитываем кумулятивные суммы в порядке увеличения default age.
- Итоговое распределение LGD по default age рассчитывается как отношение кумулятивных потерь по договорам к текущему балансу по ним.
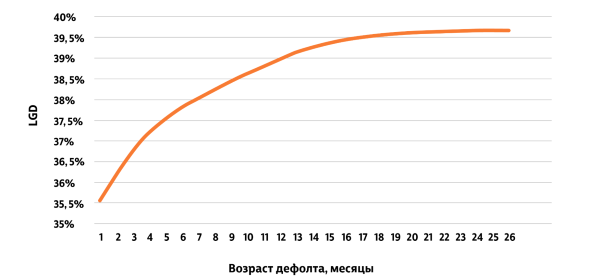
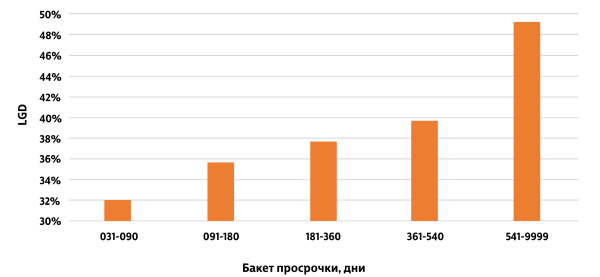
Предикторы
Помимо основных драйверов нам были доступны следующие блоки атрибутов:
- наличие других кредитных договоров у клиента и его платежи по ним;
- динамика просрочки платежей по «дефолтному» договору;
- утилизация лимита по договору.
Описанные блоки атрибутов позволяют построить довольно точную и гибкую модель LGD.
Моделирование
Для моделирования LGD используются разные методы [4] машинного обучения, в том числе продвинутые (например, ансамбли деревьев или нейронные сети). Среди стандартных методов расчета LGD стоит упомянуть цепочно-лестничный метод и метод Борнхуэттера–Фергюсона. Если говорить про регрессионные методы, то, учитывая форму распределения LGD (часто U-образная, с модами около 0 и 1), в общем случае следует использовать GLM — обобщенную модель линейной регрессии — с некоторой функцией связи (link function), которая учитывает распределение целевой переменной, отличное от нормального [5].
В данной части мы остановимся на методах, которые использовались в рамках описываемого проекта, а с описанием методологии моделирования LGD предлагаем ознакомиться в [1].
Выбор модели
Выбор метода машинного обучения производится с учетом:
- распределения LGD по dpd и default age;
- распределения LGD;
- формата, в котором необходимо предоставить результат моделирования;
- баланса портфеля по договорам.
Следует отметить, что может быть необходимо несколько моделей для разных сегментов клиентов. Именно так мы и поступили для решения нашего кейса.
Логистическая регрессия
Логистическая регрессия — один из самых распространенных и известных методов машинного обучения. Из его преимуществ можно выделить скорость работы, простоту настройки и интерпретации, большое количество готовых реализаций.
Логистическую регрессию стоит использовать, если:
- распределение LGD по dpd и default age монотонно-возрастающее;
- результаты модели нужно представить в виде скоркарты;
- баланс распределен по договорам практически равномерно (отсутствуют аномально большие по балансу договоры или их число незначительно).
Для логистической регрессии необходим бинарный таргет (0 или 1), но LGD величина непрерывная. Поэтому моделируемую величину бинаризуют одним из способов:
- взвешенным методом;
- отсечением по фиксированному пороговому значению;
- отсечением по случайному пороговому значению.
Подробнее о методах бинаризации можно прочитать в ([3]) или ([6]).
Бинаризованный LGD можно моделировать с помощью логистической регрессии. Смоделированная вероятность класса 1 трактуется как прогнозное значение LGD.
Взвешенная регрессия
Взвешенная регрессия относится к стандартным методам машинного обучения. Отличие от обычной регрессии: веса наблюдения используются в функционале ошибки.
Данный метод применяется, когда
- распределение LGD по dpd и default age монотонно-возрастающее;
- скоркарта не требуется;
- значительная доля баланса портфеля сосредоточена в небольшом количестве договоров.
В последнем случае использование баланса на дату перед дефолтом в качестве веса наблюдения может значительно повысить качество модели LGD.
Дерево решений
Дерево решений — отличная альтернатива регрессии, которая обычно точнее, но также проста в интерпретации и настройке.
Дерево решений стоит использовать, если:
- скоркарта не требуется;
- распределение LGD по dpd и/или default age не монотонно.
Распределение не монотонно, если с некоторого момента начинается списание большого числа имеющих высокий LGD ссуд. Поскольку LGD рассчитывается как усредненный показатель, эти ссуды увеличивают показатель LGD до момента списания и приводят к его снижению после.
Для корректного предсказания немонотонного поведения LGD в модель нужно одновременно включить два сильно коррелирующих фактора — dpd и default age, тогда методы на основе деревьев решений дают более высокое качество.
Применение модели
Напомним, что обучение модели LGD производится на сегменте дефолтных договоров (I), а применяется она ко всем, в том числе и недефолтным договорам. Поэтому важно при разработке модели учесть, как она будет изменена применительно к недефолтному сегменту (II). В идеальном случае разрабатывается отдельная модель на клиентах, которые не находятся в дефолте, но на горизонте расчета EL (часто 1 год) уйдут в дефолт.
Оговоримся, что для применения к дефолтному сегменту модель остается без изменений.
Рассмотрим пример стратегии корректировки модели для применения ее к недефолтному сегменту. Для недефолтного сегмента все предикторы, которые связаны с наступлением дефолта, принимаются равными среднему значению на дефолтном сегменте за первый месяц (default age = 1):

Валидация модели
По аналогии с применением модели валидация на дефолтном сегменте отличается от валидации на недефолтном сегменте. Цель валидации модели на дефолтном сегменте — оценка качества и стабильности модели. Валидация на недефолтном сегменте проверяет адекватность модели именно на этом сегменте.
Валидация на дефолтном сегменте
Качество модели определяется по ее общей предсказательной способности, а также предсказательной способности и стабильности на уровне входящих в нее факторов.
Для определения предсказательной способности модели используется модифицированный коэффициент Джини. А стабильность модели оценивается путем вычисления относительного изменения модифицированного коэффициента Джини между обучающей и тестовой выборками.
Предсказательная сила атрибутов обычно определяется коэффициентом Джини, а стабильность — относительным изменением коэффициента Джини и population stability index (PSI).
Для определения корректности предсказанных значений LGD используется значение коэффициента loss-shortfall. Данный коэффициент показывает, происходит переоценка или недооценка уровня потерь.
Все вышеуказанные метрики качества подробно описаны под катом.
Подробнее о метриках
PSI используется для проверки данных на репрезентативность и рассчитывается по формуле:
 где — доля наблюдений с -м значением фактора, — количество наблюдений, соответствующих -му значению фактора, — общее количество наблюдений в выборке ( — валидационная выборка, — выборка для разработки).
где — доля наблюдений с -м значением фактора, — количество наблюдений, соответствующих -му значению фактора, — общее количество наблюдений в выборке ( — валидационная выборка, — выборка для разработки).
Обычно используются следующие пороги:
Коэффициент Джини — один из наиболее часто используемых тестов для оценки предсказательной силы факторов и дискриминационной способности модели в целом.
Коэффициент Джини для фактора рассчитывается по следующей формуле:
 где — кумулятивная доля всех наблюдений в группе , — кумулятивная доля целевых событий (target = 1) в группе . Расчет кумулятивных долей проводится в порядке убывания значения целевой переменной.
где — кумулятивная доля всех наблюдений в группе , — кумулятивная доля целевых событий (target = 1) в группе . Расчет кумулятивных долей проводится в порядке убывания значения целевой переменной.
Формула расчета коэффициента Джини для модели LGD:
 где — площадь, ограниченная CAP-кривой тестируемой модели и случайной модели, — площадь, ограниченная CAP-кривой идеальной модели и случайной модели.
где — площадь, ограниченная CAP-кривой тестируемой модели и случайной модели, — площадь, ограниченная CAP-кривой идеальной модели и случайной модели.
Вычисление площадей CAP-кривых в контексте модели LGD производится по следующему алгоритму. Выборка для расчета коэффициента Джини, содержащая фактические и модельные значение LGD, а также соответствующие им значения баланса (основной долг и просроченный основной долг), сортируется по убыванию модельных значений LGD. Затем для каждого смоделированного значения рассчитывается функция:
 где — -ое значение фактического LGD, — соответствующие ему значение баланса, — размер выборки.
где — -ое значение фактического LGD, — соответствующие ему значение баланса, — размер выборки.
Формула для вычисления площади, ограниченной CAP-кривой идеальной модели и случайной модели, имеет следующий вид:
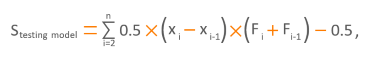 где — накопленный процент всех наблюдений. Площадь, ограниченная CAP-кривой тестируемой модели и случайной модели, вычисляется аналогично с заменой значений фактического на модельное в формуле для .
где — накопленный процент всех наблюдений. Площадь, ограниченная CAP-кривой тестируемой модели и случайной модели, вычисляется аналогично с заменой значений фактического на модельное в формуле для .
Для интуиции — чем выше индекс, тем лучше статистическое качество модели. В качестве ориентира по порогам можно использовать следующие значения: 0,3–0,4 — модель может использоваться для расчетов и оценок, 0,5–0,7 — модели с хорошим качеством, можно делать расчеты и автоматизировать процесс, выше 0,7–0,8 — очень хорошо. В последнем случае рекомендуем перепроверить на предмет лика в данных и ошибках в сборе атрибутов (смотрят в будущее).
Loss-shortfall показывает, насколько общие фактические потери превышают общие смоделированные потери. Потери определяются как произведение LGD (фактических или смоделированных) на соответствующий им баланс (основной долг и просроченный основной долг). Формула для вычисления Loss-shortfall имеет вид:
 где и — смоделированное и фактическое значение средневзвешенного по балансу LGD в бакете просрочки соответственно, — суммарный баланс в бакете , — общее количество бакетов просрочки.
где и — смоделированное и фактическое значение средневзвешенного по балансу LGD в бакете просрочки соответственно, — суммарный баланс в бакете , — общее количество бакетов просрочки.
Доверительные интервалы для теста не рассчитываются. Модель принимается, если фактические потери не превышают смоделированные — .
PSI (population stability index, индекс стабильности популяции)
PSI используется для проверки данных на репрезентативность и рассчитывается по формуле:


Обычно используются следующие пороги:
- до 10% — изменения в распределении минимальны;
- 10–25% — изменения в атрибуте существенны, но не блокируют включение в модель (часто делают так, чтобы эффективный вес таких атрибутов не превышал в итоговой модели 20–30%). Дополнительно эти атрибуты более тщательно мониторятся и валидируются при применении;
- > 25% — данные атрибуты нецелесообразно включать в финальную модель.
G (коэффициент Джини)
Коэффициент Джини — один из наиболее часто используемых тестов для оценки предсказательной силы факторов и дискриминационной способности модели в целом.
Коэффициент Джини для фактора рассчитывается по следующей формуле:

Формула расчета коэффициента Джини для модели LGD:

Вычисление площадей CAP-кривых в контексте модели LGD производится по следующему алгоритму. Выборка для расчета коэффициента Джини, содержащая фактические и модельные значение LGD, а также соответствующие им значения баланса (основной долг и просроченный основной долг), сортируется по убыванию модельных значений LGD. Затем для каждого смоделированного значения рассчитывается функция:

Формула для вычисления площади, ограниченной CAP-кривой идеальной модели и случайной модели, имеет следующий вид:
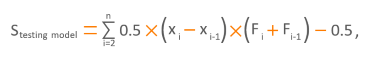
Для интуиции — чем выше индекс, тем лучше статистическое качество модели. В качестве ориентира по порогам можно использовать следующие значения: 0,3–0,4 — модель может использоваться для расчетов и оценок, 0,5–0,7 — модели с хорошим качеством, можно делать расчеты и автоматизировать процесс, выше 0,7–0,8 — очень хорошо. В последнем случае рекомендуем перепроверить на предмет лика в данных и ошибках в сборе атрибутов (смотрят в будущее).
Loss-shortfall
Loss-shortfall показывает, насколько общие фактические потери превышают общие смоделированные потери. Потери определяются как произведение LGD (фактических или смоделированных) на соответствующий им баланс (основной долг и просроченный основной долг). Формула для вычисления Loss-shortfall имеет вид:

Доверительные интервалы для теста не рассчитываются. Модель принимается, если фактические потери не превышают смоделированные — .
Валидация на non-default сегменте
Интегральная оценка качества
Идея данного подхода к валидации состоит в следующем: средний уровень LGD по договорам на первом месяце в дефолте (LGD default) должен соответствовать взвешенному по PD среднему LGD по этим же договорам до наступления дефолта (LGD non-default). Чтобы рассчитать интегральную оценку, необходимы:
- PD и LGD non-default по договорам, которые на данный момент не находятся в состоянии дефолта;
- LGD default по тем же договорам, но по их состоянию на первом месяце после выхода в дефолт;
- фактического среднего LGD по тем же договорам;
- сравнение среднего LGD default со средневзвешенным LGD non-default по PD и со средним фактическим LGD.
Этот алгоритм можно записать формулой:

Матрица сопряженности
Матрица сопряженности уточняет интегральную оценку (табл.). Алгоритм формирования матрицы:
- LGD договоров non-default сегмента делится на бины (например, с шагом 5%);
- далее для этих договоров рассчитывается их LGD на первом месяце в дефолте;
- рассчитанные числа заносятся в таблицу, которая именуется матрицей сопряженности.
Таблица. Пример матрицы сопряженности по LGD non-default и LGD default
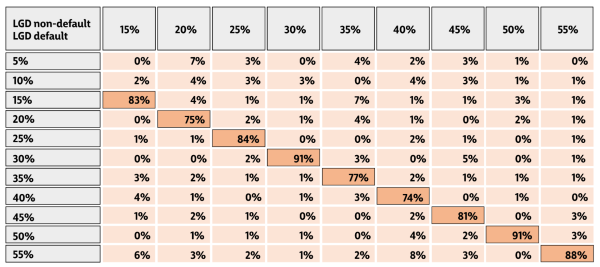
По рассчитанной матрице сопряженности можно судить о разбросе LGD non-default по отношению к LGD, рассчитанному после выхода договора в дефолт. Например, в приведенной таблице видно, что большая часть наблюдений имеет одинаковый LGD по non-default модели и по default модели. Для наглядности, эти ячейки выделены ярким цветом.
Заключение
В заключение, еще раз рассмотрим основные пункты данной статьи.
- При моделировании LGD сначала важно определиться с алгоритмом расчета LGD и выделить сегмент выборки, на котором будет проводиться моделирование.
- Далее желательно провалидировать рассчитанное целевое событие, построив распределения LGD по dpd и default age.
- После этого, в зависимости от доступной информации о договорах и клиентах, собрать предикторы будущей модели LGD.
- На основе распределений LGD по dpd и default age нужно выбрать подходящий алгоритм для моделирования и построить модель LGD.
- Нужно проверить качество и стабильность модели, а также адекватность ее оценок риска на non-default сегменте.
При выполнении этих пяти шагов, можно быть уверенным, что полученная модель является оптимальным вариантом, удовлетворяющим высоким требованиям качества моделей риска и будет корректной с точки зрения бизнеса.
Авторы статьи: Александр Бородин (abv_gbc), Иван Аникин (ivanikin)
Список использованных терминов и сокращений
Введем необходимые определения.
- Дефолт – это невыполнение обязательств по договору займа. Обычно, дефолтом считается неоплата по договору в течение 90 дней.
- Выздоровление – процесс выхода из дефолта. Клиент не платил по обязательствам в течение 90 дней, был зафиксирован дефолт, но потом все же клиент внес средства на счет. Обычно выздоровлением считается снижение просрочки по платежам после наступления дефолта до 30 и менее дней. После выздоровления возможны повторные дефолты.
- PD – probability of default – вероятность дефолта.
- EAD – exposure at default – кредитные обязательства по договору на момент дефолта. По сути, баланс на дату дефолта, где баланс = Тело долга + Просрочка.
- LGD – loss given default – доля EAD, которую клиент не возвращает на горизонте восстановления.
- EL – expected loss – ожидаемые потери по договору.
- Default сегмент – это набор договоров, которые находятся в состоянии дефолта на дату наблюдения.
- Non-default сегмент – это набор договоров, которые не находятся в состоянии дефолта на дату наблюдения, но на горизонте наблюдения (горизонт PD) уйдут хотя бы один раз в дефолт.
- Дата наблюдения – это дата, на которую собираются атрибуты по состоянию договора, а также относительно которой начинается горизонт сбора целевого события.
Ссылки
[1] ML и DS оттенки кредитного риск-менеджмента
[2] ML и DS оттенки кредитного риск-менеджмента | Компоненты
[3] ML и DS оттенки кредитного риск-менеджмента | EAD или деньги в дефолте
[4] Dahlin F., Storkitt S. Estimation of loss given default for low default portfolios. – 2014.
[5] Anderson D. et al. A Practitioner’s Guide to Generalized Linear Models—a foundation for theory, interpretation and application. – 2007
[6] Creating Interval Target Scorecards with Credit Scoring for SAS Enterprise Miner

