Гистограммам не чужды систематические ошибки. Дело в том, что они достаточно условны и могут привести к неправильным выводам о данных. Если вы хотите визуализировать переменную, лучше выбрать другой график.

Независимо от того, находитесь ли вы на встрече с высшим руководящим составом или со специалистами по обработке данных, в одном вы можете быть уверены: в какой-то момент появится гистограмма.

И нетрудно догадаться почему. Гистограммы весьма интуитивно наглядны: любой поймет их с первого взгляда. Более того, они объективно представляют реальность, не так ли? А вот и нет.

Гистограмма может ввести в заблуждение и привести к ошибочным выводам — ??даже на простейшем наборе данных!

В этой статье мы на примерах рассмотрим 6 причин, почему, когда дело доходит до визуализации данных, гистограммы точно не является лучшим выбором:

1. Они слишком сильно зависят от количества интервалов.

2. Они слишком сильно зависят от максимума и минимума переменной.

3. Они не дают возможности заметить значимые значения переменной.

4. Они не позволяют отличить непрерывные переменные от дискретных.

5. Они делают сравнение распределений сложным.

6. Их построение затруднено, если в памяти находятся не все данные.

«Ладно, я понял: гистограммы не идеальны. Но есть ли у меня выбор?» Конечно есть!

В конце статьи я порекомендую другой график, называемый CDP, который минует эти недостатки.

Итак, что же не так с гистограммой?

1. Она слишком сильно зависит от количества интервалов.

Чтобы построить гистограмму, вы должны сначала определить количество интервалов, также называемых корзинами (bins). Для этого существует множество различных практических методов (вы можете ознакомиться с их обзором на этой странице). Но насколько критичен этот выбор? Давайте возьмем реальные данные и посмотрим, как меняется гистограмма в зависимости от количества интервалов.

Переменная представляет собой максимальную частоту сердечных сокращений (ударов в минуту), полученную у 303 людей во время некоторой физической активности (данные взяты из набора данных UCI по сердечным заболеваниям: источник).

Глядя на верхний левый график (который мы получим по умолчанию в Python и R), у нас сложится впечатление хорошего распределения с одним пиком (модой). Однако если бы мы рассмотрели бы другие варианты гистограммы, мы получили бы совершенно другую картину. Разные гистограммы одних и тех же данных могут привести к противоречивым выводам.

2. Она слишком сильно зависит от максимума и минимума переменной.

Даже после того, как количество интервалов установлено, интервалы зависят от положения минимума и максимума переменной. Достаточно, чтобы один из них немного изменился, и все интервалы также изменятся. Другими словами, гистограммы не являются надежными.

Например, давайте попробуем изменить максимум переменной, не меняя количество интервалов.

Отличается только одно значение, а весь график получается другим. Это нежелательное свойство, потому что нас интересует общее распределение: одно значение не должно так влиять на график!

3. Не дает возможности заметить значимые значения переменной.

Если в общем, то когда переменная содержит некоторые часто повторяющиеся значения, нам конечно нужно об этом знать. Однако гистограммы этому препятствуют, поскольку они основаны на интервалах, а интервалы «скрывают» отдельные значения.

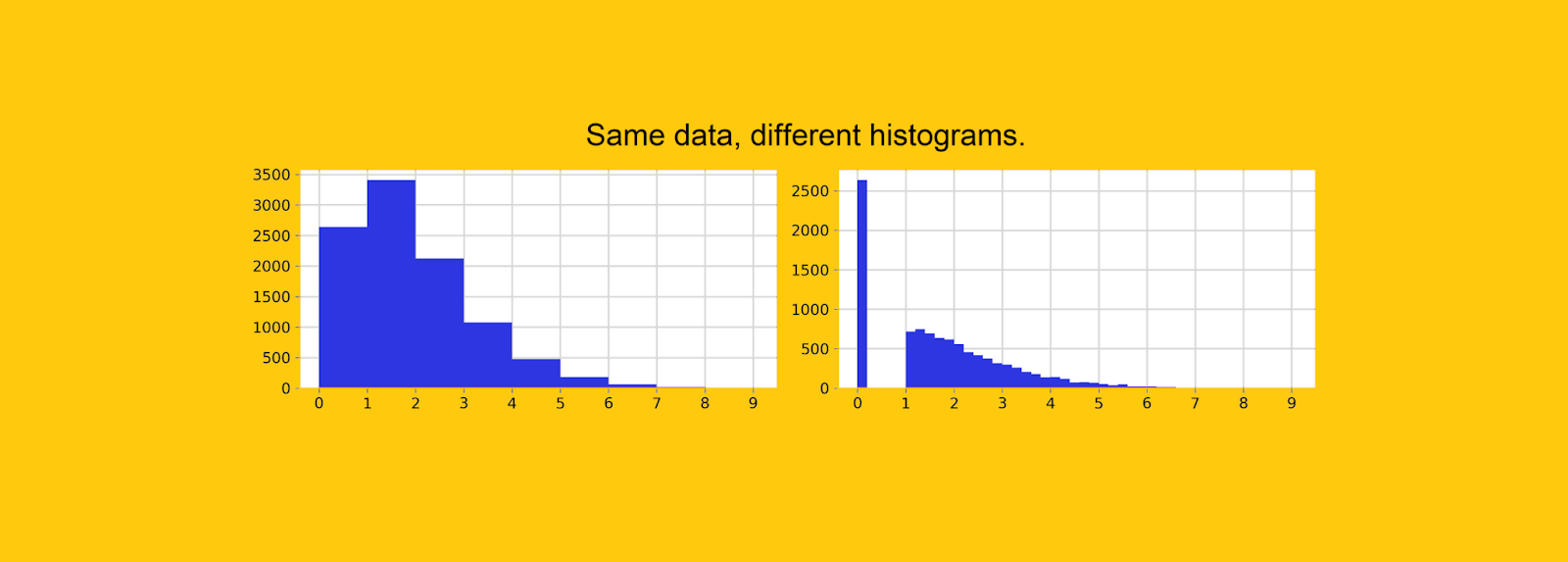
Классическим примером является случай, когда отсутствующим значениям массово присваивается 0. В качестве примера давайте рассмотрим набор данных переменной, состоящий из 10 тысяч значений, 26% из которых — нули.

График слева — это то, что вы получаете по умолчанию в Python. Глядя на него, вы не заметите скопление нулей, и вы даже можете подумать, что эта переменная имеет «плавную» динамику.

График справа получен путем сужения интервалов и дает более четкое представление о реальности. Но дело в том, что как бы вы ни сужали интервалы, вы никогда не будете уверены, содержит ли первый интервал только 0 или какие-то другие значения.

4. Не позволяет отличить непрерывные переменные от дискретных.

Зачастую мы бы хотели знать, является ли числовая переменная непрерывной или дискретной. По гистограмме это практически невозможно сказать.

Возьмем переменную «Возраст» (Age). Вы можете получить Возраст = 49 лет (когда возраст округлен) или Возраст = 49,828884325804246 лет (когда возраст рассчитывается как количество дней с момента рождения, деленное на 365,25). Первая — дискретная переменная, вторая — непрерывная.

Тот, что слева, непрерывен, а тот, что справа, дискретен. Однако на верхних графиках (по умолчанию в Python) вы не увидите никакой разницы между ними: они выглядят совершенно одинаково.

5. Сложно сравнивать распределения.

Часто бывает необходимо сравнить одну и ту же переменную в разных кластерах. Например, в отношении данных UCI о сердечных заболеваниях, приведенных выше, мы можем сравнить:

• все население (для справки)

• люди моложе 50 страдающие сердечными заболеваниями

• люди моложе 50 НЕ страдающие сердечными заболеваниями

• люди старше 60 лет страдающие сердечными заболеваниями

• люди старше 60 и НЕ страдающие сердечными заболеваниями.

Вот что мы получили бы в итоге:

Гистограммы основаны на областях, и, когда мы пытаемся провести сравнение, области в конечном итоге перекрываются, что делает эту задачу практически невыполнимой.

6. Сложно построить, если в памяти находятся не все данные.

Если все ваши данные находятся в Excel, R или Python, построить гистограмму легко: в Excel вам просто нужно кликнуть по иконке гистограммы, в R — выполнить команду hist(x), а в Python — plt.hist(х).

Но предположим, что ваши данные хранятся в базе данных. Вы же не хотите выгружать все данные только для того, чтобы построить гистограмму, верно? По сути, все, что вам нужно, это таблица, содержащая для каждого интервала крайние значения и количество наблюдений. Примерно такая:

| INTERVAL_LEFT | INTERVAL_RIGHT | COUNT         |

|---------------|----------------|---------------|

| 75.0          | 87.0           | 31            |

| 87.0          | 99.0           | 52            |

| 99.0          | 111.0          | 76            |

| ...           | ...            | ...           |

Но получить ее с помощью SQL-запроса не так просто, как кажется. Например, в Google Big Query код будет выглядеть так:

WITH
STATS AS (
  SELECT 
    COUNT(*) AS N,
    APPROX_QUANTILES(VARIABLE_NAME, 4) AS QUARTILES
  FROM
    TABLE_NAME
),
BIN_WIDTH AS (
  SELECT
    -- freedman-diaconis formula for calculating the bin width
    (QUARTILES[OFFSET(4)] — QUARTILES[OFFSET(0)]) / ROUND((QUARTILES[OFFSET(4)] — QUARTILES[OFFSET(0)]) / (2 * (QUARTILES[OFFSET(3)] — QUARTILES[OFFSET(1)]) / POW(N, 1/3)) + .5) AS FD
  FROM 
    STATS
),
HIST AS (
  SELECT 
    FLOOR((TABLE_NAME.VARIABLE_NAME — STATS.QUARTILES[OFFSET(0)]) / BIN_WIDTH.FD) AS INTERVAL_ID,
    COUNT(*) AS COUNT
  FROM 
    TABLE_NAME,
    STATS,
    BIN_WIDTH
  GROUP BY 
    1
)
SELECT 
  STATS.QUARTILES[OFFSET(0)] + BIN_WIDTH.FD * HIST.INTERVAL_ID AS INTERVAL_LEFT,
  STATS.QUARTILES[OFFSET(0)] + BIN_WIDTH.FD * (HIST.INTERVAL_ID + 1) AS INTERVAL_RIGHT,
  HIST.COUNT
FROM 
  HIST, 
  STATS, 
  BIN_WIDTH

Немного громоздко, не правда ли?

Альтернатива: график кумулятивного распределения.

Узнав 6 причин, по которым гистограмма не является идеальным выбором, возникает естественный вопрос: «Есть ли у меня альтернатива?» Хорошие новости: существует лучшая альтернатива, которая называется «График кумулятивного распределения» (Cumulative Distribution Plot - CDP). Я знаю, что это название не такое запоминающееся, но гарантирую, оно того стоит.

График кумулятивного распределения — это график квантилей переменной. Другими словами, каждая точка CDP показывает:

• по оси x: исходное значение переменной (как в гистограмме);

• по оси y: сколько наблюдений имеют такое же или меньшее значение.

Давайте посмотрим на пример с переменной — максимальной частотой пульса.

Возьмем точку с координатами x = 140 и y = 90 (30%). По горизонтальной оси вы видите значение переменной: 140 ударов сердца в минуту. По вертикальной оси вы видите количество наблюдений, у которых частота сердцебиение равна или ниже 140 (в данном случае 90 человек, что означает 30% выборки). Следовательно, у 30% нашей выборки максимальная частота сердцебиения составляет 140 или менее ударов в минуту.

Какой смысл в графике, показывающем, сколько наблюдений «равно или ниже» заданного уровня? Почему не просто «равно»? Потому что в противном случае результат зависел бы от отдельных значений переменной. И это не сработает, потому что каждое значение имеет очень мало наблюдений (обычно только одно, если переменная непрерывна). Напротив, CDP полагаются на квантили, которые более стабильны, выразительны и легко читаются.

Вдобавок CDP намного полезнее. Если задуматься, вам часто приходится отвечать на такие вопросы, как «у скольких из них от 140 до 160?» Или «у скольких из них больше 180?». Имея перед глазами CDP, вы можете дать немедленный ответ. С гистограммой это было бы невозможно.

CDP решает все проблемы, которые мы видели выше. Фактически, по сравнению с гистограммой:

1. Не требует пользовательского выбора. Для одного набора данных, существует только один возможный CDP.

2. Не страдает от выпадающих значений. Экстремальные значения не влияют на CDP, поскольку квантили не меняются.

3. Позволяет определять значимые значения. Если существует концентрация точек данных на каком-то конкретном значении, это сразу видно, поскольку будет вертикальный сегмент, соответствующий значению.

4. Позволяет с первого взгляда распознать дискретную переменную. Если существует только конкретный набор возможных значений (т.е. переменная дискретна), это сразу видно, поскольку кривая примет форму лестницы.

5. Упрощает сравнение распределений. На одном графике легко сравнить два или более распределения, поскольку это просто кривые, а не области. Кроме того, ось y всегда находится в диапазоне от 0 до 100%, что делает сравнение еще более простым. Для сравнения, это пример, который мы видели выше:

6. Его легко построить, даже если у вас нет всех данных в памяти. Все, что вам нужно, это квантили, которые можно легко получить с помощью SQL:

SELECT 
  COUNT(*) AS N,
  APPROX_QUANTILES(VARIABLE_NAME, 100) AS PERCENTILES
FROM
  TABLE_NAME

Как построить график кумулятивного распределения в Excel, R, Python

В Excel вам нужно построить два столбца. Первый с 101 числом, равномерно распределенными от 0 до 1. Второй столбец должен содержать процентили, которые могут быть получены по формуле: =PERCENTILE(DATA, FRAC), где DATA - это вектор, содержащий данные, а FRAC - это первый столбец: 0,00, 0,01, 0,02, 0,03,…, 0,98, 0,99, 1. Затем вам просто нужно построить график по этим двум столбцам, разместив значения переменной на оси x.

В R это делается в одну строчку:

plot(ecdf(data))

В Python:

from statsmodels.distributions.empirical_distribution import ECDF
import matplotlib.pyplot as plt
ecdf = ECDF(data)
plt.plot(ecdf.x, ecdf.y)

Спасибо за внимание! Надеюсь, эта статья оказалась для вас полезной.

Я ценю отзывы и конструктивную критику. Если вы хотите поговорить об этой статье или других связанных темах, вы можете написать мне в Linkedin.

Перевод материала подготовлен в рамках онлайн-курса "Machine Learning. Basic". Всех заинтересованных приглашаем на день открытых дверей курса, где можно будет узнать все подробности об обучении и пообщаться с преподавателем.

- Узнать подробнее о курсе "Machine Learning. Basic"

- Смотреть онлайн-встречу "День открытых дверей"