Методы градиента политики PG довольно популярны в обучении с подкреплением (RL). Базовый принцип состоит в использовании градиентного спуска и подъема в направлениях, где ожидается наибольшая награда. Но при первом приближении оптимизация получается неаккуратной. При чрезмерной самоуверенности мы можем сделать действия, которые разрушат прогресс, достигнутый предыдущей тренировкой. Работы, посвященные TRPO, являются наиболее цитируемыми по этой проблеме. При этом его объясняют без должного введения в три базовые концепции: MM алгоритм, регион доверия и выборка по значимости (перенормировка).

В RL мы оптимизируем функцию политики, чтобы получать максимальное дисконтированное вознаграждение. Тем не менее есть несколько сложностей, которые вредят.

Первая сложность в том, то PG использует самый крутой спуск по направлению к большему вознаграждению и соответственно делает шаг в этом направлении.

Этот метод использует только первую производную и думает, что поверхность плоская. Если же поверхность изогнутая, то мы можем зайти не туда.

Слишком большие шаги ведут к катастрофе, а слишком маленькие тормозят обучения. Можно изобразить поверхность функции вознаграждения, как скалу. Если путник сделает слишком большой шаг возле обрыва, то он упадет вниз к меньшим показателям. Если мы продолжим с места падения, то займет много времени на восстановление достигнутых ранее показателей.

Во-вторых, очень трудно узнать правильную скорость обучения (learning rate). Допустим скорость обучения хорошо настроена в желтой точке. Эта область относительно плоская и скорость обучения должна быть выше, чем средняя. Но после неверного шага мы падаем вниз к красной точке. Градиент в этой точке высок и эта скорость обучения приведет к взрыву градиента. Так как скорость обучение не чувствительная к рельефу, то PG будет в таких случаях иметь плохую сходимость. Небольшие изменения в параметрах могут привести к заметным изменениям в политике . Небольшие изменения в политике ведут в большим изменениям в вознаграждении. Надо как-то сделать так, чтобы вознаграждение было под контролем…
В третьих, стоит вопрос,- а надо ли еще ограничивать изменения политики, чтобы не совершать шальных шагов? На самом деле это то, то делает TRPO. Под контроль берутся как изменения в политике, так и изменения в вознаграждении. Этот алгоритм ограничивает изменения параметров в соответствии с конъюнктурой поверхности, чтобы не сильно изменять политику и вознаграждение на каждом шаге. Но рецепт, как это сделать совсем неочевиден. Мы вводим дополнительные параметры.
В четвертых, мы должны использовать всю траекторию(т.е. массив состояний среды и реакций агента) для одного изменения политики. То есть мы не можем изменять политику на каждом шаге траектории.

Почему? Визуализируем модель политики, как сеть. Увеличение вероятности в одной точке. Тянет за собой близлежащие точки тоже. Состояния внутри траекторий очень похожи в частности, когда они представлены сырыми пикселями. Если мы обновляем политику на каждом шагу, то мы тянем близлежащие точки много раз. Изменения усиливают друг друга и делаю процесс тренировки нестабильным.

В одной траектории может быть сотни или тысячи шагов. Одно обновление для каждой траектории не репрезентативно, поэтому используется много траекторий. В простом PG требуется порядка 10 миллионов или больше шагов для обучения даже в небольших экспериментах. То есть выборка обучающих примеров работает мало эффективно. Для того, чтобы обучить реального робота потребуются слишком большие затраты для этого, так как скорее робот изотрётся в порошок, чем чему-нибудь научится.
Кратко сформулируем недостатки PG
Можем ли мы гарантировать, что любые изменения политики неуклонно увеличивают ожидаемое вознаграждение? Кажется, что это нереально, но теоретически возможно. В MM алгоритме это достигается интерактивно с помощью максимизации суррогатных функций . Эти функции во всех точках меньше, чем исходная функция. Звучит тавтологически.
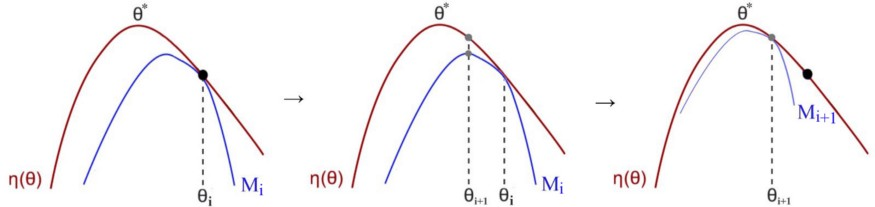
Попробуем разобраться в деталях. Мы сначала стартуем с некой приближенной политики. Мы находим суррогатную функию , которая аппроксимирует вознаграждение локально в текущем предположении. На функции мы находим точку максимума и перемещаем параметры политики в эту точку и тд.
Для будущих выкладок, пусть является квадратичной функцией.
, что в векторной форме выглядит так:
функция выпуклая и поэтому хорошо известно, как её оптимизировать.
Суррогатную квадратичную функцию легко построить через разложение в ряд Тэйлора до второго члена и немного модифицировав второй член, умножив его на определенный множитель.
Почему MM алгоритм сходится к оптимальной политике?
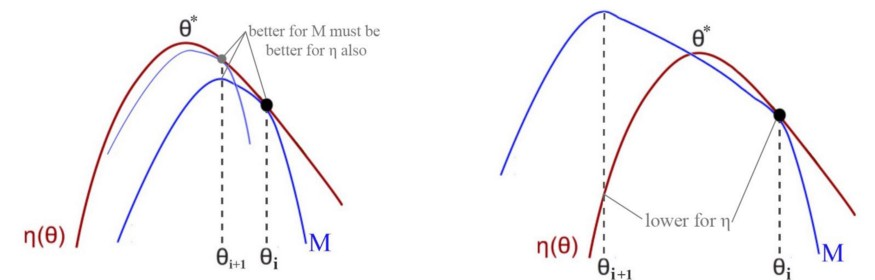
Если M является нижней границей, то она никогда не пересекает красную линию. И если рассуждать от обратного, то предположим, что ожидаемое вознаграждение уменьшается, тогда красная линия пересекает синюю и это противоречит тому, что M является нижней границей.
Так как мы имеем ограниченные политики, то по мере продвижения мы интерактивно будем приближаться к глобальному максимуму, то есть к оптимальной политике. Так мы находим магию, которая нам нужна.
angms.science/doc/NMF/Surrogate.pdf
www.leg.ufpr.br/~paulojus/EM/Tutorial%20on%20MM.pdf
(Примечание переводчика: для разложения в ряд Тэйлора до второго члена потребуется знание этой матрицы en.wikipedia.org/wiki/Hessian_matrix)
В математике есть два метода оптимизации: через линейный поиск и через доверительный регион. Градиентный спуск является примером линейного поиском. Мы сначала определяем направление спуска, а потом делаем шаг в этом направлении.

В методе доверительного региона мы сначала определяем максимальный размер шага и далее ищем оптимальную точку внутри региона. Давайте начнём с начальной точки, определим размер шага ?, как радиус доверительного региона (желтый круг).
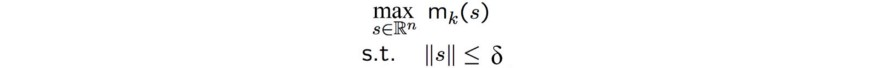
В этой формуле m является приближением нашей исходной функции f. Нашей целью является поиск оптимальной точки для m внутри радиуса ?. Мы продолжаем процесс интерактивно, пока не приблизимся к пику с достаточной точностью.

Чтобы лучше контролировать процесс обучения, мы можем динамически увеличивать или уменьшать ? в соответствии с изогнутостью поверхности. В традиционном методе доверительного региона ? уменьшается, если аппроксиматор плохо аппроксимирует исходную функцию и наоборот при хорошей аппроксимации — ? увеличивается. Но вычислить f в случае RL довольно трудно. Вместо этого используется альтернативный способ, — мы уменьшаем шаг ?, если вдруг заметили, что расхождение текущей политики и политики предыдущего шага стали слишком большими. И наоборот. То есть, чтобы более осторожно шагать, мы уменьшаем регион доверия, если политика стала изменяться слишком быстро.
Выборка по значимости – это техника оценки параметров распределения, если мы имеем выборку из другого, функционально зависимого распределения. Выборка по значимости вычисляет ожидаемое значение , где распределено по .

Тут мы предлагаем не создавать выборку и не получать серию конкретных значений . Вместо этого мы делаем рекалибровку между двумя распределениями. Таким образом мы можем использовать примеры из старой политики, чтобы получить градиент в новой точке.

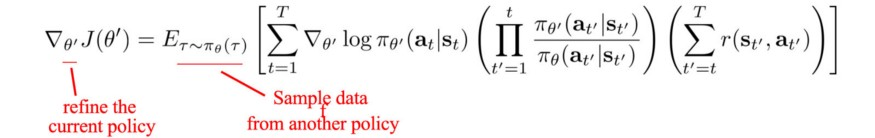
Такой трюк возможен, если старая и новая политики мало отличаются, так как в противном случае использование примеров из другой политики делает процесс сходимости менее стабильным.
Более подробно процесс разобран в
rail.eecs.berkeley.edu/deeprlcourse-fa17/f17docs/lecture_13_advanced_pg.pdf
Тем не менее мы не можем слишком долго использовать примеры из одной и той же политики. Нам все равно необходимо перевычислять траектории довольно часто с использованием текущей политики. Но мы можем это делать не каждый раз, а, например, один раз в 4 итерации. То есть мы получаем обучающие примеры и аккуратно двигаемся несколько итераций в сторону увеличения вознаграждения. Это движение не обязательно будет прямым.
Разберем детально, как использовать выборку по значимости применительно к PG.
Если изначальная формулировка выглядит так:
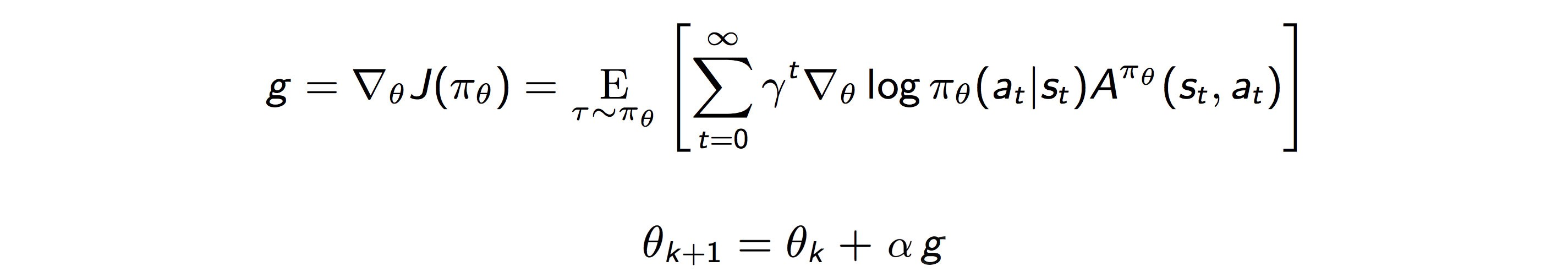
Попробуем записать по-другому при условии, что часто ?=1.
Мы можем обратить производные и получить
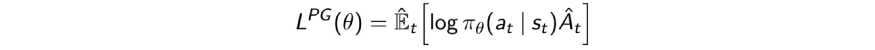
Это может быть выражено как
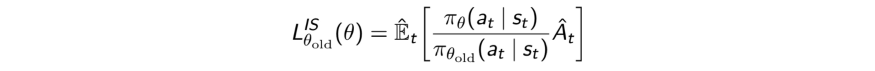
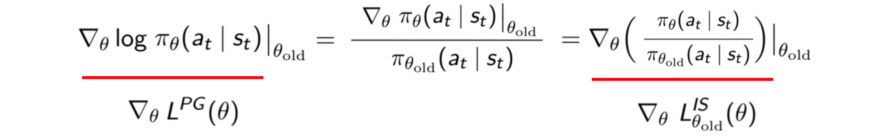
Так как производные обоих целевых функций одинаковы, то и оптимальное решение тоже одинаково.
Присутствие двух политик в процессе оптимизации позволяет формально ограничивать изменения в политике. Это ключевой принцип для многих PG методов. Так же это позволяет оценить новую политику прежде, чем принять изменение.
И так мы описали три базовые концепции, и готовы погрузиться в TRPO.

Трудности метода градиента политики (PG)
В RL мы оптимизируем функцию политики, чтобы получать максимальное дисконтированное вознаграждение. Тем не менее есть несколько сложностей, которые вредят.

Первая сложность в том, то PG использует самый крутой спуск по направлению к большему вознаграждению и соответственно делает шаг в этом направлении.

Этот метод использует только первую производную и думает, что поверхность плоская. Если же поверхность изогнутая, то мы можем зайти не туда.

Слишком большие шаги ведут к катастрофе, а слишком маленькие тормозят обучения. Можно изобразить поверхность функции вознаграждения, как скалу. Если путник сделает слишком большой шаг возле обрыва, то он упадет вниз к меньшим показателям. Если мы продолжим с места падения, то займет много времени на восстановление достигнутых ранее показателей.

Во-вторых, очень трудно узнать правильную скорость обучения (learning rate). Допустим скорость обучения хорошо настроена в желтой точке. Эта область относительно плоская и скорость обучения должна быть выше, чем средняя. Но после неверного шага мы падаем вниз к красной точке. Градиент в этой точке высок и эта скорость обучения приведет к взрыву градиента. Так как скорость обучение не чувствительная к рельефу, то PG будет в таких случаях иметь плохую сходимость. Небольшие изменения в параметрах могут привести к заметным изменениям в политике . Небольшие изменения в политике ведут в большим изменениям в вознаграждении. Надо как-то сделать так, чтобы вознаграждение было под контролем…
В третьих, стоит вопрос,- а надо ли еще ограничивать изменения политики, чтобы не совершать шальных шагов? На самом деле это то, то делает TRPO. Под контроль берутся как изменения в политике, так и изменения в вознаграждении. Этот алгоритм ограничивает изменения параметров в соответствии с конъюнктурой поверхности, чтобы не сильно изменять политику и вознаграждение на каждом шаге. Но рецепт, как это сделать совсем неочевиден. Мы вводим дополнительные параметры.
В четвертых, мы должны использовать всю траекторию(т.е. массив состояний среды и реакций агента) для одного изменения политики. То есть мы не можем изменять политику на каждом шаге траектории.

Почему? Визуализируем модель политики, как сеть. Увеличение вероятности в одной точке. Тянет за собой близлежащие точки тоже. Состояния внутри траекторий очень похожи в частности, когда они представлены сырыми пикселями. Если мы обновляем политику на каждом шагу, то мы тянем близлежащие точки много раз. Изменения усиливают друг друга и делаю процесс тренировки нестабильным.

В одной траектории может быть сотни или тысячи шагов. Одно обновление для каждой траектории не репрезентативно, поэтому используется много траекторий. В простом PG требуется порядка 10 миллионов или больше шагов для обучения даже в небольших экспериментах. То есть выборка обучающих примеров работает мало эффективно. Для того, чтобы обучить реального робота потребуются слишком большие затраты для этого, так как скорее робот изотрётся в порошок, чем чему-нибудь научится.
Кратко сформулируем недостатки PG
- Слишком большие изменения в политике разрушают тренировку.
- еверная скорость обучения ведет к исчезающим или взрывным градиентам
- Нет прямой связи между величиной изменения параметров модели и величиной изменения политики.
- Низкая эффективность использования выборки обучающих примеров.
Алгоритм миноризации максимизации
Можем ли мы гарантировать, что любые изменения политики неуклонно увеличивают ожидаемое вознаграждение? Кажется, что это нереально, но теоретически возможно. В MM алгоритме это достигается интерактивно с помощью максимизации суррогатных функций . Эти функции во всех точках меньше, чем исходная функция. Звучит тавтологически.

Попробуем разобраться в деталях. Мы сначала стартуем с некой приближенной политики. Мы находим суррогатную функию , которая аппроксимирует вознаграждение локально в текущем предположении. На функции мы находим точку максимума и перемещаем параметры политики в эту точку и тд.
Для будущих выкладок, пусть является квадратичной функцией.
, что в векторной форме выглядит так:
функция выпуклая и поэтому хорошо известно, как её оптимизировать.
Суррогатную квадратичную функцию легко построить через разложение в ряд Тэйлора до второго члена и немного модифицировав второй член, умножив его на определенный множитель.
Почему MM алгоритм сходится к оптимальной политике?

Если M является нижней границей, то она никогда не пересекает красную линию. И если рассуждать от обратного, то предположим, что ожидаемое вознаграждение уменьшается, тогда красная линия пересекает синюю и это противоречит тому, что M является нижней границей.
Так как мы имеем ограниченные политики, то по мере продвижения мы интерактивно будем приближаться к глобальному максимуму, то есть к оптимальной политике. Так мы находим магию, которая нам нужна.
angms.science/doc/NMF/Surrogate.pdf
www.leg.ufpr.br/~paulojus/EM/Tutorial%20on%20MM.pdf
(Примечание переводчика: для разложения в ряд Тэйлора до второго члена потребуется знание этой матрицы en.wikipedia.org/wiki/Hessian_matrix)
Доверительный регион
В математике есть два метода оптимизации: через линейный поиск и через доверительный регион. Градиентный спуск является примером линейного поиском. Мы сначала определяем направление спуска, а потом делаем шаг в этом направлении.

В методе доверительного региона мы сначала определяем максимальный размер шага и далее ищем оптимальную точку внутри региона. Давайте начнём с начальной точки, определим размер шага ?, как радиус доверительного региона (желтый круг).
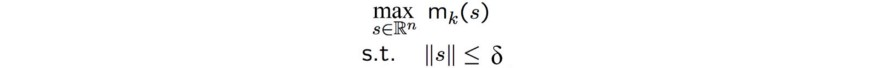
В этой формуле m является приближением нашей исходной функции f. Нашей целью является поиск оптимальной точки для m внутри радиуса ?. Мы продолжаем процесс интерактивно, пока не приблизимся к пику с достаточной точностью.

Чтобы лучше контролировать процесс обучения, мы можем динамически увеличивать или уменьшать ? в соответствии с изогнутостью поверхности. В традиционном методе доверительного региона ? уменьшается, если аппроксиматор плохо аппроксимирует исходную функцию и наоборот при хорошей аппроксимации — ? увеличивается. Но вычислить f в случае RL довольно трудно. Вместо этого используется альтернативный способ, — мы уменьшаем шаг ?, если вдруг заметили, что расхождение текущей политики и политики предыдущего шага стали слишком большими. И наоборот. То есть, чтобы более осторожно шагать, мы уменьшаем регион доверия, если политика стала изменяться слишком быстро.
Выборка по значимости (перенормировка)
Выборка по значимости – это техника оценки параметров распределения, если мы имеем выборку из другого, функционально зависимого распределения. Выборка по значимости вычисляет ожидаемое значение , где распределено по .

Тут мы предлагаем не создавать выборку и не получать серию конкретных значений . Вместо этого мы делаем рекалибровку между двумя распределениями. Таким образом мы можем использовать примеры из старой политики, чтобы получить градиент в новой точке.

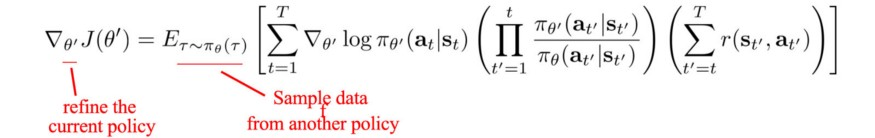
Такой трюк возможен, если старая и новая политики мало отличаются, так как в противном случае использование примеров из другой политики делает процесс сходимости менее стабильным.
Более подробно процесс разобран в
rail.eecs.berkeley.edu/deeprlcourse-fa17/f17docs/lecture_13_advanced_pg.pdf
Тем не менее мы не можем слишком долго использовать примеры из одной и той же политики. Нам все равно необходимо перевычислять траектории довольно часто с использованием текущей политики. Но мы можем это делать не каждый раз, а, например, один раз в 4 итерации. То есть мы получаем обучающие примеры и аккуратно двигаемся несколько итераций в сторону увеличения вознаграждения. Это движение не обязательно будет прямым.
Целевая функция с использованием выборка по значимости(перенормировки)
Разберем детально, как использовать выборку по значимости применительно к PG.
Если изначальная формулировка выглядит так:
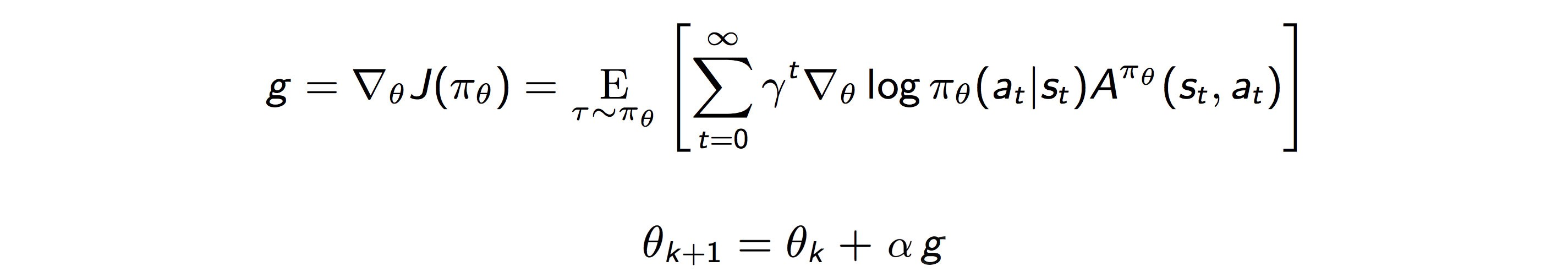
Попробуем записать по-другому при условии, что часто ?=1.
Мы можем обратить производные и получить
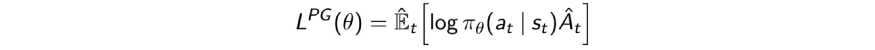
Это может быть выражено как
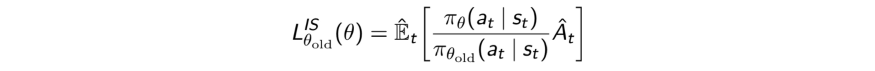
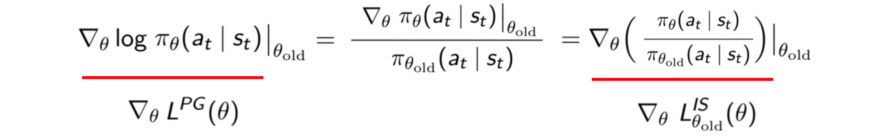
Так как производные обоих целевых функций одинаковы, то и оптимальное решение тоже одинаково.
Присутствие двух политик в процессе оптимизации позволяет формально ограничивать изменения в политике. Это ключевой принцип для многих PG методов. Так же это позволяет оценить новую политику прежде, чем принять изменение.
И так мы описали три базовые концепции, и готовы погрузиться в TRPO.

