23.01.2019 07:11
dim2r 25 5000 Источник
В целом ответ – да. Особенно, когда есть мозги и знание теоремы Байеса.

Напомню, что среднее и дисперсию можно считать только, если у вас имеется определенное количества событий. В старых методичках СССР РТМ (руководящий технический материал) говорилось, что чтобы считать среднее и дисперсию необходимо 29 измерений. Сейчас в ВУЗах немного округлили и используют число 30 измерений. С чем это связано – вопрос философский. Почему я не могу просто взять и посчитать среднее, если у меня есть 5 измерений? По идее ничто не мешает, только среднее получается нестабильным. После еще одного измерения и пересчета оно может сильно измениться и полагаться на него можно начиная где-то с 30 измерений. Но и после 31го измерения оно тоже пошатнется, только уже не так заметно. Плюс добавляется проблема, что и среднее можно считать по разному и получать разные значения. То есть из большой выборки можно выбрать первые 30 и посчитать среднее, потом выбрать другие 30 и тд … и получить много средних, которые тоже можно усреднять. Истинное среднее бывает недостижимо на практике, так как всегда имеем конечное количество измерений. В таком случае среднее является статистической величиной со своим средним и дисперсией. То есть измеряя среднее на практике мы имеем в виду «предположительное среднее», которое может быть близко к идеальному теоретическом значению.

Попробуем разобраться в вопросе, на входе мы имеем некоторое количество фактов и хотим на выходе построить представление об источнике этих фактов. Будем строить мат модель и использовать теорию Байеса для связки модели и фактов.


Рассмотрим уже заезженную модель с ведром, в которое насыпали много черных и белых шаров и тщательно перемешали. Пусть черным соответствует величина 0, а белым 1. Будем их случайно вытаскивать и считать пресловутое среднее значение. По сути это и есть упрошенное измерение, так как назначены числа и поэтому и в данном случае имеется среднее значение измерений, которое зависит от соотношения разных шаров.

Вот тут натыкаемся на интересный момент. Точное соотношение шаров мы можем вычислить при большом количестве измерений. Но если количество измерений мало, то возможны спецэффекты в виде отклонения от статистики. Если в корзине 50 белых и 50 черных шаров, то возникает вопрос — есть ли вероятность вытащить 3 белых шара подряд? И ответ — конечно есть! А если в 90 белых и 10 черных, то эта вероятность повышается. И что думать о содержимом урны, если так повезло, что в самом начале совершенно нечаянно вытащили именно 3 белых шара? – у нас есть варианты.

Очевидно, что получить 3 подряд белых шара равна единице, когда у нас имеется 100% белых шаров. В других случаях эта вероятность меньше. А если все шары черные, то вероятность равна нулю. Попробуем систематизировать эти рассуждения и привести формулы. На помощь приходит метод Байеса, который позволяет ранжировать предположения и давать им числовые значения, определяющие вероятность того, что данное предположение будет соответствовать реальности. То есть перейти от вероятностного истолкования данных к вероятностному истолкованию причин.

Как именно можно численно оценить то или иное предположение? Для этого потребуется модель, в рамках которой мы будем действовать. Слава богу, она простая. Множество предположений о содержимом корзины мы можем записать в виде модели с параметром. В данном случае достаточно одного параметра. Этот параметр по сути задает непрерывный набор предположений. Главное, чтобы он полностью описывал возможные варианты. Двумя крайними вариантами являются, только белые или только черные шары. Остальные случаи где-то посередине.

Допустим, что $\theta$– это доля белых шаров в корзине. Если мы переберем всю корзину и сложим все соответствующие шарам нули и единицы и поделим на общее количество, то $\theta$– будет означать и еще среднее значение наших измерений. $\theta \in [0,1]$. (cейчас $\theta$ часто используется в литературе, как набор свободных параметров, который требует оптимизации).

Самое время перейти к Байесу. Сам Томас Байес заставлял жену случайно бросать мячик, сидя к ней спиной и записывал, как его предположения соотносятся с фактами, куда он полетел на самом деле. Томас Байес пробовал на основе полученных фактов улучшить предсказания следующих бросков. Будем как Томас Байес считать и думать, а спонтанная и непредсказуемая подруга будет вынимать шарики.

Пусть $D$– это массив измерений (data). Используем стандартную запись, где знак $|$ означает вероятность выполнения события слева, если уже известно, что другое событие справа выполнилось. В нашем случае это вероятность получения данных, если известен параметр $\theta$. А так же присутствует случай наоборот — вероятность иметь $\theta$, если известны данные.

$P( \theta | D) = \frac{ P(D | \theta) \cdot P(\theta) }{P(D)}$


Формула Байеса позволяет рассмотреть $\theta$, как случайную величину, и найти наиболее вероятное значение. То есть найти наиболее вероятный коэффициент $\theta$, если он неизвестен.

$\theta = argmax P( \theta | D )$



В правой части имеем 3 члена, которые нужно оценить. Проанализируем их.

1) Требуется знать или вычислить вероятность получения таких данных при той или иной гипотезе $P( D | \theta )$. Получить три белых шара подряд можно, даже если там полно черных. Но наиболее вероятно их получить при большом количестве белых. Вероятность получить белый шар равна $P_{white}=\theta$, а черный $P_{black}=(1-\theta)$. Поэтому если выпало $N$ белых шаров, и $M$ черных шаров, то $P( D | \theta ) = \theta^{N} \cdot (1-\theta)^{M}$. $N$ и $M$ будем считать входными параметрами наших расчетов, а $\theta$ — выходной параметр.

2) Необходимо знать априорную вероятность $P(\theta)$. Вот тут натыкаемся на тонкий момент моделестроения. Мы не знаем эту функцию и будем строить предположения. Если нет дополнительных знаний, то будем считать, что $\theta$ равновероятно в диапазоне от 0 до 1. Если бы мы имели инсайдерскую информацию, то больше знали бы о том, какие значения более вероятны и строили бы более точный прогноз. Но так как такой информации не имеется, то положим $ \theta \sim равномерно[0,1] $. Так как величина $P(\theta)$ не зависит от $\theta$, то при вычислении $\theta$ она не будет иметь значения. $P(\theta)=1$

3) $P(D)$ — это вероятность иметь такой набор данных, если все величины случайны. Мы можем получить данный набор при разных $\theta$ с разной вероятностью. Поэтому учитываются все возможные пути получения набора $D$. Так как на этом этапе еще неизвестно значение $\theta$, то надо проинтегрировать по $P(D) = \int_{0}^{1} P(D|\theta) P(\theta) d\theta $. Чтобы это лучше понять, надо решить элементарные задачи, в которых строится байесовский граф, а потом перейти от суммы к интегралу. Получится такое выражение wolframalpha, которое на поиск максимума $\theta$ не повлияет, так как эта величина не зависит от $\theta$. Результат выражается через факториал для целых значений или в общем случае через гамма функцию.

По сути вероятность той или иной гипотезы пропорциональна вероятности получения набора данных. Другими словами, — при каком раскладе мы скорее всего получим результат, тот расклад и наиболее верный.

Получаем такую формулу

$P( D | \theta) = const \cdot P( \theta | D ) $



Для поиска максимума дифференцируем и приравниваем к нулю:
$0 = \theta^{N-1} \cdot (1-\theta)^{M-1} \cdot (N(\theta-1) + M\theta) $.
Чтобы произведение было равно нулю надо, чтобы один из членов был равен нулю.
Нас не интересуют $\theta=0$ и $\theta=1$, так как в этих точках нет локального максимума, а третий множитель указывает на локальный максимум, поэтому

$\theta=\frac{N}{N+M}$

.

Получаем формулу, которую можно использовать для прогнозов. Если выпало $N$ белых и $M$ черных, то вероятностью $\frac{N}{N+M}$ следующий будет белый. Например было 2 черных и 8 белых, то следующий белый будет с вероятностью 80%.

Желающие могу поиграться с графиком, вводя разные показатели степени:ссылка на wolframalpha.


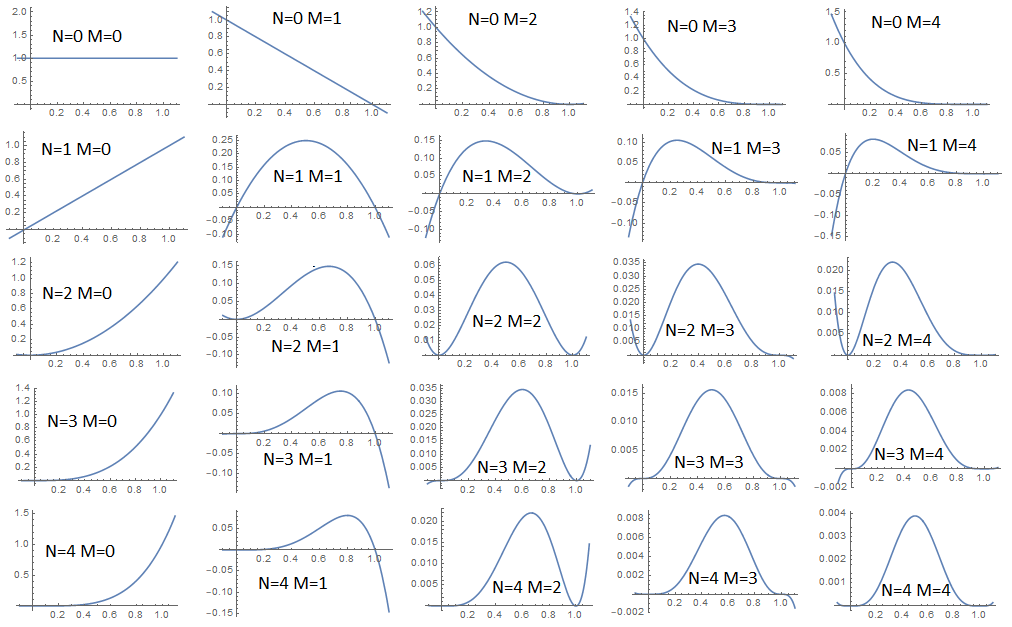
Как видно из графика, единственный случай, когда $P( D | \theta )$ не имеет точечного максимума — это при отсутвии данных $N=0, M=0$. Если же мы имеем хотя бы один факт, то максимум достигается на интервале $[0,1]$ в одной единственной точке. Если $N=0$, то максимум достигается в точке 0, то есть если все шары выпали черные, то скорее всего все остальные шары тоже будут черными и наоборот. Но как уже упоминал, маловероятные комбинации тоже возможны, особенно, если купол нашего распределения пологий. Для того, чтобы оценить однозначность нашего прогноза требуется оценить дисперсию. Уже из графика видно, что при малом количестве фактов дисперсия большая и купол пологий, а при добавлении новых фактов дисперсия уменьшается и купол становится более острым.

Среднее (первый момент) по определению
$\mathbb{M_{1}} = \int_{0}^{1} \theta \cdot P(\theta|D) d\theta $.

По определению дисперсия (второй центральный момент). Его то и будем считать далее в скрытом разделе.
$\mathbb{M_{2}} = \int_{0}^{1} (\theta - \mathbb{M_{1}} )^{2}P(\theta|D) d\theta $.

--- раздел для пытливых умов ---
Давайте получим $P( \theta | D)$ аналитически полностью, если еще не устали. Для этого приведем еще раз все члены из формулы Байеса, включая константные:
$P(\theta)=1$
$P(D) = \int_{0}^{1} P(D|\theta) P(\theta) d\theta = \int_{0}^{1} \theta^{N} \cdot (1-\theta)^{M} d\theta = \frac{N!M!}{(N+M+1)!}$ ссылка на wolframalpha
$P( D | \theta ) = \theta^{N} \cdot (1-\theta)^{M}$

Формула Байеса полностью для нашего случая выглядит так:

$P( \theta | D ) = \theta^{N} \cdot (1-\theta)^{M} \cdot \frac{(N+M+1)!}{N!M!}$



Отсюда среднее после подстановки
$\mathbb{M_{1}} = \int_{0}^{1} \theta \cdot P(\theta|D) d\theta = \int_{0}^{1} \theta \cdot \theta^{N} \cdot (1-\theta)^{M} \cdot (\frac{N!M!}{(N+M+1)!})d\theta = \frac{(N+1)!M!}{(N+M+2)!} \cdot \frac{(N+M+1)!}{N!M!}$.

Используем элементраные знания $(N+1)!=(N+1) \cdot N!$ и сокращая дроби

$\mathbb{M_{1}} =\frac{N+1}{N+M+2} $



Формула первого момента соответствует смыслу эксперимента. При преобладании белых шаров момент уходит в 1, а при преобладании черных стремится к 0. Она даже не капризничает, когда нет шаров, и довольно честно показывает 1/2.

Дисперсия выражается еще формулой, с которой будем работать.
$\mathbb{M_{2}} = \mathbb{M_{1}}(\theta^2) - \mathbb{M_{1}}(\theta)^2 $.
Первый член $\mathbb{M_{1}}(\theta^2) $ по большей части повторяет формулу для $\mathbb{M_{1}}( \theta )$, используется — $\theta^2$
$\mathbb{M_{1}}(\theta^2) = \int_{0}^{1} \theta^2 \cdot \theta^{N} \cdot (1-\theta)^{M} \cdot (\frac{(N+M+1)!}{N!M!})d\theta = \frac{(N+2)!M!}{(N+M+3)!} \cdot (\frac{(N+M+1)!}{N!M!})$

$=\frac{(N+2)(N+1)}{(N+M+3)(N+M+2)}$

,a второй уже подсчитан, поэтому
$\mathbb{M_{2}} = \frac{(N+2)(N+1)}{(N+M+3)(N+M+2)} - \frac{N+1}{N+M+2}\cdot \frac{N+1}{N+M+2}$

В конечном итоге получаем:
$\mathbb{M_{2}}= \frac{ (M+1) \cdot (N+1) }{(N+M+2)^2 \cdot (N+M+3) }$
Как видно дисперсия уменьшается при добавлении данных и она симметрична относительно смены $N$ и $M$ местами.

Можно подвести итоги выкладок. При малом количестве данных надо иметь модель, параметры которой мы будем оптимизировать. Модель описывает набор предположений о реальном состоянии дел и мы выбираем наиболее подходящее предположение. Мы считаем апостериорные вероятности, если уже известны априорные. Модель должна покрывать возможные варианты, которые мы встретим на практике. При малом количестве данных модель будет выдавать большую дисперсию для выходных параметров, но по мере увеличения количества данных дисперсия будет уменьшаться и прогноз будет более однозначным.

Надо понимать, что модель, — это всего лишь модель, которая многого не учитывает. Её создает человек и вкладывает в неё ограниченные возможности. При малом количестве данных скорее сработает интуиция человека, так как человек получает намного больше сигналов из внешнего мира, и быстрее сможет сделать выводы. Такая модель скорее подойдет как элемент более сложных расчетов, так как Байес масштабируется и позволяет делать каскады из формул, которые уточняют друг друга.

На этом я бы хотел закончить свой пост. Буду рад вашим комментариям.


Ссылки

Wikipedia: Теорема Байеса
Wikipedia: Дисперсия

Комментарии (25)


  1. Ygrek
    23.01.2019 12:03
    #19649440

    В универе когда учился и подрабатывал на полставки один хороший профессор попросил сделать электронную версию ценной ему книги. Вот сейчас поискал в сети и нашел название. Книга называлась: Гаскаров, Шаповалов «Малая выборка». Показалась мне очень интересной, но в студенческие годы времени на неё не нашел.


    1. dim2r Автор
      24.01.2019 10:57
      #19655108

      Да было бы интересно заглянуть в текст.


  1. lynxrus
    23.01.2019 18:56
    #19652326

    В старых методичках СССР РТМ (руководящий технический материал) говорилось, что чтобы считать среднее и дисперсию необходимо 29 измерений. Сейчас в ВУЗах немного округлили и используют число 30 измерений.
    Колдунство какое-то которое заставляет тупо заучивать числа не понимая сути. Проблема ведь не в том что по 29 измерениям дисперсию считать нельзя, а по 30 уже можно. Проблема в статистической значимости гипотез которые можно построить по таким измерениям.
    В целом статья совсем слабая — даже для школьников. Я когда решил учить эконометрику остановился на курсе Б.Б. Демешева из НИУ ВШЭ (он есть на онлайн площадках). Вот там мат. аппарат даётся очень хорошо — вся мат. статистика по полочкам раскладывается. И программирования в R там хватает с головой.


    1. dim2r Автор
      23.01.2019 19:45
      #19652612

      У меня не было цели осветить всю мат статистику. Просто напомнил, что есть метод, который дает считать статистику с одного примера. И дает обратный ход мысли — от заданных данных к вероятности причин.


      1. Panfilov
        24.01.2019 08:44
        #19654456

        Просто напомнил, что есть метод, который дает считать статистику с одного примера.


        Извините, но нет, нет такого метода.
        Это как сказать, что вероятность встретить динозавра = 50%.


        1. dim2r Автор
          24.01.2019 09:33
          #19654664

          Если известны априорные вероятности, то можно считать апостериорные по одному случаю. В таких вопросах, как причина возникновения вселенной — неизвестны априорные. А вот в вопросах вынимания шариков — априорные известны и можно проводить оптимизацию параметров модели.


          1. Panfilov
            24.01.2019 09:58
            #19654786

            Вы пишите «Если». До этого писали «есть метод… с одного примера». Почувствуйте разницу. И теорема Байеса — это не «серебряная» пуля.
            Если мы априори знаем, что динозавры вымерли, то как построить фактическую выборку, пусть даже с одним измерением?
            Одним измерением можно более-менее опровергнуть гипотезу, но не подтвердить. Что вы вкладывает в слова «считать статистику» — для меня загадка.

            P.s. Изменено, когда заметил, что отвечаю автору.


          1. Panfilov
            24.01.2019 10:12
            #19654868

            Прошу прощения, не сразу заметил, что вы и есть автор, посыпаю голову пеплом.
            Мой посыл прост, теорема Байеса не дает нам дополнительных преимуществ или какого либо улучшения. Это просто инструмент, как молоток или отвертка. В статистике выбор модели и однородность выборки имеют куда более весомое значение. Границы применимости одного измерения или n-измерений как раз напрямую и зависят от выбранной модели.


            1. dim2r Автор
              24.01.2019 10:34
              #19654988

              Да, все зависит от того, насколько модель покрывает реальные случаи. А в случае с динозаврами, — как это узнать, покрывает ли она или нет? Нужны дополнительные данные.

              Но у Байеса есть один плюс — масштабируемость. Вы можете построить несколько моделей и связать их. Они будут уточнять друг друга из разных источников.

              В принципе модель — это модель, а не реальность. По аналогии: карта — это не местность. Нельзя сделать карту идентичную местности. Местность изменяется со временем и содержит мелкие детали. И так же нельзя сделать точную модель, на которую можно положиться во всех случаях. Можно только попытаться сделать что-то, что будет полезно для определенных случаев.


  1. Ryppka
    23.01.2019 20:13
    #19652768

    На длинах получающихся серий при смене лечения с тестируемого на контрольное и обратно, основано много адаптивных дизайнов контролируемых клинических испытаний, там, где важно сократить число испытуемых вообще и размер группы, получающей худший вариант. Деталей не помню, но этот подход был изобретен в Штатах во время второй мировой и долгое время засекречен, так как позволял сильно уменьшить расход боеприпасов при контрольных отстрелах.


  1. mas
    23.01.2019 21:54
    #19653196

    Раз уж тут статистический уголок ;) спрошу: где-то есть теория и практика измерений несколькими приборами? Я не смог найти. Т.е. не как описано выше (у нас есть N измерений постоянной величины одним и тем же прибором), а у нас есть M измерений меняющейся величины разными приборами (в отдельные моменты времени). Каждый прибор, конечно, имеет свои систематические и случайные ошибки, и поэтому кажется, что этот случай не сводится к повторным измерениям одним прибором. Интересует истинное значение измеряемой величины (хаха, ок, мат.ожидание или другая оценка) и сигма и другие характеристики. Самое простое, конечно, это среднее, но может есть что-то получше? Или, скажем, если погрешность 20 приборов 1%, и ещё пяти — 0.2%, то как подсчитать оценку величины и какова погрешность измерений 25 приборами?


    1. dim2r Автор
      23.01.2019 23:14
      #19653552

      Где-то была задачка про больного, которого проверяют на приборе и обнаруживают редкую болезнь. Прибор может иногда врать и болезнь довольно редкая. Надо было посчитать вероятность реальной болезни. Получались забавные числа, — что не надо паниковать, а надо заново проверяться. Там был расчет пр Байесу с повторной проверкой на том же приборе и на другом приборе.


  1. oracle_and_delphi
    24.01.2019 07:31
    #19654284

    Финальная картинка, где белка даёт пять — позитивчик! :)


    1. dim2r Автор
      24.01.2019 09:34
      #19654678

      она просит еще «данных» :)


  1. Panfilov
    24.01.2019 08:40
    #19654444
    +1

    Прошу прощения за критику, но статья капитанская, а формулы вставлены для научноподобности.

    Можно подвести итоги выкладок. При малом количестве данных надо иметь модель, параметры которой мы будем оптимизировать. Модель описывает набор предположений о реальном состоянии дел и мы выбираем наиболее подходящее предположение. Модель должна покрывать возможные варианты, которые мы встретим. При малом количестве данных модель будет выдавать большую дисперсию для выходных параметров, но по мере увеличения количества данных дисперсия будет уменьшаться и прогноз будет более однозначным.


    Этот пассаж, который вынесен в итог всей статьи является чуть ли не первопричиной статистики как науки.
    Основная задача статистики — проверка гипотез, в частности, на соответствие теоретической модели. Чем больше мы знаем априори об исследуемой модели, тем меньше нам нужно фактических данных, чтобы подтвердить или опровергнуть гипотезу.
    Это просто «медицинский» факт.

    Проблема широкого применения статистических методов (например в медицине) в том, что модель подгоняют под статистические измерения, которые весьма ограничены и есть проблемы с однородностью выборок, в то время как модель должна быть выбрана заранее исходя из фундаментальных предположений, и должна быть подтверждена или опровергнута с какой-то вероятностью статистическими данными.


    1. dim2r Автор
      24.01.2019 10:04
      #19654822

      А я не спорю. Нужно знать априорные, чтобы считать апостериорные. Плюс есть ход мысли от фиксированных данных к вероятности причин, а не стандартный ход от фиксированной модели к вероятным данным.


  1. dbalabanov
    24.01.2019 10:51
    #19655078

    исправьте «поразомну».


    1. dim2r Автор
      24.01.2019 11:45
      #19655380

      исправил. это словарь решил «поразмять»


  1. S_A
    24.01.2019 12:06
    #19655516
    +1

    Статья понравилась, но есть некоторые придирки. Статистика — это функция от выборки. Когда данных мало для изучения поведения статистики (интервалов например), пользуются бутстрапом. Это все "обычная" статистика.


    Байесовская действительно о большем уровне уверенности в гипотезе (или её опровержение) при получении новых свидетельств (данных). Многие называют это дело верой скорее, если так, то я верю. Потому что (спасибо за аналогию) изучая местность, мы обновляем карту.


  1. Xaliuss
    24.01.2019 12:38
    #19655732

    Если у нас есть возможность получать больше данных, то проблемы со статистиками можно решать массой способов. Но если максимальный объём выборки мал (меньше 30), то ваш метод в принципе не может улучшить статистическую значимость — среднее и дисперсия в первую очередь нужны для проверки статистических гипотез, по ним одним решения не принять.

    Поэтому в статистике при малых выборках используют критерии, не использующие среднее и дисперсию, которые завязаны на приближении нормальным распределением. Примерами могут служить ранговая корреляция, критерий Манна-Уитни, точный тест Фишера и другие.


    1. dim2r Автор
      24.01.2019 13:31
      #19656078

      Моделей много. Можно даже собрать супермодель, которая всех объединяет. Приписать каждой модели коэффициент её участия и оптимизировать эти коэффициенты точно так же, как я в статье оптимизирую theta


      1. Xaliuss
        24.01.2019 14:43
        #19656598

        Собирать супермодель это некорректный подход, при получении большого числа вторичных характеристик растёт вероятность ошибок первого рода.

        Нельзя в статистике просто брать и что-то считать. Цель исследования должна быть поставлена заранее, и выбран метод, который лучше всего подходит для задачи. Пробовать различные подходы — путь к ошибкам.


        1. dim2r Автор
          24.01.2019 14:54
          #19656672

          Не спорю, моделестроение — это тонкий процесс. Кто-то боится 5 свободных параметров включить. А кто-то и 200 миллионов включает. Например, глубокие нейронные сети содержат очень много параметров и каким-то образом выдают правильный результат несмотря на то, что эти параметры плавают.


          1. Xaliuss
            24.01.2019 15:49
            #19656998

            Так количество возможных параметров очень сильно зависит от исходных данных и их объёма. В рамках исходной задачи (малый объём выборки) предпочтительней являются модели не использующие среднее/дисперсию.


            1. dim2r Автор
              24.01.2019 16:03
              #19657072

              Большая выборка включена в априорные распределения, которые подаются на вход Байеса. Но мы можем еще и выбирать между несколькими распределениями, делая их более или менее вероятными. Достаточно получить один белый шар, чтобы заключить, что белые шары имеются в большой выборке.