
Учителя математики сотни лет мучили учеников, загоняя коз в поля странной формы. Из этой статьи вы узнаете, почему одна задачка о пасущихся козах уже более века не даёт покоя математикам. Если вы когда-нибудь сдавали экзамен по математике, то наверняка вам задавали задачку про пасущуюся козу. Её смысл заключается в следующем: рассеянный фермер оставил козу привязанной к столбу у забора или сарая, и теперь она подъедает вокруг себя всю траву, до которой может дотянуться. Ваша задача — рассчитать общую площадь, на которой может пастись коза. Давно ли вы проходили математическое тестирование?
Учителя математики сотни лет мучили учеников, загоняя коз в поля странной формы, но одна конкретная проблема с пасущимися козами не даёт покоя математикам уже более ста лет. До прошлого года им удавалось решать такие проблемы лишь приблизительно, и для получения точного решения потребовалось применение нового подхода с использованием самых современных математических методов. Давайте посмотрим, как, казалось бы, элементарная задачка, предлагаемая студентам на экзамене по математике, может превратиться в проблему, уже более века ставящую математиков в тупик.
В самом простом варианте задачи голодное животное привязывается к боковой стенке длинного сарая верёвкой фиксированной длины.
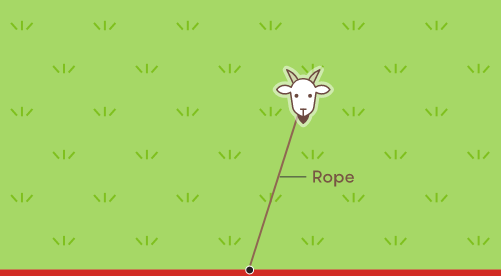
Обычно в таких задачах просят определить площадь области, в которой может перемещаться коза на верёвке. Как выглядит эта область?
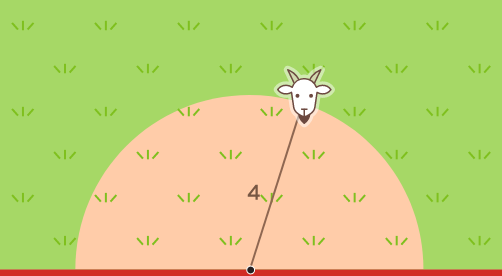
Натягивая верёвку, коза описывает полукруг и, соответственно, может дотянуться до всего, что находится внутри этого полукруга. Вот формула площади круга:
Значит, площадь полукруга в два раза меньше:
При длине верёвки 4 коза выщипает площадь (в квадратных единицах), равную
Решение этой элементарной задачи не представляет особой сложности ни для математика, ни для козы, поэтому давайте сделаем её интереснее. Что, если коза будет привязана к боковой стенке сарая квадратной формы?

Предположим, что длина верёвки и длина стороны сарая равны 4 и что верёвка прикреплена к середине одной из сторон. На какой площади теперь может пастись коза? Коза по-прежнему может пастись в том же полукруге, что и в первой задаче.

Но она также может заходить за угол сарая. Дойдя до угла, коза может использовать ещё два участка верёвки, то есть может выщипать ещё четверть круга радиусом 2 по обе стороны сарая.
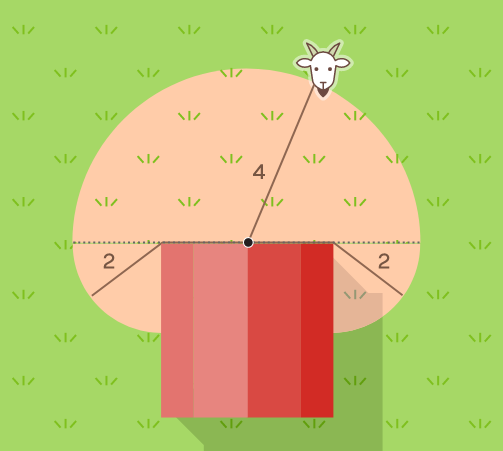
Коза может попасть в полукруг радиуса 4 плюс ещё в две четверти круга радиуса 2, общая площадь которых в квадратных единицах составляет
Задачу можно усложнить, изменив форму препятствия. Я видел задачи с козами, привязанными к треугольникам, шестиугольникам и даже к вогнутым формам.
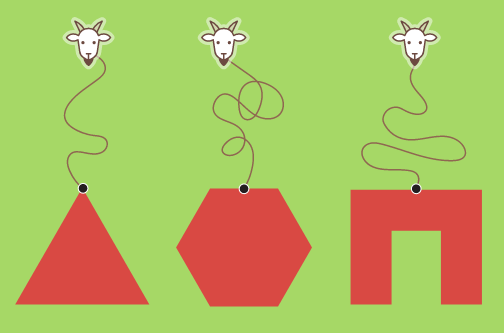
Также можно задать новое условие математической задачи, изменив её вопрос на противоположный: не указывать длину верёвки и просить найти площадь, а указать площадь и просить найти длину верёвки.
Давайте вернёмся к нашему квадратному сараю и зададим новый вопрос: какой длины должна быть верёвка, чтобы коза имела доступ к 50 квадратным единицам площади? Постановка математической задачи под новым углом может вдохнуть новую жизнь в старую идею, но при этом решение такой задачи может оказаться гораздо более сложным.
Во-первых, обратите внимание, что форма области зависит от длины верёвки. Например, если длина верёвки меньше 2 единиц, коза не сможет обогнуть угол сарая, поэтому формой области будет полукруг.
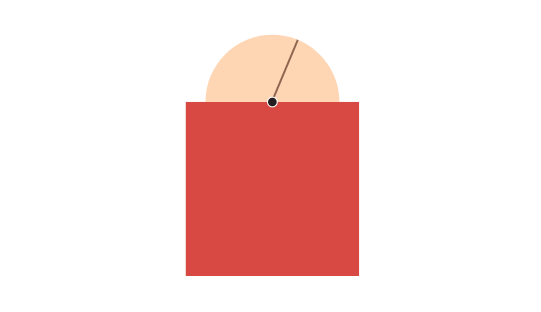
Если длина верёвки больше 2 единиц, коза сможет обогнуть угол.
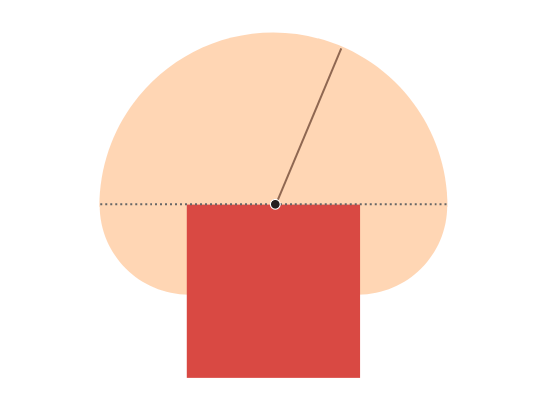
А если длина верёвки будет больше 6 единиц, коза может добраться до задней части сарая и выщипать там ещё пару четвертей круга. (Если верёвка достаточно длинная, области будут перекрываться. Соответствующий пример приведён в упражнениях в конце статьи.)
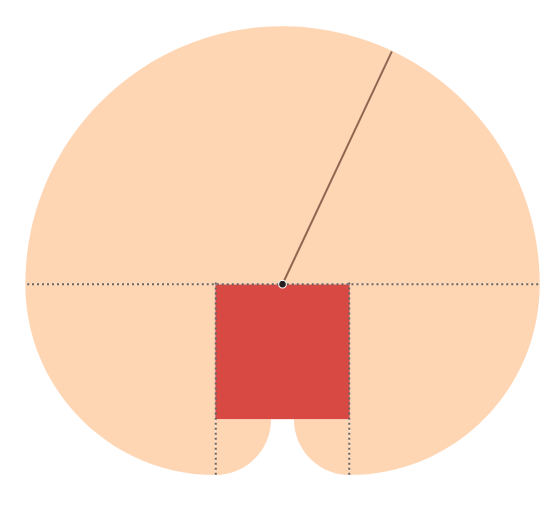
Нам необходимо найти длину верёвки, при которой общая площадь будет составлять 50 квадратных единиц. Математически это можно выполнить следующим образом: подставить в формулу площадь, равную 50, и решить это уравнение относительно r. Но для каждой области имеется своя формула расчёта площади. Какую же использовать?
Для того чтобы это выяснить, проведём небольшие вычисления. Если r ? 2, площадь области составит
Самая большая площадь будет при r = 2, то есть общая площадь составит
Это меньше 50, поэтому нам нужно более 2 единиц верёвки.
Если 2 < r ? 6, мы получаем полукруг плюс две четверти круга. Радиус полукруга равен r, а радиус четверти круга равен r – 2, так как для того, чтобы добраться до угла, потребуется две единицы верёвки, а оставшаяся верёвка выступает в качестве радиуса четверти круга с центром в углу сарая.
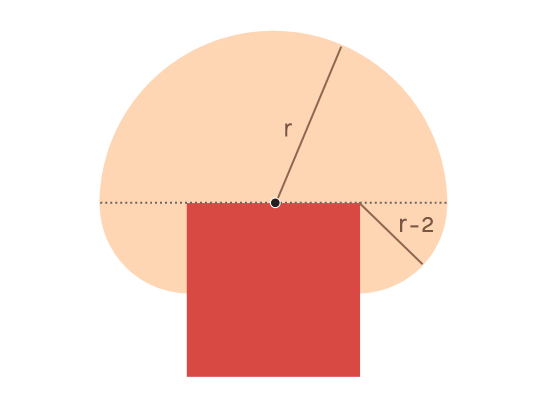
Площадь этого полукруга равна
А площадь каждой четверти круга равна
Просуммировав выражения, получим общую площадь:
Наибольшую возможную площадь мы получим при r = 6, что даёт
квадратных единиц. Поскольку 50 < 26?, это означает, что значение r, дающее 50 квадратных единиц площади, должно быть меньше 6.
Знание того, что значение r должно быть от 2 до 6 единиц, снимает вопрос о том, какую формулу для расчёта площади нужно использовать: если 2 < r ? 6, площадь
Чтобы найти точное значение r, которое даст 50 квадратных единиц площади, составим такое уравнение:
Видите, я был прав, говоря, что «перевёрнутую» задачу решать сложнее, чем оригинальную: вместо того чтобы просто вычислить площадь, которую может выщипать коза, нам нужно решить уравнение, чтобы определить длину верёвки. Для этого нужно выделить r. Чтобы перенести r в одну сторону уравнения и узнать, таким образом, его точное значение, используем арифметические и алгебраические методы.
Сначала наше уравнение может показаться немного пугающим, но по отношению к r это всего лишь квадратное уравнение. Существует стандартная процедура решения таких уравнений: представим его в форме
а затем воспользуемся формулой для решения квадратных уравнений. Немного алгебры и арифметики делают своё дело.
Возможно, это не самое красивое математическое выражение в мире, но это всего лишь квадратное уравнение, с помощью которого можно найти точное значение r. Получаем ответ:
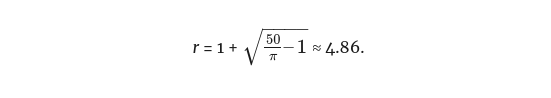
Поскольку мы смогли выделить r в уравнении, теперь мы точно знаем, какой длины должна быть верёвка, чтобы получить площадь в 50 квадратных единиц. (Обратите внимание, что найденное нами значение r, как и предполагалось, находится в пределах от 2 до 6.)
Думаете, это самая заковыристая задача с козой у сарая? Как бы не так! Математики обнаружили, что задача становится ещё более сложной, если поместить козу внутрь сарая.
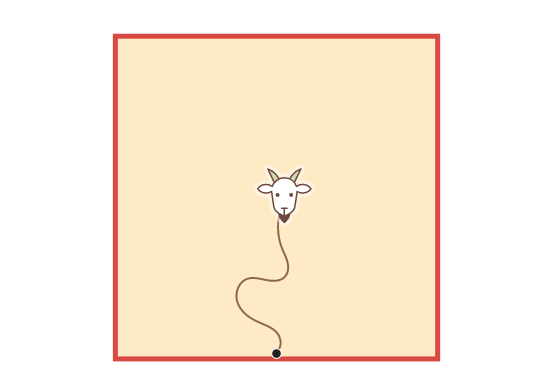
Поместим козу внутрь квадратного сарая с длиной стороны 4 и прикрепим верёвку к середине стены. Какой длины должна быть верёвка, чтобы коза могла выщипать половину площади внутри сарая?
Как было сказано выше, часть проблемы заключается в том, что форма области зависит от значения r. Чтобы получить половину площади квадрата, нужно, чтобы значение r было больше половины длины стороны сарая, но меньше полной длины стороны, что даёт нам примерно такую область.
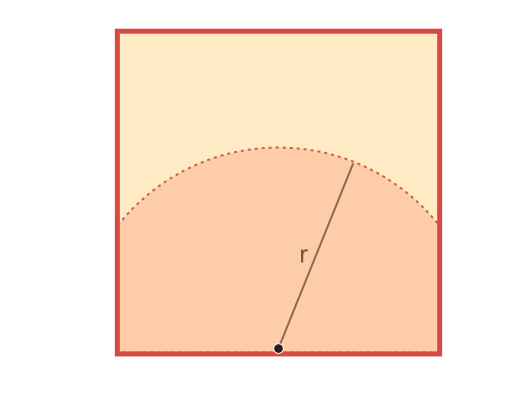
Найти формулу для такой площади не так просто. Мы можем представить область как один сектор круга радиуса r плюс два правильных треугольника, а затем для получения формулы воспользоваться геометрическими навыками из курса средней школы. Но, как мы скоро убедимся, смешение кругов и треугольников приведёт к ряду проблем.
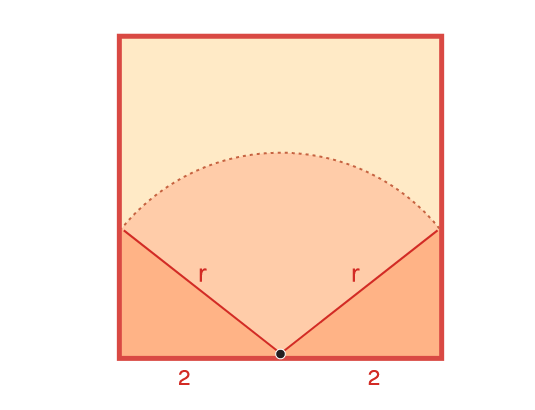
Начнём с треугольников. Согласно теореме Пифагора длины катетов в каждом правильном треугольнике равны
Таким образом, площадь одного из треугольников равна
Поэтому суммарная площадь обоих треугольников равняется
Перейдём к круговому сектору.
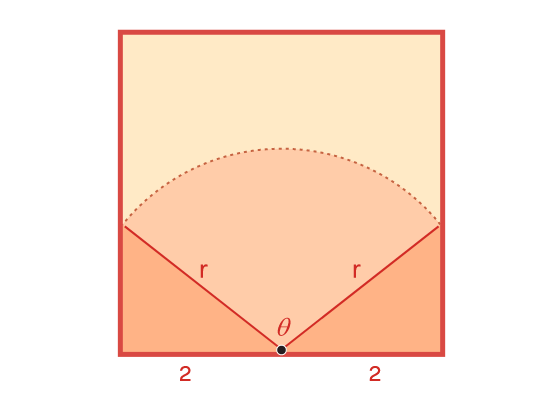
Площадь сектора равняется
где ? — значение центрального угла (в радианах, не в градусах). Нам нужна формула для расчёта площади через r, для этого необходимо выразить угол ? через r. Для этого воспользуемся теоремой косинусов — самой недооценённой теоремой из школьного курса тригонометрии.
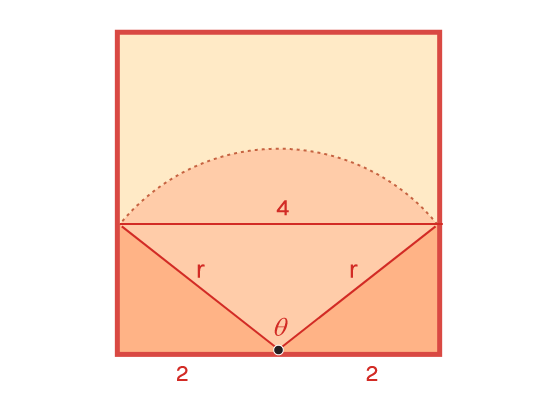
Применяя теорему косинусов к равнобедренному треугольнику со сторонами r, r и 4, получаем:
и это уравнение можно решить для cos?:
Чтобы выделить ?, нужно взять обратный косинус, или арккосинус, от обеих сторон уравнения. Это даёт:
Теперь у нас имеется угол ?, выраженный через r, поэтому площадь нашего сектора можно выразить только в r:
Окончательная формула площади — это сумма площади сектора и площадей двух треугольников, то есть:
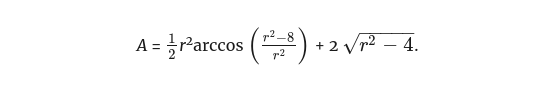
Мы получили формулу для расчёта площади области, в которой может перемещаться коза внутри квадрата, полностью через r. Теперь нужно просто найти значение r, дающее козе доступ к половине площади. Площадь всего квадрата равна 16, поэтому нам остаётся только подставить в наше уравнение A = 8, решить его относительно r, и дело сделано.
Однако возникает одна небольшая проблема: это уравнение невозможно решить относительно r.
Вернее, это уравнение невозможно решить точно относительно r. Для приблизительного определения значения r можно использовать калькулятор (получится примерно 2,331), но выделить r в нашем уравнении нельзя. Сочетание в уравнении тригонометрических и полиномиальных функций создаёт непреодолимые препятствия для его точного разрешения относительно r.
Можно попытаться вывести r из функции арккосинуса, но для этого придётся поместить другие r в функцию косинуса. В любом случае наше уравнение будет содержать трансцендентную функцию, например экспоненциальную или тригонометрическую. Трансцендентные функции нельзя выразить в терминах обычных алгебраических операций, таких как сложение и умножение, и поэтому в общем случае трансцендентные уравнения не подлежат точному решению.
Эта особенность трансцендентных функций лежит в основе известной проблемы XIX века о пасущейся козе, помещённой внутрь круглого сарая. Как и в нашей задаче с квадратным сараем, задача XIX века состояла в том, чтобы определить, какой длины должна быть верёвка, чтобы коза могла выщипать половину области.
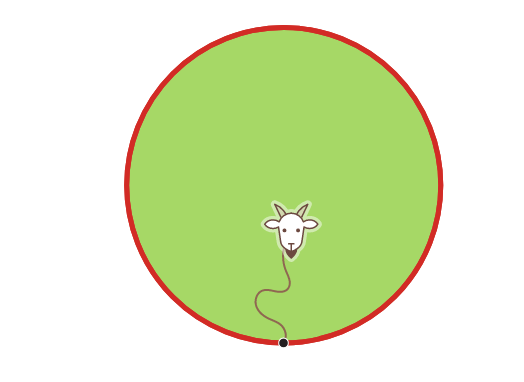
Доступная для козы область имеет форму "линзы" — два сложенных вместе круговых сегмента.
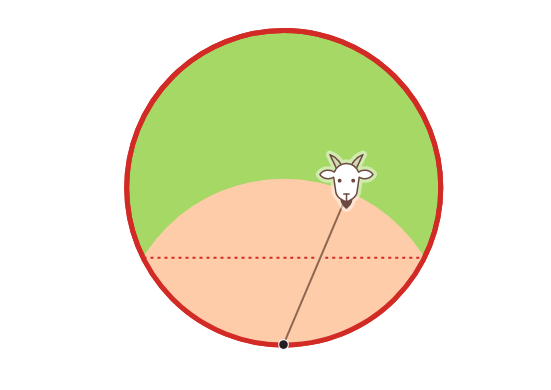
Площадь такой линзы можно, используя школьные знания по геометрии, определить по длине верёвки, однако формула получается намного сложнее, чем для квадрата. Если установить эту площадь равной половине площади круглого сарая, мы столкнемся с той же проблемой, что и при наших расчётах для козы внутри квадрата: Выделить r из уравнения не удастся. Значение r можно посчитать приближённо, но точно — никогда.
Подобное упрямство уравнения сродни упрямству козы, не находите? Более 100 лет математики пытались найти точное решение головоломки "коза в круге", но только в прошлом году немецкий математик наконец её разгадал. Для поиска точного значения r он использовал методы комплексного анализа — области математики, далёкой от геометрии кругов и квадратов, на которой основывается большинство задач о козах. И, хотя применение такого продвинутого математического инструмента, как контурный интеграл, для определения длины верёвки, к которой привязана коза, может показаться излишеством, всегда чувствуешь математическое удовлетворение после того, как делаешь то, что раньше считалось невозможным. И всегда существует вероятность, что эти новые методы, даже если они возникли в результате изучения детской задачки о козе, могут привести к открытиям, выходящим за границы деревенского сарая.
Упражнения
Если коза привязана к середине стороны квадратного сарая с длиной стороны 4 верёвкой длиной 8 единиц за пределами сарая, какова площадь области, которую может выщипать коза?
Если коза привязана к углу квадратного сарая с длиной стороны 4 верёвкой длиной 8 за пределами сарая, какова площадь области, которую может выщипать коза?
Предположим, что коза находится внутри равностороннего треугольника со стороной 4 и привязана к одной из его вершин. Какой длины должна быть верёвка, чтобы коза могла выщипать половину площади треугольника?
Если коза привязана к середине стороны квадратного сарая с длиной стороны 4 верёвкой длиной 10 за пределами сарая, какова площадь области, которую может выщипать коза?
Ответ на задачу 1
Область состоит из полукруга радиуса 8, двух четвертей окружности радиуса 6 и двух четвертей окружности радиуса 2. Поскольку 8 равно половине периметра сарая, два полукруга за сараем пересекаются в середине.
Эта площадь состоит из трёх четвертей площади окружности радиуса 8 и двух четвертей площади окружности с радиусом 4.
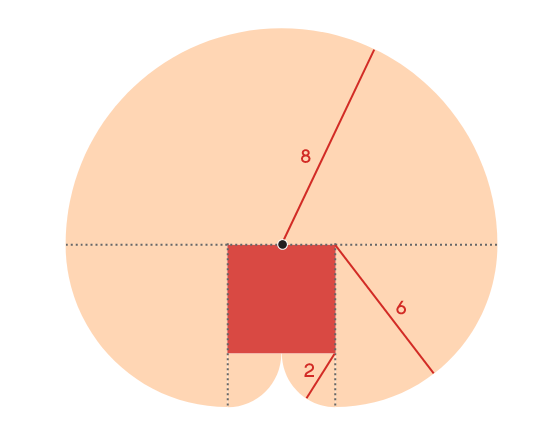
И она равна
Ответ на задачу 2
Эта область состоит из трёх четвертей окружности радиуса 8 и двух четвертей окружности радиуса 4.
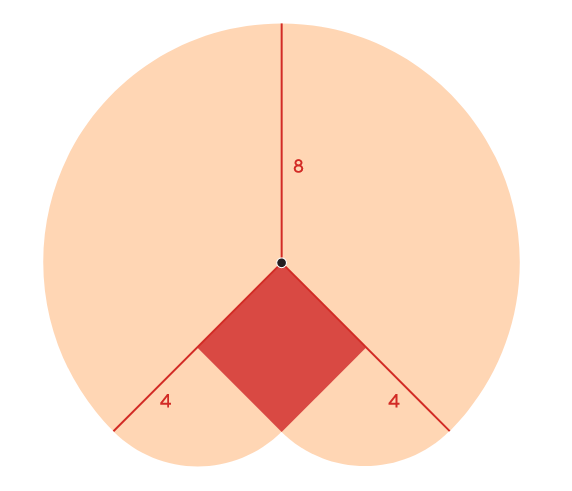
И она равна
Подумайте, что произойдёт, если длина верёвки будет равна 10.
Ответ на задачу 3
Поскольку углы равностороннего треугольника равны 60°, доступная козе площадь составляет одну шестую часть круга радиуса r, площадь которой равна
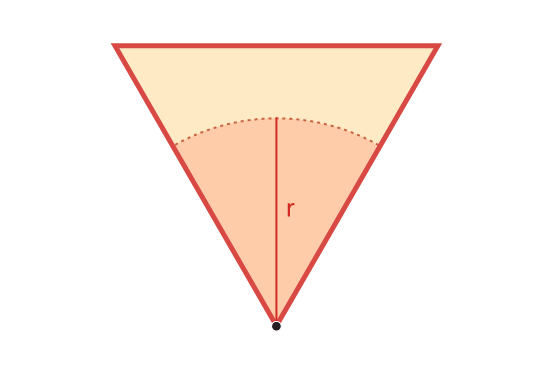
Площадь равностороннего треугольника равна
Поэтому площадь треугольника с длиной стороны 4 равна
Положим обе площади равными
И с помощью этой формулы выразим r. Мы получим
Обратите внимание, что здесь мы можем точно определить r в отличие от случая, когда в области смешаны круговые секторы и треугольники.
Ответ на задачу 4
Площадь, по-видимому, состоит из полукруга радиуса 10, двух четвертей окружности радиуса 8 и двух четвертей окружности радиуса 4. Эта площадь составляет
Но последние две четверти круга пересекаются за сараем.
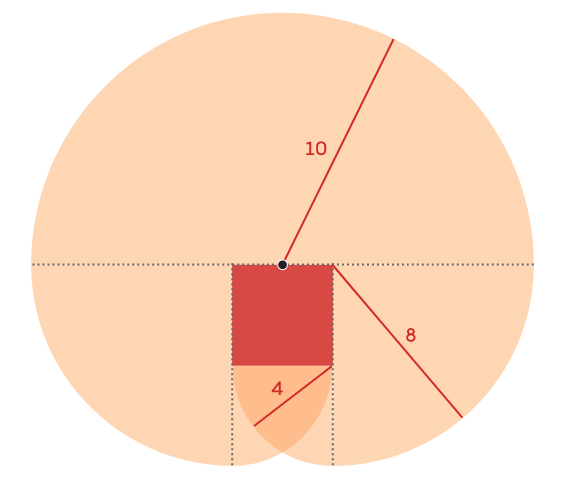
Это перекрытие было учтено дважды, поэтому нам нужно вычесть его площадь из 90?. Область перекрытия можно представить как две шестые окружности радиуса 4 минус равносторонний треугольник со стороной 4. Площадь этой области составляет
Таким образом, общая площадь равна
Примечание: это пересечение было бы гораздо сложнее найти, если бы две окружности имели разные радиусы, именно поэтому так трудно найти площадь линзы, о которой говорилось выше.
Если вам интересна не только математика, но и её практические приложения, вы можете обратить внимание на курс по Data Science: область науки о данных развивается и будет актуальна как минимум в ближайшие десять лет.

Узнайте, как прокачаться и в других специальностях или освоить их с нуля:
Другие профессии и курсы
ПРОФЕССИИ
КУРСЫ


Catslinger
Щас как озадачу!
Как привязать верёвками двух коз внутри круга, чтобы каждой досталось своя половина площади, и ничего не пропадало (не оставалось недоступным)? Можно вбить ещё колышков.
maeln0r
Привязать двух коз к колышку ровно по центру веревкой длиной r (не привязывать вообще)? Кажется, условия соблюдаются, хотя вы, конечно, имели ввиду другое.
Catslinger
Верно, двусмысленно вышло. Поправил. Спасибо.
Cost_Estimator
Catslinger
Ну мы же на плоскости. Точечные объекты. Верёвку привязывать.
Cost_Estimator
Хорошо, значит оперируем только количеством колышков. Вбиваем бесконечное их множество по диаметру круга. Коз привязываем к колышку в центре круга. Тогда каждой достанется ровно половина поля.
koldyr
Бесконечности бывают разные. Очевидно что такое счётное множество не подойдёт.
И не всякое несчетное множество подойдёт.
koldyr
Колышек ничего не даёт, так как к нему можно подойти с двух сторон.
Кончное множество колышков тоже ничего не даёт, по тем же соображениям.
allex
Вся система колышек и веревок тоже должна находиться внутри круга?
Catslinger
Нет.
allex
А веревку к другой веревке скользящей петлей можно привязывать? :)
Catslinger
Это даст красивое решение, согласен. Но можно обойтись и без.
Нужно ровно десять колышков или менее, тут два варианта. — на одну козу.
aamonster
Довольно легко доказать, что конечным количеством колышков не обойдётесь (см. выпуклость между колышками – в какую она сторону?)
Catslinger
Я обошёлся менее, чем десятью.
aamonster
Или я не понял формулировку задачи, или вы ошибаетесь.
У вас там какие-нибудь заморочки вроде петли, скользящей по верёвке, есть?
Catslinger
Никаких несертифицированных девайсов. Верёвки и точечные колышки. Уточню только, что десять или менее — на одну козу.
aamonster
Кажется, пришло время раскрывать карты. Хоть поймём, чем различается наше понимание задачи.
Catslinger
Ладно, что никто не догадался. Никто особо и не напрягался. Но никто и не загуглил, а оно же первой ссылкой выпадает. Одну верёвку, просто длинную, натягиваем по касательной к кругу. Вторую, точно равную диаметру круга, привязываем к козе обоими концами, перекинув через первую. Третью верёвку, равную радиусу круга, привязываем к козе и в центр. Готово: коза заперта в полукруг.
Альтернативно, можно вторую верёвку привязать одним концом к колышку на стороне, и опять же, перекинуть через первую. Тогда коза будет опять же ограничена прямой, находящейся под углом к первой верёвке. Но скажу честно: мне влом выводить формулу длины верёвки.
aamonster
Несколькими комментами выше я спросил:
Не поняли вопроса или специально дали такой ответ, чтобы труднее было понять правильно?
Catslinger
Ну ещё же можно вокруг первых двух кольев связать верёвку кольцом, и к ней в любом месте жёстко привязать вторую. В итоге, по верёвке нигде ничего не скользит.
aamonster
Ну да, так петля скользит по кольям. xkcd 246 :-)
Milliard
Исправьте эти две формулы. В оригинале другие.
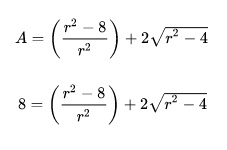
allex
Любой ученик первым делом скажет, что в сарае трава не растет! :)
Спасибо, люблю такие песочницы, где можно играясь условиями много разных задачек получить.
redf1sh
Странно, что к этой задаче не подключились физики.
Какую часть ракеты выщипает коза если она летит со скоростью 0.99с относительно наблюдателя и относительно космонавта?
Какую часть наночастиц выщипает волновой пакет нанокоз?
И тд
Sklott
А может мне кто-нибудь объяснить, почему решение имеющее в своем составе число пи считается «точным», а решение имеющее арккосинус «неточным». Ведь в любом случае при использовании числа пи мы уже получаем точность только с точностью до какого-то знака…
vesper-bot
Математически у числа пи известна вся бесконечность знаков, поэтому вычисления с использованием констант математически точные. С арккосинусом проблема в том, что точных аналитических представлений для решения уравнения вида 0=f(x)+g(trig(x)) где trig(x) — любая (ЕМНИП реально любая) тригонометрическая функция, не существует.
Lesage
Ряд маклорена, нет?
vesper-bot
Если разложить функцию в ряд Маклорена, мы получим уравнение бесконечной степени от х, а если его обрезать, можно будет получить только приближенное (численное) решение. Т.е. уравнение записать можно, а вот решение аналитически уже нельзя.
iShrimp
Как поступают математики, когда решение невозможно выразить через элементарные функции? Очень просто: придумывают специальную функцию, значение которой по определению равно требуемому.
MichaelBorisov
Среди трансцендентных уравнений попадаются и очень простые, которые не решаются.
Например, exp(a*x)+exp(b*x)=1, найти x, где a, b — параметры (произвольные действительные числа)
Для некоторых уравнений, которые не решаются, придумали специальные функции. Например, если y = x*exp(x) — то x=W(y) — функция Ламберта. С её помощью можно точно решить некоторые трансцендентные уравнения или хотя бы выразить решение в терминах специальных функций.
Аналогично y=sin(x)/x, обращения в элементарных функциях не существует.