Доброго времени суток, уважаемые хабрадамы и хабрагоспода. В этой статье мы задраим люки нашего батискафа как можно плотнее, добавим оборотов нашему питоновскому движку и погрузимся в пучины статистики, на ту глубину, в которую уже практически не проникает солнечный свет. На этой глубине мы встретим очень много самых разных статистических тестов, проплывающих мимо нас в виде причудливых формул. Сначала нам покажется, что все они устроены по-разному, но мы попробуем докопаться до самой главной движущей силы всех этих странных существ.
О чем мне следует вас предупредить перед погружением на такую глубину? Во-первых, я предполагаю, что вы уже почитали книгу Сары Бослаф "Статистика для всех", а еще покопались в официальной документации модуля stats библиотеки SciPy. Уж простите меня за мое следующее предположение, но мне кажется, что вы скорее всего были немного ошарашены огромным количеством тестов, которые там имеются, и были ошарашены еще больше, когда поняли, что это на самом деле только верхушка айсберга. Ну, а если вы еще не столкнулись со всеми прелестями этого чудесного "пубертатного периода", то рекомендую раздобыть книгу Александра Ивановича Кобзаря "Прикладная математическая статистика. Для инженеров и научных работников". Ну, а если вы "в теме", то все равно загляните под кат, почему? Потому что изложение и интерпретация фактов порой важнее и интереснее самих фактов.
Неудачный пример
Как обычно, сначала импортируем все необходимое:
import numpy as np
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt
import seaborn as sns
from pylab import rcParams
sns.set()
rcParams['figure.figsize'] = 10, 6
%config InlineBackend.figure_format = 'svg'
np.random.seed(42)А теперь представим, что есть некий руководитель отдела разработки, который решил улучшить качество работы программистов. Если честно, даже не знаю, есть ли какая-то адекватная метрика для оценки качества работы программиста, но допустим, она существует. Пусть данная метрика принимает значения из интервала [0; 10] где 0 - это "идеально", а 10 - это "жуть жутьковская". Допустим, изначально показатели выглядят вот так:
Руководитель смотрит на них и принимает следующее решение - разбить группу разработчиков на две равные части, затем отправить одну группу на курсы какой-нибудь онлайн школы, а другую группу подвергнуть добровольно-принудительному процессу самообразования. По прошествии эксперимента он снова посчитал метрики и увидел вот такие цифры:
Вот здесь надо сразу отметить, что данный пример обладает огромным количеством недостатков, и в реальности такой эксперимент просто обязан сопровождаться огромным количеством уточнений, допущений и оговорок. Планируя такие эксперименты надо сразу готовиться к тому, что обычная фриквентистская статистика тут просто недопустима. В сложных процессах мы должны уменьшать неопределенность в ходе самого процесса, по мере поступления информации о событиях внутри и снаружи этого процесса. Причем мы обязаны сохранить определенный уровень неопределенности, т.е. мы обязаны делать значительный упор на Байесовскую статистику. Могу порекомендовать книгу "Вероятностное программирование на Pуthon - Байесовский вывод и алгоритмы" Кэмерон Дэвидсон-Пайлон.
Если полностью избавиться от неопределенности, то это вызовет абсолютную уверенность, которая может привести к очень печальным последствиям. Слышали фразу "Убивает не оружие, а люди, которые используют оружие", так вот тоже самое можно сказать и про статистику - она не ошибается, ошибаются люди, которые ее используют. Можно найти немало примеров, когда незнание или неправильное понимание статистики и теории вероятностей очень сильно вредило людям: террогенные лекарства, серьезные сроки заключения под стражей, экономические кризисы и т.д. и т.п. Если интересны такие случаи, то очень рекомендую книги:
"Голая статистика" Чарльза Уилана;
"Как лгать при помощи статистики" Дарелла Хаффа;
"Парадоксы в теории вероятностей и математической статистике" Габора Секея.
Итак, попробуем представить дальнейшие действия нашего руководителя. Первым делом хочется взглянуть на данные, но поскольку их мало, то обычная гистограмма не подойдет. В этом случае лучше всего воспользоваться эмпирической функцией распределения вероятностей:
x1 = np.array([7.68,5.40,3.99,3.27,2.70,5.85,6.53,5.00,4.60,6.18])
x2 = np.array([1.33,1.66,2.76,4.56,4.75,0.70,3.13,1.96,4.60,3.69])
fig, ax = plt.subplots()
sns.ecdfplot(x=x1, ax=ax, label='До ')
sns.ecdfplot(x=x2, ax=ax, label='После')
ax.legend();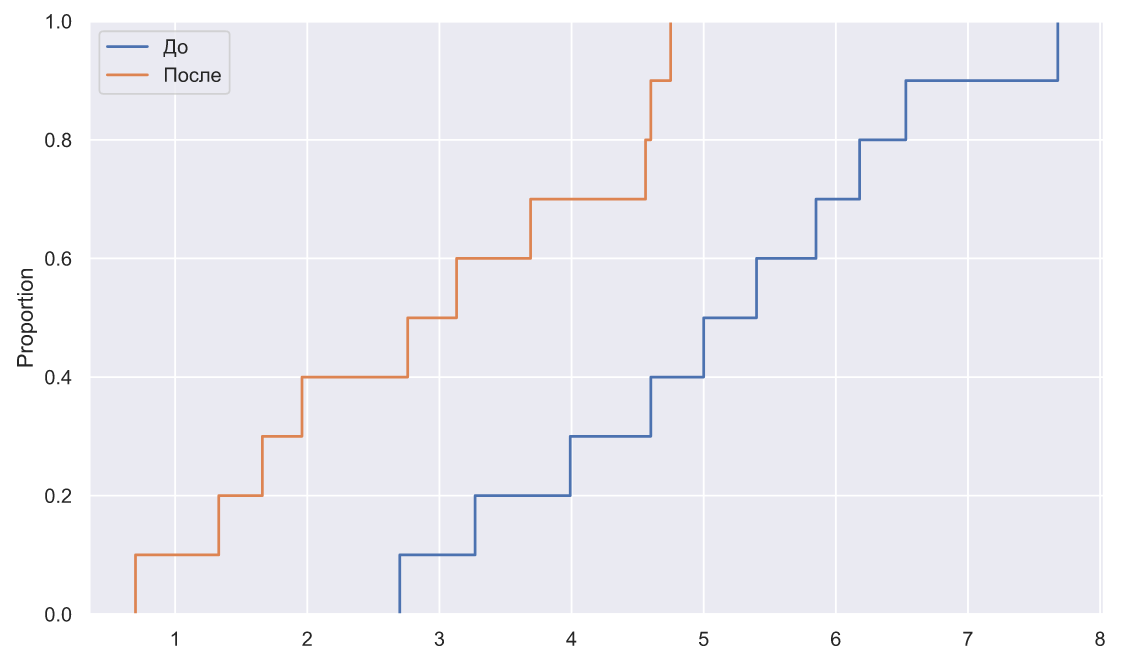
Распределение сместилось влево, хотя это вовсе не значит, что все работники показали улучшение результата (определенный индекс соответствует определенному работнику), это можно заметить по значениям метрик, или лучше нарисовать вот такой график:
plt.bar(np.arange(10), (x2-x1));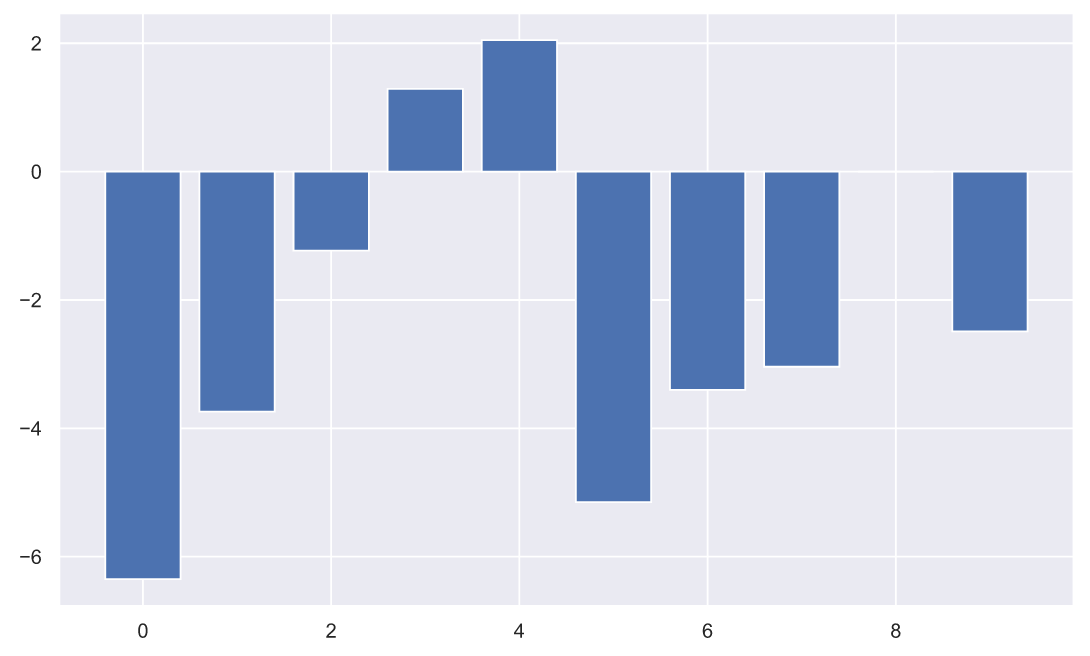
Очевидный недостаток используемой руководителем метрики заключается в том, что росту качества - соответствует уменьшение значения метрики. Наверняка, нашему руководителю придется задуматься над тем, как презентовать этот график, ведь люди могут воспринять информацию на нем абсолютно наоборот. Можно попробовать выкрутиться, просто добавив поясняющий заголовок:
plt.bar(np.arange(10), (x2-x1))
plt.xticks(np.arange(10));
plt.title('Изменение метрики качества (чем меньше - тем лучше)',
fontsize=15)
plt.xlabel('id работника', fontsize=15)
plt.ylabel('Дельта');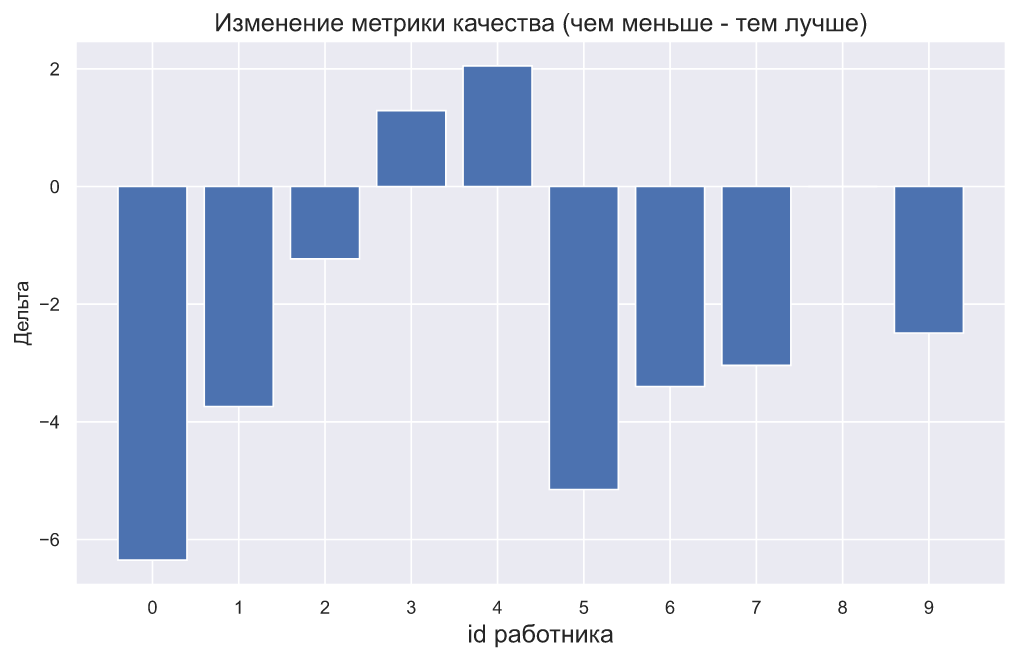
Хотя руководитель может отобразить результаты и так:
plt.bar(np.arange(10) - 0.2, x1, width=0.4, label='До')
plt.bar(np.arange(10) + 0.2, x2, width=0.4, label='После')
plt.xticks(np.arange(10))
plt.legend()
plt.title('Изменение метрики качества (чем меньше - тем лучше)',
fontsize=15)
plt.xlabel('id работника', fontsize=15)
plt.ylabel('Дельта');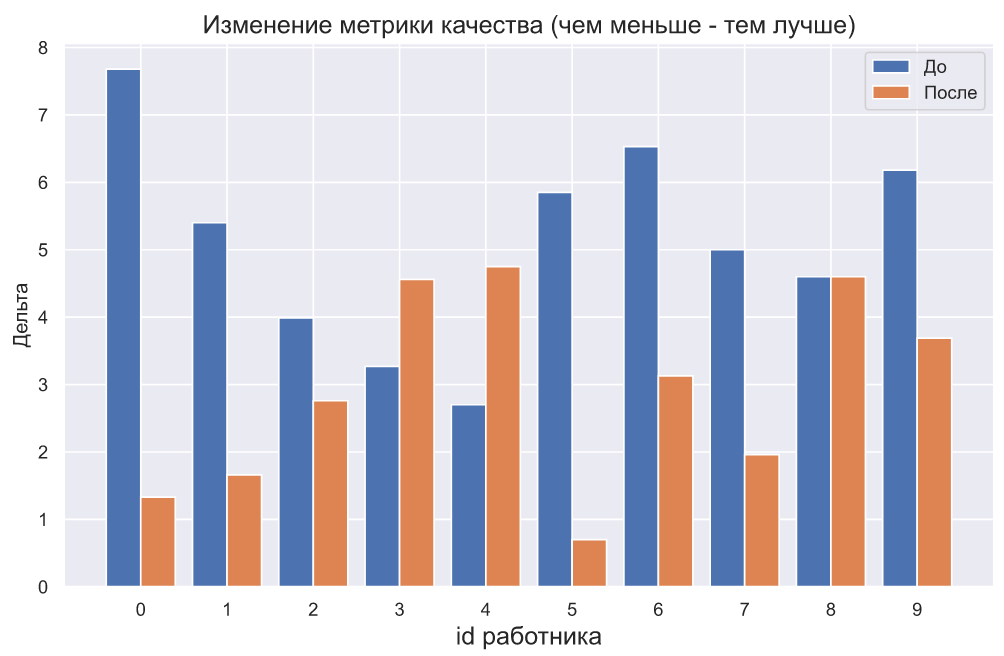
Конечно, презентация результатов с помощью графиков - это отдельная тема, и, кстати, весьма нетривиальная. Однако, давайте двинемся дальше. А дальше руководитель смотрит пристально на график, и ему с трудом верится, что подобный результат может быть получен случайно, ведь семь работников улучшили качество работы, причем некоторые из них очень значительно. Но графики и статистическая значимость - это порой очень разные вещи.
Первое, что приходит в голову - выполнить t-тест Стьюдента для зависимых выборок:
stats.ttest_rel(x2, x1)Ttest_relResult(statistic=-2.5653968678354184, pvalue=0.03041662395965993)На уровне значимости c p-value равным 0.03 можно сделать вывод о том, что результат оказался статистически значимым. В принципе, на этом можно было бы и остановиться. Но что-то не дает покоя нашему руководителю. Уместно ли применение данного теста?
У нас есть две выборки со следующими статистиками:
print(f'mean(x1) = {x1.mean():.3}')
print(f'mean(x2) = {x2.mean():.3}')
print('-'*15)
print(f'std(x1) = {x1.std(ddof=1):.3}')
print(f'std(x2) = {x2.std(ddof=1):.3}')mean(x1) = 5.12
mean(x2) = 2.91
---------------
std(x1) = 1.53
std(x2) = 1.47Чтобы выполнить t-тест мы должны предполагать, что выборки взяты из генеральных совокупностей, которые распределены хотя бы приблизительно нормально (хотя, на самом деле это не очень критично), к тому же дисперсии этих генеральных совокупностей тоже должны быть хотя бы приблизительно равны. Но с чем мы в действительности имеем дело? Стандартные отклонения выборок очень близки друг к другу, но значит ли это что и дисперсии генеральных совокупностей тоже равны? А что с требованием нормальности генеральных совокупностей? По факту нам нужно, применить центральную предельную теорему, т.е. на самом деле нам нужно, чтобы средние значения выборок имели нормальное распределение. Но как понять, работает центральная предельная теорема в нашем случае или нет?
Однородность дисперсий
Вопрос о равенстве дисперсий двух (или более) генеральных совокупностей или что то же самое - вопрос однородности дисперсий генеральных совокупностей имеет прямое отношение к так называемой проблеме Бернса-Фишера. Суть проблемы в том, что нет такого статистического теста (критерия) для сравнения средних, который был бы наиболее мощным для любых значений дисперсии генеральных совокупностей. А это означает, что мы всегда должны выдвигать какие-то предположения о дисперсиях совокупностей. Самое простое - предположить, что дисперсии генеральных совокупностей равны. Чуть сложнее предположить, что дисперсии генеральных совокупностей имеют различные, но все-таки какие-то конкретные значения. Но мы не можем придумать какой-то критерий, который учитывал бы абсолютно все значения дисперсий.
Смотрите, наш руководитель применил t-тест для зависимых выборок, рассчитывая на то, что мат.ожидание генеральной совокупности сместилось влево, но при этом никакого изменения дисперсии не произошло. Тем более выборочные стандартные отклонения практически равны, что придает еще большей уверенности. Но что, если это всего лишь случайное совпадение?
Для начала мы можем посмотреть на то, как будут распределены выборочные дисперсии двух генеральных совокупностей. Для этого сгенерируем по 5000 выборок из распределений и
по 10 элементов в каждой выборке, затем вычислим выборочную дисперсию для каждой из них:
samples = stats.norm.rvs(loc=(5, 3), scale=1.5, size=(5000, 10, 2))
deviations = samples.var(axis=1, ddof=1)
deviations_df = pd.DataFrame(deviations, columns=['s1', 's2'])
sns.histplot(data=deviations_df, element="poly", color='r', fill=False);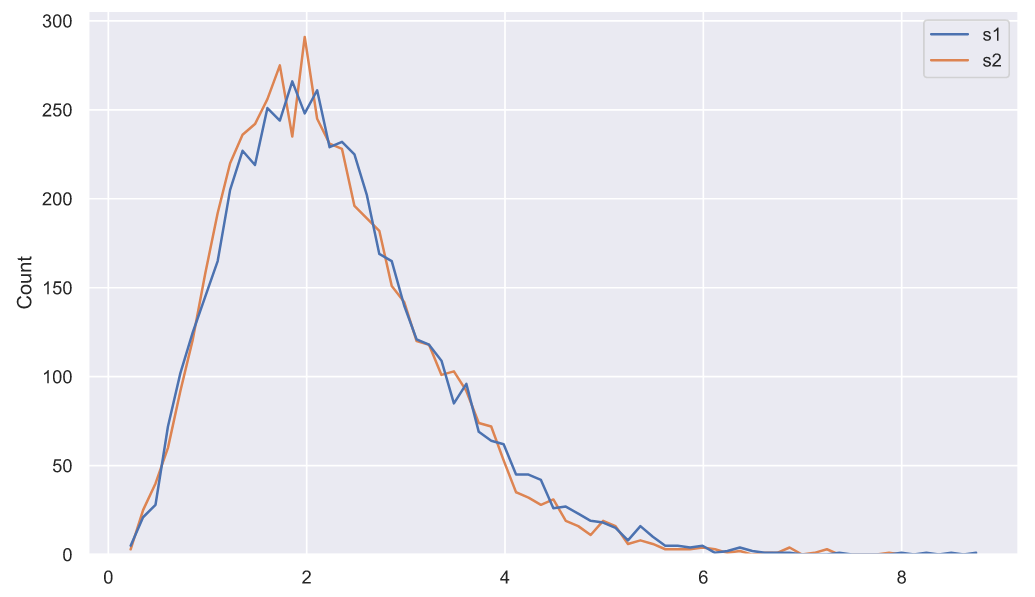
врезка по поводу качества кода
Иногда бывает так, что абсолютно никому нет дела до вашего кода, от слова "совсем" - главное результат. Поэтому появляется соблазн генерировать вот такую лапшу:
sns.histplot(data=pd.DataFrame(np.std(stats.norm.rvs(loc=(5, 3), scale=1.5, size=(5000,10,2)), axis=1, ddof=1), columns=['s1', 's2']), element="poly", color='r', fill=False);Если это "одноразовый" код - то пожалуйста. Но если есть хоть какая-то вероятность того, что к этому коду придется вернуться, то лучше оформлять код в более понятном виде:
простое - разделяется на шаги;
сложное разделяется на шаги и снабжается комментариями;
запутанное разбивается на шаги, снабжается комментариями и пояснениями.
Бывает и так, что ваш код должен быть чем-то вроде "полуфабриката", который будет переписываться на другие языки и затачиваться под разные "хотелки". В этом случае лучше отказаться от всякого "синтаксического сахара", т.е. кодить максимально просто. Скорее всего, человек, который будет переписывать ваш код по дефолту, будет обладать неприлично большим уровнем компетентности в вопросах разработки. Но этот простой совет может очень сильно упростить жизнь как вам, так и этому человеку.
Чтобы облегчить сравнение двух распределений можно изображать их в виде полигонов, как мы и поступили. На этом графике мы видим, что дисперсии распределены одинаково, что неудивительно, так как отклонения генеральных совокупностей равны. Еще можно наблюдать некоторую асимметрию: левый "хвост" короче правого. Думаю, что уже нет никакого смысла ходить "вокруг, да около" и вы уже давным-давно поняли, что речь пойдет о хи-квадрат распределении. Оценить параметры распределения можно с помощью метода максимального правдоподобия, который реализован в методе fit():
df1, loc1, scale1 = stats.chi2.fit(deviations_df['s1'], fdf=10)
print(f'df1 = {df1}, loc1 = {loc1:<8.4}, scale1 = {scale1:.3}')
df2, loc2, scale2 = stats.chi2.fit(deviations_df['s2'], fdf=10)
print(f'df2 = {df2}, loc2 = {loc2:<8.4}, scale1 = {scale2:.3}')df1 = 10, loc1 = -0.1027 , scale1 = 0.238
df2 = 10, loc2 = -0.08352, scale1 = 0.231fig, ax = plt.subplots()
# гистограммы придется рисовать по отдельности, иначе
# площадь под каждой из них будет равна 0.5 а не 1:
sns.histplot(data=deviations_df['s1'], color='r', element='poly',
fill=False, stat='density', label='s1', ax=ax)
sns.histplot(data=deviations_df['s2'], color='b', element='poly',
fill=False, stat='density', label='s2', ax=ax)
chi2_rv1 = stats.chi2(df1, loc1, scale1)
chi2_rv2 = stats.chi2(df2, loc2, scale2)
x = np.linspace(0, 8, 300)
sns.lineplot(x=x, y=chi2_rv1.pdf(x), color='r', label='pdf(s1)', ax=ax)
sns.lineplot(x=x, y=chi2_rv2.pdf(x), color='b', label='pdf(s2)', ax=ax)
ax.set_xticks(np.arange(10))
ax.set_xlabel('s');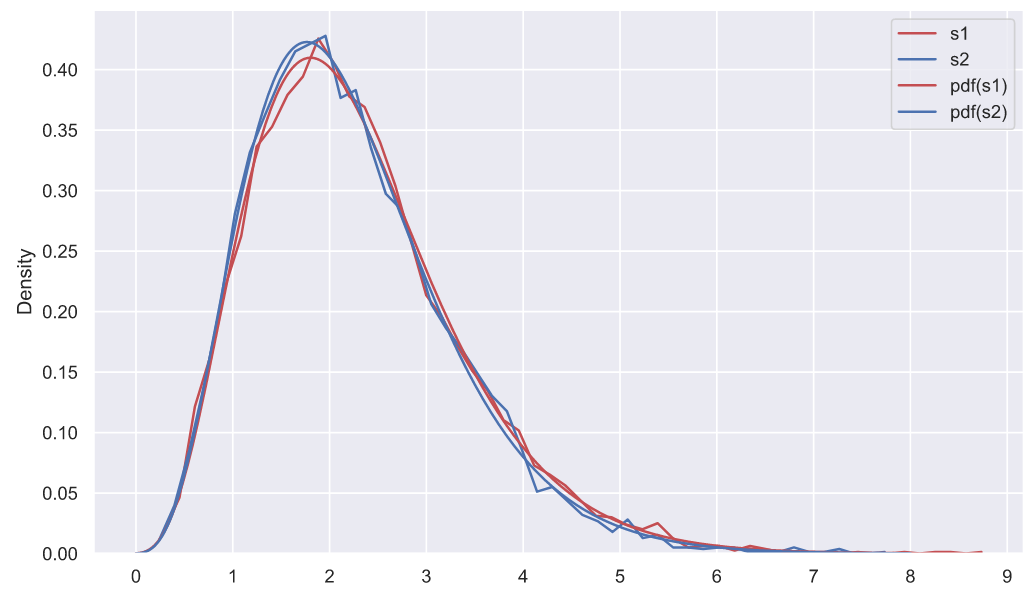
Что означают параметры смещения и масштаба для какого-то определенного распределения всегда можно уточнить в документации. Эти параметры не всегда просто интерпретировать, но иногда их использование гораздо удобнее, чем переход к стандартизированным случайным переменным, хотя бы просто потому, что это облегчает восприятие информации на графиках, так как на них видно именно те значения, которые характерны для неизмененных данных (наших выборок). Еще не мешало бы сказать пару слов о методе максимального правдоподобия и обязательно упомянуть о методе моментов. Если вы хотите понять, как линейная алгебра ("линейка"), математический анализ ("матан") и вычислительная математика ("вычмуты") связаны с математической статистикой ("статами"), то лучше ознакомиться с этими методами, а еще лучше разобраться с тем, как они работают. Хотя, если вы покопаетесь в журналах , то с удивлением обнаружите, что "щупальца" математической статистики проскользнули практически во все разделы математики, что как минимум, занимательно.
Мы построили график и что дальше? У нас есть функции распределения плотности вероятности для выборочных дисперсий, взятых из двух генеральных совокупностей, распределенных как и
. Причем мы видим, что эти функции практически идентичны. Как мы можем использовать эти функции? Допустим, мы извлекли выборку из десяти элементов стандартное отклонение которой равно 2, может ли выборка с таким отклонением быть получена случайно из генеральной совокупности с распределением
?
fig, ax = plt.subplots()
var = 2**2
x = np.linspace(0, 10, 300)
sns.lineplot(x=x, y=chi2_rv1.pdf(x), label='pdf(s1)', ax=ax)
ax.vlines(var, 0, chi2_rv1.pdf(var), color='r', lw=2)
ax.fill_between(x[x>var], chi2_rv1.pdf(x[x>var]),
np.zeros(len(x[x>var])), alpha=0.3, color='b')
ax.hlines(0, x.min(), x.max(), lw=1, color='k')
p = chi2_rv1.sf(var)
ax.set_title(f'$P(s_{1} \geqslant {var}) = $' + '{:.3}'.format(p))
ax.set_xlabel('s');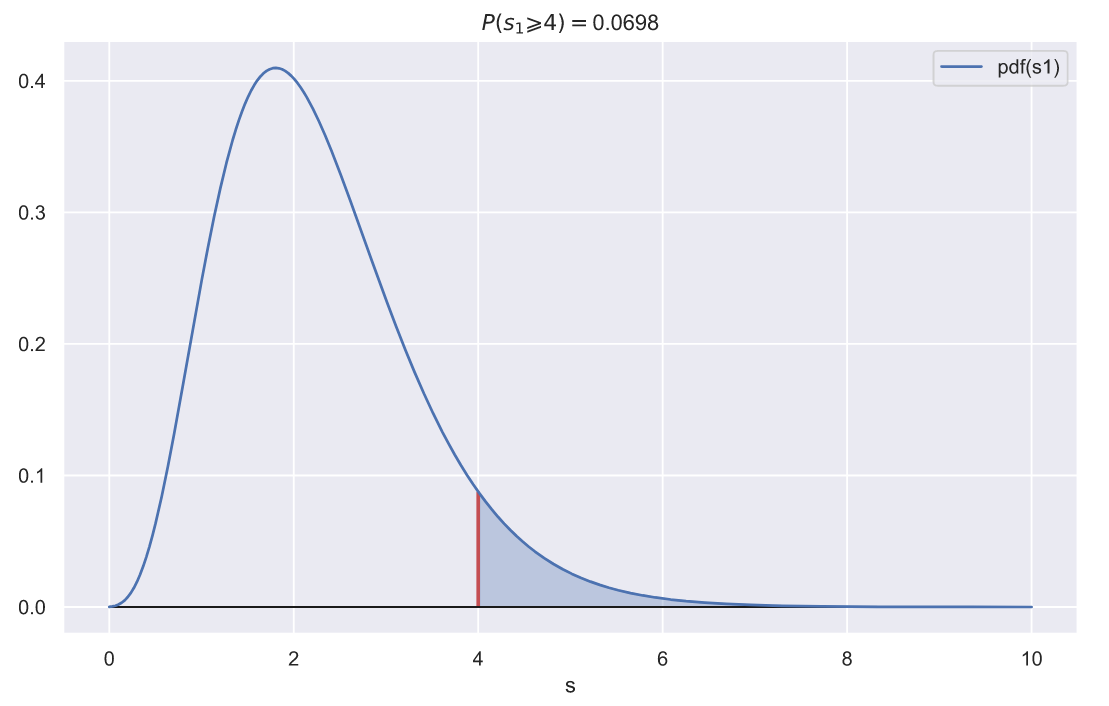
Полученное p-value не так уж и велико, а это значит, что получить выборку, состоящую из 10 элементов из генеральной совокупности с распределением и выборочным стандартным отклонением
не так то уж и просто. Впору засомневаться в том, что отклонение генеральной совокупности
действительно равно 1.5. Однако, если уровень значимости задан как
, то мы все-таки должны признать, что получение выборки с таким отклонением обусловлено случайностью.
С другой стороны, мы всегда можем задать какую-то область, вероятность попадания в которую будет равна заданному значению, например 0.1:
fig, ax = plt.subplots()
x = np.linspace(0, 10, 300)
sns.lineplot(x=x, y=chi2_rv1.pdf(x), label='pdf(s1)', ax=ax)
# определяем критические значения:
ci_left, ci_right = chi2_rv1.interval(0.9)
ax.vlines([ci_left, ci_right], 0, 0.5, color='r', lw=2)
x_le_ci_l, x_ge_ci_r = x[x<ci_left], x[x>ci_right]
ax.fill_between(x_le_ci_l, chi2_rv1.pdf(x_le_ci_l),
np.zeros(len(x_le_ci_l)), alpha=0.3, color='b')
ax.fill_between(x_ge_ci_r, chi2_rv1.pdf(x_ge_ci_r),
np.zeros(len(x_ge_ci_r)), alpha=0.3, color='b')
ax.set_title(f'P({ci_left:.3} $\geqslant s_{1} \geqslant$ {ci_right:.3}) = 0.1')
ax.hlines(0, x.min(), x.max(), lw=1, color='k')
ax.set_xlabel('s');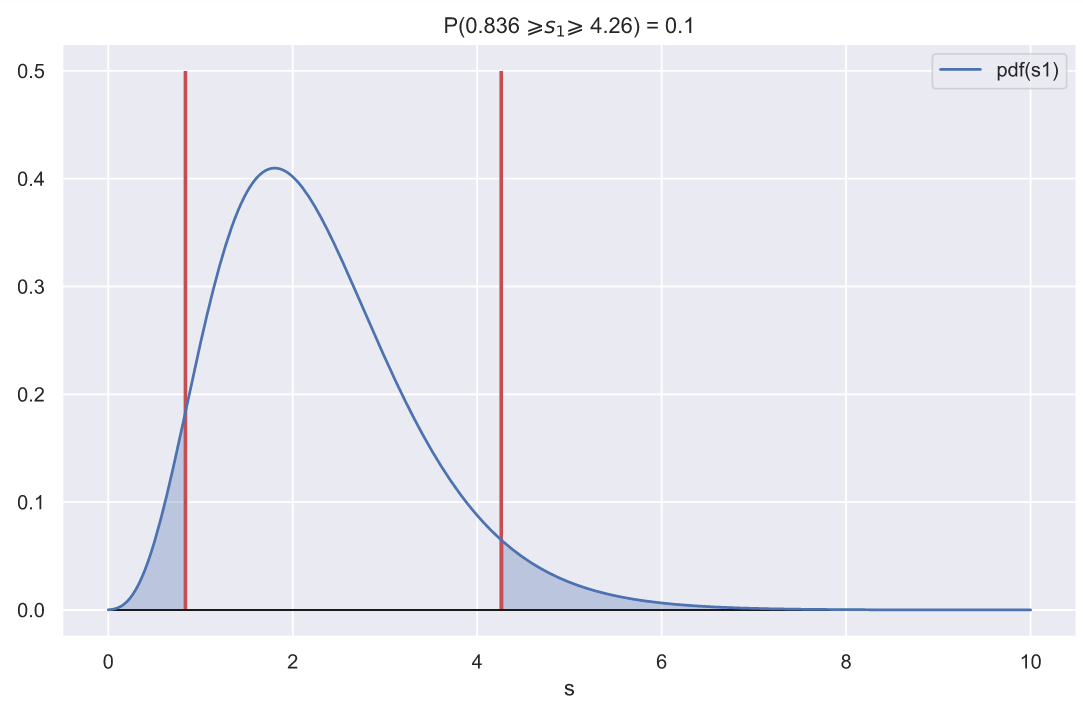
Если отклонение от вершины распределения превысит указанный диапазон, то с мы можем утверждать, что данное отклонение обусловлено какими-то факторами, повлиявшими на генеральную совокупность, но не случайностью.
А что насчет равенства дисперсий двух генеральных совокупностей? Очевидно, отношение выборочных дисперсий тоже должно быть как-то распределено. Давайте взглянем, как распределена величина:
где это номер выборки:
rel_dev = deviations_df['s1'] / deviations_df['s2']
sns.histplot(x=rel_dev, stat='density');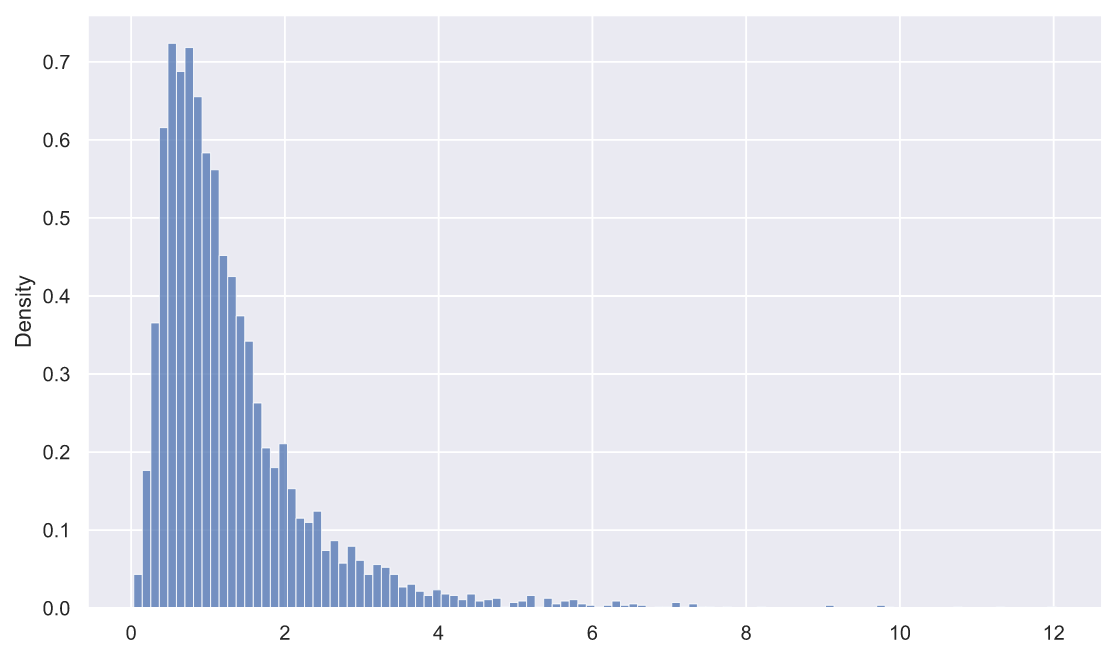
Перед нами распределение Фишера, узнать параметры которого можно с помощью все того же метода fit():
dfn, dfd, loc, scale = stats.f.fit(rel_dev, fdfn=10, fdfd=10)
print(f'dfn = {dfn}, dfd = {dfd}, loc2 = {loc2:<8.4}, scale1 = {scale2:.3}')dfn = 10, dfd = 10, loc2 = -0.08352, scale1 = 0.231fig, ax = plt.subplots()
rel_dev = deviations_df['s1'] / deviations_df['s2']
sns.histplot(x=rel_dev, stat='density', alpha=0.4)
f_rv = stats.f(dfn, dfd, loc, scale)
x = np.linspace(0, 12, 300)
ax.plot(x, f_rv.pdf(x), color='r')
ax.set_xlim(0, 8);
Функция распределения плотности вероятности на этом графике позволяет проверять гипотезы о равенстве дисперсий генеральных совокупностей. Например, если из первой генеральной совокупности была извлечена выборка с дисперсией равной 3, а из второй совокупности выборка с дисперсией равной 1, то получить случайным образом две такие выборки будет крайне трудно:
fig, ax = plt.subplots()
rel_var = 3
x = np.linspace(0, 8, 300)
sns.lineplot(x=x, y=f_rv.pdf(x), label='pdf(s1)', ax=ax)
ax.vlines(rel_var, 0, f_rv.pdf(rel_var), color='r', lw=2)
ax.fill_between(x[x>rel_var], f_rv.pdf(x[x>rel_var]),
np.zeros(len(x[x>rel_var])), alpha=0.3, color='b')
ax.hlines(0, x.min(), x.max(), lw=1, color='k')
p = f_rv.sf(var)
ax.set_title(f'$P(s_{1}/s_{2} \geqslant {rel_var}) = $' + '{:.3}'.format(p))
ax.set_xlabel('s');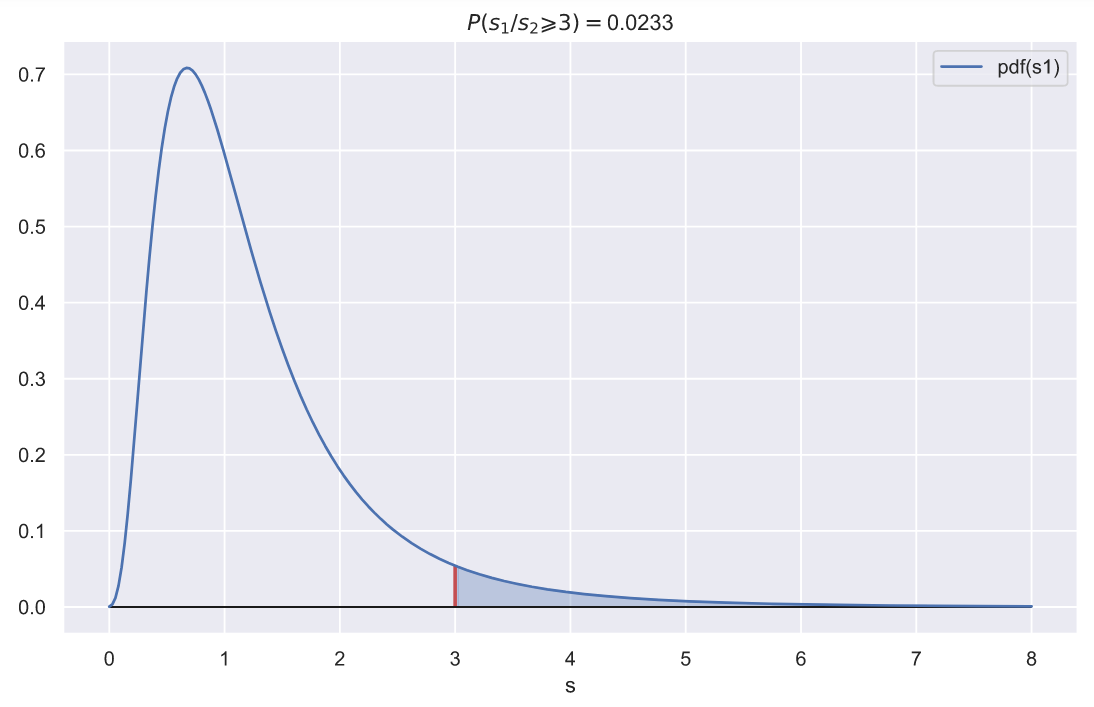
То есть, если мы будем попарно извлекать две выборки по 10 элементов в каждой из двух генеральных совокупностей с распределениями и
, то вероятность того, что отношение дисперсий этих выборок окажется равным или большим 3, составит всего 0.023. А это хороший повод засомневаться в том, что дисперсии генеральных совокупностей равны.
Отношение выборочных дисперсий в нашем примере равно:
np.var(x1, ddof=1) / np.var(x2, ddof=1)1.083553459313125Так что наш руководитель может быть спокоен по поводу равенства дисперсий двух генеральных совокупностей. Однако ему вдруг становится очень любопытно, почему для сравнения средних, приходится так много возиться с дисперсиями. Может быть, попробовать дисперсионный анализ? ANOVA? Просто предположим, что мы имеем дело с двумя независимыми выборками, как будто бы у нас на самом деле две группы программистов, одна из которых участвовала в образовательном процессе, а другая нет. Давайте воспользуемся функцией f_oneway() и посмотрим на результат (чем меньше значение pvalue, тем меньше вероятность того, что средние генеральных совокупностей равны):
stats.f_oneway(x1, x2)F_onewayResult(statistic=10.786061383971454, pvalue=0.0041224402038065235)Но что скрывается под капотом этого теста? Может что-то жутко сложное и непонятное?
Однофакторный дисперсионный анализ
На самом деле принцип работы выполненного выше теста чрезвычайно прост, и мы можем легко воспроизвести работу функции f_oneway(), для чего нам понадобятся всего две формулы:
m1, m2, m = *np.mean((x1, x2), axis=1), np.mean((x1, x2))
ms_bg = (10*(m1 - m)**2 + 10*(m2 - m)**2)/(2 - 1)
ms_wg = (np.sum((x1 - m1)**2) + np.sum((x2 - m2)**2))/(20 - 2)
s = ms_bg/ms_wg
p = stats.f.sf(s, dfn=1, dfd=18)
print(f'statistic = {s:.5}, p-value = {p:.5}')statistic = 10.786, p-value = 0.0041224 (mean square between group) просто показывает, как среднее каждой группы отклоняется от общего среднего. Очевидно, что чем меньше средние групп отличаются друг от друга, тем меньше значение
. С другой стороны
(mean square within group) показывает, что если средние групп не слишком сильно отличаются друг от друга, то внутригрупповая дисперсия практически не будет отличаться от общегрупповой. Эти две формулы нужны для того, чтобы статистически обосновать различие средних групп, но они являются ничем иным, как формулами для вычисления дисперсии. Согласитесь, в этом есть какой-то парадокс, ведь сравнивая средние, мы по сути сравниваем дисперсии. В поддержку утверждения того, что это действительно дисперсии говорит и тот факт, что отношение
к
имеет распределение Фишера:
В чем довольно легко убедиться:
N = 10000
samples_1 = stats.norm.rvs(loc=0, scale=1, size=(N, 10))
samples_2 = stats.norm.rvs(loc=0, scale=1, size=(N, 10))
m1 = samples_1.mean(axis=1)
m2 = samples_2.mean(axis=1)
m = np.hstack((samples_1, samples_2)).mean(axis=1)
ms_bg = 10*((m1 - m)**2 + (m2 - m)**2)
ss_1 = np.sum((samples_1 - m1.reshape(N, 1))**2, axis=1)
ss_2 = np.sum((samples_2 - m2.reshape(N, 1))**2, axis=1)
ms_wg = (ss_1 + ss_2)/18
statistics = ms_bg/ms_wg
f, ax = plt.subplots()
x = np.linspace(0.02, 30, 500)
plt.plot(x, stats.f.pdf(x, dfn=1, dfd=18), color='r', label=f'f.pdf(x, 1, 18, 0, 1)')
plt.legend()
sns.histplot(x=statistics, binwidth=0.1, stat='density', alpha=0.5)
ax.set_xlim(0, 6)
ax.set_title(r'Распределение $MS_{bg} \; / \;MS_{wg}$ стандартизированных случайных значений');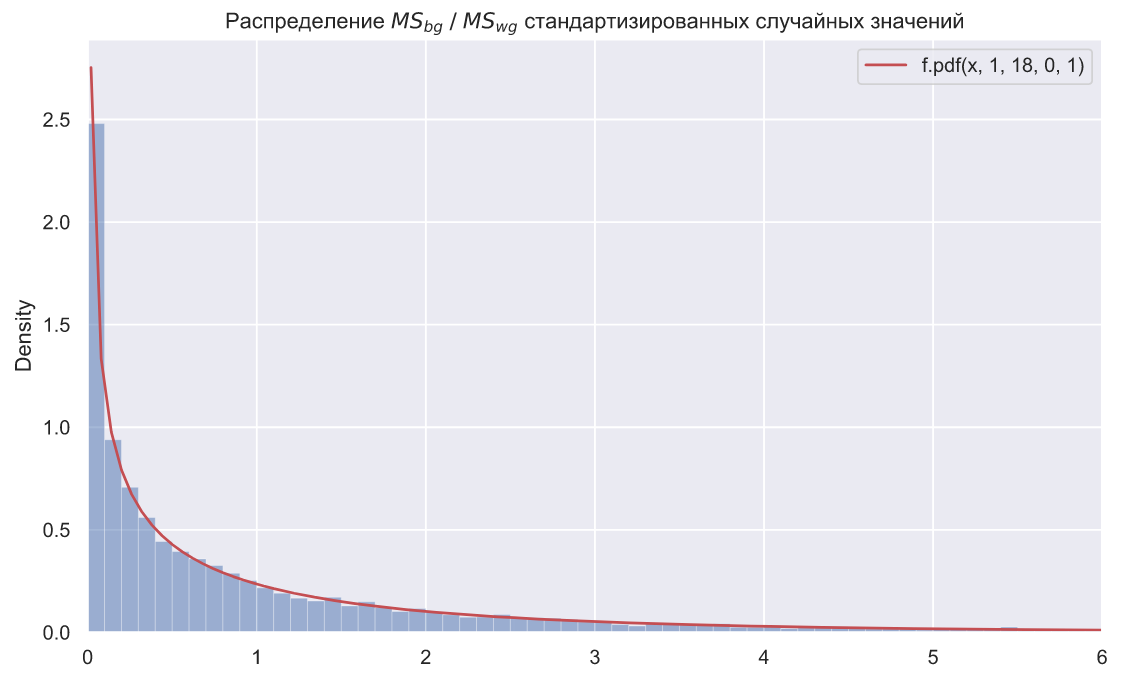
Код для картинки
N = 10000
mu_1 = stats.uniform.rvs(loc=0, scale=5, size=(N, 1))
samples_1 = stats.norm.rvs(loc=mu_1, scale=2, size=(N, 10))
mu_2 = stats.uniform.rvs(loc=0, scale=5, size=(N, 1))
samples_2 = stats.norm.rvs(loc=mu_2, scale=2, size=(N, 10))
m1 = samples_1.mean(axis=1)
m2 = samples_2.mean(axis=1)
m = np.hstack((samples_1, samples_2)).mean(axis=1)
ms_bg = 10*((m1 - m)**2 + (m2 - m)**2)
ss_1 = np.sum((samples_1 - m1.reshape(N, 1))**2, axis=1)
ss_2 = np.sum((samples_2 - m2.reshape(N, 1))**2, axis=1)
ms_wg = (ss_1 + ss_2)/18
statistics = ms_bg/ms_wg
loc, scale = stats.f.fit(statistics, fdfn=1, fdfd=18)[-2:]
f, ax = plt.subplots()
x = np.linspace(0.02, 30, 500)
plt.plot(x, stats.f.pdf(x, dfn=1, dfd=18, loc=loc, scale=scale), color='r', label=f'f.pdf(x, 1, 18, {loc:.3}, {scale:.3})')
plt.legend()
sns.histplot(x=statistics, binwidth=0.2, stat='density', alpha=0.5)
ax.set_xlim(0, 20)
ax.set_title(r'Распределение $MS_{bg} \; / \;MS_{wg}$ нестандартизированных случайных значений');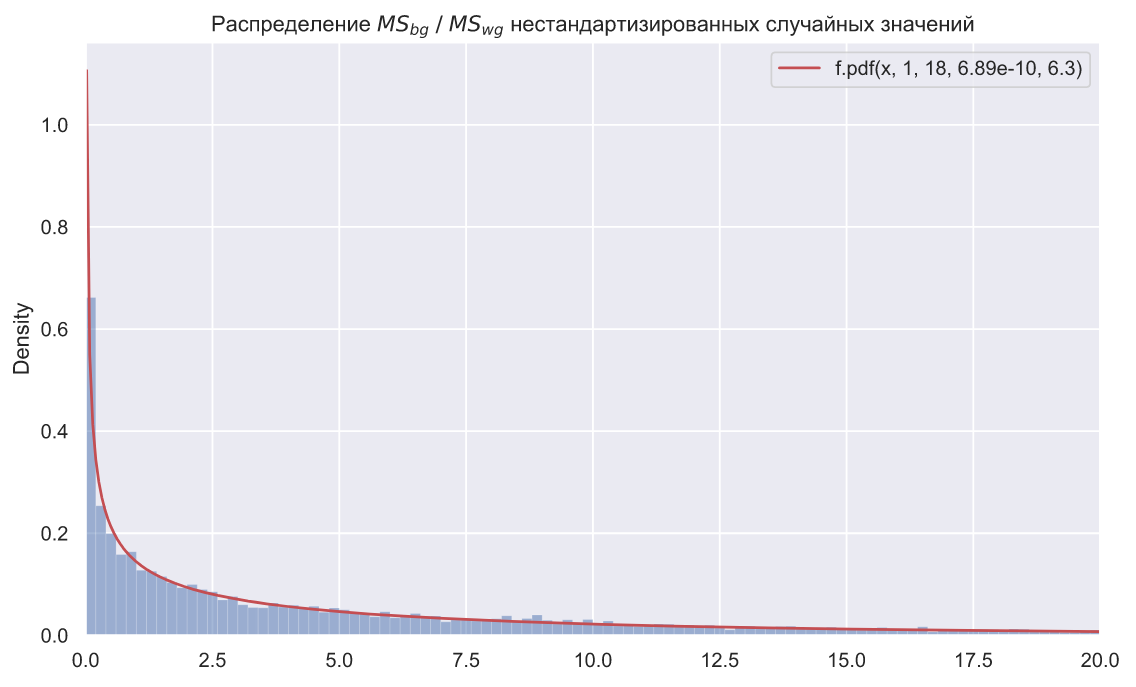
Вы можете попробовать воспроизвсти работу теста Левене, который реализован в SciPy как функция levene(). Этот тест (критерий) устроен точно так же, как однофакторный ANOVA, но проверяет гипотезу о равенстве дисперсий генеральных совокупностей:
stats.levene(x1, x2)LeveneResult(statistic=0.0047521397921121405, pvalue=0.9458007897725039)Гипотеза о "нормальности"
Суть центральной предельной теоремы заключается в том, что чем больше объем выборки, тем сильнее выборочное среднее будет стремиться к нормальному распределению. Благодаря данной теореме, мы, например, можем пользоваться критерием Стьюдента, даже если знаем, что генеральная совокупность имеет распределение отличное от нормального. Но беда в том, что центральная предельная теорема работает только для выборочного среднего, но не для выборочной дисперсии. Это очень легко продемонстрировать на следующем примере: сгенерируем 10000 выборок по 5 элементов в каждой из стандартных нормального, равномерного и лапласова распределений, а затем сравним, как будут распределены суммы квадратов элементов каждой выборки:
N, k = 10000, 5
func = [stats.uniform, stats.norm, stats.laplace]
color = list('gyb')
labels = ['s_uniform', 's_norm', 's_laplace']
for i in range(3):
ss = np.square(func[i].rvs(size=(N, k))).sum(axis=1)
sns.histplot(x=ss, stat='density', label=labels[i] + '.pdf(x)',
element='step', color=color[i], lw=2, fill=False)
x = np.linspace(0, 25, 300)
plt.plot(x, stats.chi2.pdf(x, df=5), color='r', label='chi2.pdf(x, df=5)')
plt.legend()
plt.xlim(0, 20);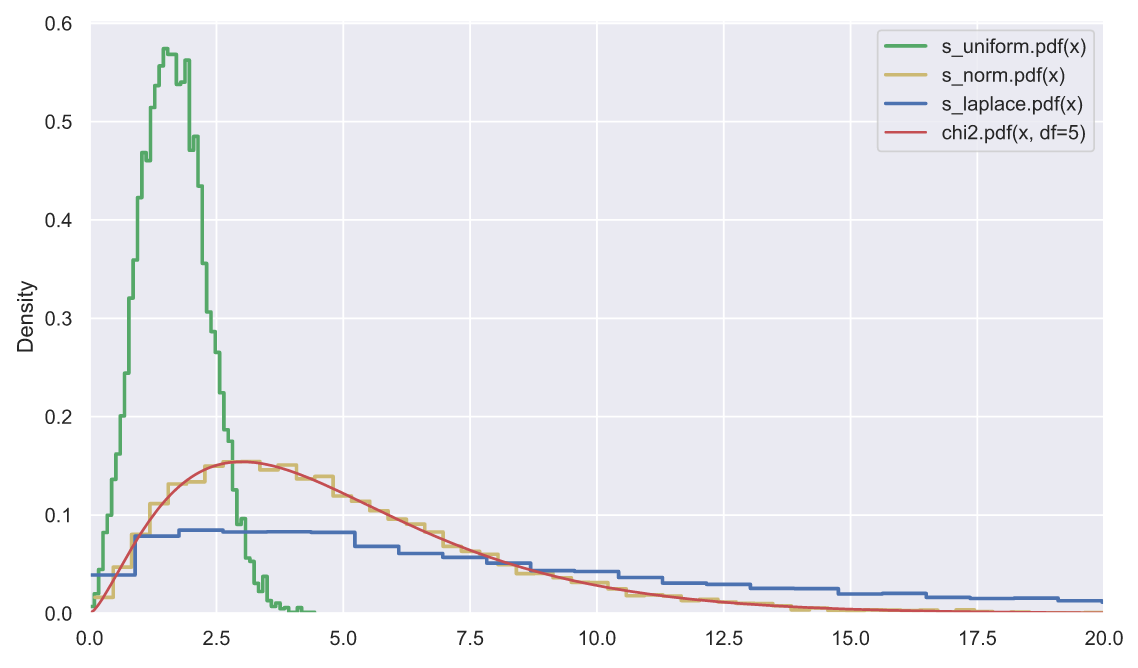
Для дисперсионного анализа нам крайне важно, чтобы суммы квадратов элементов выборки имели хи-квадрат распределение, как видите, это возможно, только если выборки взяты из "нормальной" генеральной совокупности. Если есть подозрения, что это условие не выполняется, то мы не можем использовать дисперсионный анализ, хотя мы по-прежнему можем пользоваться критерием Стьюдента для сравнения средних двух выборок (по-моему есть какая-то модификация критерия Стьюдента для сравнения средних произвольного количества групп).
А если нам все-таки нужен именно ANOVA, то как понять, что выборка взята из "нормальной" генеральной совокупности? Допустим, у нас есть вот такая выборка:
array([0.40572556, 0.67443266, 0.38765587, 0.96540199, 0.57933085])Согласитесь, что глядя на эту выборку очень трудно сделать какие-то выводы о ее принадлежности к тому или иному распределению. Что мы можем придумать? Давайте сгенерируем 50 тысяч выборок из нормального распределения по 5 элементов в каждой, отсортируем элементы в каждой выборке по возрастанию, а затем посмотрим, как распределены элементы в зависимости от индекса:
s = np.sort(stats.norm.rvs(size=(50000, 5)), axis=1).T
for i in range(5):
sns.histplot(x=s[i], stat='density',
label='i = ' + str(i),
element='poly', lw=2, fill=False)
plt.xticks(np.arange(-5, 6))
plt.legend();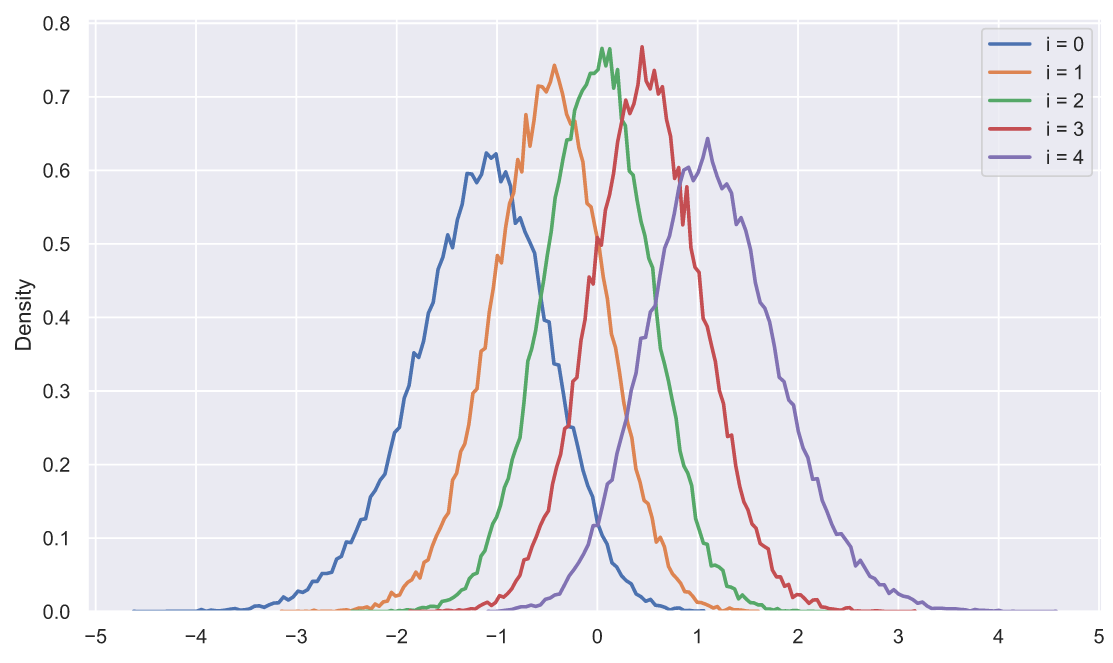
Любопытно, не правда ли? Оказывается, что отсортированные элементы распределены не одинаково, точнее все распределения имеют похожую форму, но отличаются сдвигом и масштабом. Наверное, мы могли бы сделать следующее:
"на глазок" прикинуть тип распределения;
подобрать параметры с помощью метода максимального правдоподобия;
рассчитать вероятность совместного отклонения элементов выборки от вершины каждого распределения (рассчитать статистику);
провести какое-то количество экспериментов, чтобы посмотреть как распределена плотность рассчитанной в предыдущем пункте вероятности (построить распределение статистики);
определить критическую область.
В принципе, у нас есть все шансы на то, чтобы придумать собственный критерий, который будет проверять гипотезу о том, что выборка взята из "нормальной" генеральной совокупности. Разве не круто?!! Например, мы можем даже визуально прикинуть вероятность того, что какая-то выборка принадлежит нормальному распределению:
s = np.sort(stats.norm.rvs(size=(50000, 5)), axis=1).T
sample = np.sort(stats.norm.rvs(size=5))
colors = sns.color_palette('tab10', 5)
for i in range(5):
sns.histplot(x=s[i], stat='density',
label='i = ' + str(i),
element='poly', lw=2, fill=False,
color=sns.color_palette('pastel', 5)[i])
plt.vlines(sample[i], 0, 0.8, lw=2, zorder=10,
color=sns.color_palette('tab10', 5)[i])
plt.xticks(np.arange(-5, 6))
plt.legend();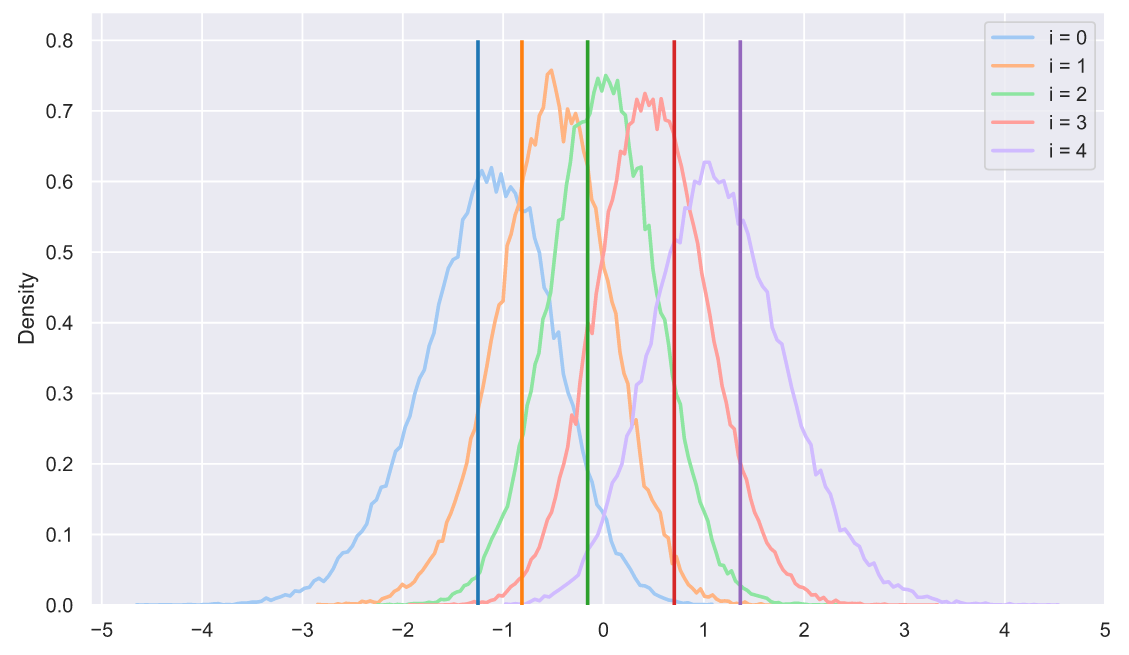
Или что какая-то выборка вряд ли принадлежит нормальному распределению:
s = np.sort(stats.norm.rvs(size=(50000, 5)), axis=1).T
sample = np.sort(stats.uniform.rvs(loc=-2, scale=4, size=5))
colors = sns.color_palette('tab10', 5)
for i in range(5):
sns.histplot(x=s[i], stat='density',
label='i = ' + str(i),
element='poly', lw=2, fill=False,
color=sns.color_palette('pastel', 5)[i])
plt.vlines(sample[i], 0, 0.8, lw=2, zorder=10,
color=sns.color_palette('tab10', 5)[i])
plt.xticks(np.arange(-5, 6))
plt.legend();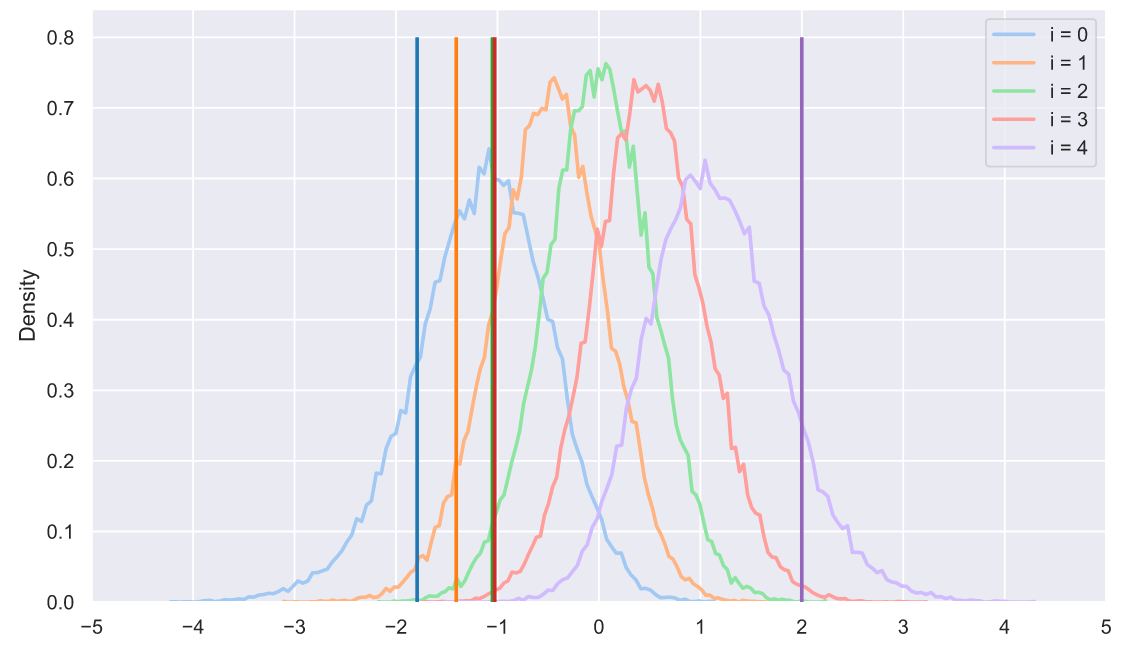
В общем, судя по всему мы действительно можем придумывать какие-то свои статистические тесты. Но согласитесь, все равно хочется думать, что внутри некоторых тестов происходит какая-то магия. Не зря их так много: десятки, может даже сотни. Не хочется верить в то, что все они устроены по такому простому принципу. Однако, это так. В качестве простого примера мы можем рассмотреть критерий Колмогорова:
stats.ks_1samp(x1, stats.norm.cdf, args=(5, 1.5))KstestResult(statistic=0.11452966409855592, pvalue=0.9971279018404035)В данном случае, чем меньше p-value, тем меньше вероятность того, что выборка взята из "нормальной" генеральной совокупности. А теперь давайте попробуем воспроизвести работу этого теста, который на самом деле не так уж и сильно отличается от того, что мы придумали выше. Для начала нам нужно вычислить эмпирические функции распределения вероятности и одну теоретическую, ту, с которой будет происходить сравнение:
x1.sort()
n = len(x1)
ecdf_ge = np.r_[1:n+1]/n
ecdf_le = np.r_[0:n]/n
cdf_teor = stats.norm.cdf(x1, loc=5, scale=1.5)
plt.plot(x1, ecdf_ge, color='b', drawstyle='steps-post', label='ecdf_ge')
plt.plot(x1, cdf_teor, color='r', drawstyle='steps-post', label='cdf_teor')
plt.plot(x1, ecdf_le, color='g', drawstyle='steps-post', label='ecdf_le')
plt.legend();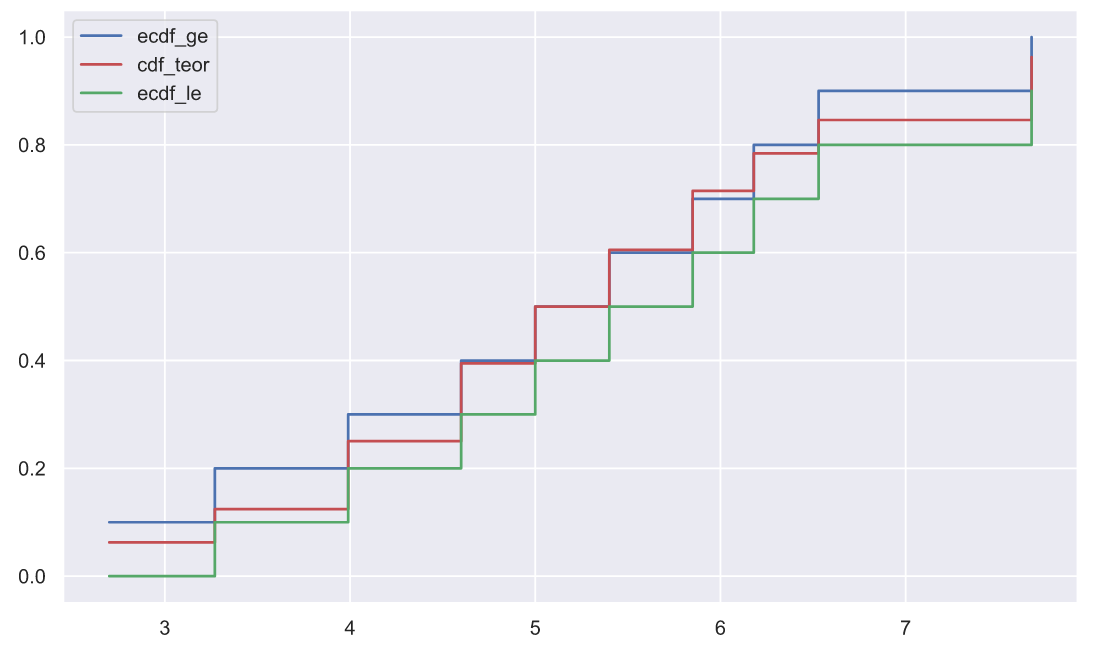
Статистикой в данном критерии является максимальная попарная разность между значениями эмпирических функций и теоретической, т.е. максимальная разность между красными и синими ступеньками или красными и зелеными ступеньками:
d_plus = ecdf_ge - cdf_teor
d_minus = cdf_teor - ecdf_le
statistic = np.max([d_plus, d_minus])
statistic0.11452966409855592Данная статистика имеет вот такое распределение плотности вероятности (попробуйте построить график при n=5):
x = np.linspace(0, 1, 3000)
plt.plot(x, stats.kstwo.pdf(x, n));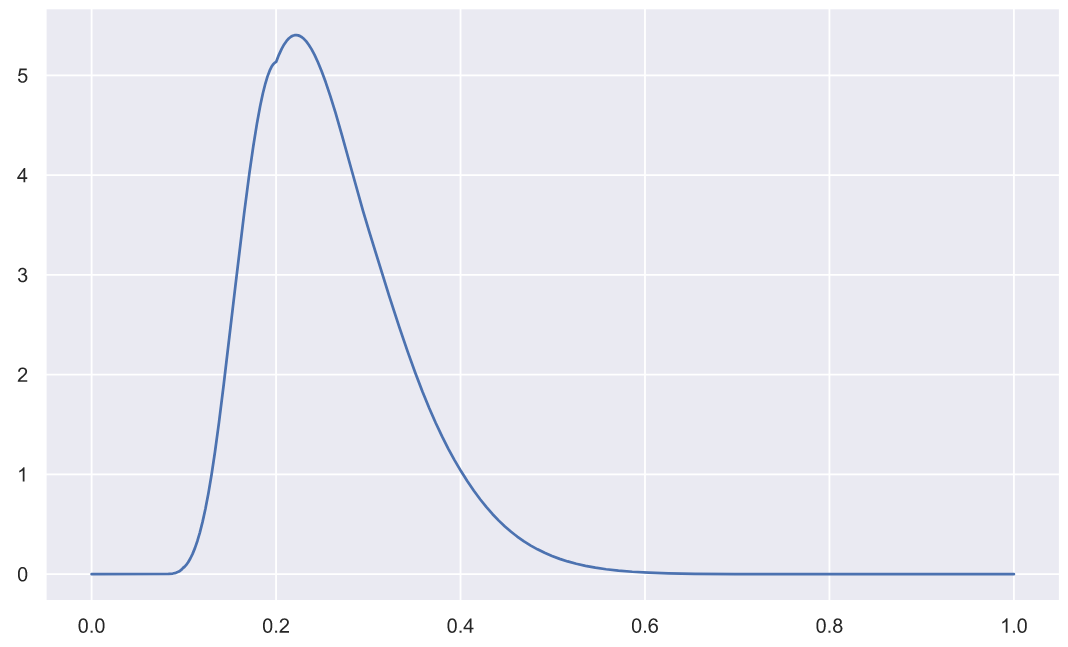
Благодаря которому мы можем вычислить значение p-value:
pvalue = stats.kstwo.sf(statistic, n)
pvalue0.9971279018404035Согласитесь, не так уж и сложно. Но надо признаться, что я так и не смог понять, что из себя пердставляет ecdf_le (есть только смутные представления). А то, что ecdf_le вообще должна присутствовать в вычислениях удалось понять только после просмотра исходников. Но тут же надо добавить, что моя "любовь" к статистике как раз и началась после того, как я полез в исходники seaborn, чтобы посмотреть, как вычисляются доверительные интервалы.
Напоследок
Наверняка, когда вы прочли о том, что одна половина группы программистов была отправлена на курсы онлайн-школы, а другая занималась самообразованием, то подумали: "Неужели автор опустится до холивара по поводу образования?" А если вы дочитали до конца, то подумали: "Зачем вообще было упоминать об этом, ведь в статье это нигде не используется?" Вместо ответа на первый вопрос, я дам вот эту ссылку. Вместо ответа на второй вопрос, задам свой - если результат исследований предсказуем или заранее известен, то может быть проблема не так глубока, может быть проблемы вообще не существует? Приступая к написанию этой статьи я действительно не знал, чем она закончится и какой она вообще должна быть. Стоит ли мне скрывать, что тема онлайн-образования вызывает во мне множество противоречивых чувств? Думаю, что нет.
Научные и технические статьи нельзя назвать легким чтивом, но писать их еще утомительнее. Хочется доносить какие-то сложные идеи в простой и непринужденной форме. Хочется надеяться, что у меня это хоть немного получается.
Тем не менее, как бы там ни было, мы еще продолжим погружение! В песне Эминема "My name is" у меня есть любимая строчка "I just drank a fifth of vodka — dare me to drive? (Go ahead)", которая очень хорошо подходит для описания всего дальнейшего погружения.
Как обычно жму F5 и жду ваших комментариев!

