Менеджерам компаний часто приходится брать на себя принятие решений по проектам, которые уже начаты (продолжаются). Так происходит, потому что существенно меняется состояние экономики, на рынке заключаются крупные сделки, которые меняют позиции ключевых конкурентов, или появляются радикально новые технологии, и продолжение проекта становится бессмысленным. Право отложить исполнение проекта, или изменить стратегию его реализации в литературе по финансовому менеджменту называют управленческим опционом (Managerial Option). Также в экономической литературе закрепился термин реальный опцион (Real Option), он четко отделяет это понятие от обычного финансового опциона.

Поскольку принятие решений в таких случаях неизбежно связано с вероятностными оценками и множеством неопределенностей, диаграммы влияния, как и все Байесовские сети доверия (БСД) чрезвычайно полезны для моделирования ситуаций и прогнозирования ожидаемых результатов. Рассмотрим два простых примера с реальными опционами, адаптированные из [2], в условия которых введены некоторые ограничения, позволяющие получить конечные численные решения. Как обычно, решаем задачи с использованием Netica, а попутно опробуем функцию программного заполнения таблиц полезности.

В первом примере компания рассматривает инвестиционный проект, планируемый к исполнению в пределах одного года. В момент времени t = 0 (начало года) у компании имеется  возможность выбора: произвести одну единицу изделия, или ликвидировать производство. Изделие планируется поставить на экспорт, поэтому существует неопределенность в отношении будущего обменного курса рубль/евро. Дополнительные условия таковы:

- производство одного изделия занимает весь год, и требует капитальных затрат в сумме 1,8 млн. руб.;

- изделие планируется продать (экспортировать) в конце года за 25 тыс. евро;

- в качестве альтернативы компания может ликвидировать производство, получив чистую ликвидационную стоимость 0,2 млн. руб. Однако если изделие выпущено, то производственные мощности не имеют ликвидационной стоимости;

- текущий спот курс обмена составляет 1 евро за 80 руб.;

- изменение курса обмена валют за один год задано с помощью мультипликатора М. На основе анализа состояния экономики и собственных ожиданий менеджеры компании считают, что в случае роста курса валюты мультипликатор М может измениться на величину u = 1,2; в случае снижения – на величину d = 0,8. По мнению менеджеров, вероятность роста курса валюты равна 60 %, соответственно, вероятность снижения составляет 40 %.

- безрисковые ставки для всех валют равны 5 %;

- для данного проекта ставка дисконтирования с учетом риска равна 10 %.

Диаграмму влияния для решения первой однопериодной задачи компания строит всего из трех узлов (Рис. 1):

- родительский узел случайной переменной состояния валютного мультипликатора М в конце года;

- узел решений, представляющий альтернативные варианты решения D: производить изделие (Produce), или ликвидировать производство (Liquidate);

- узел полезности, представляющий ожидаемые результаты принятия решений.

До инициализации модели стержневые диаграммы узлов не отображаются (Рис. 2), т.к. таблицы вероятностей и полезности еще не заполнены.

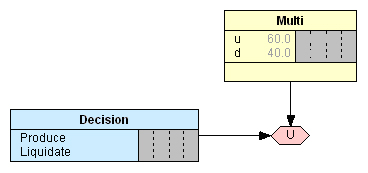
Поскольку узел состояния валютного мультипликатора М является родительским, для него составляется таблица безусловных вероятностей (ТБВ, Таблица 1) с учетом ожиданий компании, указанных выше.

Таблица 1. ТБВ для узла состояния М.

Далее необходимо заполнить таблицу полезности (Табл. 2). Здесь компания оценивает полезность проекта на основе классического показателя чистой приведенной стоимости (NPV). Если мультипликатор М изменится на величину u, то при курсе обмена 1 евро за 80 руб. значение NPV данного проекта определяется как разница дисконтированного денежного потока, ожидаемого в конце года, и капитальных затрат:

Если мультипликатор М изменится на величину d, то получим:

Отметим, что эти значения соответствуют варианту решения Produce. В случае альтернативного решения ликвидировать производство (Liquidate) по условию может быть получено только 0,2 млн. руб. при любом курсе валют.

Таблица 2. Состояния переменной узла полезности.

После заполнения всех таблиц остается инициализировать модель и приступить к анализу решений (Рис. 3). 

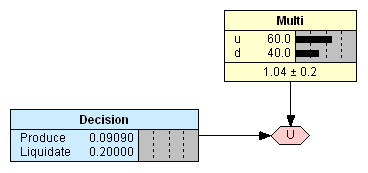
Для начала проверим, как машиной было получено значение ожидаемой полезности в строке Produce таблицы узла решения:

Е(Produce) = 0,6 · 0,382 + 0,4 · (- 0,346) = 0,0909 млн. руб.

Отсюда получаем решение, максимизирующее полезность:

Е(D) = max (0,0909; 0,2) = 0,2 млн. руб.

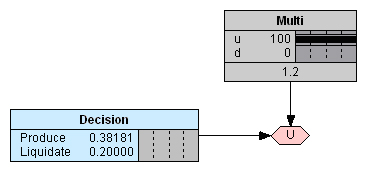
Таким образом, решением компании в условиях полной неопределенности должна быть ликвидация производства. Однако при поступлении свидетельства о том, что курс обмена валют вырастет, машина выдает другое значение, подтверждающее, что в таком случае решение о производстве изделия могло быть более выгодным (Рис. 4). 

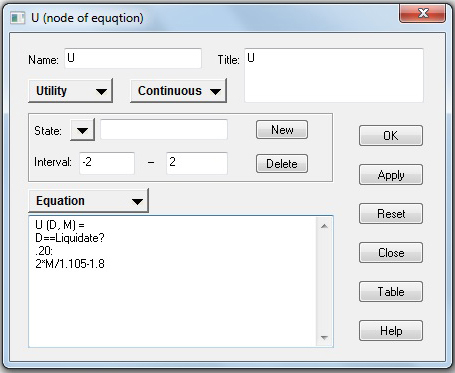
Программа Netica позволяет использовать готовые эмпирические зависимости, такие как функция NPV в данном примере, для того чтобы не считать вручную значения результатов в таблице полезности, а запрограммировать их расчет прямо в форме для ввода параметров узла. В частности, для данного примера можно задать функцию полезности следующим образом (Рис. 5):

U(D,M) =

D = = Liquidate?

.20:

2 * M/1.1-1.8

Или в псевдокоде:

Если (D = = Liquidate?), то U(D,M) = 0,2 иначе U(D,M) = 2 · М/1,1 – 1,8.

Далее используется функция меню Equation to Table, и результаты расчетов с более высокой точностью автоматически загружаются в соответствующие ячейки таблицы полезности. Для данного небольшого примера ускорение и уточнение расчетов может показаться незначительным, но далее в более сложной задаче мы увидим, что эта возможность дает неоценимые преимущества. 

В первом примере также интересно отметить, что если бы мы точно знали, что курс обмена валют вырастет, то рисковую процентную ставку можно было бы заменить безрисковой, и тогда положительный эффект от реализации проекта был бы еще сильнее. Это можно показать следующим образом:

В следующем примере горизонт инвестирования увеличивается до двух лет. В этом случае в момент времени t = 1, т.е., по прошествии первого года, у компании появляется опцион на выпуск еще одной единицы аналогичного изделия. Таким образом, компания может произвести одну единицу изделия в текущем году (t = 0), и одну единицу в следующем (t = 1). Уточним все параметры проекта:

- в каждом периоде производство одной единицы изделия занимает весь год, и затраты составляют 1,8 млн. руб.;

- в конце каждого периода каждое изделие может быть продано за 25 тыс. евро;

- в момент t = 0 компания может временно выйти из рынка с затратами 0,1 млн. руб. Это означает, что в момент t = 0 компания не начинает производство изделия. Если компания будет намерена производить изделие в следующем периоде, то ей придется заплатить 0,1 млн. руб. за вход на рынок;

- вместо начала производства в моменты t = 0 или t = 1 компания могла бы ликвидировать завод, получив чистую ликвидационную стоимость 0,2 млн. руб. Однако, если изделие производится в момент t = 1, то завод не имеет ликвидационной стоимости в момент t = 2;

- обменный курс, значения валютного мультипликатора, вероятности и процентные ставки остаются такими же, как в предыдущем примере.

Диаграмма влияния для новых условий задачи (Рис. 6) увеличивается как минимум до пяти узлов:

- родительский узел случайной переменной валютного мультипликатора М_0 для первого года (t = 0);

- родительский узел случайной переменной валютного мультипликатора М_1 для второго года (t = 1);

- узел решения D_0 для первого года (t = 0);

- узел решения D_1 для второго года (t = 1);

- узел полезности, представляющий ожидаемые результаты принятия решений. 

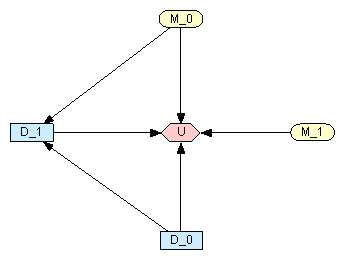
Варианты решений требуют отдельного пояснения. В первом периоде компания может принять одно из трех альтернативных решений D_0:

- производить изделие (Produce);

- ликвидировать производство (Liquidate);

- отложить реализацию проекта (Postpone), что отображено на диаграмме соответствующего узла решений (Рис. 7).

Если компания в первом периоде выбирает «производить» или «отложить», то через год она должна будет принять следующее решение. Во втором периоде отложить выполнение проекта уже нельзя (D_1), поэтому остаются только варианты «производить» или «ликвидировать». 

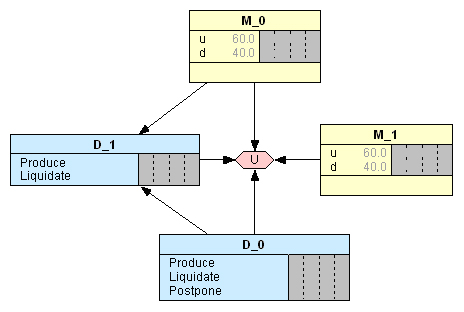
Поскольку узлы состояния валютных мультипликаторов М_0 и М_1 являются родительскими, для них составляются две одинаковые таблицы безусловных вероятностей (ТБВ, Таблица 3) с учетом ожиданий компании, указанных выше.

Таблица 3. ТБВ для узлов состояния М_0 и М_1.

Таблица полезностей увеличивается пропорционально количеству узлов (Табл. 4). Для ее заполнения необходимо заново рассчитать все значения NPV, учитывая следующие моменты:

Если компания производит изделие в двух периодах, и в обоих периодах курс валюты растет, то:

Если компания производит изделие в двух периодах, при этом в первом периоде курс валюты растет, а во втором снижается то:

Если компания производит изделие в двух периодах, при этом в первом периоде курс валюты снижается, а во втором растет, то:

Наконец, если при двух периодах производства курс валюты снижается, получим:

Если компания в первом периоде производит, во втором ликвидируется, при этом в обоих периодах курс валюты растет, то:

Если компания принимает решение в первом периоде отложить (postpone) реализацию проекта, а во втором возобновить производство, и в обоих периодах курс валюты растет, то:

Если компания решает в первом периоде отложить реализацию проекта, а во втором – ликвидировать завод, то:

 и т. д. В итоге можем заполнить всю таблицу полезности (Табл. 4)

Таблица 4. Состояния узла полезности.

Как и в предыдущем примере, всю таблицу полезности можно альтернативно заполнить с помощью вычисления функций NPV. Программный код будет выглядеть следующим образом:

U(D0,M0,D1,M1) =

D0 = = Liquidate?

.20:

D0 = = Produce && D1 = = Produce?

2*M0/1.1-1.8+2*M0*M1/1.1^2-1.8/1.1:

D0 = = Produce && D1 = = Liquidate?

2*M0/1.1-1.8+.2/1.1:

D0 = = Postpone && D1 = = Produce?

-.1-.1/1.1+2*M0*M1/1.1^2-1.8/1.1:

D0 = = Postpone && D1 = = Liquidate?

.1+.2/1.1.

В этом примере использование программируемых функций уже дает ощутимый выигрыш в компактности и точности вычислений. После завершения этой работы инициализируем модель, и можем приступать к вероятностным выводам (Рис. 8). 

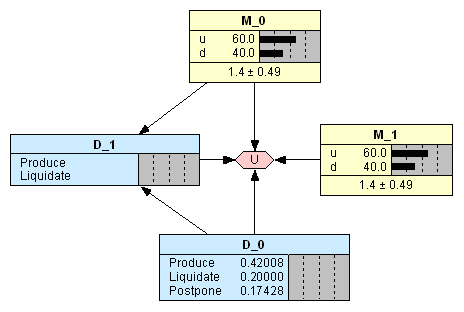
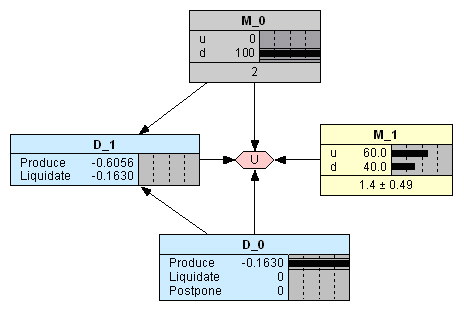
Предположим, компания принимает решение производить изделие в первом периоде, но при этом валютный мультипликатор принимает возможное значение d (Рис. 9). Для анализа решения компании в следующем периоде:

- кликаем узел решений D_0 в строке «Produce»;

- кликаем  узел мультипликатора М_0 в строке d.

Получаем на диаграмме узла решений D_1 результат (-0,1630 млн. руб.), подтверждающий меньшие потери при ликвидации завода. Отсюда следует вывод, что компании в таком случае следовало бы ограничить убытки этой суммой и выйти из бизнеса. Это и есть тот самый случай, когда инвестору бывает психологически трудно принять решение о ликвидации (выходе из проекта), и он остается в бизнесе, надеясь отыграть потери. 

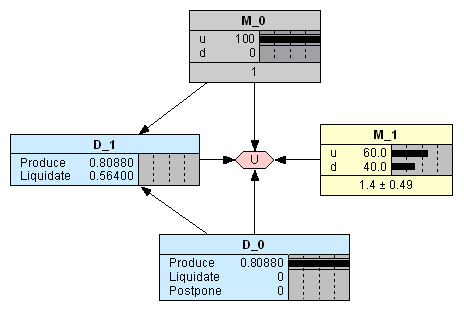
Далее предположим, что компания принимает решение производить изделие в первом периоде, но при этом валютный мультипликатор принимает возможное значение u (Рис. 10). В этом случае получаем подтверждение рекомендации продолжать производство, т.к. ожидаемый эффект (0,8088 млн. руб.) превышает эффект от ликвидации (0, 554 млн. руб.). 

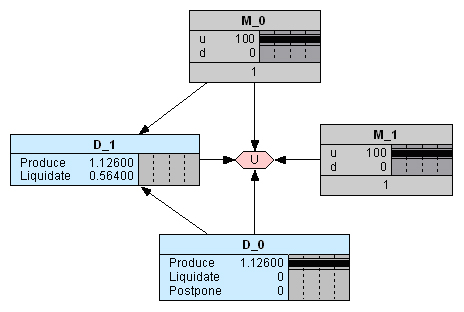
Если и на второй год валютный курс сохраняет тенденцию к росту (Рис. 11), то рекомендация усиливается еще более высоким ожидаемым эффектом (1,126 млн. руб.). 

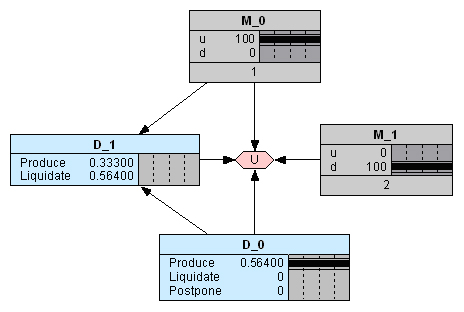
Наконец, если на второй год валютный курс снижается, то ликвидация вновь становится более выгодной: 0,564 млн. руб. > 0,333 млн. руб. (Рис. 12). 

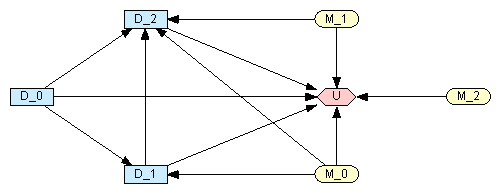
Пример двухпериодной задачи показывает, что таблица узла полезности растёт очень быстро, и её заполнение требует концентрации внимания. На Рис. 13 приведена схема графа для еще более интересной трёхпериодной задачи. В принципе, в ней уже нет ничего нового, но по количеству связей понятно, что таблица узла полезности будет размерами ещё больше. 

В связи с этим отметим, что программное заполнение таблиц полезности позволяет не только ускорить и уточнить расчеты, но еще и получить в задачах подобного типа дополнительную возможность исследования, например, чувствительности проекта к процентным ставкам. Перебор большого количества вариантов процентных ставок при этом можно не только ускорить, но даже автоматизировать. В частности, в первом примере легко проверить, что при ставках дисконтирования выше 15,55% производство становится убыточным при любых сочетаниях факторов неопределенности.

Литературы по данной теме имеется довольно много. Чаще всего для оценки реальных опционов пытаются адаптировать методики, изначально разработанные для оценки финансовых опционов, но это заставляет авторов вводить допущения, которые не лучшим образом отражаются на результатах. Логико-вероятностный подход встречается реже. Как обычно, привожу один отечественный и один зарубежный источник.

Литература

1.      Лимитовский М.А. Инвестиционные проекты и реальные опционы на развивающихся рынках. М.: Юрайт, 2019.

2.      Neapolitan R.E., Jiang X. Probabilistic methods for financial and marketing informatics. Morgan Kaufmann, 2007.