О своем трепетном отношении к Байесовским сетям доверия (БСД) я уже написал в предыдущей статье. Там же детально разобрана очень простая модель анализа решений инвестора об исполнении опциона колл на акцию. На этот раз предлагаю углубиться в тему и построить БСД, которая уже может послужить основой более серьезной модели поддержки принятия решений о покупке/продаже акции нефтяной компании.

Заранее отмечу, что я не придумывал этот пример, и даже укажу источник [1]. Однако в источнике, как это часто бывает, упущено множество подробностей, что оставляет осадок неудовлетворенности, а у студентов – просто непонимание, которое приводит к тому, что они перешагивают этот материал, так и не разобравшись в нем до конца. А задача стόит того, хотя бы потому, что в ней умело использованы почти все основные «хитрости» БСД, и если разобрать её «до винтика», то можно уверенно двигаться дальше.

Как известно, традиционные финансовые модели были сосредоточены на исторических и количественных связях между переменными. Однако на практике опытные финансовые аналитики всегда пытаются связать исторические данные с текущей рыночной информацией любого рода, и понять, как эта информация влияет на доходность акций, секторов рынка, на процентные ставки, и другие параметры, характеризующие модель портфеля. Например, в своё время антитрастовое расследование в отношении компании Майкрософт повлияло на доходность акций многих компаний, но оказалось, что такую информацию трудно учесть в традиционных моделях доходности [1]. Байесовские же сети, наоборот, легко воспринимают такие переменные в своей структуре.

Другим недостатком традиционных моделей является их статичность, часто невозможность уточнять результаты в процессе получения новой информации. Здесь также отметим, что способ представления переменных в БСД позволяет аналитику быстро вводить новую информацию, и сразу видеть ее влияние на всю сеть, а не только на конечный результат.

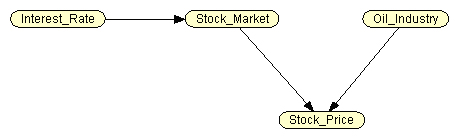
Итак, нас интересует состояние акции нефтяной компании. Построим БСД из четырех узлов, отображающих следующие случайные переменные (Рис. 1):

- Interest Rate (IR) – уровень процентных ставок (родительский узел);

- Stock Market (SM) – состояние фондового рынка;

- Oil Industry (OI) – состояние нефтяной отрасли (родительский узел);

- Stock Price (SP) – уровень цены акции исследуемой компании.

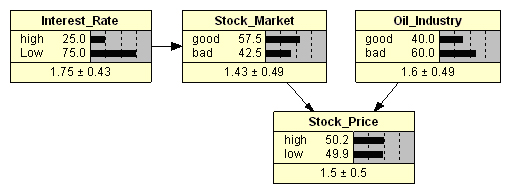
Все случайные переменные будут иметь по два дискретных состояния (Рис. 2). В частности, для левого родительского узла переменной процентных ставок назначены уровни: «высокий» и «низкий». Основываясь на собственном опыте и текущем состоянии рынка, эксперты считают, что в ближайшее время уровень процентных ставок с вероятностью 75% останется низким.

Правый родительский узел характеризует состояние нефтяной отрасли как «хорошее» или «плохое (тяжелое)». Как видим, здесь эксперты сходятся на том, что текущее состояние отрасли можно с вероятностью 40% считать хорошим. Установленные уровни вероятностей переменных в родительских узлах являются безусловными, они внесены в таблицы безусловных вероятностей (ТБВ), и отображаются на диаграммах соответствующих узлов (см. Рис. 2, только родительские узлы).

Вероятностные характеристики остальных переменных (наследников) мы «пока не видим» - они обусловлены состоянием родительских узлов, поэтому, для подтверждения значений полных вероятностей на их стержневых диаграммах нужно (по опыту предыдущей задачи) заполнить соответствующие таблицы условных вероятностей (ТУВ). Однако задача осложняется тем, что исходной информации для этого нет, поэтому эксперты должны использовать свои знания о закономерностях финансовых и сырьевых рынков, информацию о текущем состоянии этих рынков и других фактах и событиях, способных оказывать на них влияние.

Начнем с заполнения ТУВ узла состояния фондового рынка (см. Табл. 1). Эксперты реалистично учитывают, что при завышенных (растущих) процентных ставках фондовый рынок с большей вероятностью будет находиться в худшем состоянии, чем при низких (или средних) процентных ставках. По этой причине условной вероятности плохого состояния фондового рынка ври высоких процентных ставках присвоено значение 80%. Исходя из обратного утверждения (поскольку уровней всего два), условной вероятности хорошего состояния фондового рынка при низких процентных ставках присвоено значение 70%. В сумме вероятность реализации несовместных гипотез должна быть равна 100%, поэтому оставшиеся значения в ТУВ заполняем автоматически.

Таблица 1. ТУВ для узла состояния фондового рынка.

Заполнение ТУВ для узла переменной цены акции (см. Табл. 2) требует большего внимания, т.к. у этой переменной два состояния, и два родителя, у которых также по два состояния. Следовательно, в этой ТУВ будет 8 значений, поскольку необходимо «перебрать» все возможные вероятностные состояния этой переменной при всех вариантах состояний родительских узлов.

Начнем с того, что при одновременном хорошем состоянии фондового рынка и нефтяной отрасли (1-я строка ТУВ) уровень цены акции нефтяной компании с большей вероятностью должен быть высоким, поэтому ему присвоена вероятность 80%. Рассуждая от обратного, при одновременном плохом состоянии фондового рынка и нефтяной отрасли (4-я строка ТУВ) получаем самое низкое значение вероятности 10% для высокого уровня цены акции. Далее рассуждаем исходя из того, что при хорошем состоянии фондового рынка, даже при ухудшении ситуации в нефтяной отрасли (2-я строка ТУВ), цена акции конкретной компании может «по инерции» достаточно долго оставаться на высоком уровне, например, с вероятностью 60%. Наконец, учтем, что при ухудшении состояния фондового рынка состояние нефтяной отрасли не обязательно должно быть синхронно плохим (3-я строка ТУВ), и вероятностям уровней цены акции назначим 50/50.

Таблица 2. ТУВ для узла цены акции.

Таким образом, мы заполнили все ТУВ и после инициализации нашей БСД в программе Netica получаем априорное распределение вероятностей (Рис. 2), построенное машиной до поступления свидетельств. Обычно в этом месте у всех возникает одинаковый вопрос: как машина получила эти значения? Левое верхнее звено нашей БСД структурно очень похоже на предыдущую задачу с опционом, к тому же, у нас уже есть ТБВ и ТУВ, поэтому сразу делаем проверку:

SM good = 0,25 · 0,2 + 0,75 · 0,7 = 0,575

SM bad = 0,25 · 0,8 + 0,75 · 0,3 = 0,425

Всё сходится! Именно такие вероятности машина выдала на диаграммах узла фондового рынка. Значит, мы на верном пути, и можно двигаться дальше. Далее отметим, что этот узел, в свою очередь, является одним из родителей узла цены акции, а это значит, что полученные вероятности будут для него являться фактически безусловными с левой стороны.

У нас осталось самое сложное звено – сходящаяся тройка переменных, в которой два родителя влияют на одного потомка. Формально полная вероятность для такого случая в терминах нашей БСД будет выглядеть так:

P(SM, OI, SP) = P(SP| SM, OI) · P(SM) · P(OI)

Но при вычислении мы должны «перебрать» все значения вероятностей родительских узлов со всеми значениями условных вероятностей потомка. Не забывая, что слева (по графу) значения вероятностей родительского узла мы только что нашли, считаем, используя наши таблицы:

SP high = 0,8 · 0,575 · 0,4 + 0,6 · 0,575 · 0,6 +

                 0,5 · 0,425 · 0,4 + 0,1 · 0,425 · 0,6 = 0,5015

SP low = 0,2 · 0,575 · 0,4 + 0,4 · 0,575 · 0,6 +

                0,5 · 0,425 · 0,4 + 0,9 · 0,425 · 0,6 = 0,4985

Как видим (Рис. 2), именно такие значения полной вероятности (с учетом округлений) выдала машина на диаграмме узла цены акции. Таким образом, мы установили все структурные связи между переменными и заполнили все ТБВ и ТУВ, т.е. мы «обучили» модель, и можем использовать ее для вероятностных выводов в любом направлении.

В этой БСД, в силу ее большей сложности, возможны самые разнообразные выводы. Например, при поступлении свидетельства: «процентные ставки низкие» кликаем в строку «Low» узла процентной ставки (см. Рис. 3). При этом машина мгновенно пересчитывает вероятностное состояние узлов переменных фондового рынка и цены акции, в частности, вероятность роста цены акции увеличивается на 5,2% (до 55,4%). Отметим, что поскольку переменные «Уровень процентных ставок» и «Состояние нефтяной отрасли» являются независимыми (в данной  модели), состояние правого родительского узла не изменилось.

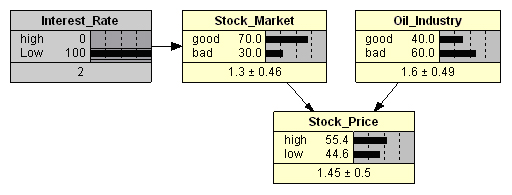
При низкой процентной ставке и поступлении свидетельства, подтверждающего, что «состояние нефтяной отрасли хорошее» (см. Рис. 4) вероятность роста цены акции увеличивается очень существенно – до 71%.

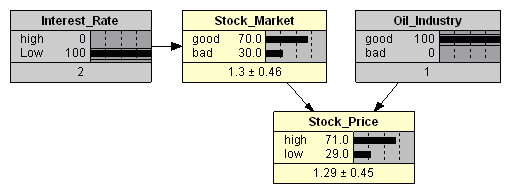
При поступлении свидетельств: «процентные ставки повысились» при «хорошем состоянии нефтяной отрасли» (см. Рис. 5) вероятность роста цены акции вполне закономерно снижается до 56%, но всё же остается высокой.

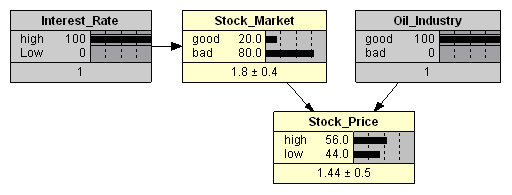
При высоких процентных ставках ухудшение состояния нефтяной отрасли (см. Рис. 6) значительно (до 80%) повышает вероятность снижения акций.

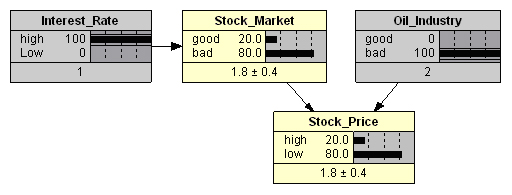
Наконец, при высоких процентных ставках, плохом состоянии нефтяной отрасли повышается и вероятность общего снижения фондового рынка (Рис. 7), что повышает вероятность резкого падения акций до 90%.

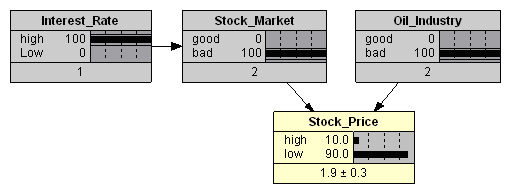
Вариантов выводов даже у этой простой модели действительно много, в чем предлагаю пытливому читателю убедиться самостоятельно. Возможности её «достройки» практически безграничны. Однако учебное время всегда ограничено, поэтому студенты обычно «уносят» эту задачу с собой на ноутбуках, а дома доводят её до ума, экспериментируют, добавляют новые узлы, увеличивают количество состояний переменных. Благо, что Netica, как, впрочем, и другие программы-редакторы БСД позволяет делать это буквально в один-два клика.

Помимо обещанного источника [1] также привожу совсем новую книгу [2], в которой много полезного по теме еще и в русском переводе.

Литература:

1.      Shenoy C., Shenoy P. Bayesian Network Models of Portfolio Risk and Return. Computational Finance. The MIT Press, 1999, pp. 87-106.

2.      Сукар Л. Вероятностные графовые модели. Принципы и приложения / пер. с англ. М.: ДМК Пресс, 2021.