Предыстория и введение

Как уже описывалось в предыдущей статье, в процессе переделки игрушки-осциллографа DSO138 возникла идея в DSO303 попробовать фокус с удвоением частоты дискретизации. В самом деле для STM32F303 теоретически максимально достижимая скорость дискретизации с точки зрения входа АЦП, а это определяется минимальным временем открытия УВХ, которое в нашем случае 1,5 такта х (1 / 72 МГц), или примерно 20,8 наносекунд, что дает 48 MSPS (миллионов отсчетов в секунду). Однако при параллельной работе 4-х АЦП на 6 МГц получается достичь только 24 MSPS из-за ограниченного быстродействия АЦП.

Представим себе, что мы рассматриваем правильно-периодический сигнал, который при этом еще и постоянен, т.е. не испытывает флуктуаций по частоте и амплитуде во времени. Возможно ли как-то оцифровывать его не в один, а в несколько проходов, тем самым увеличив эффективную частоту выборки? 

Оцифровка в три прохода – идея

Обратимся к Рис.1., на котором собственно и отображена идея многопроходной оцифровки. Предположим, что каждый АЦП запускается своим сигналом от таймера, который работает с удвоенной тактовой частотой микроконтроллера и АЦП (для 32F303 – 72 и 144 МГц соответственно). При этом цикл оцифровки занимает 12 тактов АЦП (24 такта таймера) при разрешении 10 бит. Поделим этот цикл на 8 слотов по 3 такта таймера (1,5 такта АЦП), что как раз соответствует времени открытия УВХ.

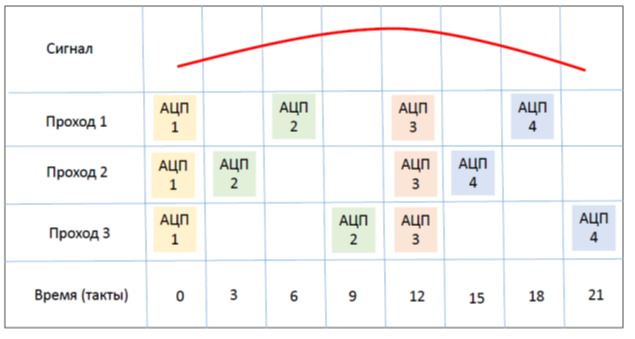
Каналы АЦП 1 и АЦП 3 сделаем референсными, они будут срабатывать всегда в одно и то же время цикла, а время срабатывания каналов АЦП 2 и АЦП 4 будем двигать внутри цикла в зависимости от прохода. Вот собственно и все, после выполнения 3-х проходов такой оцифровки мы получим конечный результат.

«Однако», - скажет внимательный читатель: «но позвольте, почему вы предполагаете, что ваш цикл оцифровки в следующем проходе будет находиться в неизменном положении по отношению к сигналу? Ведь старт процесса оцифровки происходит в случайный момент времени…». И, конечно же, он будет совершенно прав.

Но для этого у нас есть два референсных канала из четырех имеющихся, и время, чтобы запускать процесс оцифровки неограниченное количество раз. Надо просто запускать очередной проход много раз до того момента, когда положение цикла оцифровки относительно сигнала не окажется достаточно близким к тому, которое было при первом проходе, проверяя корреляцию по референсным каналам. Таким образом наш процесс оцифровки будет выглядеть следующим образом:        

1. Оцифровали и записали данные Прохода 1;

2. Оцифровали данные Прохода 2;

3. Посчитали корреляцию референсных каналов, если она достаточно хорошая, то записали данные Прохода 2, если нет, то повторяем п.2;

4. Оцифровали данные Прохода 3;

5. Посчитали корреляцию, если все хорошо, то записали данные и приступили к итоговой сборке и обработке данных оцифровки и отображению полученной картинки, если нет, то повторяем оцифровку Прохода 3. 

Результаты

Да, в итоге иногда процесс занимает довольно длительное время, и оцифровка может повторяться десятки тысяч раз, прежде чем достигается результат; да, далеко не для всех сигналов такой способ подходит; да, результат бывает не без искусственных артефактов как на Рис.2., но достаточно часто получается и как на Рис.3. На обеих рисунках на вход подан меандр частотой 1 МГц.

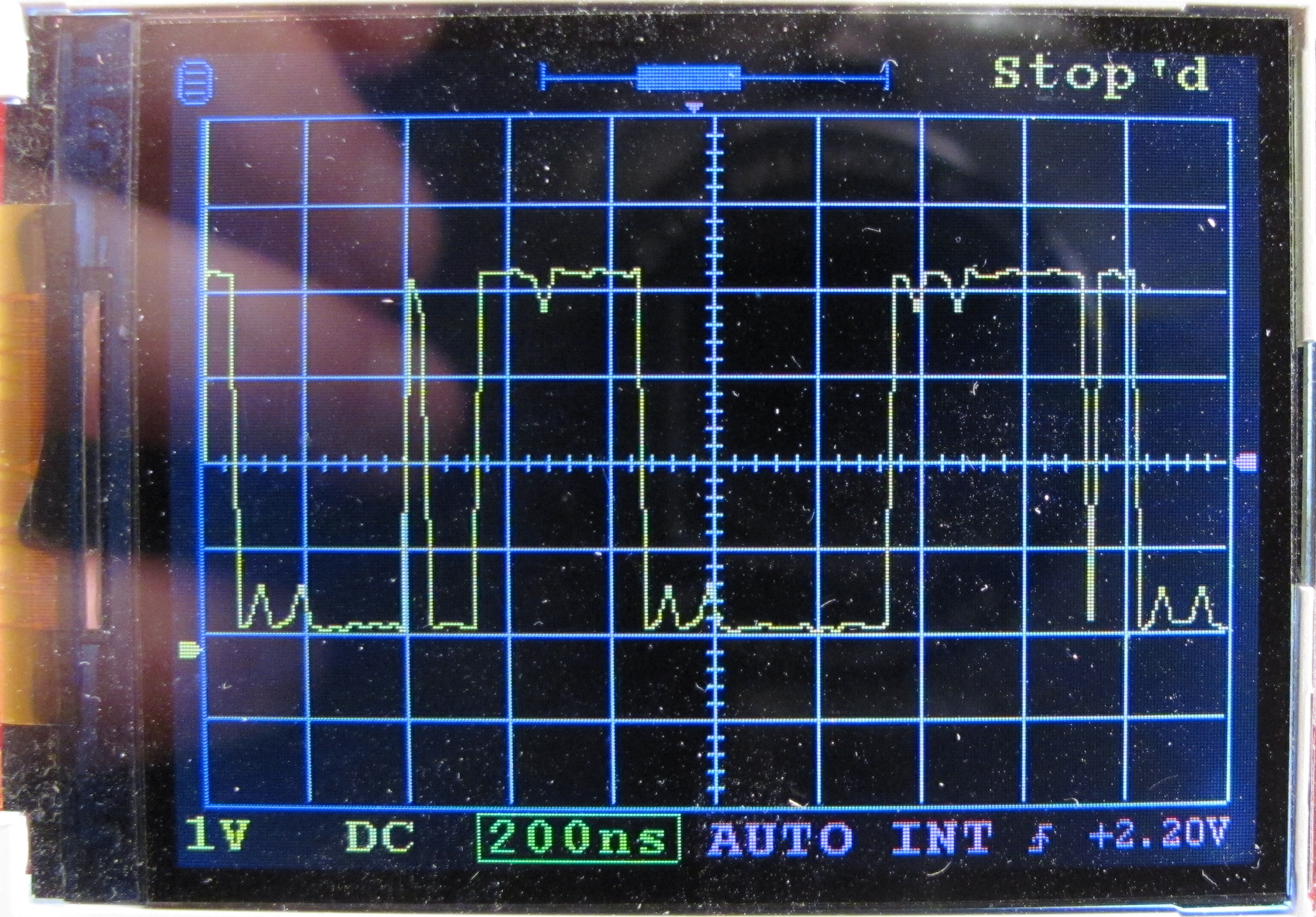
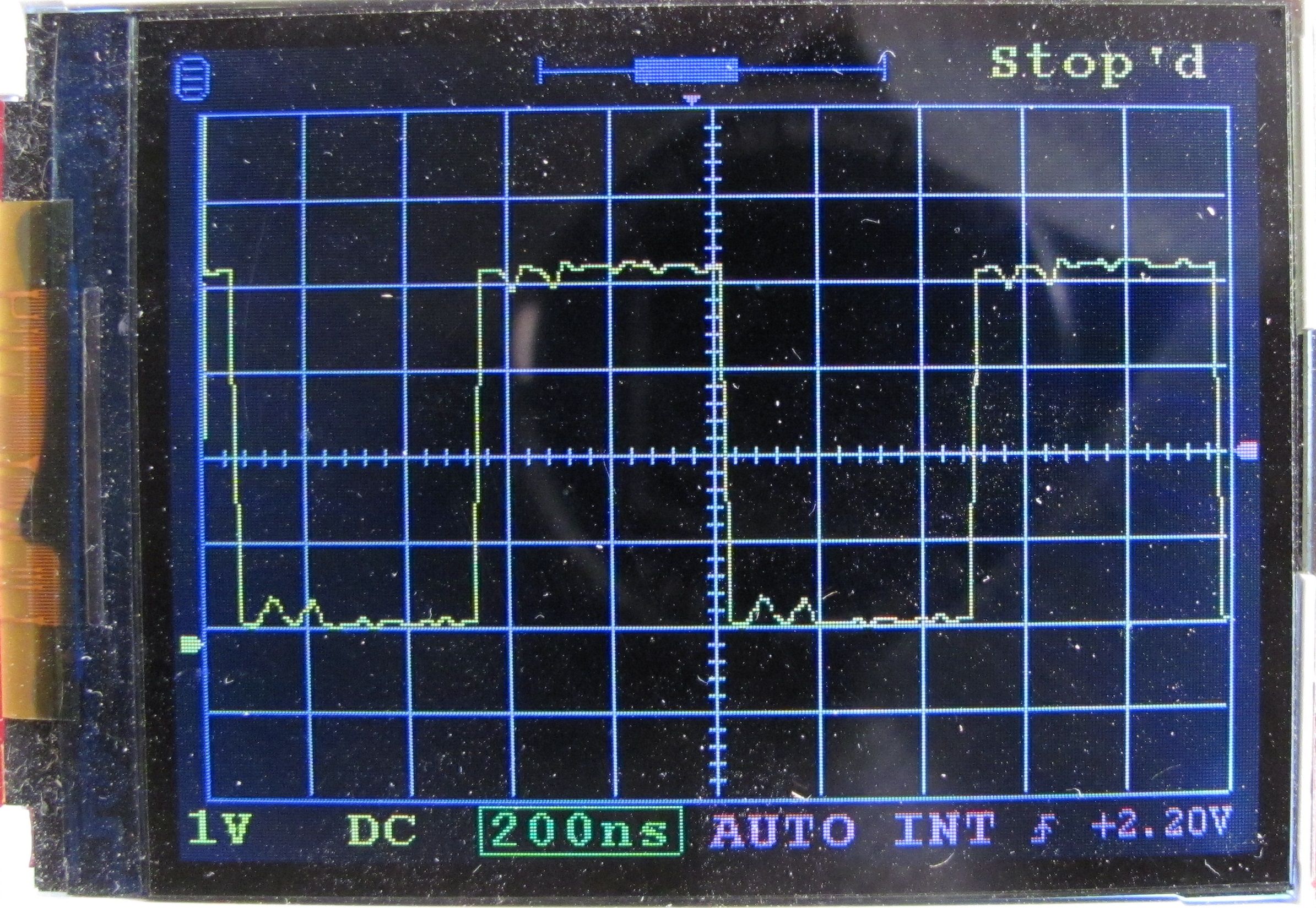
При этом хуже всего результаты получаются для сигналов с быстрыми изменениями формы и резкими фронтами (меандр), а наилучшие результаты наблюдаются для плавных сигналов (синусоида). Для иллюстрации на Рис.4 приведена также картинка синусоидального сигнала частотой 200 кГц. Сигнал там «немножко» шумный, с небольшими помехами, что сразу же приводит, к сожалению, к довольно большим искажениям в виде такой своеобразной "бороды", так как одним из условий корректной картинки при таком способе оцифровки, которое было уже упомянуто выше, является постоянство и отсутствие флуктуаций сигнала во времени, что эта картинка также и иллюстрирует.

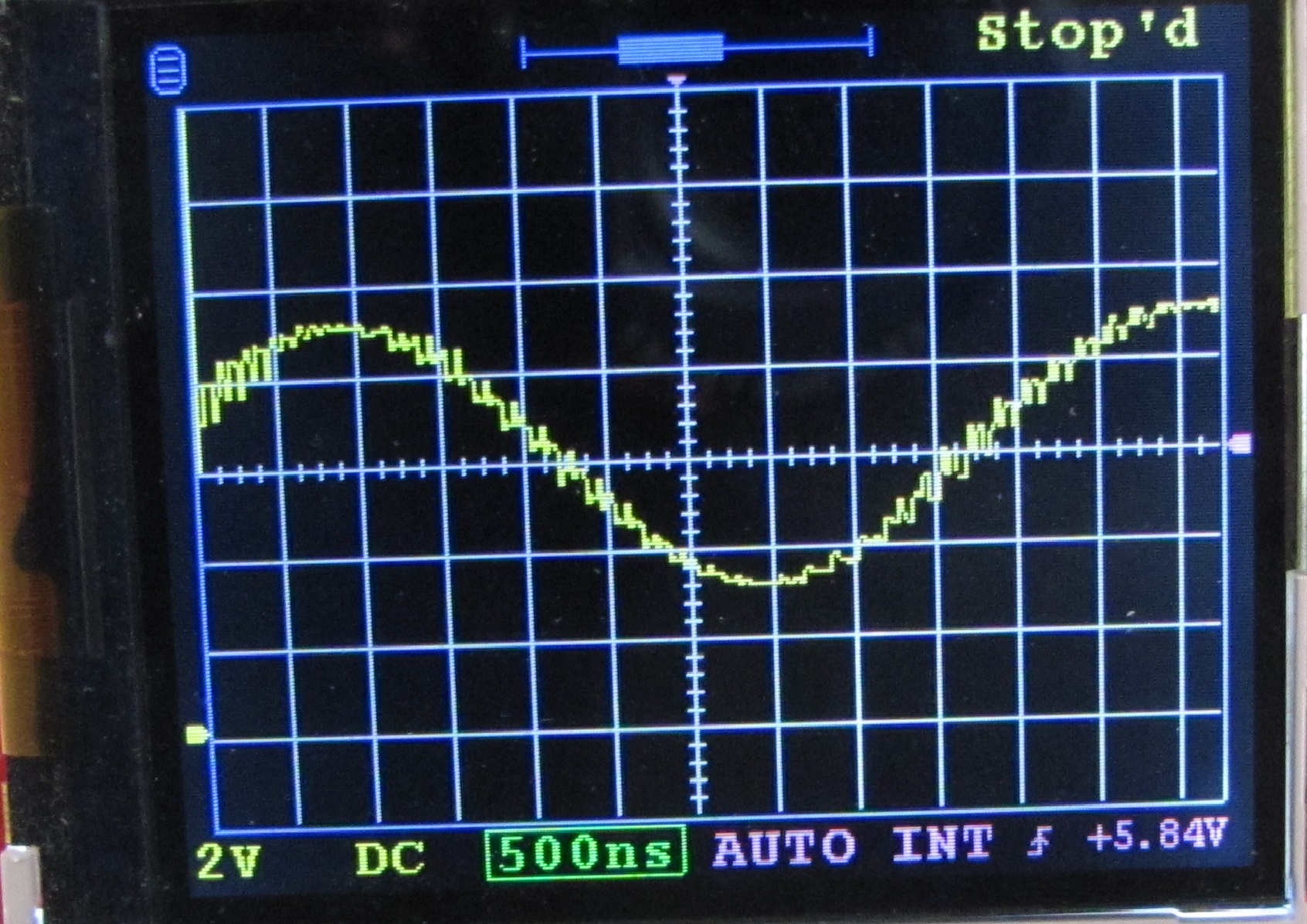
Период сигнала для правильной работы алгоритма корреляции теоретически не может быть меньше цикла оцифровки, практически приемлемый результат получается только при периодах сигнала больших 3-х циклов, т.е. >500 наносекунд. Таким образом рассматривать сигналы с частотами более 2-х МГц, к сожалению, все равно не получится. Но при этом хотя бы такие сигналы можно увидеть достаточно подробно, что несомненно будет полезным.  

Вот так DSO303 получил времена развертки 500 и 200 наносекунд на клетку. В режиме 500 наносекунд на клетку изображение – это честный результат оцифровки, каждая точка = отсчет. Далее я подумал, что неплохо бы было это изображение еще и растянуть, так появился режим 200 наносекунд на клетку. Для него используются ровно те же данные, что и для развертки 500 наносекунд на клетку, только они растянуты так, что один отсчет = 3 точкам на экране. Это оказалось довольно удобно и получило свое право на жизнь.

Все приведенное выше является экспериментальной идеей. Автор не претендует на полную работоспособность этого экспериментального способа оцифровки, и не несет ответственности за результат. Любые вопросы, замечания и предложения приветствуются.