
Машинное обучение все чаще используется аналитиками для упрощения работы при решении текущих задач, для реализации новых проектов или для выявления каких-либо ошибок и отклонений.
На данный момент одной из лидеров в машинном обучении для многих задач является библиотека XGBoost, основанная на алгоритме дерева решений и реализующая методы градиентного бустинга. Почему? Библиотека наиболее эффективна при построении моделей предсказания на структурированных больших данных, XGBoost поддерживает реализацию на Hadoop, имеется встроенная регуляризация и правила для обработки пропущенных значений, а также с помощью множества настроек можно улучшать качество прогнозирования модели за кратчайшие сроки, ведь имеется возможность параллельной обработки.
Немного о градиентном бустинге
При GB строятся последовательно уточняющие друг друга элементарные модели, последняя из которых обучается на ошибках предыдущих и ответы моделей суммируются.
По сравнению с GB XGBoost реализует параллельные вычисления, что значительно ускоряет обучение. XGBoost, позволяет пользователям настраивать цели оптимизации и критерии оценки, имеет встроенные правила для обработки пропущенных значений. Особенностями также является использование второй производной функции потерь — встроенная регуляризация, которая помогает предотвратить переобучение. XGBoost применяется для задач классификации, регрессии, упорядочения и ряда других. Наиболее эффективен данный алгоритм при построении моделей предсказания на структурированных больших данных.
Нами была построена модель на XGBoost для задачи предсказания уровня дохода клиентов. Ниже представлен код на Python:
train = pd.read_csv('train.csv',sep=';', encoding = 'windows-1251', decimal = ',')
test = pd.read_csv('test.csv',sep=';', encoding = 'windows-1251', decimal = ',')
oot = pd.read_csv('oot.csv',sep=';', encoding = 'windows-1251', decimal = ',')
#Выбираем x, y и убираем столбцы с известными значениями во избежание переобучения:
train_y = np.log(train['TARGET_INCOME'])
train_x = train.drop('TARGET_INCOME',axis =1)
train_x = train_x.drop('INCOME_XGBOOST',axis =1)
test_y = np.log(test['TARGET_INCOME'])
test_x = test.drop('TARGET_INCOME',axis =1)
test_x = test_x.drop('INCOME_XGBOOST',axis =1)
#Наконец можно импортировать модуль xgboost, выставить необходимые параметры и начать обучение модели. На этих данных модель обучается правильно предсказывать.
%%time
from xgboost import XGBRegressor
model = XGBRegressor(
booster = 'gbtree',
colsample_bylevel = 0.5,
colsample_bytree = 0.7,
subsampple = 0.8,
gamma = 0.0,
learning_rate = 0.02,
max_depth = 10,
n_estimators = 5000,
n_jobs = -1,
seed = 555)
model_top.fit(train_x[my_features], train_y, eval_set = [(train_x[my_features], train_y), (test_x[my_features], test_y)], eval_metric = 'rmse', verbose = 100, early_stopping_rounds = 50)Итак, модель обучена и можно проверить ее качество с помощью ошибки rmse. Соответственно, чем она меньше, тем лучше. У нас получилось не самое хорошее качество модели (rmse_train=0.37; rmse_test=0.47; rmse_oot=0.48), что можно исправить, попробовав подобрать подходящие фичи. Для этого выводим топ-30 фичей, на которых обучилась модель, чтоб понимать какие столбцы внесли больший вклад в обучение следующим кодом:
feature_names = train_x.columns
f_imp = model.feature_importances_
features_and_imp = pd.DataFrame([[feature_names[i], f_imp[i] for i in range(len(feature_names))])
max_features = features_and_imp.sort_values(by = 1, ascending = False)
max_features[:30]Немного поэкспериментировав с фичами, были получены меньшие ошибки: rmse_train=0.361; rmse_test=0.468; rmse_oot=0.475.
Вуаля, теперь наша модель может предсказать уровень доходов клиентов:
train_xtop = train_x[my_features]
test_xtop = test_x[my_features]
oot_xtop = oot[my_features]
pred_train = model_top.predict(train_xtop, ntree_limit = model_top.best_ntree_limit)
pred_test = model_top.predict(test_xtop, ntree_limit = model_top.best_ntree_limit)
pred_oot = model_top.predict(oot_xtop, ntree_limit = model_top.best_ntree_limit)После чего можно приступать к валидации. Существует множество валидационнных тестов для проверки качества работы модели. Для моделей градиентного бустинга разумно использовать следующие:
Анализ REC-кривой модели
Данный тест проводится для оценки точности модельных оценок регрессии относительно базового прогноза. В качестве базового прогноза может рассматриваться как простейшая статистическая конструкция (среднее, медианное значение выборки для разработки), так и
Для сравнения регрессионных моделей между собой или с базовым прогнозом производится построение REC-кривых. Для оценки ошибки могут быть использованы различные метрики (например, MSE или MAD). Производится расчёт площади над кривой (AOC – Area Over Curve) как для исследуемой модели, так и для базового прогноза. Оценка качества производится на основании отношения
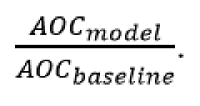
График REC-кривой показывает точность модели в зависимости от допустимого размера ошибки (долю наблюдений, для которых значение ошибки меньше, чем откладываемое по горизонтальной оси). Площадь над REC-кривой асимптотически равна математическому ожиданию ошибки, что позволяет использовать данную метрику для сопоставления моделей. Таким образом, если площадь над REC-кривой модели

превышает площадь над кривой базового прогноза

можно сделать вывод о том, что точность модели хуже, чем у базового прогноза. Также помимо сравнения ошибки модели с базовым прогнозом, представленная графическая визуализация позволяет анализировать качество моделей посредством скорости накопления точности модельных оценок в зависимости от уровня ошибки. В случае пересечения REC-кривых, лучшая модель может определяться не только площадью
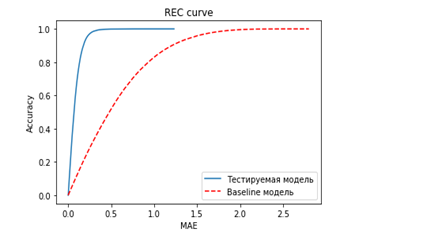
над REC-кривой, но и бизнес-смыслом задачи.
В нашем случае график показывает очень хорошую точность модели:
Коэффициент корреляции Спирмена
Данный тест нужен для оценки предсказательной силы модели в терминах ранговой корреляции между прогнозными и фактическими значениями целевой переменной.
Коэффициент ранговой корреляции Спирмена рассчитывается по формуле:

Необходимо отметить, что часто используемый на практике метод расчёта коэффициента является некорректным в общем случае, и может быть использован только тогда, когда все прогнозные значения целевой переменной различны (аналогично для фактических значений).

Тест позволяет оценить степень согласованности модельных и фактических значений, однако никак не оценивает точность оценок. Дополнительно приводится визуализация – строится график разброса (scatter plot), где по оси X отложены фактические значения, а по оси Y – соответствующие им модельные.
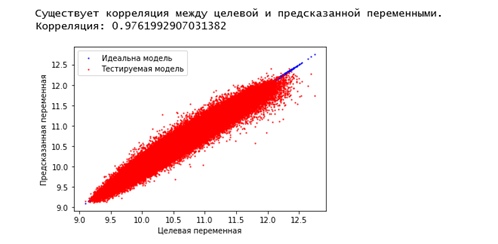
Вот так выглядит график разброса для нашей модели:
Анализ кривой learning curve
Кривая learning curve – это график изменения скорости обучения модели. То есть данный тест показывает изначальную сложность обучения.
В нашем случае модель показывает хороший результат:
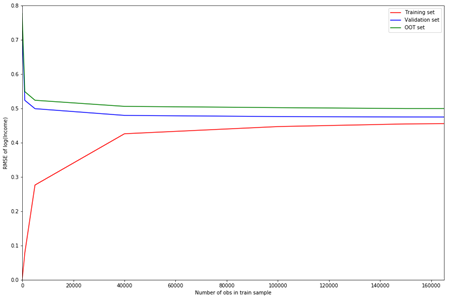
Также еще были проведены: тест на актуальность данных, анализ репрезентативности выборок, которые тоже показали достойные результаты.
Исходя из валидационных тестов, мы видим, насколько близки предсказанные моделью данные и исходные. Таким образом, у нас удалось получить модель предсказания уровня доходов клиентов с приемлемым для наших целей качеством. С помощью данной модели были проанализированы такие показатели как возраст, пол, количество операций пополнения счета, сумма всех выданных кредитов, сумма операций переводов, регион по серии документа, средний размер операции оплаты мобильной связи, медианный баланс по дебетовым картам, общая сумма всех поступлений по всем картам клиента, доход по клиенту, средняя операция пополнения счета, расходы на продукты, тип населенного пункта и предсказан уровень дохода каждого клиента из выборки, что позволило формировать более подходящие предложения каждому клиенту.
Итак, стоит отметить, что всегда нужно правильно подбирать валидационные тесты для каждого типа моделей. Важно понимать, что тесты, созданные для моделей бинарной классификации (макрокоэффициент Джини, динамика макрокоэффициента, Precision-Recall кривая и некоторые другие) не могут быть использованы для моделей регрессии и градиентного бустинга, и наоборот. То есть если провести тесты, не подходящие для модели XGBoost, то можно получить плохой результат, который на самом деле не отражает настоящую ситуацию. Как говорится, не зная броду, не суйся в воду

