Привет, Хабр! С недавнего времени я стал задумываться об актуальности статей и заметил, что на Хабре нет ни одной обзорной статьи про магнитные цепи. Как так!? Ведь это... а что это такое?

Действительно, наверняка даже самые отстраненные от инженерного дела люди имеют представление о том, что такое электрические цепи, но возможно, что про магнитные цепи не слышали вовсе. Каждый школьник когда-то в учебнике физики наблюдал разные схемы и формулы, описывающие законы Ома. Но магнитные цепи в рамки школьного курса не входят.

Я решил написать данную статью, чтобы показать, насколько удивителен мир физики и заинтересовать школьников в её изучении. В данной статье, однозначно, для полноты вещей будут и выводы формул и использование некоторых математических операций, которые могут быть известны не всем, но такие моменты я постараюсь сгладить. Приступим!

Что нужно вспомнить?

Для более четкого представления сей статьи, неплохо бы вспомнить основные характеристики самого магнитного поля: вектор магнитной индукции, вектор напряженности, поток вектора магнитной индукции - а также нужно вспомнить немного про магнитные вещества, а именно про ферромагнетики.

Полагается, что вам известен обобщенный закон Ома и помнится, что такое ток, напряжение и сопротивление. Если нет, то крайне советую обратиться к сторонним ресурсам, чтобы иметь хотя бы общее представление о том, что последует далее. Крайне советую учебник И.Е. Иродова «Электромагнетизм».

Применение магнитных цепей

Магнитные цепи находят очень большое поле применения, а именно, они используются для надежного пропускания магнитного потока по специальному проводнику с минимальными или, в некоторых случаях, определенными потерями. В электротехнической промышленности широко используется взаимная зависимость магнитной и электрической энергий, переход из одного состояния в другое. На подобном принципе работают, например, трансформаторы, разные электродвигатели, генераторы и другие устройства.

Конечно, можно продолжительное время говорить об устройствах, разных типах магнитопроводов (про которые речь пойдет далее), но наша первичная цель - рассмотреть выводы основных характеристик магнитных цепей. Продолжаем!

Как устроены магнитные цепи?

Магнитную цепь, на самом деле, не так сложно представить, как может показаться человеку, который о них впервые слышит. Обычно магнитные цепи представляют из себя некоторые фигуры из ферромагнитного сердечника с источником или несколькими источниками ПОтока. Пожалуй, один из самых простых примеров с одним источником, который можно взять на вооружение, проиллюстрирован ниже:

Перед продолжением обусловимся, что среди электротехников сердечник называют магнитопроводом. Часть магнитопровода, на которой отсутствуют обмотки и которая служит для замыкания магнитной цепи, называется «ярмо».

Начнем с тороидального сердечника. Такой тороидальный сердечник может служить формой для катушки, как бы странно это не звучало. Но что за катушка? Ну, первое что приходит в голову - провод, образующий витки. Хорошо, но какого его предназначение? Вернемся к электрическим цепям и вспомним, что существуют источники тока / напряжения, так называемые активные элементы. Так вот, в магнитных цепях роль источника выполняют катушки с током, накрученные на основной элемент магнитной цепи - ферромагнитный магнитопровод.

Вспомним теперь про ферромагнитные материалы. Почему именно они? Дело в том, что благодаря высокому значению магнитной проницаемости, что сигнализирует о хорошей намагниченности ферромагнетика, силовые линии магнитного поля практически не выходят за пределы сердечника, либо не выходят вовсе. Однако это будет справедливо лишь тогда, когда наш сердечник замкнутый, либо имеет небольшие зазоры. То есть, ферромагнетики обладают сильно выраженными магнитными свойствами, когда как у парамагнетиков и диамагнетиков они значительно слабее, что можно наблюдать на следующем графике зависимости намагниченности от напряженности магнитного поля:

Вещества, которые входят в конструкцию магнитопровода, могут обладать не только сильномагнитными свойствами, но также и слабомагнитными. Однако мы рассматриваем сердечник из ферромагнитного материала.

Ещё из школьного курса мы представляем себе картину с линиями магнитной индукции соленоида, мы можем визуально представить его поле и понимаем, что концентрация силовых линий, их насыщенность, наибольшая в центре рассматриваемого соленоида. Тут очень важно вспомнить правило буравчика, чтобы правильно указать направление силовых линий.

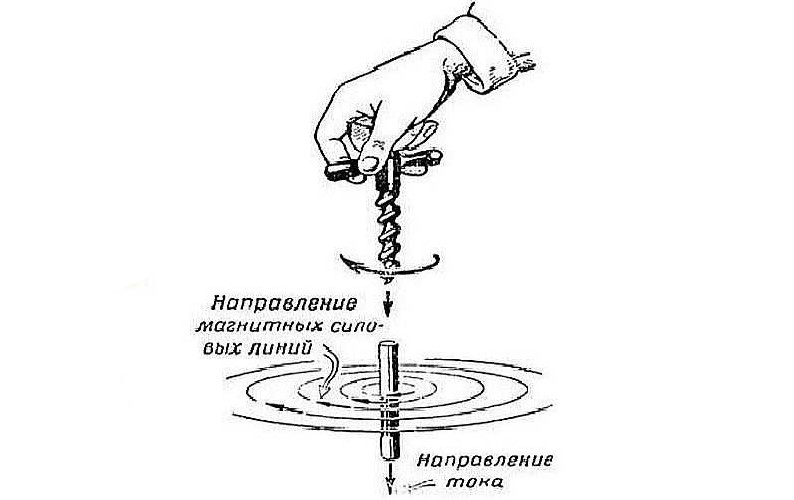
Отсюда становится ясно, что катушки-источники порождают магнитное поле, а следовательно и поток линий магнитной индукции. Такие линии будут циркулировать по нашему сердечнику, словно повторяя его форму. Именно поэтому нам важно условие замкнутости сердечника и материал, из которого он сделан. Положим, что наш воображаемый сердечник замкнут. Из этого следует, что и силовые линии замкнуты, а следовательно выполняется теорема Гаусса для магнитного поля, которая гласит: поток линий магнитной индукции через замкнутую поверхность равен нулю. Стоит учесть, что поток адаптируется под площадь сечения.*

Ну и в конечном счете ферромагнитный сердечник поток куда-то передает! Аналогичным образом замкнутый проводник позволяет передать электрический ток.

Отлично! Мы разобрались с тем, что такое магнитные цепи и даже вспомнили про теорему Гаусса и ферромагнетики. Теперь поговорим о том, какие следствия вытекают из теоремы Гаусса и возможности пренебрежения полем вне сердечника и в зазорах.

1] Магнитные потоки Ф₁ и Ф₂ через произвольные сечения будут равны между собой.

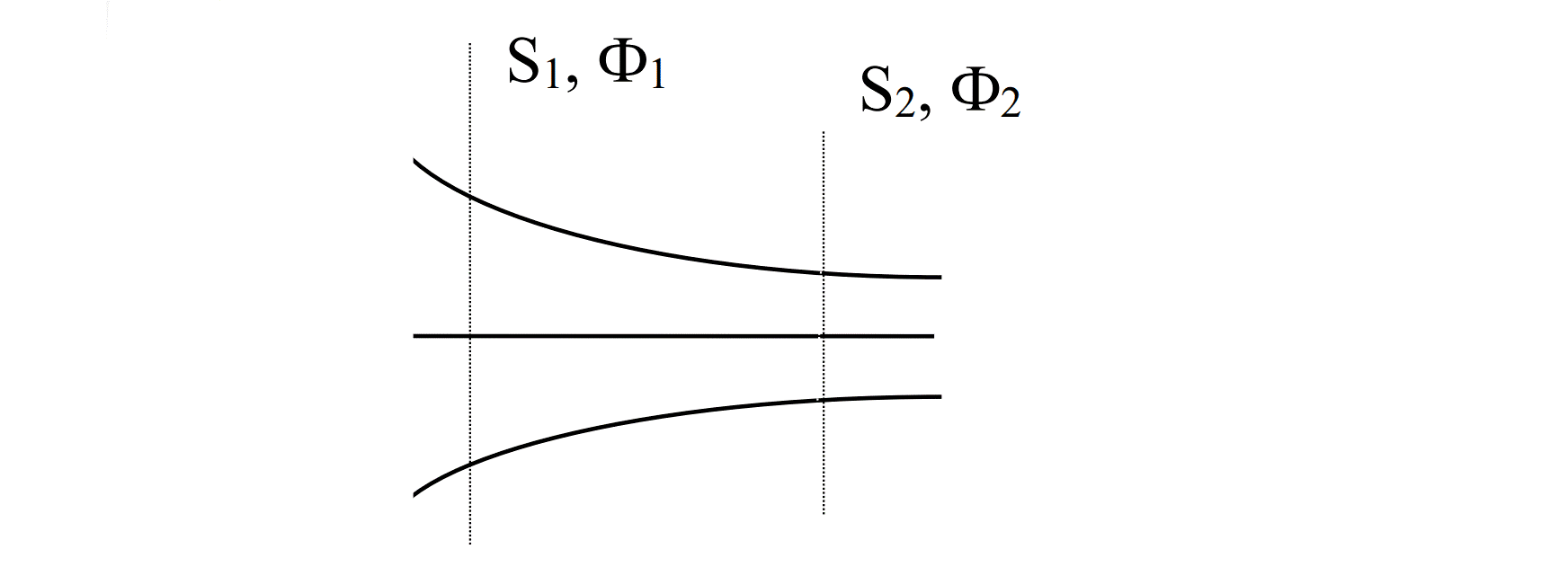
2] В узле (разветвлении) сердечника алгебраическая сумма потоков (с учетом их направлений) будет равна нулю... Мне одному это что-то напоминает?

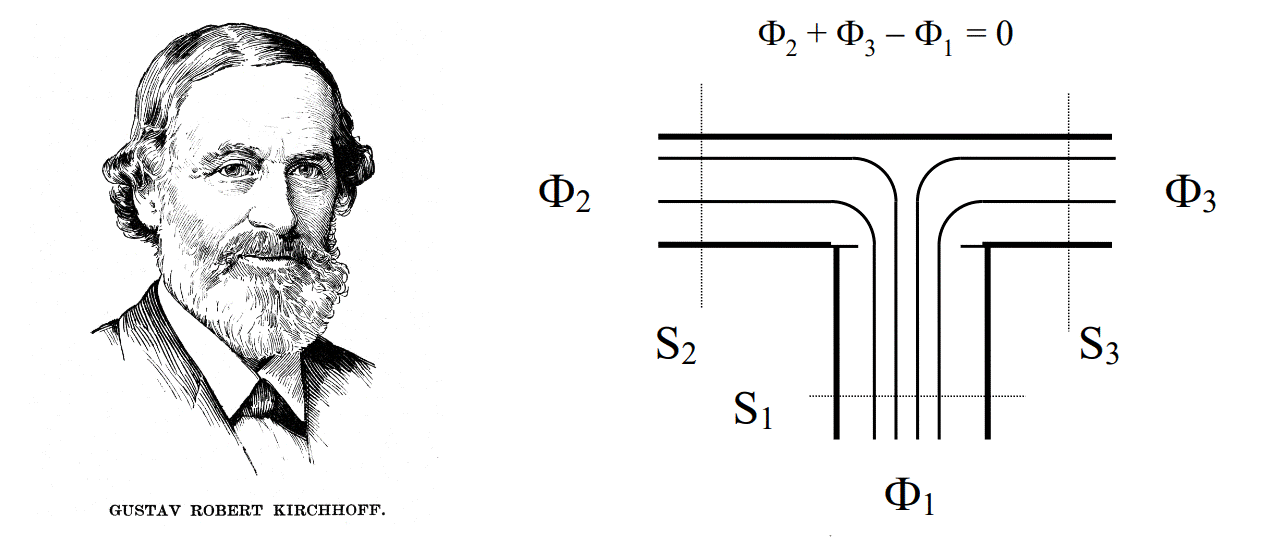
То есть мы окончательно сформулировали, что замкнутая (или почти замкнутая) система из ферромагнитных сердечников может рассматриваться как проводящая цепь. В нашем случае - магнитная.

Расчет магнитных цепей

Теперь внимание. Мы можем провести прямую аналогию и рассматривать магнитный поток в цепи, как характеристику электрической цепи - силу тока. Рассмотренное второе следствие означает, что для магнитной цепи, также как и для электрической, справедливо первое правило Кирхгофа. Отсюда можно лаконично перейти к закону полного тока, который в рамках классического магнетизма будет выглядеть следующим образом (приготовьтесь, немного математики):

Криволинейный интеграл по замкнутому контуру от напряженности магнитного поля будет равен алгебраической сумме токов, сцепленных (окруженных) данным контуром.

Также мы помним, что напряженность магнитного поля связана с магнитным потоком следующим образом:

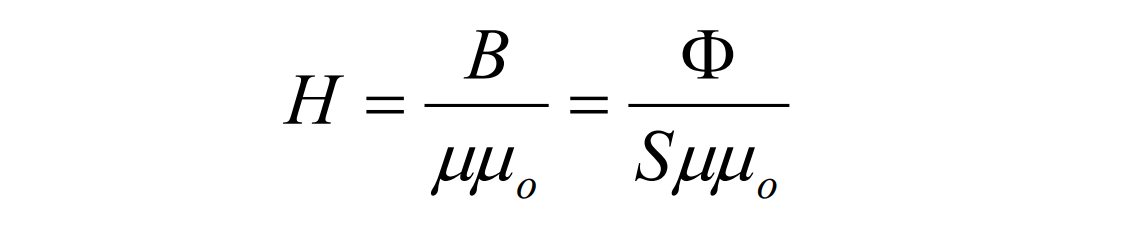
Руководствуясь приведенным законом полного тока и определением напряженности через магнитный поток, мы можем переписать закон полного тока относительно магнитного потока.

Откуда в уравнении появился и что символизирует аргумент l? Все просто. Так как мы рассматриваем контур L, то логично предположить, что на разных его участках наши показатели могут принимать разные значения: площадь сечения может изменяться, как и магнитная проницаемость или магнитный поток.

Полученное уравнение можно рассматривать как второй закон Кирхгофа, который, напомню, звучит следующим образом:

В любой момент времени алгебраическая сумма напряжений на ветвях контура равна нулю.

Для полной ясности, проведем аналогию между электрическими и магнитными цепями, а также их величинами.

Именно проведя аналогичное представление для электрической цепи, мы можем рассчитывать магнитные цепи. Для того, чтобы это сделать, следует:

• Мысленно разбить сердечник на отдельные однородные участки (непрерывные, с постоянным сечением) без разветвлений и определить их магнитные сопротивления;

• Построить эквивалентную электрическую цепь, последовательно заменяя участки магнитной цепи участками электрической с электрическими сопротивлениями, а также заменяя индуктивности (катушки) на источники ЭДС;

• После обозначения заданных сопротивлений и ЭДС, можем вычислить в общем токи в элементах электрической цепи;

• Произвести замену полученных величин согласно таблице (токи в потоки, ЭДС в МДС [Магнитодвижущую силу / Ампер-витки], а электрическое сопротивление в магнитное сопротивление).

Именно таким образом, мы можем рассчитать характеристики магнитной цепи. Полученные результаты позволяют, например, вычислить индуктивности.

А примеры расчетов будут?

Здесь - нет. А по ссылке - да! В данном документе Самарского государственного технического университета рассмотрены базовые примеры, которые позволят лучше разобраться в теме, если она вас заинтересовала. Помимо всего прочего, там же приведены теоретические справки. Советую прочитать в надежде, что вы сможете для себя что-то новое подчерпнуть.

Заключение

Во-первых, спасибо, что дочитали статью! Один из способов поддержать меня как автора - подписаться на мой паблик Вконтакте, где иногда выходят «локальные статьи».

Во-вторых, вернемся к началу статьи. Там я задался целью показать, почему физика удивительна. Не хочу быть многословным, поэтому просто попрошу вспомнить все то, что было описано выше. Мы оперировали моделями, которые относятся к разделу физики электричества и перенесли их на физику магнетизма. Наверняка, вы замечали, насколько часто встречаются элементы механики в иных разделах. Это по истине удивительно! Однако главное не поработиться иллюзией, что в мире все законы нам предельно известны...