Недавно я решил написать свою собственную реализацию длинной арифметики для C++. Делал просто для себя, ибо эта тема мне кажется довольно интересной. Поставил перед собой следующие задачи:
Реализация должна быть шустрой. Я, к сожалению, пока не обладаю знаниями высшей математики, но пользоваться интернетом умею и постарался интегрировать в программу все, что только смог найти.
Реализация должна быть экономна к памяти. Понятное дело, что многопоточность и алгоритмы умножения вроде Карацубы подъедают память, но все-таки должен быть разумный предел.
Код должен быть относительно чистым, а то, как пользоваться классом - должно быть понятно и похоже на способы работы с обычными int-овыми числами.
Код должен содержать необходимый набор функций, чтобы используя его можно было спокойно проводить проверки на простоту и выполнять некоторые другие необходимые и популярные операции.
Сразу предупрежу, что статья не претендует на звание лучшей реализации длинных чисел, но все-же будет полезна тем, кто еще не реализовывал что-либо подобное.
Реализовывать буду знаковую целочисленную арифметику. Запаситесь провизией, поскольку рассказ будет долгий.
Для начала нам надо определиться, из чего будет состоять будущий проект. Выглядеть все будет примерно вот так:
../examples/main.cpp (некий демонстрационный калькулятор, демонстрирующий функционал)
../src/LongInt.hpp (заголовок класса)
../src/Conversation.cpp (объекты класса, отвечающие за конвертацию типов)
../src/Compare.cpp (объекты класса, отвечающие за сравнение)
../src/Primitive.cpp (объекты класса, отвечающие за примитивные операции)
../src/Sum.cpp (объекты класса, отвечающие за сложение)
../src/Subtraction.cpp (объекты класса, отвечающие за вычитание)
../src/Multiply.cpp (объекты класса, отвечающие за умножение)
../src/Division.cpp (объекты класса, отвечающие за деление)
../src/Pow.cpp (объекты класса, отвечающие за возведение в степень)
../src/Factorial.cpp (объекты класса, отвечающие за подсчет факториала)
../src/Gcd.cpp (объекты класса, отвечающие за подсчет НОД)
../src/Lcm.cpp (объекты класса, отвечающие за подсчет НОК)
../src/Isqrt.cpp (объекты класса, отвечающие за извлечение целого квадратного корня)
../src/Icbrt.cpp (объекты класса, отвечающие за извлечение целого кубического корня)
../src/Random.cpp (объекты класса, отвечающие за генерацию длинных псевдослучайных чисел заданной длины)
../CMakeLists.txt (инструкции компиляции)Файл с инструкциями компиляции напишем сразу.
Во-первых, подключим потоки. Это понадобится, ибо некоторые попытки что-либо распараллелить тут будут задействованы.
Во-вторых, активируем флаг Werror дабы код был чище (флаг Werror отвечает за то, чтобы все предупреждения компилятора прерывали процесс компиляции, это помогает заранее устранять зоопарк в коде).
cmake_minimum_required(VERSION 3.20)
project(LongInt)
set(CMAKE_CXX_STANDARD 14)
add_executable(LongInt ../examples/main.cpp ../src/LongInt.hpp ../src/Conversation.cpp ../src/Compare.cpp ../src/Primitive.cpp ../src/Sum.cpp ../src/Subtraction.cpp ../src/Multiply.cpp ../src/Division.cpp ../src/Pow.cpp ../src/Factorial.cpp ../src/Gcd.cpp ../src/Lcm.cpp ../src/Isqrt.cpp ../src/Icbrt.cpp ../src/Random.cpp)
add_definitions(-Werror)
find_package(Threads REQUIRED)
target_link_libraries(LongInt Threads::Threads)Файл с демонстрационным калькулятором пока пропустим, ибо сначала надо реализовать сам класс.
Делаем файл с заголовком класса:
#include <iostream>
#include <vector>
class LongInt {
public:
LongInt();
LongInt(std::string string);
LongInt(signed int number);
LongInt(unsigned int number);
LongInt(signed long number);
LongInt(unsigned long number);
LongInt(signed long long number);
LongInt(unsigned long long number);
static std::string to_string(LongInt number);
friend std::ostream& operator <<(std::ostream& ostream, const LongInt& number);
friend bool operator ==(LongInt number_first, LongInt number_second);
friend bool operator !=(LongInt number_first, LongInt number_second);
friend bool operator >(LongInt number_first, LongInt number_second);
friend bool operator <(const LongInt& number_first, const LongInt& number_second);
friend bool operator >=(const LongInt& number_first, const LongInt& number_second);
friend bool operator <=(const LongInt& number_first, const LongInt& number_second);
static LongInt abs(LongInt number_first);
static bool even(LongInt number);
static bool odd(LongInt number);
static long long size(LongInt number);
static LongInt max(LongInt number_first, LongInt number_second);
static LongInt min(LongInt number_first, LongInt number_second);
friend LongInt operator +(LongInt number_first, LongInt number_second);
LongInt operator +=(LongInt number);
LongInt operator ++();
LongInt operator ++(int);
friend LongInt operator -(LongInt number_first, LongInt number_second);
LongInt operator -=(LongInt number);
LongInt operator --();
LongInt operator --(int);
friend LongInt operator *(const LongInt& number_first, const LongInt& number_second);
LongInt operator *=(const LongInt& number);
friend LongInt operator /(LongInt number_first, LongInt number_second);
LongInt operator /=(LongInt number);
friend LongInt operator %(LongInt number_first, LongInt number_second);
LongInt operator %=(LongInt number);
static LongInt pow(LongInt number_first, LongInt number_second);
static LongInt factorial(LongInt number);
static LongInt gcd(LongInt number_first, LongInt number_second);
static LongInt lcm(LongInt number_first, LongInt number_second);
static LongInt isqrt(const LongInt& number);
static LongInt icbrt(LongInt number);
static LongInt random(long long number_length);
private:
std::vector<int> _digits;
bool _sign;
static const int _base = 1000000000;
static const int _base_length = 9;
static const int _length_maximum_for_default_multiply = 256;
static std::vector<int> _string_convert_to_vector(const std::string& string);
static LongInt _zeroes_leading_remove(LongInt number);
static LongInt _shift_right(LongInt number, long long shift_power);
static LongInt _shift_left(LongInt number, long long shift_power);
static LongInt _multiply_karatsuba(LongInt number_first, LongInt number_second, bool iteration_thirst);
static LongInt _factorial_tree(LongInt number_first, const LongInt& number_second);
};Тут, надо обратить внимание на несколько моментов. Сами разряды числа будут храниться в векторе _digits с указанной системой счисления.
В переменной _sign будет храниться знак числа. True - если знак + (иными словами >= 0), false - если знак - (иными словами < 0).
В переменной _base будет храниться база текущего числа. Сейчас поясню, почему выбрана именно 10^9. Во-первых, база должна быть натуральной степенью десятки, чтобы можно было легко и быстро переводить числа из нашей системы счисления в привычную для людей систему счисления, то есть десятичную. Во-вторых, база должна быть меньше типа int, то есть быть меньше 2^31-1. Это связано не только с тем, что вектор у нас типа int, а еще с тем, что конвертируя строку в вектор будет использоваться функция std::stoi, но об этом позже. В-третьих, при возведении в квадрат база должна быть меньше 2^63-1, чтобы избежать переполнение при операциях вроде умножения. Под эти условия подходят только 9 систем счисления: по основанию 10^1, по основанию 10^2, по основанию 10^3, по основанию 10^4, по основанию 10^5, по основанию 10^6, по основанию 10^7, по основанию 10^8 и по основанию 10^9. Мы выбираем наибольшую, ибо так мы значительно сэкономим память и уменьшим количество операций.
В переменной _base_length будет храниться количество нулей в текущей базе. У нас выбрана система счисления по основанию миллиард, следовательно, количество нулей - 9. Эта константа нужна для конвертации между системами счисления.
В переменной _length_maximum_for_default_multiply будет храниться значение до которого используется стандартное умножение в столбик, а не более быстрый алгоритм Анатолия Алексеевича Карацубы, но к этому мы еще вернемся.
Теперь приступим к самой тяжелой части кода - написания самих исходников объектов класса. Для начала, напишем файл с исходниками конвертации типов.
#include "LongInt.hpp"
std::vector<int> LongInt::_string_convert_to_vector(const std::string& string) {
std::vector<int> result;
if (string.size() % _base_length == 0) {
result.resize(string.size() / _base_length);
}
else {
result.resize(string.size() / _base_length + 1);
}
for (long long string_position = string.size() - 1, result_position = result.size() - 1; string_position >= 0; string_position = string_position - _base_length, result_position = result_position - 1) {
if ((string_position + 1) - _base_length <= 0) {
result[result_position] = std::stoi(string.substr(0, string_position + 1));
}
else {
result[result_position] = std::stoi(string.substr(string_position - _base_length + 1, _base_length));
}
}
return result;
}
LongInt::LongInt() {
_digits.resize(1);
_sign = true;
}
LongInt::LongInt(std::string string) {
if (string.empty() or (string.size() == 1 and string[0] == '-')) {
throw "Fatal error. Cannot create type. String does not contain a number.";
}
if (string.front() == '-') {
string.erase(string.begin());
_sign = false;
}
else {
_sign = true;
}
for (long long i = 0; i < string.size(); i = i + 1) {
if (string[i] < 48 or string[i] > 57) {
throw "Fatal error. Cannot create type. String contains unknown characters.";
}
}
while (string.size() != 1 and string.front() == '0') {
string.erase(string.begin());
}
_digits = LongInt::_string_convert_to_vector(string);
}
LongInt::LongInt(signed int number) {
std::string string = std::to_string(number);
if (string.front() == '-') {
string.erase(string.begin());
_sign = false;
}
else {
_sign = true;
}
_digits = LongInt::_string_convert_to_vector(string);
}
LongInt::LongInt(unsigned int number) {
_sign = true;
_digits = LongInt::_string_convert_to_vector(std::to_string(number));
}
LongInt::LongInt(signed long number) {
std::string string = std::to_string(number);
if (string.front() == '-') {
string.erase(string.begin());
_sign = false;
}
else {
_sign = true;
}
_digits = LongInt::_string_convert_to_vector(string);
}
LongInt::LongInt(unsigned long number) {
_sign = true;
_digits = LongInt::_string_convert_to_vector(std::to_string(number));
}
LongInt::LongInt(signed long long number) {
std::string string = std::to_string(number);
if (string.front() == '-') {
string.erase(string.begin());
_sign = false;
}
else {
_sign = true;
}
_digits = LongInt::_string_convert_to_vector(string);
}
LongInt::LongInt(unsigned long long number) {
_sign = true;
_digits = LongInt::_string_convert_to_vector(std::to_string(number));
}
std::string LongInt::to_string(LongInt number) {
if (number._digits.size() == 1 and number._digits.front() == 0) {
return "0";
}
std::string result;
if (!number._sign) {
result.append("-");
}
result.reserve(number._digits.size() * (_base_length - 1));
std::string tmp;
result.append(std::to_string(number._digits[0]));
for (long long i = 1; i < number._digits.size(); i = i + 1) {
tmp = std::to_string(number._digits[i]);
tmp.reserve(_base_length - tmp.size());
while (tmp.size() < _base_length) {
tmp.insert(tmp.begin(), '0');
}
result.append(tmp);
}
return result;
}
std::ostream& operator <<(std::ostream& ostream, const LongInt& number) {
std::string string = LongInt::to_string(number);
for (long long i = 0; i < string.size(); i = i + 1) {
ostream.put(string[i]);
}
return ostream;
}Функция _string_convert_to_vector принимает натуральную строку без лидирующих нулей и без неизвестных символов и приводит ее к вектору базы, указанной в константе. Пустой конструктор просто кладет в вектор ноль и устанавливает в переменную _sign истинное значение. Конструктор из строки обрабатывает возможные исключения, после чего конвертирует отшлифованную строку в нужный нам вектор, а конструкторы из целочисленных типов вовсе пишутся элементарно.
Единственное, что важно подчеркнуть в конвертации в строку, что дополнение нулями до текущей базы не происходит на первом разряде числа. Как это объяснить - не знаю, но на опытах было выявленно, что дополнять нулями надо все разряды кроме первого.
Далее необходимо написать файл со сравнением. Основная идея сравнения. Сначала пытаемся определить какое число больше по знаку, потом - по разрядности, а уже потом если ничего из первых двух проверок не дало однозначного результата - проходим по разрядам. Полноценно реализовано будет только два оператора сравнения, остальные будут выведены на их основе.
#include <algorithm>
#include "LongInt.hpp"
bool operator ==(LongInt number_first, LongInt number_second) {
if (number_first._sign != number_second._sign) {
return false;
}
if (number_first._digits.size() != number_second._digits.size()) {
return false;
}
for (long long numbers_position = 0; numbers_position < number_first._digits.size(); numbers_position = numbers_position + 1) {
if (number_first._digits[numbers_position] != number_second._digits[numbers_position]) {
return false;
}
}
return true;
}
bool operator !=(LongInt number_first, LongInt number_second) {
return !(std::move(number_first) == std::move(number_second));
}
bool operator >(LongInt number_first, LongInt number_second) {
if (number_first == number_second) {
return false;
}
if (number_first._sign and !number_second._sign) {
return true;
}
if (!number_first._sign and number_second._sign) {
return false;
}
if (!number_first._sign and !number_second._sign) {
number_first._sign = true;
number_second._sign = true;
return !(number_first > number_second);
}
if (number_first._digits.size() > number_second._digits.size()) {
return true;
}
if (number_first._digits.size() < number_second._digits.size()) {
return false;
}
return !(std::lexicographical_compare(number_first._digits.begin(), number_first._digits.end(), number_second._digits.begin(), number_second._digits.end()));
}
bool operator <(const LongInt& number_first, const LongInt& number_second) {
if (number_first != number_second and !(number_first > number_second)) {
return true;
}
return false;
}
bool operator >=(const LongInt& number_first, const LongInt& number_second) {
if (number_first > number_second or number_first == number_second) {
return true;
}
return false;
}
bool operator <=(const LongInt& number_first, const LongInt& number_second) {
if (number_first < number_second or number_first == number_second) {
return true;
}
return false;
}Теперь напишем файл с примитивными функциями. Эти функции понадобятся при реализации более сложных операций. Функции очень простые и в пояснении, надеюсь, не нуждаются.
#include "LongInt.hpp"
LongInt LongInt::_zeroes_leading_remove(LongInt number) {
long long zeroes_leading_border = number._digits.size() - 1;
for (long long i = 0; i < number._digits.size() - 1; i = i + 1) {
if (number._digits[i] != 0) {
zeroes_leading_border = i;
break;
}
}
number._digits.erase(number._digits.begin(), number._digits.begin() + zeroes_leading_border);
return number;
}
LongInt LongInt::_shift_right(LongInt number, long long shift_power) {
number._digits.reserve(shift_power);
for (long long i = 0; i < shift_power; i = i + 1) {
number._digits.insert(number._digits.begin(), 0);
}
return number;
}
LongInt LongInt::_shift_left(LongInt number, long long shift_power) {
if (number == 0) {
return number;
}
number._digits.resize(number._digits.size() + shift_power);
return number;
}
LongInt LongInt::abs(LongInt number_first) {
number_first._sign = true;
return number_first;
}
bool LongInt::even(LongInt number) {
if (number._digits.back() % 2 == 0) {
return true;
}
return false;
}
bool LongInt::odd(LongInt number) {
return !LongInt::even(std::move(number));
}
long long LongInt::size(LongInt number) {
return (((long long)number._digits.size() - (long long)1) * (long long)_base_length) + (long long)std::to_string(number._digits.front()).size();
}
LongInt LongInt::max(LongInt number_first, LongInt number_second) {
if (number_first > number_second) {
return number_first;
}
return number_second;
}
LongInt LongInt::min(LongInt number_first, LongInt number_second) {
if (number_first < number_second) {
return number_first;
}
return number_second;
}Теперь напишем файл со сложением.
#include "LongInt.hpp"
LongInt operator +(LongInt number_first, LongInt number_second) {
if (number_first._sign and !number_second._sign) {
number_second._sign = true;
return number_first - number_second;
}
if (!number_first._sign and number_second._sign) {
number_first._sign = true;
return number_second - number_first;
}
if (!number_first._sign and !number_second._sign) {
number_second._sign = true;
}
if (number_first._digits.size() > number_second._digits.size()) {
number_second = LongInt::_shift_right(number_second, number_first._digits.size() - number_second._digits.size());
}
else {
number_first = LongInt::_shift_right(number_first, number_second._digits.size() - number_first._digits.size());
}
int sum;
int in_mind = 0;
for (long long numbers_position = number_first._digits.size() - 1; numbers_position >= 0; numbers_position = numbers_position - 1) {
sum = number_first._digits[numbers_position] + number_second._digits[numbers_position] + in_mind;
in_mind = sum / LongInt::_base;
number_first._digits[numbers_position] = sum % LongInt::_base;
}
if (in_mind != 0) {
number_first._digits.insert(number_first._digits.begin(), in_mind);
}
return number_first;
}
LongInt LongInt::operator +=(LongInt number) {
return *this = *this + std::move(number);
}
LongInt LongInt::operator ++() {
return *this = *this + 1;
}
LongInt LongInt::operator ++(int) {
*this = *this + 1;
return *this = *this - 1;
}Из-за большого количества сценариев, зависящих от знака входных чисел, пришлось писать много кода. Для сложения используется обычный алгоритм сложения в столбик, с которым все, смею предположить, знакомы.
Теперь время файла с вычитанием.
#include "LongInt.hpp"
LongInt operator -(LongInt number_first, LongInt number_second) {
if (number_first._sign and !number_second._sign) {
number_second._sign = true;
return number_first + number_second;
}
if (!number_first._sign and number_second._sign) {
number_first._sign = true;
LongInt tmp = number_first + number_second;
tmp._sign = false;
return tmp;
}
if (!number_first._sign and !number_second._sign) {
number_first._sign = true;
number_second._sign = true;
LongInt tmp;
tmp = number_first;
number_first = number_second;
number_second = tmp;
}
if (number_first < number_second) {
LongInt tmp = number_first;
number_first = number_second;
number_second = tmp;
number_first._sign = false;
}
number_second = LongInt::_shift_right(number_second, number_first._digits.size() - number_second._digits.size());
int different;
for (long long numbers_position1 = number_first._digits.size() - 1; numbers_position1 >= 0; numbers_position1 = numbers_position1 - 1) {
different = number_first._digits[numbers_position1] - number_second._digits[numbers_position1];
if (different >= 0) {
number_first._digits[numbers_position1] = different;
}
else {
number_first._digits[numbers_position1] = different + LongInt::_base;
for (long long numbers_position2 = numbers_position1 - 1; true; numbers_position2 = numbers_position2 - 1) {
if (number_first._digits[numbers_position2] == 0) {
number_first._digits[numbers_position2] = LongInt::_base - 1;
}
else {
number_first._digits[numbers_position2] = number_first._digits[numbers_position2] - 1;
break;
}
}
}
}
return LongInt::_zeroes_leading_remove(number_first);
}
LongInt LongInt::operator -=(LongInt number) {
return *this = *this - std::move(number);
}
LongInt LongInt::operator --() {
return *this = *this - 1;
}
LongInt LongInt::operator --(int) {
*this = *this - 1;
return *this = *this + 1;
}Вычитание работает немного труднее, но в целом это то же примитивное вычитание в столбик.
Теперь настало время одной из самых интересных частей статьи. А именно - умножения. Будет использоваться алгоритм Анатолия Алексеевича Карацубы (см. Алгоритм Карацубы). Это не очень сложный алгоритм, он основан на парадигме "разделяй и влавствуй". Обратите внимание, что из-за рекурсии алгоритм необходимо разделить на две части. Вот файл с умножением:
#include <future>
#include "LongInt.hpp"
LongInt LongInt::_multiply_karatsuba(LongInt number_first, LongInt number_second, bool iteration_thirst) {
if (std::min(number_first._digits.size(), number_second._digits.size()) <= _length_maximum_for_default_multiply) {
number_first = LongInt::_zeroes_leading_remove(number_first);
number_second = LongInt::_zeroes_leading_remove(number_second);
LongInt result;
result._digits.resize(number_first._digits.size() + number_second._digits.size());
long long composition;
for (long long number_first_position = number_first._digits.size() - 1; number_first_position >= 0; number_first_position = number_first_position - 1) {
for (long long number_second_position = number_second._digits.size() - 1; number_second_position >= 0; number_second_position = number_second_position - 1) {
composition = (long long)number_first._digits[number_first_position] * (long long)number_second._digits[number_second_position] + result._digits[number_first_position + number_second_position + 1];
result._digits[number_first_position + number_second_position + 1] = composition % LongInt::_base;
result._digits[number_first_position + number_second_position] = result._digits[number_first_position + number_second_position] + (composition / LongInt::_base);
}
}
return LongInt::_zeroes_leading_remove(result);
}
if (number_first._digits.size() % 2 != 0) {
number_first._digits.insert(number_first._digits.begin(), 0);
}
if (number_second._digits.size() % 2 != 0) {
number_second._digits.insert(number_second._digits.begin(), 0);
}
if (number_first._digits.size() > number_second._digits.size()) {
number_second = LongInt::_shift_right(number_second, number_first._digits.size() - number_second._digits.size());
}
else {
number_first = LongInt::_shift_right(number_first, number_second._digits.size() - number_first._digits.size());
}
long long numbers_size = number_first._digits.size();
long long numbers_part_size = numbers_size / 2;
LongInt number_first_part_left;
LongInt number_first_part_right;
LongInt number_second_part_left;
LongInt number_second_part_right;
number_first_part_left._digits.resize(numbers_part_size);
number_first_part_right._digits.resize(numbers_part_size);
number_second_part_left._digits.resize(numbers_part_size);
number_second_part_right._digits.resize(numbers_part_size);
std::copy(number_first._digits.begin(), number_first._digits.begin() + numbers_part_size, number_first_part_left._digits.begin());
std::copy(number_second._digits.begin(), number_second._digits.begin() + numbers_part_size, number_second_part_left._digits.begin());
std::copy(number_first._digits.begin() + numbers_part_size, number_first._digits.begin() + numbers_size, number_first_part_right._digits.begin());
std::copy(number_second._digits.begin() + numbers_part_size, number_second._digits.begin() + numbers_size, number_second_part_right._digits.begin());
LongInt product_first;
LongInt product_second;
LongInt product_third;
if (iteration_thirst and std::thread::hardware_concurrency() >= 3) {
auto thread_first = std::async(LongInt::_multiply_karatsuba, number_first_part_left, number_second_part_left, false);
auto thread_second = std::async(LongInt::_multiply_karatsuba, number_first_part_right, number_second_part_right, false);
product_third = LongInt::_multiply_karatsuba(LongInt::_zeroes_leading_remove(number_first_part_left) + LongInt::_zeroes_leading_remove(number_first_part_right), LongInt::_zeroes_leading_remove(number_second_part_left) + LongInt::_zeroes_leading_remove(number_second_part_right), false);
product_first = thread_first.get();
product_second = thread_second.get();
}
else if (iteration_thirst and std::thread::hardware_concurrency() == 2) {
auto thread_first = std::async(LongInt::_multiply_karatsuba, number_first_part_left, number_second_part_left, false);
product_second = LongInt::_multiply_karatsuba(number_first_part_right, number_second_part_right, false);
product_third = LongInt::_multiply_karatsuba(LongInt::_zeroes_leading_remove(number_first_part_left) + LongInt::_zeroes_leading_remove(number_first_part_right), LongInt::_zeroes_leading_remove(number_second_part_left) + LongInt::_zeroes_leading_remove(number_second_part_right), false);
product_first = thread_first.get();
}
else {
product_first = LongInt::_multiply_karatsuba(number_first_part_left, number_second_part_left, false);
product_second = LongInt::_multiply_karatsuba(number_first_part_right, number_second_part_right, false);
product_third = LongInt::_multiply_karatsuba(LongInt::_zeroes_leading_remove(number_first_part_left) + LongInt::_zeroes_leading_remove(number_first_part_right), LongInt::_zeroes_leading_remove(number_second_part_left) + LongInt::_zeroes_leading_remove(number_second_part_right), false);
}
return LongInt::_shift_left(product_first, numbers_size) + LongInt::_shift_left(product_third - (product_first + product_second), numbers_part_size) + product_second;
}
LongInt operator *(const LongInt& number_first, const LongInt& number_second) {
LongInt result = LongInt::_multiply_karatsuba(number_first, number_second, true);
result._sign = (number_first._sign == number_second._sign);
return result;
}
LongInt LongInt::operator *=(const LongInt& number) {
return *this = *this * number;
}Теперь предлагаю разобрать, что именно мы написали. После вызова оператора умножения мы сразу запускаем рекурсивный алгоритм, а после рекурсии определяем знак числа. Далее просто возвращаем результат. Но самое интересное в этом блоке кода именно рекурсивный алгоритм, перейдем к нему. Сразу после запуска функции мы проверяем минимальную длину входных чисел. Если она меньше или равна 256 (такое значение по умолчанию, на своем железе я протестировал и 256 оказалось оптимальным вариантом), то удаляем лидирующие нули (ибо такие могут быть и скоро вы поймете почему) и умножаем банально в столбик. Однако почему мы используем алгоритм умножения в столбик? А потому, что алгоритм Карацубы дает преимущество только на больших числах из-за лишних затрат на сложение, вычитание, сдвиги и так далее. Далее, если код продолжается, то очевидно, что числа здоровенные. Дополняем их длину до четной, после чего равняем. Нам это понадобится. Делим два числа на равные части (именно для этого нужны были дополнения нолями), после чего рекурсивно, согласно алгоритму Карацубы, перемножаем. Тут надо обратить внимание на один момент. Если это первый рекурсивный вызов, то рекурсивные умножения делаются не последовательно, а параллельно. Многопоточные вычисления накладывают дополнительные расходы, но возможность использовать три потока вместо одного эти расходы с лихвой компенсирует. Так же стоит заметить, что выполнение параллельных вычислений зависит от потоков CPU.
Далее у нас на очереди файл с делением. В файле будут находится сразу две крупных функции: деление нацело и получение остатка от деления. Для начала разберем деление нацело. Для деления на короткое число (меньше базы) существует относительно быстрый алгоритм, когда для деления на длинные числа (больше или равные базе) нормальных алгоритмом практически не существует. Поэтому, для деления на короткое число будет использоваться один алгоритм, а для деления на длинное - немного странный, но рабочий алгоритм деления уголком. Первый алгоритм прост до безобразия, а во втором единственное, что хочется отметить - что для нахождения "промежуточно делимого" будет использоваться бинарный поиск. Получение остатка от деления почти не отличается от деления нацело. Стоит заметить только то, что остаток от деления всегда больше или равен нулю.
#include "LongInt.hpp"
LongInt operator /(LongInt number_first, LongInt number_second) {
if (number_second == 0) {
throw "Fatal error. Whole division is not possible. Zero is specified as the divisor.";
}
if (number_second._digits.size() == 1) {
int number_second_integer = number_second._digits.front();
int in_mind = 0;
long long composition;
for (long long i = 0; i < number_first._digits.size(); i = i + 1) {
composition = (long long)number_first._digits[i] + (long long)in_mind * (long long)LongInt::_base;
number_first._digits[i] = composition / number_second_integer;
in_mind = composition % number_second_integer;
}
number_first._sign = (number_first._sign == number_second._sign);
return LongInt::_zeroes_leading_remove(number_first);
}
LongInt result;
result._sign = (number_first._sign == number_second._sign);
LongInt number_first_part;
number_first._sign = true;
number_second._sign = true;
if (number_first < number_second) {
return 0;
}
result._digits.resize(0);
number_first_part._digits.resize(0);
int quotient;
int left;
int middle;
int right;
LongInt tmp;
for (long long number_first_position = 0; number_first_position < number_first._digits.size(); number_first_position = number_first_position + 1) {
number_first_part._digits.push_back(number_first._digits[number_first_position]);
quotient = 0;
left = 0;
right = LongInt::_base;
while (left <= right) {
middle = (left + right) / 2;
tmp = number_second * middle;
if (tmp <= number_first_part) {
quotient = middle;
left = middle + 1;
}
else {
right = middle - 1;
}
}
number_first_part = number_first_part - (number_second * quotient);
if (!result._digits.empty() or quotient != 0) {
result._digits.push_back(quotient);
}
if (number_first_part == 0) {
number_first_part._digits.resize(0);
}
}
return result;
}
LongInt LongInt::operator /=(LongInt number) {
return *this = *this / std::move(number);
}
LongInt operator %(LongInt number_first, LongInt number_second) {
if (number_second == 0) {
throw "Fatal error. It is not possible to get the remainder of the division. Zero is specified as the divisor.";
}
if (number_second._digits.size() == 1) {
int number_second_integer = number_second._digits.front();
int in_mind = 0;
long long composition;
for (long long i = 0; i < number_first._digits.size(); i = i + 1) {
composition = (long long)number_first._digits[i] + (long long)in_mind * (long long)LongInt::_base;
number_first._digits[i] = composition / number_second_integer;
in_mind = composition % number_second_integer;
}
return in_mind;
}
LongInt number_first_part;
number_first._sign = true;
number_second._sign = true;
if (number_first < number_second) {
return number_first;
}
number_first_part._digits.resize(0);
int quotient;
int left;
int middle;
int right;
LongInt tmp;
for (long long number_first_position = 0; number_first_position < number_first._digits.size(); number_first_position = number_first_position + 1) {
number_first_part._digits.push_back(number_first._digits[number_first_position]);
quotient = 0;
left = 0;
right = LongInt::_base;
while (left <= right) {
middle = (left + right) / 2;
tmp = number_second * middle;
if (tmp <= number_first_part) {
quotient = middle;
left = middle + 1;
}
else {
right = middle - 1;
}
}
number_first_part = number_first_part - (number_second * quotient);
if (number_first_part == 0) {
number_first_part._digits.resize(0);
}
}
if (number_first_part._digits.empty()) {
return 0;
}
return number_first_part;
}
LongInt LongInt::operator %=(LongInt number) {
return *this = *this % std::move(number);
}Теперь на очереди более простые вещи. Файл с возведением в степень. Использываться будет один из алгоритмов быстрого возведения в степень. Алгоритм основан на том, что почти все умножения на основание степени можно заменить на возведение в квадрат. Рассмотрим этот вопрос чуть подробнее. Допустим нам надо возвести 2 в 13 степень. Бесппорно, по определению степени, для это достаточно выполнить следующие действия:
Мы обошлись 13 умножениями. Однако, возвести 2 в 13 степень можно всего за 5 операций умножения:
Бесспорно, операции умножения во втором способее тяжелее, но их становится куда меньше, что снижает время возведения в десятки, или даже сотни раз. Помимо этого стоит учитывать, что умножение приблизительно одинаковых чисел работает быстрее, чем умножение большого числа на маленькое, а тут мы как раз большую часть времени считаем квадраты чисел, а не умножаем разжиревшее число на двойки кучу раз, как это было бы с примитивным алгоритмом. Преимущество такого способа на 13 степени заметно не сильно, но если выполнить подобное преобразование, скажем, для тысячной степени, то преимущество будет заметно сразу. Обращаю внимание, что ноль нельзя возвести в нулевую степень.
#include "LongInt.hpp"
LongInt LongInt::pow(LongInt number_first, LongInt number_second) {
if (number_first == 0 and number_second == 0) {
throw "Fatal error. Exponentiation is not possible. Cannot raise zero to zero degree.";
}
if (number_second < 0) {
throw "Fatal error. Exponentiation is not possible. Specified number is less than zero.";
}
LongInt result = 1;
while (number_second != 0) {
if (even(number_second)) {
number_second = number_second / 2;
number_first = number_first * number_first;
}
else {
number_second = number_second - 1;
result = result * number_first;
}
}
return result;
}Теперь файл с функцией факториала. Казалось бы: все просто. Нужно только перемножить числа от 1 до n. Но все-таки не так все и просто. Дело в том, что просто перемножая числа от 1 до n мы будем работать с числами резко отличающейся длины, а это режет производительность. Поэтому, мы будем использовать алгоритм поиска факториала "деревом". Он основан на том, что мы добиваемся того, что умножаем числа всегда приблизительно равной длины. Статьи на Википедии или на каком-нибудь другом авторитетном источнике я не нашел, но для 10! это работает примерно так:
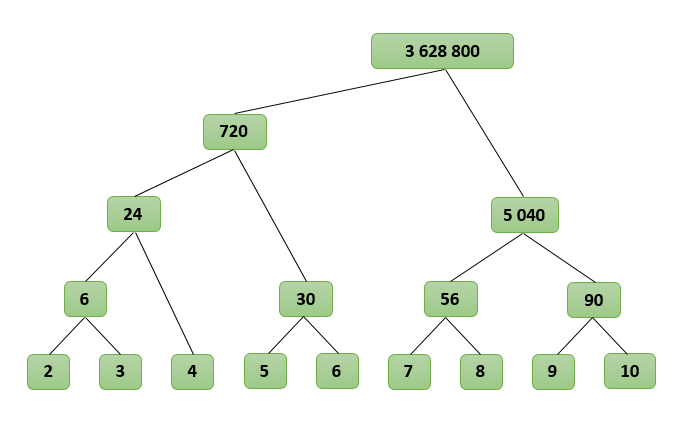
Теперь, реализация. Обратите внимание, что алгоритм разделен на две части из-за рекурсии, а также на то, что функция факториала определена только для натуральных чисел.
#include "LongInt.hpp"
LongInt LongInt::_factorial_tree(LongInt number_first, const LongInt& number_second) {
if (number_first > number_second) {
return 1;
}
if (number_first == number_second) {
return number_first;
}
if (number_second - number_first == 1) {
return number_first * number_second;
}
LongInt tmp = (number_first + number_second) / 2;
return LongInt::_factorial_tree(number_first, tmp) * LongInt::_factorial_tree(tmp + 1, number_second);
}
LongInt LongInt::factorial(LongInt number) {
if (number < 1) {
throw "Fatal error. The factorial calculation from the specified number is not possible. The specified number is less than or equal to zero.";
}
if (number == 1 or number == 2) {
return number;
}
return _factorial_tree(2, number);
}Далее у нас файл с функцией подсчета НОД. Использовать мы будем алгоритм Евклида (см. Алгоритм Евклида). Обратите внимание, что результат этой операции всегда натурален, а также, что нельзя подсчитать НОД если оба числа нули.
#include "LongInt.hpp"
LongInt LongInt::gcd(LongInt number_first, LongInt number_second) {
if (number_first == 0 and number_second == 0) {
throw "Fatal error. Counting the greatest common divisor is not possible. Both numbers are zero.";
}
number_first._sign = true;
number_second._sign = true;
if (number_first == 0) {
return number_second;
}
if (number_second == 0) {
return number_first;
}
while (number_first != 0 and number_second != 0) {
if (number_first > number_second) {
number_first = number_first % number_second;
}
else {
number_second = number_second % number_first;
}
}
return number_first + number_second;
}Далее файл с функцией подсчета НОК. Зная НОД числа найти НОК не составляет труда. Обратите внимание, что нельзя найти НОК если одно из чисел ноль, а также, что НОК всегда натурально.
#include "LongInt.hpp"
LongInt LongInt::lcm(LongInt number_first, LongInt number_second) {
if (number_first == 0 or number_second == 0) {
throw "Fatal error. Calculating the least common multiple is not possible. One of the numbers is zero.";
}
number_first._sign = true;
number_second._sign = true;
return number_first * number_second / LongInt::gcd(number_first, number_second);
}Теперь файл с функцией извлечения целого квадратного корня. Использоваться будет тот же бинарный поиск. Обратите внимание, что квадратного корня из отрицательного числа не существует.
#include "LongInt.hpp"
LongInt LongInt::isqrt(const LongInt& number) {
if (!number._sign) {
throw "Fatal error. Calculating an integer square root is not possible. The square root of the specified number does not exist.";
}
if (number == 0) {
return number;
}
LongInt left = 1;
LongInt right = number / 2 + 1;
LongInt middle;
LongInt result;
while (left <= right) {
middle = left + (right - left) / 2;
if (middle * middle <= number) {
left = middle + 1;
result = middle;
}
else {
right = middle - 1;
}
}
return result;
}Далее файл с функцией извлечения целого кубического корня. Целый кубический корень находит свое применение в ряде формлул, поэтому, его так же стоит написать. Извлечение целого кубического корня почти не отличается от извлечения целого квадратного корня, единственное, что стоит заметить, что кубический корень от отрицательного числа имеет решение, в отличие от квадратного.
#include "LongInt.hpp"
LongInt LongInt::icbrt(LongInt number) {
if (number == 0) {
return number;
}
bool result_natural = number._sign;
number._sign = true;
LongInt left = 1;
LongInt right = number / 2 + 1;
LongInt middle;
LongInt result;
while (left <= right) {
middle = left + (right - left) / 2;
if (middle * middle * middle <= number) {
left = middle + 1;
result = middle;
}
else {
right = middle - 1;
}
}
result._sign = result_natural;
return result;
}Теперь напишем файл с генератором псевдослучайных чисел заданной длины. Выглядеть это будет вот так:
#include <random>
#include <cmath>
#include "LongInt.hpp"
LongInt LongInt::random(long long number_length) {
if (number_length < 1) {
throw "Fatal error. Random number generation is not possible. Specified length is less than or equal to zero.";
}
LongInt result;
result._digits.resize(0);
std::random_device random_device;
std::mt19937 mersenne(random_device());
int tmp = 0;
if (number_length % _base_length == 0) {
while (tmp == 0 or std::to_string(tmp).size() != _base_length) {
tmp = mersenne() % _base;
}
result._digits.push_back(tmp);
number_length = number_length - _base_length;
}
else {
while (tmp == 0 or std::to_string(tmp).size() != number_length % _base_length) {
tmp = mersenne() % (unsigned int)std::pow(10, number_length % _base_length);
}
result._digits.push_back(tmp);
number_length = number_length - (number_length % _base_length);
}
result._digits.reserve(number_length / _base_length);
while (number_length != 0) {
result._digits.push_back(mersenne() % _base);
number_length = number_length - _base_length;
}
return result;
}На этом реализация функций подошла к концу, осталось лишь накидать демонстрационную программу и замерить производительность.
Вот файл демонстрационной программы. Ничего объяснять, думаю, тут не надо - программа элементарна.
#include <iostream>
#include <chrono>
#include "../src/LongInt.hpp"
int main() {
std::string number_first_string;
std::string number_second_string;
std::string action;
LongInt number_first;
LongInt number_second;
long double time_start;
long double time_end;
LongInt result_longint;
bool result_bool;
char result_char;
std::cout << "1| Сложение двух целых чисел." << std::endl;
std::cout << "2| Вычитание из целого числа целое число." << std::endl;
std::cout << "3| Умножение двух целых чисел." << std::endl;
std::cout << "4| Деление нацело двух целых чисел." << std::endl;
std::cout << "5| Получения остатка от деления двух целых чисел." << std::endl;
std::cout << "6| Возведение целого числа в целую неотрицательную степень." << std::endl;
std::cout << "7| Подсчет факториала от натурального числа." << std::endl;
std::cout << "8| Подсчет НОД двух целых чисел." << std::endl;
std::cout << "9| Подсчет НОК двух целых чисел." << std::endl;
std::cout << "10| Получение модуля целого числа." << std::endl;
std::cout << "11| Быстрая проверка целого числа на четность." << std::endl;
std::cout << "12| Быстрая проверка целого числа на нечетность." << std::endl;
std::cout << "13| Получение максимального из двух целых чисел." << std::endl;
std::cout << "14| Получение минимального из двух целых чисел." << std::endl;
std::cout << "15| Извлечение целого квадратного корня из целого неотрицательного числа." << std::endl;
std::cout << "16| Извлечение целого кубического корня из целого числа." << std::endl;
std::cout << "17| Генерация натурального псевдослучайного числа натуральной длины." << std::endl;
std::cout << "18| Получение количества десятичных разрядов в числе." << std::endl;
std::cout << "19| Выход." << std::endl;
for (; ;) {
std::cout << std::endl;
std::cout << std::endl;
std::cout << "Выберите операцию: ";
getline(std::cin, action);
if (action == "1") {
std::cout << "Введите первое число: ";
getline(std::cin, number_first_string);
std::cout << "Введите второе число: ";
getline(std::cin, number_second_string);
time_start = std::chrono::high_resolution_clock::now().time_since_epoch().count();
number_first = number_first_string;
number_second = number_second_string;
result_longint = number_first + number_second;
std::cout << "Результат: " << result_longint << "." << std::endl;
time_end = std::chrono::high_resolution_clock::now().time_since_epoch().count();
std::cout << "Затрачено времени [с учетом затрат на конвертацию типов и вывод]: " << (time_end - time_start) / 1000000000 << " секунд(а/ы)." << std::endl;
}
else if (action == "2") {
std::cout << "Введите первое число: ";
getline(std::cin, number_first_string);
std::cout << "Введите второе число: ";
getline(std::cin, number_second_string);
time_start = std::chrono::high_resolution_clock::now().time_since_epoch().count();
number_first = number_first_string;
number_second = number_second_string;
result_longint = number_first - number_second;
std::cout << "Результат: " << result_longint << "." << std::endl;
time_end = std::chrono::high_resolution_clock::now().time_since_epoch().count();
std::cout << "Затрачено времени [с учетом затрат на конвертацию типов и вывод]: " << (time_end - time_start) / 1000000000 << " секунд(а/ы)." << std::endl;
}
else if (action == "3") {
std::cout << "Введите первое число: ";
getline(std::cin, number_first_string);
std::cout << "Введите второе число: ";
getline(std::cin, number_second_string);
time_start = std::chrono::high_resolution_clock::now().time_since_epoch().count();
number_first = number_first_string;
number_second = number_second_string;
result_longint = number_first * number_second;
std::cout << "Результат: " << result_longint << "." << std::endl;
time_end = std::chrono::high_resolution_clock::now().time_since_epoch().count();
std::cout << "Затрачено времени [с учетом затрат на конвертацию типов и вывод]: " << (time_end - time_start) / 1000000000 << " секунд(а/ы)." << std::endl;
}
else if (action == "4") {
std::cout << "Введите первое число: ";
getline(std::cin, number_first_string);
std::cout << "Введите второе число: ";
getline(std::cin, number_second_string);
time_start = std::chrono::high_resolution_clock::now().time_since_epoch().count();
number_first = number_first_string;
number_second = number_second_string;
result_longint = number_first / number_second;
std::cout << "Результат: " << result_longint << "." << std::endl;
time_end = std::chrono::high_resolution_clock::now().time_since_epoch().count();
std::cout << "Затрачено времени [с учетом затрат на конвертацию типов и вывод]: " << (time_end - time_start) / 1000000000 << " секунд(а/ы)." << std::endl;
}
else if (action == "5") {
std::cout << "Введите первое число: ";
getline(std::cin, number_first_string);
std::cout << "Введите второе число: ";
getline(std::cin, number_second_string);
time_start = std::chrono::high_resolution_clock::now().time_since_epoch().count();
number_first = number_first_string;
number_second = number_second_string;
result_longint = number_first % number_second;
std::cout << "Результат: " << result_longint << "." << std::endl;
time_end = std::chrono::high_resolution_clock::now().time_since_epoch().count();
std::cout << "Затрачено времени [с учетом затрат на конвертацию типов и вывод]: " << (time_end - time_start) / 1000000000 << " секунд(а/ы)." << std::endl;
}
else if (action == "6") {
std::cout << "Введите первое число: ";
getline(std::cin, number_first_string);
std::cout << "Введите второе число: ";
getline(std::cin, number_second_string);
time_start = std::chrono::high_resolution_clock::now().time_since_epoch().count();
number_first = number_first_string;
number_second = number_second_string;
result_longint = LongInt::pow(number_first, number_second);
std::cout << "Результат: " << result_longint << "." << std::endl;
time_end = std::chrono::high_resolution_clock::now().time_since_epoch().count();
std::cout << "Затрачено времени [с учетом затрат на конвертацию типов и вывод]: " << (time_end - time_start) / 1000000000 << " секунд(а/ы)." << std::endl;
}
else if (action == "7") {
std::cout << "Введите число: ";
getline(std::cin, number_first_string);
time_start = std::chrono::high_resolution_clock::now().time_since_epoch().count();
number_first = number_first_string;
result_longint = LongInt::factorial(number_first);
std::cout << "Результат: " << result_longint << "." << std::endl;
time_end = std::chrono::high_resolution_clock::now().time_since_epoch().count();
std::cout << "Затрачено времени [с учетом затрат на конвертацию типов и вывод]: " << (time_end - time_start) / 1000000000 << " секунд(а/ы)." << std::endl;
}
else if (action == "8") {
std::cout << "Введите первое число: ";
getline(std::cin, number_first_string);
std::cout << "Введите второе число: ";
getline(std::cin, number_second_string);
time_start = std::chrono::high_resolution_clock::now().time_since_epoch().count();
number_first = number_first_string;
number_second = number_second_string;
result_longint = LongInt::gcd(number_first, number_second);
std::cout << "Результат: " << result_longint << "." << std::endl;
time_end = std::chrono::high_resolution_clock::now().time_since_epoch().count();
std::cout << "Затрачено времени [с учетом затрат на конвертацию типов и вывод]: " << (time_end - time_start) / 1000000000 << " секунд(а/ы)." << std::endl;
}
else if (action == "9") {
std::cout << "Введите первое число: ";
getline(std::cin, number_first_string);
std::cout << "Введите второе число: ";
getline(std::cin, number_second_string);
time_start = std::chrono::high_resolution_clock::now().time_since_epoch().count();
number_first = number_first_string;
number_second = number_second_string;
result_longint = LongInt::lcm(number_first, number_second);
std::cout << "Результат: " << result_longint << "." << std::endl;
time_end = std::chrono::high_resolution_clock::now().time_since_epoch().count();
std::cout << "Затрачено времени [с учетом затрат на конвертацию типов и вывод]: " << (time_end - time_start) / 1000000000 << " секунд(а/ы)." << std::endl;
}
else if (action == "10") {
std::cout << "Введите число: ";
getline(std::cin, number_first_string);
time_start = std::chrono::high_resolution_clock::now().time_since_epoch().count();
number_first = number_first_string;
result_longint = LongInt::abs(number_first);
std::cout << "Результат: " << result_longint << "." << std::endl;
time_end = std::chrono::high_resolution_clock::now().time_since_epoch().count();
std::cout << "Затрачено времени [с учетом затрат на конвертацию типов и вывод]: " << (time_end - time_start) / 1000000000 << " секунд(а/ы)." << std::endl;
}
else if (action == "11") {
std::cout << "Введите число: ";
getline(std::cin, number_first_string);
time_start = std::chrono::high_resolution_clock::now().time_since_epoch().count();
number_first = number_first_string;
result_bool = LongInt::even(number_first);
std::cout << "Результат: " << result_bool << "." << std::endl;
time_end = std::chrono::high_resolution_clock::now().time_since_epoch().count();
std::cout << "Затрачено времени [с учетом затрат на конвертацию типов и вывод]: " << (time_end - time_start) / 1000000000 << " секунд(а/ы)." << std::endl;
}
else if (action == "12") {
std::cout << "Введите число: ";
getline(std::cin, number_first_string);
time_start = std::chrono::high_resolution_clock::now().time_since_epoch().count();
number_first = number_first_string;
result_bool = LongInt::odd(number_first);
std::cout << "Результат: " << result_bool << "." << std::endl;
time_end = std::chrono::high_resolution_clock::now().time_since_epoch().count();
std::cout << "Затрачено времени [с учетом затрат на конвертацию типов и вывод]: " << (time_end - time_start) / 1000000000 << " секунд(а/ы)." << std::endl;
}
else if (action == "13") {
std::cout << "Введите первое число: ";
getline(std::cin, number_first_string);
std::cout << "Введите второе число: ";
getline(std::cin, number_second_string);
time_start = std::chrono::high_resolution_clock::now().time_since_epoch().count();
number_first = number_first_string;
number_second = number_second_string;
result_longint = LongInt::max(number_first, number_second);
std::cout << "Результат: " << result_longint << "." << std::endl;
time_end = std::chrono::high_resolution_clock::now().time_since_epoch().count();
std::cout << "Затрачено времени [с учетом затрат на конвертацию типов и вывод]: " << (time_end - time_start) / 1000000000 << " секунд(а/ы)." << std::endl;
}
else if (action == "14") {
std::cout << "Введите первое число: ";
getline(std::cin, number_first_string);
std::cout << "Введите второе число: ";
getline(std::cin, number_second_string);
time_start = std::chrono::high_resolution_clock::now().time_since_epoch().count();
number_first = number_first_string;
number_second = number_second_string;
result_longint = LongInt::min(number_first, number_second);
std::cout << "Результат: " << result_longint << "." << std::endl;
time_end = std::chrono::high_resolution_clock::now().time_since_epoch().count();
std::cout << "Затрачено времени [с учетом затрат на конвертацию типов и вывод]: " << (time_end - time_start) / 1000000000 << " секунд(а/ы)." << std::endl;
}
else if (action == "15") {
std::cout << "Введите число: ";
getline(std::cin, number_first_string);
time_start = std::chrono::high_resolution_clock::now().time_since_epoch().count();
number_first = number_first_string;
result_longint = LongInt::isqrt(number_first);
std::cout << "Результат: " << result_longint << "." << std::endl;
time_end = std::chrono::high_resolution_clock::now().time_since_epoch().count();
std::cout << "Затрачено времени [с учетом затрат на конвертацию типов и вывод]: " << (time_end - time_start) / 1000000000 << " секунд(а/ы)." << std::endl;
}
else if (action == "16") {
std::cout << "Введите число: ";
getline(std::cin, number_first_string);
time_start = std::chrono::high_resolution_clock::now().time_since_epoch().count();
number_first = number_first_string;
result_longint = LongInt::icbrt(number_first);
std::cout << "Результат: " << result_longint << "." << std::endl;
time_end = std::chrono::high_resolution_clock::now().time_since_epoch().count();
std::cout << "Затрачено времени [с учетом затрат на конвертацию типов и вывод]: " << (time_end - time_start) / 1000000000 << " секунд(а/ы)." << std::endl;
}
else if (action == "17") {
std::cout << "Введите число [оно должно помещаться в стандартные целочисленные типы]: ";
getline(std::cin, number_first_string);
time_start = std::chrono::high_resolution_clock::now().time_since_epoch().count();
result_longint = LongInt::random(std::stoi(number_first_string));
std::cout << "Результат: " << result_longint << "." << std::endl;
time_end = std::chrono::high_resolution_clock::now().time_since_epoch().count();
std::cout << "Затрачено времени [с учетом затрат на конвертацию типов и вывод]: " << (time_end - time_start) / 1000000000 << " секунд(а/ы)." << std::endl;
}
else if (action == "18") {
std::cout << "Введите число: ";
getline(std::cin, number_first_string);
time_start = std::chrono::high_resolution_clock::now().time_since_epoch().count();
number_first = number_first_string;
std::cout << "Результат: " << LongInt::size(number_first) << "." << std::endl;
time_end = std::chrono::high_resolution_clock::now().time_since_epoch().count();
std::cout << "Затрачено времени [с учетом затрат на конвертацию типов и вывод]: " << (time_end - time_start) / 1000000000 << " секунд(а/ы)." << std::endl;
}
else if (action == "19") {
break;
}
else {
std::cout << "Неизвестный номер команды. Введите число от 1 до 19." << std::endl;
}
}
return 0;
}Все файлы готовы - теперь можно со спокойной душой компилировать. Компилируется на моем ноутбуке довольно шустро - пару секунд. Теперь, предлагаю замерить время выполнения самых "долгих" операций и сравнить ее с временем выполнения, скажем, в Python 3.9, где реализация длинных чисел уже выполнена из коробки. Обращаю внимание, что тесты производятся с учетом затрат на конвертацию типов и печать в консоль. Тесты будут проводиться на моем ноутбуке, вот информация о системе:
Операционная система |
Debian GNU/Linux 11 Bullseye |
Компилятор |
gcc 10.2.1 |
Процессор |
Intel Core i5-8250U |
Оперативная память |
8GB |
А вот сами тесты производительности:
Название операции |
Время выполнения в Python 3.9 (в сек.) |
Время выполнения в данной реализации (в сек.) |
Возведение 2 в 1 000 000 степень (в Python 3.9 используется оператор "**", в данной реализации - функция LongInt::pow()) |
1.22 |
0.62 |
Возведение 2 в 10 000 000 степень (в Python 3.9 используется оператор "**", в данной реализации - функция LongInt::pow()) |
121.81 |
58.66 |
Подсчет факториала от 100 000 (в Python 3.9 используется функция math.factorial(), в данной реализации - LongInt::factorial()) |
2.91 |
2.79 |
Подсчет факториала от 1 000 000 (в Python 3.9 используется функция math.factorial(), в данной реализации - LongInt::factorial()) |
421.93 |
184.81 |
Исходя из тестов видно, что Python проигрывает в скорости все сильнее и сильнее с ростом сложности задачи, но справедливости ради стоит заметить, что тест этих двух функций затрагивает далеко не весь функционал реализаций.
Спасибо за чтение. Библиотека доступна в репозитории на Github.
P.S. Статья была в последний раз отредактирована 9 октября 2021 года.
Комментарии (68)

netch80
18.09.2021 18:33+3> Хоть и по математическим правилам ноль — не является натуральным числом, в этой реализации ноль будет рассматриваться как натуральное число, просто потому что так удобнее.
В советской традиции, да, 0 не натуральное. В американской, для сравнения, 0 входит в натуральные, а положительные у них ????⁺. Не знаю про другие страны посредине ;)
Иногда это обозначают ????⁺ и ????₀.
> Будет использоваться алгоритм Анатолия Алексеевича Карацубы. Это не сложный алгоритм, он основан на парадигме «разделяй и влавствуй».
Один коллега писал, что алгоритм Фюрера получился очень легко. Я не пробовал, но можно сравнить.
> В этом алгоритме ничего примечательного нет, стандартное деление уголком.
Вот тут можно было как раз сэкономить по максимуму через промежуточный делитель и предвычисление обратного множителя. В «Hackersʼ delight» описано в подробностях.
> LongInt operator /(LongInt number_thirst, LongInt number_second) {
Почти мелочь, но точно thirst — то есть «жажда»? Я ожидал first.
> Единственное, что стоит заметить, так это то, что остаток, согласно математическим правилам всегда натурален.
Термин для такого — E-деление (евклидово). Ссылка.
В общем, конечно, «ещё одна 100500-я реализация», но выглядит корректно.
Дополнительно замечу, что для целых десятичная арифметика обычно не используется, потому что эффективность «так себе». А вот для плавающей точки десятичная реализация имеет супер-смысл там в финансово-экономических расчётах. Но там ещё надо тщательно следить за точностью в цифрах после запятой.
gth-other Автор
18.09.2021 19:31Спасибо за комментарий! Учел и некоторые незначительные моменты (вроде "thirst" вместо "first" (-: ) исправил.

uncle_goga
18.09.2021 18:56+6Я извиняюсь, но что этот пост делает на хабре? Подобные изыскания проживают на geeksforgeeks и тому подобных сайтах. Очень здорово, что вы познаете C++, но задание не является чем-то сверхсложным или необычным, длинную арифметику реализуют все студенты к концу первого курса.

gth-other Автор
18.09.2021 19:35+2Понимаю, что задача не сверхсложная, но все-таки попытаюсь объяснить причину публикации именно на Хабре. Прошерстив русскоязычный интернет мне не удалось найти нормально описанных библиотек длинных чисел с реализациями быстрых алгоритмов и хоть немного насыщенным набором функций, так что материал, смею предположить, по-своему уникальный.
P.S. Под "мне не удалось найти нормально описанных библиотек длинных чисел с реализациями быстрых алгоритмов и хоть немного насыщенным набором функций", естественно, имеется ввиду не удалось найти среди доступно описанных библиотек на русском языке.

arax
18.09.2021 20:34+1Пример библиотеки, где это реализовано на профессиональном уровне: https://www.cryptopp.com/

gth-other Автор
18.09.2021 20:38+3Библиотек для работы с длинными числами очень много. Можно привести в пример тот же GMP. Но я уточнил, что имею ввиду именно доступно объясненные библиотеки на русском языке. Далеко не всякий человек может и хочет читать сухой английский в файлах с кодом, а статья с форматированием на Хабре - довольно доступный и легкий способ получения информации.

lz961
18.09.2021 19:42+18Быть может помогает Хабру остаться Хабром, а не сборником переводной публицистики.

KvanTTT
19.09.2021 13:31+6А что, на хабр нужно обязательно публиковать что-то сверхсложное или необычное? Автор написал про свой опыт, в комментах получил ценное ревью, набрался опыта в написании кода и статей. В следующий раз статья от него будет лучше, со временем будет приближаться к профессиональным.

SinsI
18.09.2021 20:05+7Прежде всего, такие библиотеки надо начинать писать с unit тестов - потому что гарантированно будет куча труднонаходимых ошибок.
Вместо зоопарка операторов сравнения - лучше использовать operator <=>, современные стандарты очень упрощают жизнь.
Конструкторы из int - лишние, достаточно самого большого типа long long.

gth-other Автор
18.09.2021 20:19+1Спасибо за комментарий!
Про необходимость тестирования - полностью согласен. Жаль, что писал код без чего-то подобного. Но все-таки я потратил довольно много времени на ручное тестирование, рассматривая все проблемные варианты, что пришли в голову, а также сверяя результаты сложных операций с результатами аналогичных операций с другими материалами, где уже реализованы длинные числа.
Про оператор <=> - изучу. Не знал о такой возможности.
Про возможность минимизировать количество конструкторов тоже не знал. Попробую что-нибудь подобное.

mapron
18.09.2021 20:47+2Дополню про сравнения — вместо сравнения массивов данных ручками есть std::lexicographical_compare.

gth-other Автор
18.09.2021 21:09-2Спасибо за комментарий, действительное неплохая идея, но все-таки это требует добавления заголовка с алгоритмами, а это немного увеличивает вес бинарника, блокирует использование подобного класса во многих олимпиадах по программированию и не дает такого понимания, какое дает ручное сравнение векторов. Помимо этого, вряд-ли использование функции лексикографического сравнения даст прирост производительности, ведь за ней стоит примерно тоже, что и написало в этой реализации.

mapron
18.09.2021 21:12+3добавления заголовка с алгоритмами, а это немного увеличивает вес бинарника
вы похоже плохо знакомы с C++блокирует использование подобного класса во многих олимпиадах по программированию
а где было в посте что-то про олимпиады? олимпиадное программирование это «ненормальное» программирование, в том плание что его правила никак нельзя применять к здоровому обучению хорошим практикам. А современное их состояние — использовать алгоритмы так где они дают более чистый и лаконичный код.
gth-other Автор
18.09.2021 21:24-1Вы несомненно правы и, вероятно, куда больше знаете о C++, нежели я (ни в коем случае не сарказм), но все-таки основная задача этой статьи показать людям что примерно находится под капотом библиотек для длинных чисел, а не создать что-то совершенное, поэтому, ручное сравнение мне кажется более логичным в рамках этой статьи.

mapron
18.09.2021 23:24+1Хорошо, я вашу позицию, намерения и способ их реализации теперь понял. Хочу сказать что со способом донесения до читателей (раз вы делаете образовательный контент) в принципе не согласен.
Я бы если бы делал тоже самое, постарался бы объяснить базовые операции, а не вываливал код циклов (т.е. даже в принципе не приводил бы этот код).
Но мы тут в этом не сойдемся, боюсь.
Спасибо в любом случае за труд; но постарайтесь сами тоже после написанного критично оценить результаты (не сейчас, может быть позже).

mapron
18.09.2021 20:49+2Ну и неконстантный рекурсивный оператор сравнения это уже г-код, извините.

gth-other Автор
18.09.2021 21:11+1Может и так, спорить не могу. Не являюсь экспертом в написании чистого кода, хоть и изо всех сил стараюсь.

vanxant
19.09.2021 12:14+2mapron имеет в виду, что вместо
friend bool operator ==(LongInt number_first, LongInt number_second);
должно бытьfriend bool operator ==(const LongInt& number_first, const LongInt& number_second);
ну, или для функции-членаbool operator ==(const LongInt& number_second) const;
const — потому что вы не меняете аргументы, а без указания const вы не сможете принимать, ну, константы.
ссылки — чтобы не копировать вектора, ибо зачем?
mapron
19.09.2021 12:17Вам сейчас ответят что это все для новичков С++, чтобы они суть поняли, зачем им все эти ссылки да константы. У автора одна шарманка на все советы)

gth-other Автор
19.09.2021 12:26Почему же на все советы? Действительно, так будет лучше, не заметил. Просто сначала не понял о чем речь.

DistortNeo
18.09.2021 20:36Я не совсем специалист по C++, но зачем операторы определять как friend?

gth-other Автор
18.09.2021 20:43+1Объект помеченный как "friend", то есть дружественный, в отличии от объекта не отмеченного как "friend" имеет доступ к приватной части класса. В данном случае, нам нужен доступ к приватной части класса ради доступа к знаку числа и вектору разрядов.

DistortNeo
18.09.2021 22:12+3А зачем так извращаться, если можно просто объявить оператор как член класса?
Единственное исключение — этоstd::ostream& operator <<(std::ostream& ostream, const LongInt& number), но в нём вы не используете доступ к приватным полям.
P.S. Вам бы получше с C++ разобраться: в половине случаев у вас передача аргумента идёт по значению. Зачем?

kovserg
18.09.2021 23:11+1Код должен содержать необходимый набор функций, чтобы используя его можно было спокойно проводить проверки на простоту и выполнять некоторые другие необходимые и популярные операции
И где этот необходимый набор? Как вы имеющимся классом на простоту проверять собираетесь? Обычно a^(p-1) % p используют для проверок где p-как раз то самое число что проверяют.
ps: Какие операции популярны в 2021?
gth-other Автор
18.09.2021 23:22+1Спасибо за комментарий!
Проверять числа на простоту собираюсь самым простейшим способом - перебором всех (или не всех, есть много несложных способов исключить ненужные делители) делителей до sqrt(n) + 1.
Под "популярным операциями" может выразился не слишком корректно. Я имел ввиду, чтобы с классом можно было работать почти так же комфортно, как и со стандартным типом int. То есть чтобы можно было одной строчкой возводить в степень, считать факториал, считать корень, считать НОД и НОК (на случай, если программисту вдруг понадобится сделать обыкновенные дроби), получать максимальное / минимальное из двух чисел (а не писать блок условий на 5 строк) и так далее.

BVN2
19.09.2021 00:32+2Самое плохое для автора - когда читатель-комментатор, видя малёхонький косяк, задаёт вопрос автору и получая естественный ответ, начинает умничать. По итогу демотивированный автор навсегда покидает поле.
Автор молодец! Не пожалел времени на реализацию и написание статьи. Всяко лучше, чем переводной науч-поп. По коду тоже всё норм. Код можно улучшать бесконечно и всё-равно найдётся какой-нибудь ворчун
Ritan
19.09.2021 06:16+3Если здесь по коду все норм, то теперь понятно почему любого вменяемого плюсовика пытаются схантить каждые несколько часов.
Здесь творится такой мрак, что спасает его только то, что компилятор смог его оптимизировать из-за расположения всего и вся в одном файле

BVN2
19.09.2021 11:19+2Здесь творится не мрак, здесь видно, что есть пробелы. Если автору будет интересна тема, то со временем он сам всё поправит и порадует новыми статьями с более высоким уровнем владения плюсов. Хз кого там хантят, но если человек не понимает очевидную психологию, то с ним трудно работать из-за отравления среды
Для автора: если тебе интересна математическая тема, тот вот тут https://leetcode.com/problemset/all/ есть интересные задачки

Woodroof
19.09.2021 07:34На основе int64_t работало бы быстрее. А то и на основе __int128, если он доступен.
Ну и заявляется быстрота, но нет сравнения хотя бы с тем же multiprecision.
Пока не перешли на модули, работу со строками, а тем более с потоками лучше было вынести в отдельный заголовочный файл, iostream — тяжёлый для компиляции. Иначе если у вас тип используется а большой части проекта, это будет заметно.

gth-other Автор
19.09.2021 09:26+1Спасибо за комментарий!
Немного не понял, что значит "на основе int64_t работало бы быстрее". Имеется ввиду, вектор стоит делать из 64-битного типа данных и, соответственно, увеличить базу? Но как тогда выполнять, скажем, умножение в столбик? В каком типе переменной хранить результат умножения?

Woodroof
19.09.2021 10:03Конкретно для умножения можно оперировать половинами, через >>32 и 0xffffffff.

vanxant
19.09.2021 12:05-2На основе int64_t работало бы быстрее
Не факт, ой не факт. Если сами вычисления не очень тяжелые, но нужно много выводить результаты, то int64_t повесится на этой операции (вам придется делать % 10 для каждой выводимой десятичной цифры). А у автора как раз всё отлично.
Woodroof
19.09.2021 16:55Да ну? И чем же перевод в десятичную форму N uint64_t (давайте про беззнаковые, чтобы не усложнять всё) тяжелее, чем N*2 uint32_t? Ровно то же число операций.
Не говоря уже о том, что вычисления всё-таки для таких типов - более частый кейс, чем вывод. А в вырожденных случаях можно и кэшировать.

vanxant
19.09.2021 17:23Тем, что здесь каждые 9 цифр независимы. Нужно 2*9*N 32-битных операций всего. Для вашего варианта с лонгами нужно для каждой цифры:
1. Взять остаток от деления длинного числа на 10 (это N * N / 2 операций, упс)
2. Вычесть остаток из числа
3. Поделить на 10 (еще N * N / 2 операций)
И так lg N раз, где lg = log10
Итого N2 lg N, овердофига. Если «математический» алгоритм, который вы считаете, имеет сложность M log M или быстрее, у вас печать конечного результата может занять больше времени, чем расчет.
Woodroof
19.09.2021 17:39-1Вы ошибаетесь про квадрат. Ошибка в том, что для получения остатка от деления вам не нужны все части, нужно только младшее. Для перевода достаточно переводить части и правильно обрабатывать случай "на стыке". И сложность тут линейная.

vanxant
19.09.2021 17:46+1Нет, это вы ошибаетесь. 2 ни в какой целой степени не кратно 10.
В любом случае, делить на 10 всё равно придётся.
Woodroof
19.09.2021 18:18Ну ок, для остатка. Для деления, да, нужно N^2.
Но всё равно называть это "преимуществом" странно, т.к. вырожденный случай. Например, перевод в hex-представление (тоже весьма распространённое) в варианте автора будет сложнее.

ultrinfaern
19.09.2021 17:50Откуда у вас там N^2?
В реальности (не смотрите на алгоритм в этой статье) результат деления - это сразу и остаток и частное.
Поэтому:
while (n != 0) {
// r - остаток ( это цифра для текстового представления), q - частное
div_mod(n, 10, q, r)
n = q
}

wataru
19.09.2021 17:59Пусть N — длина числа. Итераций цикла while будет O(N). Каждое деление — O(длина числа). Длина каждый раз уменьшается максимум на 1. Общее время выполнения — N+N-1+...+2+1 = O(N^2).

ultrinfaern
19.09.2021 18:24Алгоритм деления выглядит так (пусть делимое и делитель хранятся блоками):
Цикл (количество блоков делимого минус количество блоков делителя) раз
Стадия определения очередного блока часного - по двум старшим блокам делимого и одного блока делителя определить блок частного)
Стадия получения частичного остатка - цикл по всем блокам делителя - умножаем блок делителя на текущий блок часного и вычитаем из соответсующего блока текущего частичного остатка
Результат - у нас есть частное и остаток
Как можно увидеть, деление зависит только от размеров блоков. Поэтому чем больше размер блока, тем быстрее алгоритм.
Реальных операций: (разница количества блоков делимого и делителя) умножить на количество блоков делителя)

wataru
19.09.2021 19:45Как можно увидеть, деление зависит только от размеров блоков.
Что? Вы же сами написали:
Реальных операций: (разница количества блоков делимого и делителя) умножить на количество блоков делителя)
Оно зависит от длины ответа и длины делителя в блоках. Да — больше база — меньше блоков — быстрее алгоритм. Но длина блока — она же константа, потому что процессоры не могут работать со сколь угодно большими числами (именно поэтому и возникает задача вот этих вот длинных чисел). А значит эта длина блока, как константа, не влияет на O-большое.
Кстати, поскольу мы делим на 10, которое занимает 1 блок, то вот и получается, что одна операция деления будет занимать O(N), где N длина числа, как я и сказал.

wataru
19.09.2021 17:56+1- Взять остаток от деления длинного числа на 10 (это N * N / 2 операций, упс)
Неверно. Для взятия остатка на 10 надо всего O(N) операций.
И так lg N раз, где lg = log10
Берется логарифм самого числа — он пропорционален длине. Т.е. это самое N.
Но, да, если числа хранятся с двоичной базой, то операция вывода всего числа будет O(N^2), когда как для десятичных чисел это делается за O(N).
Но, если вывод в десятичной системе — редкая операция, то имеет смысл иметь базу 2^32 — ускоряются вычисления.

netch80
22.09.2021 18:38+1> Для вашего варианта с лонгами нужно для каждой цифры:
Пусть у нас в int64_t (uint64_t, неважно) число от 0 до 10^18-1. Разделив его на миллиард, получим частное и остаток оба от 0 до 10^9-1, которые влезают в int и с которыми можно дальше обращаться получением цифр по одной, как у автора. Само деление, так как оно на константу, компиляторы заменяют на обратное умножение и операция занимает, грубо говоря, 4 такта.
Точно так же можно и дальше. Если надо получить 9 цифр, можно, например, разделить дважды на 1000, и группы по 3 цифры выводить отдельными средствами — было бы зачем.
Часть таких библиотек конверсии представления (сейчас не помню названия) делят не на 10, а на 100, а потом по массиву в памяти получают сразу по 2 выходных цифры.
Вот если бы было действительно представление по основанию 2^N и между лимбами, то есть лимб с индексом 0 имел бы вес 1, 1 — 2^32, 2 — 2^64 и так далее, то тут перевод в десятичный вид был бы действительно сложнее в разы (алгоритмы есть, но они громоздкие и требуют дополнительных объяснений). Но вы ж вроде не об этом говорили?

haqreu
19.09.2021 10:39Буду краток:
apt-get install libgmp-devВо-вторых, база должна быть меньше типа int, то есть быть меньше 2^31-1.
На всякий случай, стандарт предписывает, что размер int должен быть не меньше 16 бит.

wataru
19.09.2021 12:47+3Есть несколько комментариев:
-
вместо флага natural лучше использовать какой-нибудь флаг sign, который или положителен, или отрицателен, ну или назвать is_negative на худой конец. natural как-то уж глаз режет слишком.
-
Иногда полезные операции — прибавление/умножение/деление/остаток от деления на обычный int. Вам стоит их реализовать в библиотеке. Это довольно простые функции и реализованные напрямую они кратно быстрее операции с маленьким длинным числом.
-
Про факториал вы перемудлири. Во-первых, если входное число действительно большое, то ждать выполнения кода можно вечность. Ибо вы там, как ни крути, выполняете n длинных умножений. Если n не влезает в int64 — смысла в этой операции нет вообще. Там и результат будет занимать экзобайты какие-нибудь, и считаться он будет вечность. Во-вторых вы там округляете tmp вниз, поэтому перекос происходит в правую сторону, выдавая сильно большие числа там. На самом деле можно даже не середину брать, а, скажем, делить в отношении 3:2 — тогда числа в умножении будут более сбалансированные.
-
при извлечении корня вместо сравнения n/x < x лучше делать n < x*x. Более того, можно обойтись практически без длинных умножений. Вам надо поддерживать длинные значения l, r, l^2, r^2, l*r. Через них сложениями и делениями на 2 можно получить m = (l+r)/2, m^2, m*l и m*r (m^2 надо вычислить в любом случае, чтобы сравнить его с входным числом, а из ml и mr можно считать уже только одно, когда уже поняли l или r заменяется на m). То же самое относится и к кубическому корню.
-
Вы в нескольких местах передаете LongInt по значению. Это недопустимо, если вы заботитесь о скорости. В нескольких местах вы это делаете только чтобы поменять знак операндов. Можно это обойти если реализовать приватные функции, которые вообще игнорируют знак чисел. Потом публичные функции смотрят на знаки и в зависимости от них вызывают нужную приватную функцию (например, функция сложения, если видит, что одно из слагаемых отрицательно — вызывает вычитание без проверок на знаки. Если оба отрицательны — вызвыает сложение и меняет знак у результата).
-
Пробовали умножение через быстрое преобразование Фурье? У него ассимптотика лучше, чем у карацубы. В сравнении, что и когда работает быстрее была бы ценность. Если длины чисел не слишком большие (миллионы цифр), то хватает точности double и умножение через FFT не требует даже никаких рекурсивных разбиений и работает за O((n+m) log (n+m)).

gth-other Автор
19.09.2021 13:14Спасибо за комментарий!
По поводу флага natural - тут, как бы это и абсурдно и смешно не было - надо думать. Слово signed - служебное, если назвать sign - не до конца понятно, что значит true, а что false, а is_negative немного путает, ибо положительные числа ассоциируются скорее с true, чем false.
Возможно это действительно стоит сделать! Я подумаю.
По поводу использования long long / unsigned long long вместо LongInt в аргументе функции факториала - можно, но лично я не вижу в этом особого смысла. Почти все время вычисления факториала в этой функции - сухие умножения. Остальные расчеты (по крайней мере как я понимаю, поправьте, если не прав) занимают на столько мало времени, что их можно с легкостью записать в погрешность при замерах даже на больших значениях факториала.
Тут полностью согласен. Сам что-то не додумался. Попробую, и, возможно, исправлю.
Тут тоже согласен. Так же попробую исправить.
Умножение через Фурье сделать пытался, но столкнулся с рядом сложностей. Во-первых, доступного материала в интернете по этой теме не так много как хотелось бы. Во-вторых, алгоритм все-таки сложный и требует довольно много времени на понимание.

wataru
19.09.2021 13:39+1Про фурье — вот даже на хабре есть статья: https://habr.com/ru/post/113642/
Cуть в том, что вы представляете цифры вашего длинного — это коэффициенты многочлена. Далее, перемножить 2 числа — то же самое, что перемножить такие многочлены и сделать переносы.
-

Videoman
19.09.2021 21:18+1А вы не проводили случайно замеры, как быстро будет работать ваша реализация деления в столбик, особенно для очень длинных целых, как заявлено в заголовке ?!
Дело в том, что я писал похожую реализацию для своей библиотеки slimcpplib, но не для больших целых, размер которых фактически ограничен размером доступной памяти, а для длинных, которые не помещаются в нативный размер платформы. Так вот реализация деления в виде класcического столбика, даже для 128-битных целых, для меня уже была очень медленной и неприемлемой по скорости, а это относительно небольшие числа. В итоге я остановился на алгоритме Дональда Кнута. Основная идея: мы можем разбить делимое ровно на две части и частное считать независимо оперируя только его половинами. В итоге, как только мы рекурсивно разбиваем число до приемлемого размера, мы можем использовать обычное аппаратное деление.

cadovvl
20.09.2021 11:06+1Еще не дочитал, но однозначно лайк.
Тут на днях вышла другая "обучающая" статья про длинные числа на С++, где числа хранились в строке. Боль.
Как хорошо, что на хабре еще есть и статьи вроде этой. Код глянул по-диагонали, но уже лайкнул, продолжай писать!

cadovvl
20.09.2021 12:06+2Окей, а теперь вещи, которые мне в реализации не нравятся.
* Про десятичную базу уже писали, но тут замечу, что это может быть оправдано в некоторых случаях, но тогда об этой необходимости стоило бы упомянуть.
* В каждом конструкторе - конвертер в строку - это мрак. Ну чем не устраивают просто арифметические операции? Это получается, что мы при прибавлении к длинному числу простого инта будем неявно вызывать конструктор который внутри каст к строке вызывает. У нас `d += 2` будет тормозить адски. Замерьте время цикла `for (LonfInt i(0); i < LongInt(10000000); i += 2)` . Не удивлюсь, если в этой реализации окажется медленнее чем возведение в степень.
* Число имеет смысл хранить в обратном порядке: младший разряд вv[0], старший вv.back(). И проще операции некоторые делать, и на четность проверять и т.п. Например, в вашей же реализации _zeros_leading_remove числа удаляются из начала вектора, а не конца (О(n) вместо O(1)). А теперь посмотрим на shift_right, которыйkраз вставляет 0 в начало вектора (каждая операция - O(n)). А эта операция вызывается при каждом (!!!!) сложении. Тут оптимальностью, уж простите, даже не пахнет. При записи числа в обратном порядке новые знаки добавлялись бы в конец вектора строго по необходимости, а надобность в удалении ведущих нулей просто бы отпала.
* Оператор<<который сначала преобразует в строку, а потом по символу выводит - это трусы поверх колготок. Удобнее сделать сначала оператор, а каст в строку черезstringstream. Хотя тут не все так однозначно, но текущая запись в строку... Да там одних аллокаций памяти - на каждый элемент вектора по одной.
* Давайте поговорим про аллокации памяти. Сама по себе операция долгая - системный вызов, а в многопоточном сценарии еще и требующий от ОС контроля параллельных операций (heap он как СССР - на всех один). Каждый возврат по значению числа LongInt будет требовать аллокации памяти для нового вектора, а также копирования оного. Даже если вектор небольшой, аллокация - уже дорогостоящая операция. И, внимание, вопрос: зачем у внутренних функций, типа shift_<side>, remove_zeros, mult_kara возврат по значению? Сделать их inplace не сложно, а если мне понадобится копия, я явно вызову `LongInt b = a;` и у негоshift. К чему всегда делать полное копирование числа? А оно много раз вызывается в рекурсивной реализации умножения, и я не уверен, что компилятор это сумеет оптимизировать.
Ну и еще вагонпретензиймест для улучшения.
Самая главная глобальная претензия: нельзя использовать строки как промежуточное состояние арифметических операций. Никогда. Ну и за копированием векторов надо следить: это очень частая причина деградации скорости кода.
А вообще, статья неплохая. На фоне сегодняшнего хабра - даже сильно выше среднего. К тому же, есть о чем подискутировать. Удачи в дальнейшем!
gth-other Автор
23.09.2021 18:38Спасибо за комментарий!
Согласен, что есть уйма вещей, над которыми надо поработать.
Но вот по поводу хранения числа в обратном порядке есть некоторые вопросы. Про удобство с точки зрения понятности кода не говорю, дело субъективное, но вот с точки зрения скорости реализации - хочу кое-что уточнить. Да, действительно, функции сдвига, используемые при сложении и вычитании, а также функции удаления лидирующих нулей будут так работать быстрее, но есть одно НО.
В реализации используется алгоритм Карацубы, который использует сдвиги в другую сторону. При хранении в "правильном" порядке, то есть в текущем, эти сдвиги делаются как раз за О(1), а если хранить в зеркальном - то как раз О(n). Соответственно, зеркальное хранение замедлит выполнение алгоритма умножения, а алгоритм умножения, ГОРАЗДО БОЛЕЕ зависим от сдвигов, чем вычитание и сложение. И я это еще не говорю о том, что на практике, работа с длинным умножением, длинным делением и извлечением длинных корней (а последние два активно используют умножение) гораздо более чаще встречается, чем необходимость складывать огромное количество огромных чисел. Поправьте, если не прав.

cadovvl
23.09.2021 20:04reverse в начале операции умножения, reverse в конце операции умножения - 2 операции O(n). Мне это видится куда более элегантным решением, а на фоне общей сложности умножения эти две операции будут незаметны.
Зато сложение длинного числа с маленьким (aka `x += 2`) будет выполняться почти всегда за время пропорциональное длине меньшего числа, а не делать shift по размеру большего числа.
Кстати, раз уж я снова тут, в cppreference в разделе Binary arithmetic operators делаютoperator+черезoperator+=, а не наоборот и второй аргумент передают по константной ссылке. Тоже в качестве предложений по улучшению кода: избегаем лишнего копирования.

wataru
23.09.2021 21:17+2По поводу умножения. У вас там кстати, не работающий совсем код написан. Во-первых в части, где вы делаете наивное умножение вы должны не присваивать ячейке |number_first_position + number_second_position + 1|, а добавлять туда. Потому что одно и та же сумма индесов может быть получена кучей вариантов. Например 0+3=1+2=2+1=3+0. Далее, вы там пытаетесь делать нормализацию, перекидывая в следующий разряд, но вы можете его сделать больше базы. Надо после перемножения всех цифр нормализовать число. Практически все настоящие библиотеки длинной арифметики содержат метод Normalize — который делает переносы. Потому что этот код нуджен везде.
Далее, никаких сдвигов в карацубе не надо делать и ничего копировать из входных чисел. Просто функция должна принимать в качестве параметров не Longint, а итераторы на интервал цифр в каком-то входном числе.
Зеркальное храниени ничего не замедляет нигде. И, помимо совершенно лишнего на пустом месте квадратичного алгоритма, вы при нормализации, сложении и так далее все циклы делаете вперед — это более быстро работает на современных процессорах из-за работы префетчинга.

Ingulf
23.09.2021 15:01всегда восхищали люди требующие для минимального конфига на сmake последнего (ну уже почти последнего) cmake

gth-other Автор
23.09.2021 18:40Поставил эту версию только потому что компилировал при помощи нее. Ставить более старую не стал, так как черт его знает, какие ошибки могут возникнуть на более старых версиях. Если есть необходимость - можно легко заменить циферку в файле.

Ingulf
02.10.2021 00:47Этот конфиг своего рода "hello world" только на cmake, отсюда и удивление к жесткому требованию))


ultrinfaern
Странную вы базу для чисел выбрали...
Есть прекрасная книга по арифметическим операциям - В.К.Злобин В.Л.Григорьев Программирование арифметических операций в микропроцессорах
netch80
> Странную вы базу для чисел выбрали…
У Decimal типа в .NET точно такая же — миллиард как 9 десятичных цифр в одном uint32, всего в числе 3 таких составляющих и ещё одна цифра отдельно. Так что выбор не уникальный.
ultrinfaern
Мне стало интерсно, я пошел в документацию -
The binary representation of a
Decimalvalue is 128-bits consisting of a 96-bit integer number, and a 32-bit set of flags representing things such as the sign and scaling factor used to specify what portion of it is a decimal fraction.там нет никаких двоично - десятичных представлений (да и странно это). Обычное 96 битное число.
qw1
Согласен. Первым делом смотрю базу — если не степень двойки, понимаю, что наколенная студенческая поделка и стандартной производительности библиотек длинных чисел там не увидеть никогда.