Профилирование позволяет оценить время, затрачиваемое на выполнение отдельных операций в программе. Профилирование можно выполнять как для всего кода, так и для его фрагментов.

Для начала рассмотрим профилирование фрагментов кода.

В случае работы в Jupyter notebook можно использовать так называемые “магические команды”. Для того, чтобы узнать время выполнения одной строки, нужно в её начале разместить магическую команду %time. В приведенном ниже примере в последней ячейке тетрадки создается матрица размером 10000×10000, заполненная случайными вещественными числами

Как видно, на это потребовалось 1,27 секунды. Отметим, что повторный запуск аналогичной команды потребовал уже 1,63 секунды.

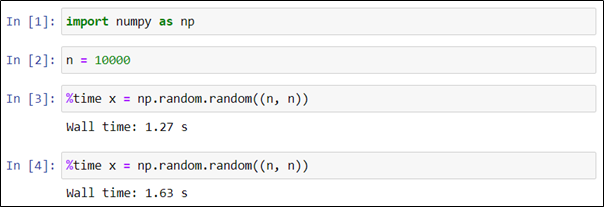
Чтобы оценить время выполнения кода в каждой из строк какой-либо ячейки, необходимо использовать магическую команду %time в каждой строке. В приведенном ниже примере создаются и перемножаются две матрицы размером 5000×5000, заполненные случайными вещественными числами.

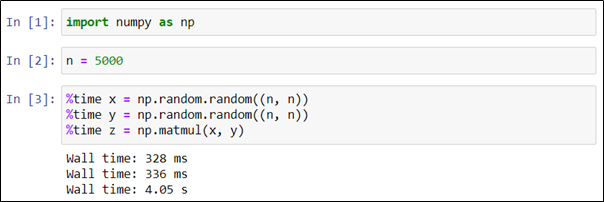
Если же нужно оценить время выполнения ячейки в целом, необходимо использовать команду %%time. Генерация двух матриц и их перемножение потребовали в сумме 4,7 секунды.

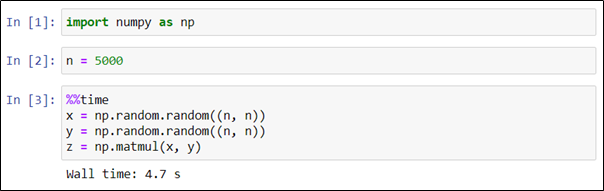
Описанные приемы позволяют получить лишь начальное представление о быстродействии кода. Как известно, единичного эксперимента недостаточно для того, чтобы составить адекватное представление о поведении исследуемой системы. Проведем серию экспериментов и возьмем среднее значение в качестве оценки времени выполнения кода. Для этого будем использовать команду %%timeit с ключом -r,  задающим количество вычислительных экспериментов.

В следующем примере мы так же генерируем и перемножаем две матрицы в серии из пяти экспериментов.

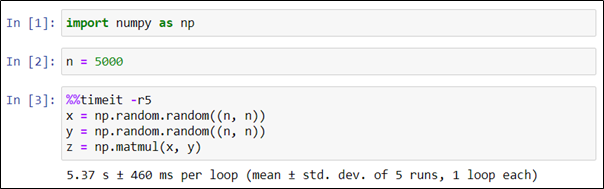
Как видно, среднее значение времени в серии экспериментов (5,37 секунды) отличается от времени единичного эксперимента, проведенного ранее (4,7 секунды).

Рассмотрим еще один пример профилирования кода.

В некоторых случаях имеет смысл сравнить несколько возможных вариантов реализации кода, чтобы выбрать из них наиболее производительный.

Известно, что значение функции “синус” для значений аргумента, близких к нулю, можно представить в виде суммы ряда Маклорена, а приближенное значение вычислить как сумму его первых двух слагаемых.

Исследуем два способа вычисления приближенного значения синуса, отличающихся способом вычисления второго слагаемого: в одном случае через трехкратное перемножение аргумента, в другом — через операцию возведения в степень. Для измерения времени снова воспользуемся командой timeit.

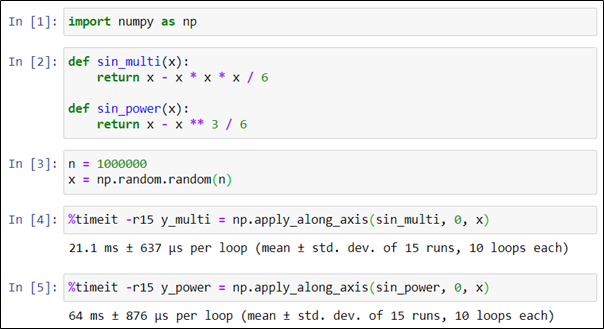
Несмотря на то, что математически эти варианты полностью эквивалентны, вариант с расчетом через перемножение аргументов приблизительно в три раза быстрее варианта с возведением в степень. Этот результат был бы совершенно не очевиден без профилирования.

Перейдем к профилированию кода программы в целом.

Представим, что есть программа min_distance_naive.py, вычисляющая наименьшее расстояние между точками на плоскости и началом координат. Координаты точек представлены матрицей размерности 1000000×2, записанной в файле points.npy. Ключевой фрагмент кода — функция  min_dist_naive.

import numpy as np

def min_dist_naive(points, base):
    r_min = float('inf')
    for p in points:
        r = ((p[0] - base[0]) ** 2 + (p[1] - base[1]) ** 2) ** (1 / 2)
        r_min = min(r, r_min)
    return r_min

points = np.load('points.npy')
origin = (0, 0)
min_dist = min_dist_naive(points, origin)
print(min_dist)

Для запуска этой программы необходимо в командной строке выполнить следующую команду:

python min_distance_naive.py

Для запуска профилирования дополним эту команду ключом -m cProfile указывающим, что для профилирования нужно использовать модуль cPython, и ключом -s time, указывающим, что результаты профилирования нужно упорядочить по времени.

python -m cPython -s time min_distance_naive.py > naive.txt

 Весь вывод, в том числе результаты профилирования, будут записаны в текстовый файл naive.txt. Анализ этого файла показывает, что время выполнения программы составило 4,369 с., суммарное время выполнения функции поиска минимального расстояния составило 4,132 с.

Теперь попробуем ускорить выполнение кода. Поскольку алгоритм решения задачи построен вокруг сравнения между собой большого количества расстояний, то, принимая во внимание монотонность функции извлечения квадратного корня, можно исключить эту функцию и сравнивать между собой квадраты расстояний. В соответствии с этой идеей несколько доработаем исходную функцию, исключив из цикла операцию извлечения квадратного корня.

import numpy as np

def min_dist_optim(points, base):
    r_min = float('inf')
    for p in points:
        r = (p[0] - base[0]) ** 2 + (p[1] - base[1]) ** 2
        r_min = min(r, r_min)
    r_min = r_min ** (1 / 2)
    return r_min

points = np.load('points.npy')
origin = (0, 0)
min_dist = min_dist_optim(points, origin)
print(min_dist)

Запустим профилирование доработанной программы.

python -m cPython -s time min_distance_optimized.py > optimized.txt

Обратимся к результатам профилирования.

В этом случае время выполнения функции составило 3,772 с.

По результатам многократного профилирования обоих вариантов и статистической обработки полученных экспериментальных данных, включающей в том числе сравнение выборок с помощью   t-критерия Уэлча, получен статистически значимый результат, свидетельствующий о том, что модифицированная функция приблизительно на 8% быстрее исходной. Таким образом, профилирование помогает выявить узкие места в коде с точки зрения производительности, сравнить разные варианты реализации алгоритмов, и в конечном счете ускорить выполнение программ. Код приведенных примеров, а также экспериментальные данные можно найти в репозитории.