Трансформеры (transformers) — это очень интересное семейство архитектур машинного обучения. Существует много хороших учебных материалов по этой теме (например — вот и вот), но в последние несколько лет трансформеры, в основном, становились всё проще. Поэтому сейчас гораздо легче, чем раньше, объяснить принципы их работы. Этот материал представляет собой попытку, что называется, «на пальцах», объяснить то, как работают современные трансформеры.

Предполагается, что читатель обладает элементарными представлениями о нейронных сетях и об алгоритме обратного распространения ошибки. Если вы хотите освежить знания в этих областях — вот видео, которое поможет вам вспомнить основы нейронных сетей, а здесь вы найдёте рассказ о том, как соответствующие принципы применяются в современных системах глубокого обучения.

Для того чтобы понять примеры кода, понадобятся практические знания фреймворка PyTorch. Но эти примеры можно и пропустить без вреда для понимания остального материала.

Здесь можно найти видеолекции о трансформерах. А в этом репозитории имеется реализация простого трансформера с использованием PyTorch.

Механизм внутреннего внимания

Фундаментальная операция, выполняемая в реализации любой архитектуры трансформера, представлена механизмом внутреннего внимания (self-attention). О происхождении этого термина мы поговорим позже. Пока постарайтесь не вкладывать в это понятие какого-то особого смысла.

Реализация механизма внутреннего внимания представлена операцией преобразования последовательности в последовательность. На входе имеется последовательность векторов, которая превращается в выходную последовательность векторов. Обозначим входной вектор как , а соответствующий выходной вектор — как . Размерность всех векторов — .

Для того чтобы получить выходной вектор yi механизм внутреннего внимания просто вычисляет среднее взвешенное значение по всем входным векторам:

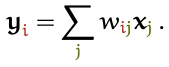
Здесь индекс проходится по всей последовательности, а сумма весов по всем значениям равняется 1. Вес — это не параметр, как в обычных нейронных сетях. Он является результатом применения особой функции к и Простейший вариант такой функции — скалярное произведение:

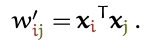
Обратите внимание на то, что — это входной вектор в той же позиции, что и текущий выходной вектор Для следующего выходного вектора мы получаем совершенно новую последовательность скалярных произведений и другую взвешенную сумму.

Скалярные произведения дают нам некое значение, находящееся между отрицательной и положительной бесконечностью, поэтому мы, чтобы привести такие значения к интервалу [0, 1], применяем функцию Softmax, а так же обеспечиваем то, что их сумма по всей последовательности равна 1:

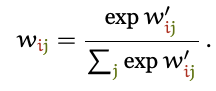
Именно так и работает механизм внутреннего внимания.

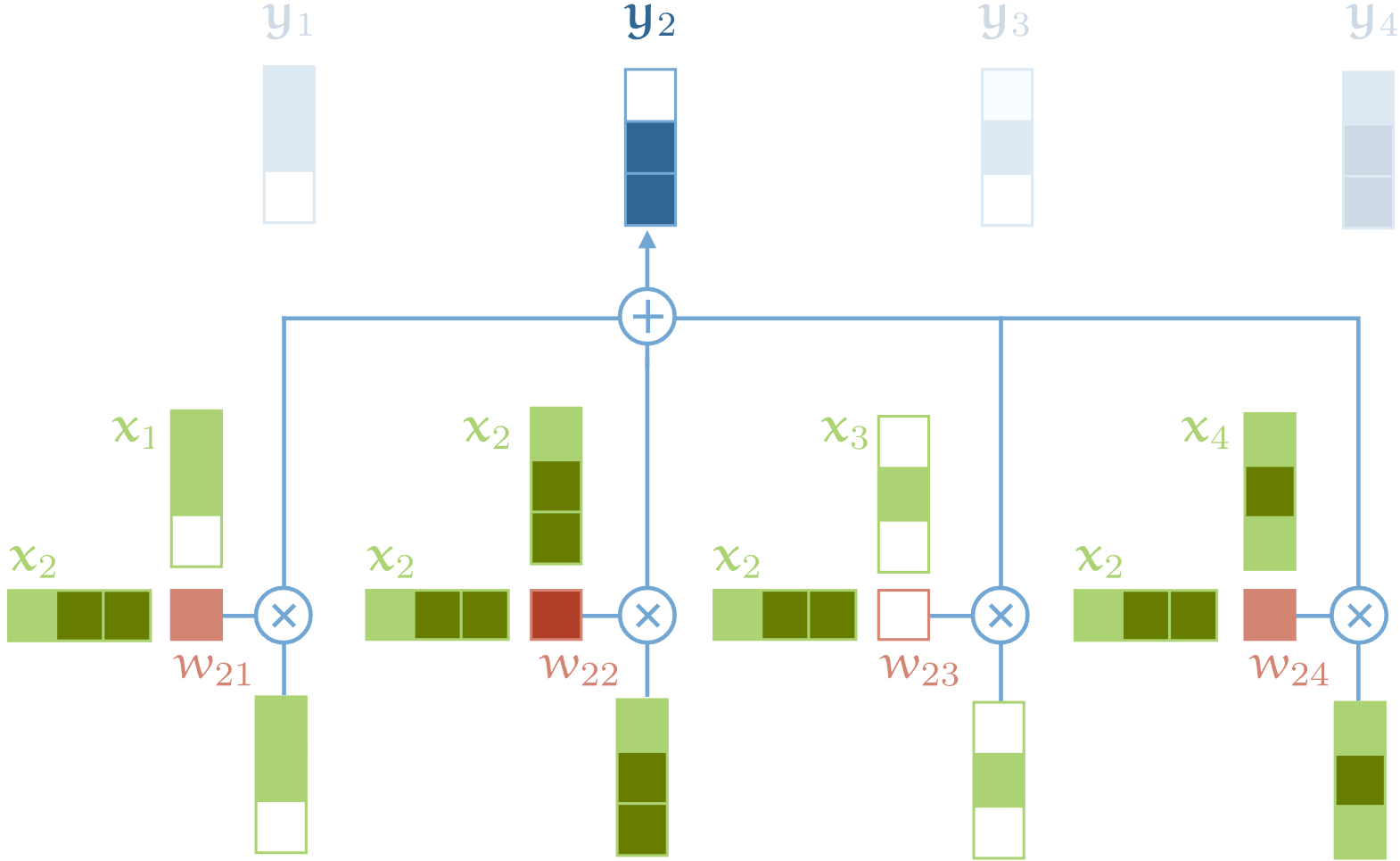
Для того чтобы создать полноценный трансформер, нам нужно ещё несколько ингредиентов, о которых мы поговорим ниже. Но то, что мы уже обсудили — это фундамент трансформеров. А ещё важнее то, что это — единственная операция во всей архитектуре, которая осуществляет перемещение информации между векторами. Все остальные операции в трансформерах выполняются над отдельными векторами входной последовательности, в ходе их выполнения взаимодействия между векторами не происходит.

Почему работает механизм внутреннего внимания?

Несмотря на крайнюю простоту механизма внутреннего внимания, совсем неочевидно то, почему он так хорошо работает. Для того чтобы немного в этом разобраться, давайте сначала посмотрим на стандартный подход к решению задачи рекомендации фильмов.

Предположим, у вас бизнес по прокату фильмов. У вас есть некие записи фильмов, имеются пользователи, и вы хотели бы рекомендовать пользователям такие фильмы, которые им, скорее всего, очень понравятся.

Один из подходов к решению этой задачи заключается в самостоятельном создании наборов характеристик (признаков) этих фильмов. Например — определяют, в какой мере тот или иной фильм является романтическим, сколько в нём экшна. Затем создаются профили пользователей, отражающие то, насколько им нравятся романтические фильмы и экшн-фильмы. Если это сделать, скалярное произведение векторов признаков даст оценку того, насколько хорошо атрибуты фильма соответствуют предпочтениям пользователя.

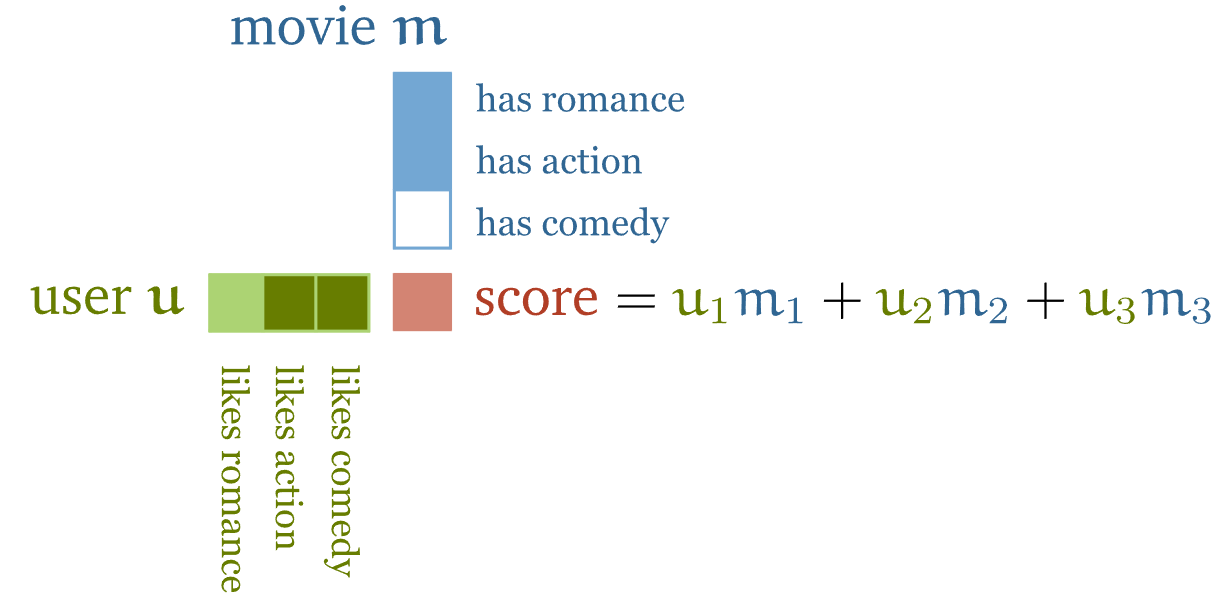
Если знаки признака, выведенного для фильма и для пользователя, совпадают, скалярное произведение даст положительный результат. Например, такое происходит, если изучаемый фильм — это фильм романтический, а конкретный пользователь любит такие фильмы. То же самое — если фильм не романтический и пользователь ненавидит романтические фильмы. Если же знаки не совпадают, то соответствующий результат будет отрицательным. Так случается, если романтический фильм сопоставить с профилем пользователя, который такие фильмы не любит, и в обратной ситуации.

Кроме того, абсолютное значение признаков указывает на то, какой вклад конкретный признак должен вносить в итоговую оценку. Фильм может быть слегка, но заметно, романтическим. А пользователь может просто предпочитать романтические фильмы, но, по большому счёту, они ему могут быть безразличны.

Конечно, сбор подобных признаков непрактичен. Аннотирование базы из миллионов фильмов — дело очень дорогое. А анализ предпочтений пользователей, выяснение того, что им нравится, а что — нет, практически невозможен.

Вместо этого признаки фильмов и предпочтения пользователей делают параметрами модели. Затем предлагают пользователям выбрать небольшое количество фильмов, которые им нравятся. После этого оптимизируют признаки пользователей и фильмов так, чтобы их скалярное произведение соответствовало бы известным предпочтениям пользователей.

Даже хотя мы не можем сообщить модели о смысле того или иного признака, на практике оказывается, что признаки, после обучения модели, реально отражают смысловое наполнение фильма.

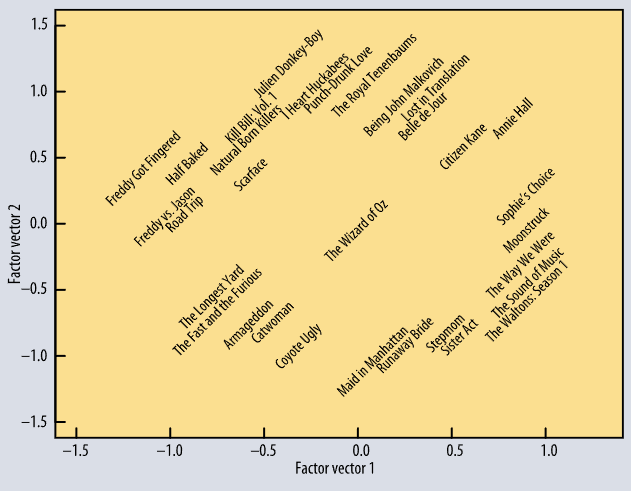
Взято отсюда.

Подробности о рекомендательных системах можно узнать, посмотрев это видео. А пока того, что уже сказано, достаточно для понимания того, как скалярное произведение векторов помогает нам в деле представления объектов и их взаимоотношений.

Именно так работает базовый принцип механизма внутреннего внимания. Предположим, перед нами — последовательность слов. Для того чтобы обработать её с помощью механизма внутреннего внимания мы назначаем каждому слову в нашем словаре числовые векторы (эмбеддинги) (значения которых будет изучать модель). Это — то, что в моделировании последовательностей известно как эмбеддинг-слой. Последовательность слов, вроде the, cat, walks, on, the, street превращается в последовательность векторов . 

Если мы передадим эту последовательность в слой механизма внутреннего внимания, выход будет представлен другой последовательностью векторов:

Здесь — это сумма по всем эмбеддингам первой последовательности, взвешенная по их (нормализованным) скалярным произведениям с

Модель пытается, путём обучения, выяснить то, какими должны быть значения vt. В результате, то, насколько «связаны» слова, полностью определяется решаемой задачей. В большинстве случаев определённый артикль the не очень сильно связан с интерпретацией других слов в предложении. В результате мы получим эмбеддинг имеющий малое или отрицательное значение скалярного произведения с характеристиками всех остальных слов. С другой стороны — для того, чтобы интерпретировать значение слова walks в этом предложении, весьма полезно будет разобраться в том, кто именно гуляет. То, что нам нужно, вероятно, выражается именем существительным, поэтому для существительных, вроде cat, и для глаголов, вроде walks, модель, скорее всего, изучит эмбеддинги и скалярное произведение которых даст высокий положительный результат.

Это — то, что поможет, на интуитивном уровне, прочувствовать механизм внутреннего внимания. Скалярное произведение выражает то, насколько связаны два вектора во входной последовательности, при этом понятие «связь» определяется задачей обучения модели. Выходные векторы — это взвешенные суммы по всей входной последовательности, а веса определены этими скалярными произведениями.

Прежде чем мы продолжим — стоит отметить следующие свойства, необычные для операций преобразования последовательностей в последовательности:

• Тут (пока) нет параметров (позже мы добавим в модель несколько параметров). Истинный смысл работы простого механизма внутреннего внимания заключается в том, что он полностью определяется той системой, которая создаёт входную последовательность. Дальнейшие механизмы, вроде эмбеддинг-слоя, обеспечивают работу механизма внутреннего внимания, изучая представления с конкретными скалярными произведениями.

• Механизм внутреннего внимания видит входные материалы в виде набора, а не последовательности данных. Если переставить элементы входной последовательности, выходная последовательность будет в точности той же самой, её элементы будут переставлены точно таким же образом (то есть — механизм внутреннего внимания эквивариантен к перестановкам). Мы несколько смягчим это, когда полностью реализуем трансформер, но механизм внутреннего внимания, сам по себе, на самом деле, игнорирует «последовательную» природу входных данных.

Реализация базового механизма внутреннего внимания в PyTorch

Ричард Фейнман сказал: «Чего не могу воссоздать, того не понимаю». Поэтому мы, двигаясь дальше, создадим простой трансформер. Начнём мы с реализации базового механизма внутреннего внимания в PyTorch.

Наша первая задача заключается в том, чтобы понять, как выразить механизм внутреннего внимания операцией умножения матриц. Примитивная реализация этого процесса, которая будет очень медленной, заключается в обходе всех векторов для вычисления весов и выходных значений.

Мы представим входные данные, последовательность векторов размерности , в виде матрицы размерности . Это, включая мини-пакетную размерность , даст нам входной тензор размера .

Набор всех необработанных скалярных произведений формирует матрицу, получить которую можно, просто умножив на результат транспонирования :

import torch
import torch.nn.functional as F

# представим, что имеется тензор x размера (b, t, k)
x = ...

raw_weights = torch.bmm(x, x.transpose(1, 2))
# - torch.bmm - это команда пакетного умножения матриц. Она
#   выполняет операции умножения над пакетами
#   матриц.

Затем, чтобы превратить необработанные веса в положительные значения, в сумме дающие единицу, мы, построчно, применяем функцию Softmax:

weights = F.softmax(raw_weights, dim=2)

И наконец, чтобы найти выходную последовательность, мы просто умножаем матрицу весов на . Это приводит к появлению пакета выходных матриц размера , строки которых представляют взвешенные суммы по строкам матрицы .

y = torch.bmm(weights, x)

Это всё. Две операции умножения матриц и одно обращение к функции Softmax позволили нам построить базовый механизм внутреннего внимания.

Дополнительные приёмы

Настоящие механизмы внутреннего внимания, используемые в современных трансформерах, задействуют три дополнительных приёма.

1. Запросы, ключи и значения

В реализации механизма внутреннего внимания каждый входной вектор xi используется тремя способами:

• Его сравнивают с каждым из других векторов для установки весов его собственного выходного вектора .

• Его сравнивают с каждым из других векторов для установки весов -ого выходного вектора .

• Он, после установки весов, участвует в вычислении взвешенной суммы, используемой для получения каждого из выходных векторов.

Эти роли часто называют запрос (query), ключ (key) и значение (value) (о том, откуда взялись эти названия, мы поговорим позже). В базовой реализации механизма внутреннего внимания, о которой мы до сих пор говорили, каждый входной вектор должен играть все три эти роли. Мы немного упрощаем жизнь модели, получая новые векторы для каждой роли. Для этого мы применяем линейную трансформацию к исходному входному вектору. Другими словами, мы добавляем три матрицы весов размером — , и и производим три линейных трансформации для каждого xi, делая это для трёх разных частей механизма внутреннего внимания:

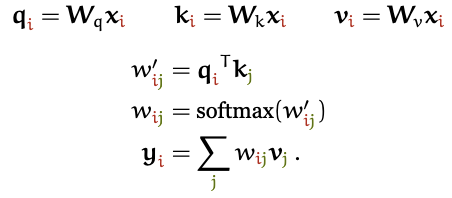
Это даёт слою механизма внутреннего внимания некоторое количество контролируемых параметров и позволяет ему модифицировать входящие вектора так, чтобы они подошли бы для тех трёх ролей, которые они должны играть.

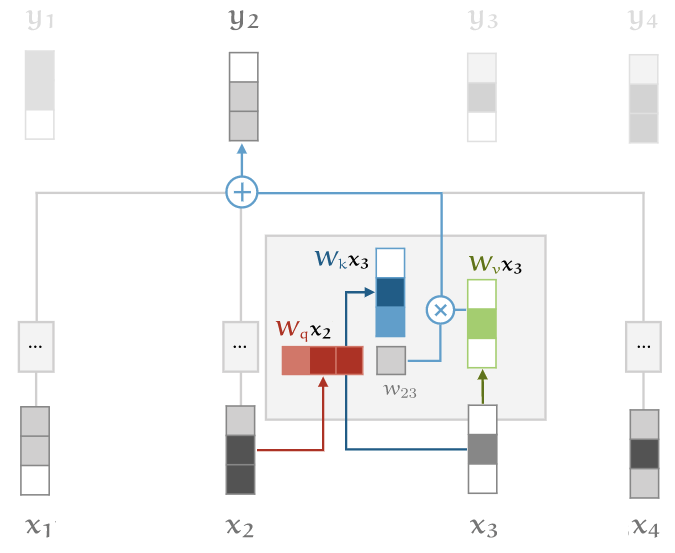
2. Масштабирование скалярного произведения векторов

Функция Softmax может испытывать сложности при обработке очень больших входных значений. Это сильно мешает алгоритму градиентного спуска, замедляет обучение модели, а может и совсем его остановить. Так как среднее значение скалярного произведения векторов растёт с ростом размерности k эмбеддинга, полезно масштабировать результаты скалярного произведения, немного уменьшая их, предотвращая тем самым чрезмерный рост входных данных функции Softmax:

Почему тут используется ? Представьте себе вектор в пространстве ℝ^k, все значения которого равняются c. Его евклидова длина — . В результате получается, что мы осуществляем деление на значение, на которое увеличение размерности увеличивает длину средних векторов.

3. Множественный механизм внутреннего внимания

И наконец — мы должны учитывать тот факт, что слово может иметь разные значения по отношению к различным соседним словам. Рассмотрим пример: mary, gave, roses, to, susan (Мэри дала розы Сьюзен). Видно, что слово gave имеет разные взаимоотношения с разными частями предложения. Слово mary обозначает того, кто что-то кому-то даёт. Слово roses — это то, что дают. А слово susan указывает на того, кто что-то принимает.

В одиночной операции механизма внутреннего внимания вся эта информация просто суммируется. Если описана будет обратная ситуация, и Сьюзен даст розы Мэри, выходной вектор будет точно таким же, как прежде, несмотря на то, что изменился смысл предложения.

Реализацию механизма внутреннего внимания можно оснастить мощной возможностью выявления различий во входных данных, скомбинировав несколько таких механизмов (индексировать их мы будем с помощью r), у каждого из которых будет собственная матрица:
. Это — блоки механизма внутреннего внимания (attention heads).

Для входа каждый блок выдаёт разный выходной вектор . Мы их конкатенируем и подвергаем линейной трансформации для того чтобы снизить их размерность, вернув её к.

Эффективная реализация множественного механизма внутреннего внимания

Проще всего понять множественный механизм внутреннего внимания можно, представив его в виде небольшого количества копий обычного механизма внутреннего внимания, применённых параллельно. Каждая из этих копий использует собственные трансформации, соответствующие ключу, значению и запросу. Работает эта схема хорошо, но для блоков операция, выполняемая механизмом внутреннего внимания, оказывается в раз медленнее, чем в обычном случае.

Но оказывается, что мы вполне можем, так сказать, усидеть на двух стульях: есть способ реализации множественного механизма внутреннего внимания, работающего примерно с той же скоростью, что и такой же механизм, представленный единственным блоком. При этом в нашем распоряжении остаются сильные стороны наличия различных матриц механизма внутреннего внимания, работающих параллельно. Для того чтобы этого достичь, мы разбиваем каждый входной вектор на фрагменты. Например, если речь идёт о входном векторе размерности 256 и о 8 блоках внутреннего внимания, мы разбиваем вектор на 8 фрагментов размерности 32. Для каждого фрагмента мы генерируем матрицы ключей, значений и запросов, тоже имеющие размерность 32. Это значит, что мы получим матрицы размером .

Мы, ради простоты, опишем ниже реализацию первого, более медленного, множественного механизма внутреннего внимания.

Для того чтобы как следует разобраться с тем, как работает более эффективная «фрагментарная» версия механизма внутреннего внимания, обратитесь к лекциям, ссылки на которые даны в начале материала.

Реализация полной версии механизма внутреннего внимания в PyTorch

Теперь создадим модуль механизма внутреннего внимания, оснащённый всяческими интересными дополнениями. Мы упакуем его в модуль PyTorch, что позволит, когда будет нужно, использовать его в каком-нибудь другом проекте.

import torch
from torch import nn
import torch.nn.functional as F

class SelfAttention(nn.Module):
  def __init__(self, k, heads=8):
    super().__init__()
    self.k, self.heads = k, heads

Мы рассматриваем блоков внутреннего внимания в виде раздельных наборов из трёх матриц , но, на самом деле, эффективнее будет скомбинировать эти матрицы для всех блоков в три матрицы , что позволит вычислять все конкатенированные запросы, ключи и значения с применением единственной операции умножения матриц.

 # Здесь вычисляются запросы, ключи и значения для всех 
    # блоков (в виде единого конкатенированного вектора)
    self.tokeys    = nn.Linear(k, k * heads, bias=False)
    self.toqueries = nn.Linear(k, k * heads, bias=False)
    self.tovalues  = nn.Linear(k, k * heads, bias=False)

    # Здесь выходы различных блоков приводятся к
    # единому k-вектору
    self.unifyheads = nn.Linear(heads * k, k)

Теперь можно реализовать вычисления, имеющие отношение к механизму внутреннего внимания (функция модуля forward). Сначала мы вычисляем запросы, ключи и значения:

  def forward(self, x):
    b, t, k = x.size()
    h = self.heads

    queries = self.toqueries(x).view(b, t, h, k)
    keys    = self.tokeys(x)   .view(b, t, h, k)
    values  = self.tovalues(x) .view(b, t, h, k)

Выход каждого линейного модуля имеет размер (b, t, h*k). Мы его перестраиваем, приводя к виду (b, t, h, k), что позволяет дать каждому блоку собственное измерение.

Далее — нужно вычислить скалярное произведение. Речь идёт об одной и той же операции, выполняемой для каждого блока, поэтому мы преобразуем данные в пакет матриц. Это позволяет нам, как и прежде, воспользоваться функцией torch.bmm(), а весь набор ключей, запросов и значений будет представлен в виде немного более крупного пакета.

Так как размерности блоков и пакетов не соответствуют друг другу, нам, прежде чем перестроить данные, нужно их транспонировать (это — ресурсоёмкая операция, но, видимо, без неё не обойтись).

# - преобразование данных блоков в пакет матриц
    keys = keys.transpose(1, 2).contiguous().view(b * h, t, k)
    queries = queries.transpose(1, 2).contiguous().view(b * h, t, k)
    values = values.transpose(1, 2).contiguous().view(b * h, t, k)

Скалярное произведение, как и прежде, можно вычислить одной операцией умножения матриц, но теперь речь идёт о запросах и ключах.

Правда мы, перед умножением матриц запросов и ключей, масштабируем их не с использованием , а с использованием . Это, при работе с длинными последовательностями, должно способствовать экономии памяти.

queries = queries / (k ** (1/4))
    keys    = keys / (k ** (1/4))

    # - получить скалярное произведение запросов и ключей, масштабировать данные
    dot = torch.bmm(queries, keys.transpose(1, 2))
    # - размер произведения, содержащего необработанные веса - (b*h, t, t)

    dot = F.softmax(dot, dim=2) 
    # - произведение теперь содержит веса, нормализованные построчно

Мы применяем механизм внутреннего внимания к значениям, что даёт нам выходные данные для каждого из блоков внутреннего внимания.

    # применить механизм внутреннего внимания к значениям
    out = torch.bmm(dot, values).view(b, h, t, k)

Для унификации блоков внутреннего внимания мы снова выполняем транспонирование, в результате размерности блоков и эмбеддинга соответствуют друг другу, и перестраиваем данные для получения конкатенированных векторов размерности kh. Затем мы пропускаем это всё через слой unifyheads для того чтобы снова свести их к размерности k.

    # вернуть h, t, унифицировать блоки внутреннего внимания
    out = out.transpose(1, 2).contiguous().view(b, t, h * k)
    return self.unifyheads(out)

Вот и всё: теперь у нас имеется реализация множественного механизма внутреннего внимания, в которой применяется масштабирование данных. Полный код можно найти здесь.

Надо отметить, что реализация этого всего может быть компактнее при использовании функции einsum, применяющей соглашение Эйнштейна о суммировании. Здесь можно посмотреть пример.

Продолжение следует…