Привет, Хабр!

Сегодня мы с вами поговорим простым языком, как защитить свои данные в облаке, даже если оно полностью захвачено злоумышленниками.

С ростом объёма данных, генерируемых, собираемых и анализируемых компьютерными системами, развивающимися семимильными шагами, скорость обработки больших данных стала решающей для многих государственных и коммерческих компаний. Развитие интернета вещей, объединяющего целую квартиру в живую и удобную экосистему, отслеживание местоположения и растущее внедрение устройств для контроля здоровья - все это открывает новые возможности для анализа и сервиса.

Однако такое распространение больших данных сопряжено и с рисками. Собранные данные часто содержат личную или корпоративную информацию, которая при попадании в не самые хорошие руки может нанести серьезный ущерб. Преступные группы создают подпольные рынки, где продают и покупают украденную информацию. Правительственные разведывательные службы нацелены на вражеские системы в целях шпионажа. В общем, опасностей достаточно. К счастью, современная криптография обладает достаточно мощными инструментами, которые помогают защитить большие данные на протяжение всего цикла их использования.

Облачные технологии на службе больших данных

Облачные инструменты стали предпочтительным выбором для обработки и анализа больших данных благодаря их сниженной стоимости, широкому доступу из сети, гибкости, регулируемому объему ресурсов и вариабельному подбору конкретного решения. О них мы сегодня и поговорим.

Итак, какие вообще угрозы существуют в облачных вычислениях? А их не так уж много, всего лишь два типа:

• Честный-но-любопытный недоброжелатель, как бы неожиданно это не звучало, честно соблюдает все протоколы обработки данных, но в то же время пытается получить не предназначенную для него информацию. Например, какая-нибудь компания (не будем тыкать пальцем), предоставляющая облачные ресурсы, может подсматривать за тем, какие данные вы загружаете и подсовывать вам соответствующую рекламу

• Злонамеренный недоброжелатель совершенно произвольно отклоняется от установленного протокола с целью в попытке нарушить конфиденциальность и целостность вычислений. Отправка искаженных сообщений, сговор с другими нарушителями порядка, возможно, даже убийство вашего котенка - эти негодяи могут использовать все, до чего доберутся и в каких угодно целях

Но что же значит "безопасность в облаке" и что мы хотим сохранить? В целом, есть три объекта нашей защиты. О некоторых я уже упомянул и тут тоже все просто:

• Конфиденциальность: все наши данные и любые их состояния (ввод, вывод, промежуточные стадии) остаются в секрете от ненадежных и враждебных субъектов

• Целостность: любое несанкционированное изменение входных данных может быть обнаружено. Более того, результаты вычислений на конфиденциальных данных являются корректными, то есть согласуются со входными данными (это для случая, если у вас происходит случайная порча данных в облаке. Такие данные теряют целостность, хотя никакого взлома не произошло)

• Доступность: владельцам данных обеспечивается доступ к их данным и вычислительным ресурсам. Противник не должен иметь возможности отключить возможность обращаться к ним

Поскольку с доступностью проблем не возникает, она обеспечивается некриптографическими методами, мы сфокусируемся на конфиденциальности и целостности.

Гомоморфное шифрование

Наконец, мы переходим с самому вкусному и интересному

Для начала дадим формальное определение

Пусть Ek(m) - шифрование сообщения m под ключом k. Схема шифрования гомоморфна относительно функции f, если существует соответствующая функция f', такая что Dk(f'(Ek(m))) = f(m), где Dk - алгоритм дешифрования под ключом k

Короче говоря, гомоморфное шифрование - это шифрование, позволяющее производить операции над зашифрованными данных без предварительной их расшифровки. Оглянитесь вокруг, и вы увидите, насколько широко используется гомоморфное шифрование: от RSA и схемы Эль-Гамаля до анонимного поиска в каком-нибудь гугле. Существуют частично гомоморфные системы, которые могут выполнять, например, только умножение(к таким относится упомянутые RSA и схема Эль-Гамаля) или только сложение.

Но только сложение или умножение - это как-то не серьезно, правда ведь? В конце концов, любой третьеклассник умеет и в то, и в то. Поэтому долгое время шел поиск алгоритма, который смог бы поддерживать эти операции одновременно. И в 2009 нас смог порадовать аспирант Стэнфордского Университета Крейг Джентри, представив первую в мире систему полностью гомоморфного шифрования. Опишем здесь простейшую его схему:

• Берем достаточно большое простое число p, которое будет секретным ключом

• Выбираем большое целое число. Если его остаток от деления на p четный, то этим числом мы шифруем 0 в бинарном представлении информации, если нечетный, то бинарную 1. Напомню, что получившаяся система является гомоморфной относительно умножения и сложения

• Далее нам полагает теорема, которая гласит, что если остатки от деления достаточно малы, то сложение и умножение шифротекстов выглядят достаточно рандомно для стороннего наблюдателя, чтобы подбор секретного ключа по полученному шифротексту был достаточно трудоемкой задачей

• С ростом количества операций над шифротекстом остаток может расти, и мы теряем нашу прекрасную теорему, а вместе с ней и безопасность шифрования

• Но тут мы использую одну хитрость: мы снова применяем шифр над шифротекстом. Получаем два уровня шифрования: старый и новый

• Расшифровываем старый шифр с помощью секретного ключа - и вот мы получаем новый шифр с гарантированно малым остатком, так как на нем еще не производились операции. Можем продолжать вычисления пока не кончатся деньги на электричество

Выглядит круто, но и у этого есть проблемы. Во-первых вычисления на шифрах занимают намного больше времени, чем на исходных сообщениях. Кроме того, необходимо, чтобы все начальные посылатели и конечные получатели данных использовали один секретный ключ, что бывает трудно реализовать. Все это необходимая плата за полную гомоморфность.

Протокол проверяемых вычислений

Гомоморфное шифрование - это, конечно, здорово, но оно обеспечивает только конфиденциальность данных. А что насчет целостности? И здесь нам нужно узнать, что такое протокол проверяемых вычислений.

Итак, у нас есть два субъекта - слабый, маломощный клиент (или верификатор) и сильный, производительный сервер (или проверяющий). Мы хотим отдать для вычислений на сервер сложную функцию f и входные данные для нее x, и получить выход функции y=f(x) и подтверждение z того, что выход y действительно является результатом работы функции f над данными x. Все, что остается клиенту - это проверить правильность сообщения z. Причем проверка результата должна быть значительно проще и эффективнее, чем непосредственное вычисление функции f. Иначе зачем вообще нам отправлять данные для вычислений на сервер?

Большинство таких систем основаны на вероятностно проверяемых доказательствах. Их замечательная особенность в том, что для доказательства подлинности вычислений нам нужно верифицировать из строки z лишь ограниченное количество символов со случайных позиций. Это позволяет снизить нагрузку на вычислительно слабого клиента.

К великому сожалению, сам по себе метод проверяемых вычислений не дает верифицируемость вычислений. Проверяющий может сохранять ответы от верификатора, на ходу подстраиваться под них и учиться менять сообщение Z так, чтобы оно проходило верификацию. Например, в самом простом случае клиент может повторять отправку функции и входных данных до тех пор, пока не верифицирует ответ. В свою очередь сервер, видя, что ему приходят одни и те же данные, будет пытаться взломать алгоритм верификации до тех пор, пока ему не поступят новые данные.

Тут можно было бы сдаться и надеяться на добрую волю и глупость злоумышленника, но не зря же я начал с гомоморфного шифрования. Свойства гомоморфного преобразования позволяют нам скрывать запросы клиента от сервера, но все еще позволяет последнему отвечать на них. Так как сервер видит данные только в зашифрованном виде, он не может узнать, как подстраивать верификационную строку. Получаем систему, сохраняющую целостность и конфиденциальность. Все просто и со вкусом.

А что там насчет производительности? А по ней все очень плохо. Даже самые производительные системы, такие как Pinocchio и SNARKS показывают себя из рук вон плохо. Pinocchio верифицирует ответ за 10 мс, однако создает подтверждение целых 144 с и использует для этого 277745 умножений. SNARKS в свою очередь проверяет ответ за 5 с, но при этом и на подтверждение уходит меньше: 31 с и 262144 операции.

Протокол конфиденциального вычисления

Описанные протоколы работают в самых мрачных случаях, когда все облако захвачено злоумышленниками и буквально из каждого его угла торчит по грозному бандитскому револьверу. Но что если мы уверены, что хотя бы часть вычислительной мощности системы остается нам верной? Могли бы мы ускорить наши алгоритмы? Разумеется, да!

Протокол конфиденциального вычисления (ПКВ) разделяет вычисление функции между частями системы так, что ни одна из сторон не может извлечь ничего полезного из данных, и только полный сбор Мстителей всех частей может восстановить изначальную информацию. Многие системы позволяют подбирать эффективность алгоритма, основываясь на максимальном предполагаемом количестве захваченных противником частей.

Проще всего работу такого протокола показать на известном примере с Элли, Брайаном и Каролиной. Допустим, все трое работают в крупных богатых компаниях важными сеньорами-программистами и получают, соответственно, 100к, 200к и 300к в месяц (и это в долларах!). Они хотят разобраться между собой, кто из них получает выше среднего (считаем среднее по ним троим), а кто не такой уж и хороший кодер, но при этом не раскрывая никому из участников своей зарплаты.

В начале каждый делит свою зарплату на три случайные части. Например, пусть у Элли это будут 50к, 30к и 20к. Одну часть она оставляет себе, а остальные отправляет друзьям, каждому по одной. То же самое делают Брайан и Кэролин. Каждый из друзей имеет по три кусочка, один свой, два чужие.

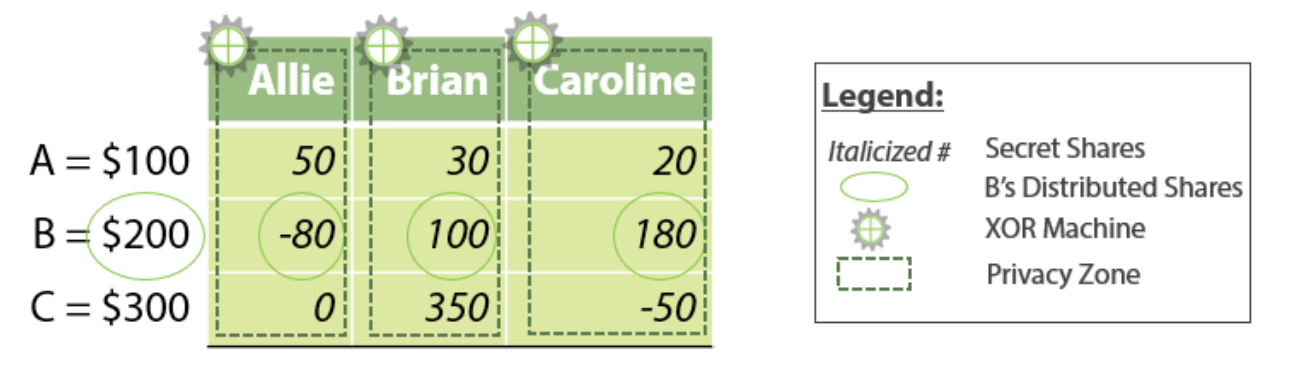
Сами по себе части зарплаты полезной информации не несут, поэтому все данные сторонних участников сохраняются в секрете. А дальше только ловкость рук и никакого мошенничества. Элли, Брайан и Кэролин складывают свои части и отправляют их другим.

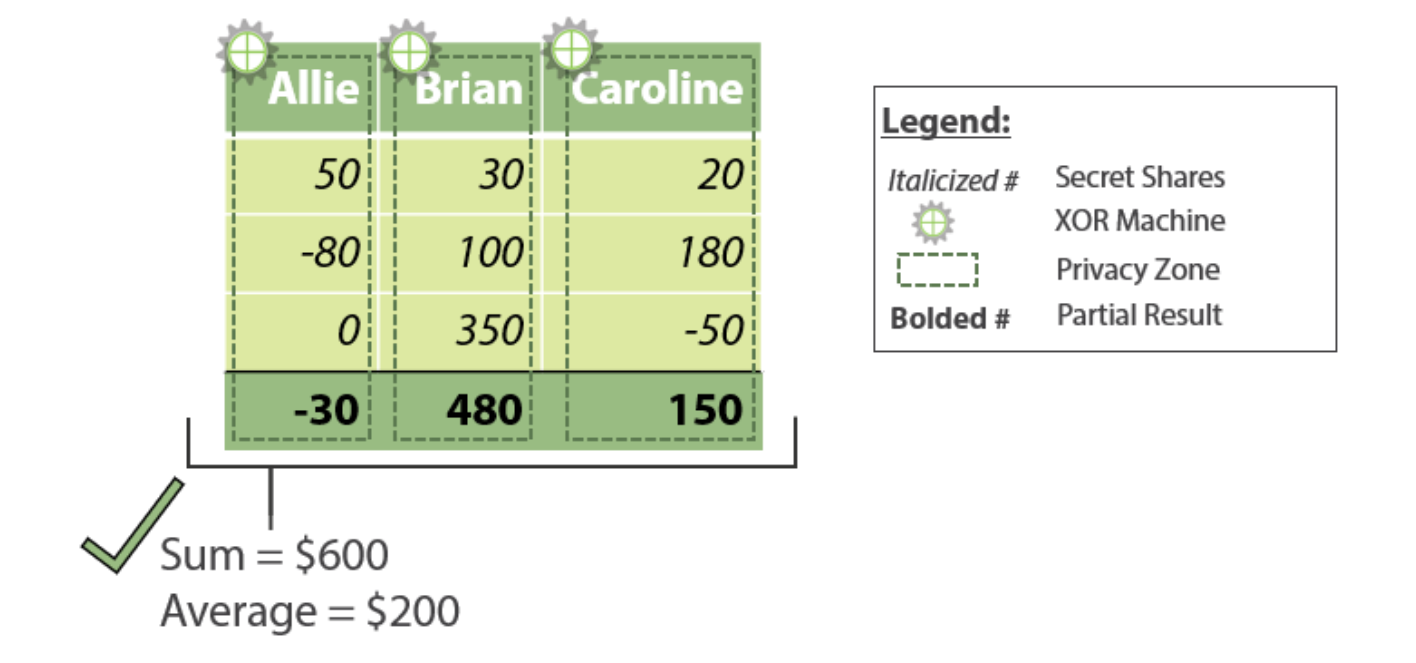
Теперь, когда каждый сложит пришедшие суммы и поделит их на количество участников, он получит ту самую среднюю зарплату. И Элли поймет, что ей пора менять работодателя.

Это работает против любопытных злоумышленников, но что насчет тех, кто не будет отправлять честно посчитанные части? Есть многочисленные расширения протокола на этот случай, самый простой (и неэффективный) из которых - это доказательство с нулевым разглашением. Благодаря этому алгоритму одна сторона (доказывающий) может подтвердить другой стороне (верификатору), что он обладает неким секретом, не раскрывая никакой информации о самом секрете. Есть милый, детский пример, во всей своей красе показывающий работу этого метода. Но сначала формальное определение.

Доказательство с нулевым разглашением должно удовлетворять трем свойствам:

• Полнота: если утверждение правдивое, то честный верификатор будет убежден в этом факте честным доказывающим

• Надежность: если утверждение ложное, никакой нечестный доказывающий, за исключением небольшой вероятности, не может убедить честного верификатора в правдивости утверждения

• Нулевая информация: никакой верификатор не может узнать ничего о выражении, кроме того, что оно правдиво

Первые два из них являются свойствами более общих интерактивных систем доказательств. Третье - это то, что определяет доказательство нулевым разглашением.

Доказательства с нулевым разглашением не являются доказательствами в математическом смысле этого слова, потому что существует некоторая вероятность того, что мошенник сможет убедить проверяющего в ложном утверждении. Другими словами, доказательства с нулевым разглашением являются вероятностными «доказательствами», а не детерминированными доказательствами. Однако есть методы, позволяющие уменьшить ошибку надежности до пренебрежимо малых значений.

А теперь небольшая история

Два наших героя, скажем, зовут их Пегги (доказывающий) и Виктор (верификатор) отправились в волшебную пещеру. В ней есть волшебная дверь, которая открывается только если произнести волшебное слово. Пару дней назад под строжайшим секретом Пегги узнала его от местных магов. Виктор же ужас как хочется понять, существует ли магия, а в частности, знает ли Пегги волшебное слово. И вот, что они придумали.

Сначала в пещеру входит Пегги и идет куда ей захочется, например, в В. Виктор стоит у входа и не видит, куда ушла Пегги. Когда она становится у двери, заходит Виктор и просит ее выйти со случайной стороны. Пегги может повезти (с шансом 50%), Виктор скажет В и девочка без какой-либо магии выходит из В. Либо Пегги не везет, и она должна назвать волшебное слово, чтобы открыть дверь и выйти из другого прохода.

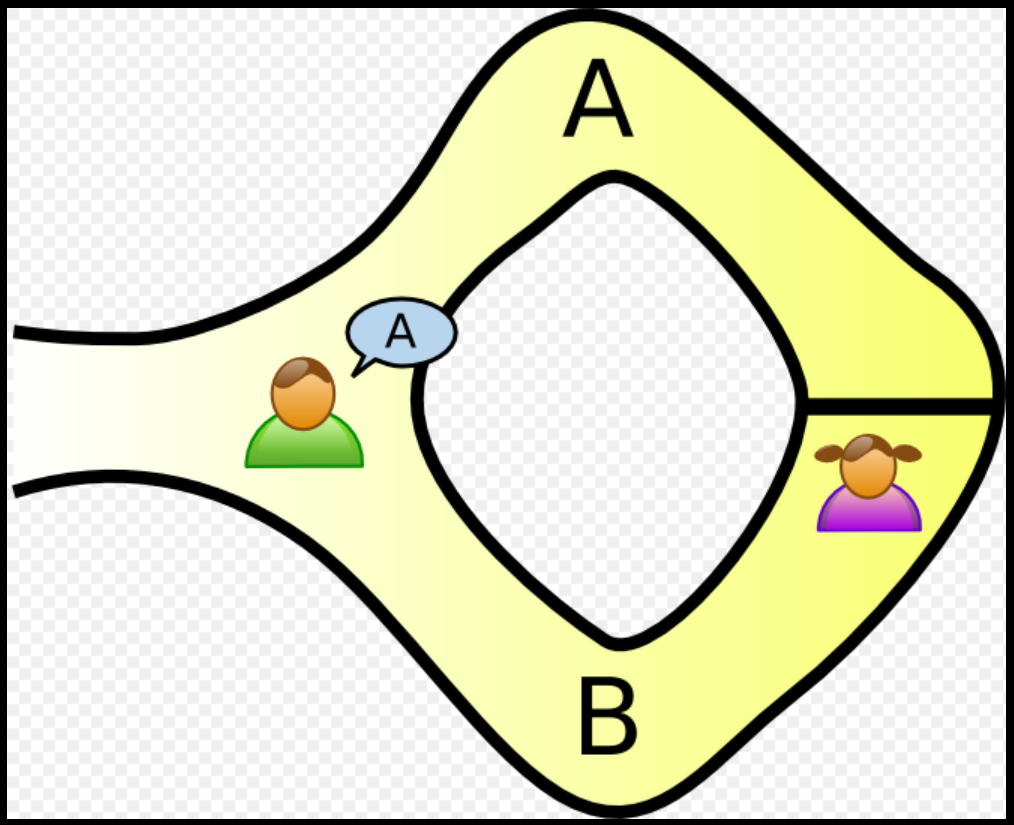
Кажется, что 50% вероятность поймать Пегги на лжи - это как-то слабовато, скажете вы. И будете правы. Но если Пегги и Виктор провернут такой трюк, скажем, 20 раз, и Пегги ни разу не выйдет из неверного прохода, то шанс того, что Пегги повезло 20 равен , или приблизительно один на миллион. Достаточно мощно, чтобы убедиться, что Пегги действительно знает волшебное слово. Если только Пегги - не самая везучая девочка в мире.

Протокол конфиденциального вычисления имеет ряд применений на практике. Из наиболее известного, датские фермеры использовали этот протокол для согласования цен на сахарную свеклу. Библиотека VIFF реализует несколько ПКВ и вычисляет один AES блок за 2.1 секунды. Несколько команд ученых (например, команда Берхарта) разрабатывают различные улучшения этого алгоритма, работая как над скоростью, так и над увеличением устойчивости против большего числа злоумышленников.

Заключение

Итак, друзья, мы прошлись по верхам современных способов защиты информации в облаке, а именно по гомоморфному шифрованию, протоколам проверяемых и конфиденциальных вычислений. Стоит отметить, что все алгоритмы имеют мощную математическую базу и строгие доказательства их работы. Также в данной статье не упоминалось про функциональное шифрование, еще один актуальный раздел криптографии, помогающий честным программистам по всему миру бороться с негодяями, которые пытаются подсмотреть, или того хуже, изменить их данные.

Очевидно, безопасность данных требуется везде, не только в сфере Big Data. Науке о шифровании уже более 4 тысяч лет, и она продолжает удивлять нас новыми открытиями и причудливыми алгоритмами. Остается только догадываться и с нетерпением ждать, что еще новенького и интересного придумают ученые из сферы криптографии. И надеяться, что квантовые компьютеры, которые поломают всю современную криптографию, станут повсеместно распространены не слишком скоро. Но это уже совсем другая история.

Спасибо за внимание!