CryptoNN: Training Neural Networks over encrypted Data. Совмещаем data privacy и нейронные сети / forpes.ru

15.12.2021 12:29

mikhail_konyk 1 1000 Источник

Привет, Хабр!

Машинное обучение и нейронные сети получили огромное распространение во многих технических областях и повсеместно используются сейчас. Известно, что большинство алгоритмов машинного обучения, а в частности и нейронные сети для своего обучения требуют больших вычислительных ресурсов. В связи с этим возникает потребность в облачных решениях и удаленных серверах. И тут же встает вопрос: как сохранить приватность данных, чтобы использовать их для обучения нейронных сетей на удаленных машинах?

В своем небольшом посте я приведу обзор метода CryptoNN из статьи CryptoNN: Training Neural Networks over Encrypted Data, который позволяет использовать для обучения нейронных сетей зашифрованные данные. Мой рассказ будет состоять из трех частей - сначала я опишу все используемые в этом подходе схемы шифрования данных, затем я разберу сам метод и основные ньюансы связанные с ним. В заключение увидим то какие результаты показывает CryptoNN на MNIST датасете.

Схемы шифрования

Все схемы шифрования используемые в данном методе основаны на функциональном шифровании(FE). В свою очередь функциональное шифрование представляет из себя метод шифрования с открытым ключом в котором пользователь позволяет вычислять от зашифрованных данных только ограниченный класс функций, путем генерации секретных ключей для этих функций. Также в отличие от методов гомоморфного шифрования, в результате использования FE мы получим сразу расшифрованный результат.

Приводятся две схемы - для вычисления скалярного произведения(FEIP) и для вычисления основных арифметических операций(FIBO). Тут я кратко опишу их составляющие.

Cхема для скалярного произведения

Вспомним определение скалярного произведения двух векторов:

$f(x,y)=\sum_{i=1}^{\eta}(x_iy_i)$

Схема FE для скалярного произведения определяется как Схема FE для скалярного произведения определяется как FEIP = (Setup, KeyDerive, Encrypt, Decrypt):

: генерируем число g и вектор , далее используя эти величины получаем публичный и секретный ключи - $mpk = (g, h_i=g^{s_i})$ , . После этого возвращаем эту пару ключей.
: возвращаем секретный ключ функции, как $sk_f = \langle y, s \rangle$
: выбираем случайное число r и вычисляем , а также $ct_i = h^r_i · g^{x_i}$ , возвращаем шифротекст .
: возвращаем дискретный логарифм по основанию g:

$g^{\langle x,y \rangle} = \prod_{i \in [\eta]}]ct_i^{y_i}/ct_0^{sk_f}$

Схема для основных арифметических операций

$f_{∆∈[+,−,∗,/]}(x, y) = x∆y,$

: генерируем числа g, затем s. $msk = s, mpk = (h, g),\ where\ h = g^s$
: возвращаем секретный ключ функции, как $sk_{f_\Delta}$ :

возвращаем commitment, . И шифротекст:
возвращаем дискретный логарифм по основанию g:

CryptoNN

Теперь перейдем к описанию самого подхода CryptoNN. Обратим внимание на схему фреймворка на рис.1

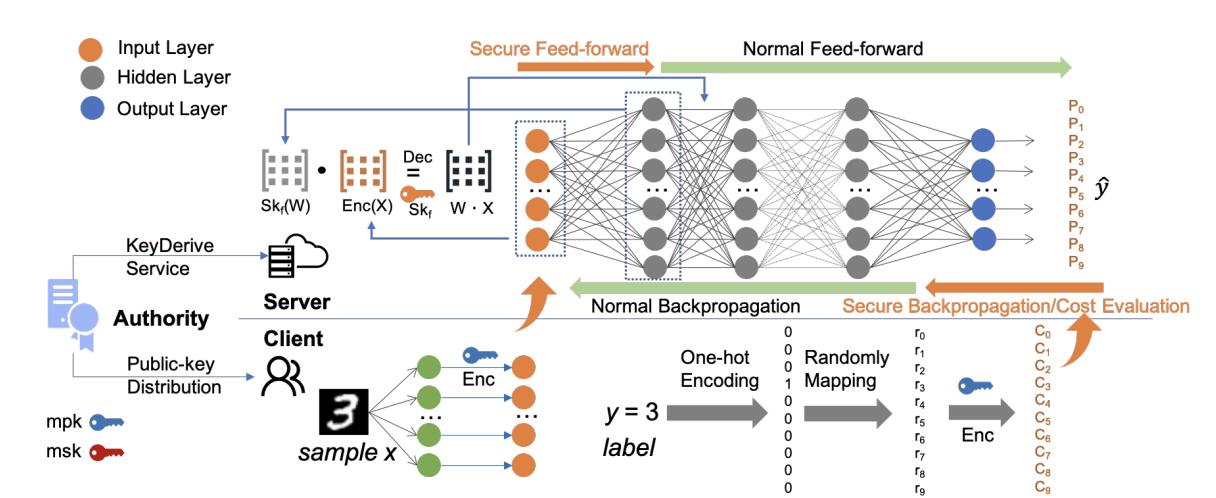
Условно можно выделить 3 части authority, server, and client.

Authority - генерирует ключи msk и mpk Также выполняет операции KeyDerive для отправки ключей sk_f серверу.

Клиент - отвечает за препроцессинг данных и используя mpk зашифровывает их. Также обрабатывает и зашифровывает таргет. После этого отправляет данные и таргет в виде зашифрованных векторов на сервер.

Сервер - собирает данные от различных пользователей. Важно лишь чтобы пользователи использовали один и тот же публичный ключ. На каждой итерации обучений получает ключи sk_f от authority для конкретной операции.

Рассмотрим значение на выходе из первой функции активации a =g(WX+b) - так было бы, если бы шифрование входных данных отсутствовало.

В схеме CryptoNN на вход сети данные подаются в зашифрованном виде, поэтому необходимо вычислять это значение следующим образом: a = g(sk_f (W) · enc(X) + b) = g(f(WX) + b)

Несмотря на то, что сервер не знает значения благодаря функциональному шифрованию он способен вычислить результат матричного произведения !

Рис.2. Псевдокод для алгоритмов работы с зашифрованными матрицами.

Выше были описаны схемы FEIP и FEBO, используя их теперь мы можем запросто реализовать все операции над матрицами(матричное умножение, поэлементное сложение и т.п.). За детальным описанием этого алгоритма рекомендую обратиться к статье(см. рис.2. - Algorithm 1: secure matrix computation scheme).

Основными отличиями такой "безопасной" нейронной сети служат шаги - secure feed-forward и secure back-propagation / evaluation. В остальном пайплайн такой же как и в обычных non-secure нейронных сетях.

Рис. 3. Алгоритм обучения нейронной сети CryptoNN.

Secure feed-forward - был описан выше, он представляет из себя вычисление результата первой функции активации, используя алгоритм Secure matrix computation scheme

Secure back-propagation / evaluation - это первый шаг backward pass'а, тут все те же правила, что и в обычном backward pass'е - используем правила взятия производной сложной функции, также помним о том, что все операции над зашифрованным таргетом Y необходимо производить с использованием алгоритма Secure matrix computation scheme.

На стадии инференса всё просто - так как выходные значения не зашифрованы в силу FE. Если же в целях безопасности необходимо, чтобы выходное значение было зашифрованным, то это запросто можно имплементировать, используя гомоморфное шифрование с последующей дешифровкой на стороне клиента.

Всё вышесказанное справедливо для полносвязных нейронных сетей. Но стоит отметить, что метод CryptoNN может быть применен, также и для сверточных нейронных сетей(CryptoCNN). Это и показывают авторы, приводя алгоритм secure convolution scheme, который использует схему шифрования FEIP.

Результаты обучения

Для экспериментов авторами был выбран популярный MNIST датасет, состоящий из grayscale изображений рукописных цифр низкого разрешения. Сама нейронная сеть CryptoCNN была построена на базе нейронной сети LeNet-5 и сравнивалась с non-crypto версией. Графики обучени, метрики качества и время обучения см ниже. По точности результаты на test сете оказались идентичными. Но видно, насколько дольше обучалась CryptoCNN сеть. Все временные издержки вызваны довольно вычислительнозатратными криптографическими операциями.

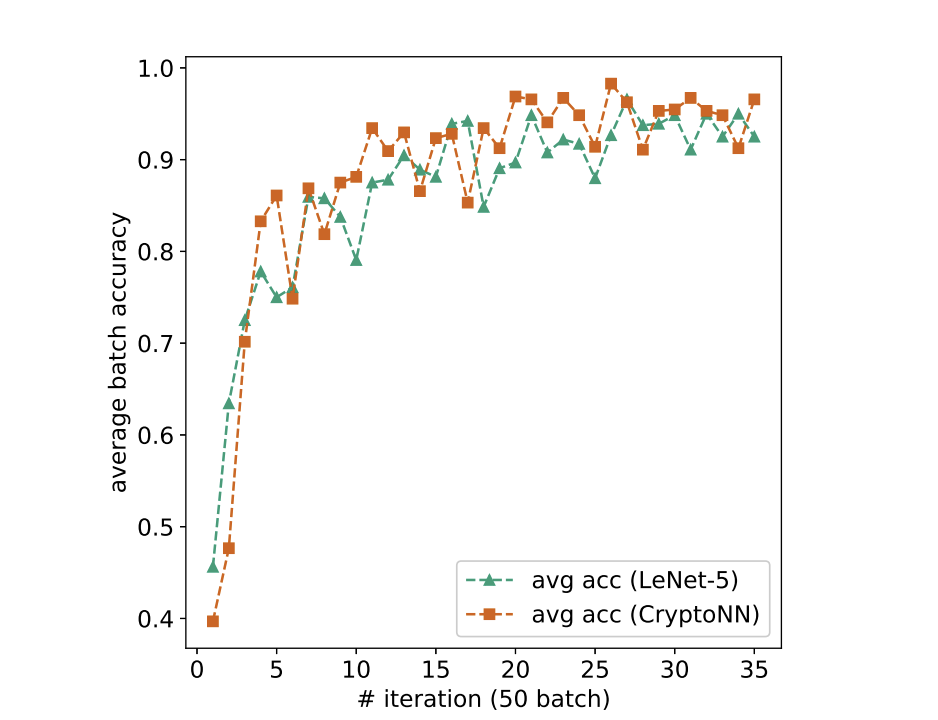
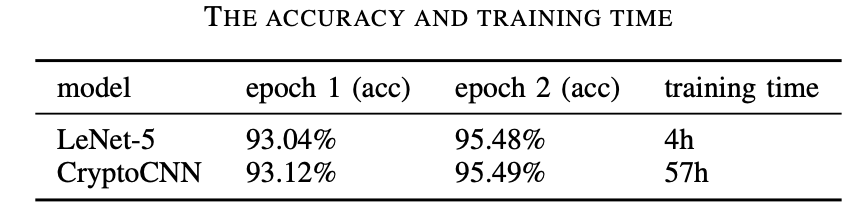
Заключение

В данной статье я привел разбор метода CryptoNN, который позволяет обучать нейронные сети на зашифрованных данных, используя схему функционального шифрования.

Данный метод может быть использован для различных вариантов нейронных сетей(в т.ч. CNN) при надлежащей реализации схем функционального шифрования. При реализации CryptoNN базе non-crypto нейронных сетей - точность модели не изменяется, при этом соблюдаются концепции data privacy и пользователи могут быть защищены от злоумышленников.

Ссылки

CryptoNN: Training Neural Networks over Encrypted Data -https://arxiv.org/pdf/1904.07303.pdf

CryptoNN: Training Neural Networks over encrypted Data. Совмещаем data privacy и нейронные сети +23