В задачах машинного обучения для обучения модели может использоваться известная целевая переменная (задачи такого типа называются «обучение с учителем»), либо модель самостоятельно учится находить закономерности с имеющихся данных, не имея заранее известные правильные результаты (такой тип задач называется «обучение без учителя»). Обучение с подкреплением (Reinforcement Learning, RL) не относится ни к первому типу, ни ко второму, однако обладает свойствами и того, и другого. Этот вид машинного обучения в настоящее время бурно развивается, разрабатывается множество теоретических алгоритмов RL [1], однако основная причина всплеска интереса заключается в множестве практических задач, в которых применяется RL, прежде всего в автоматизации, оптимизации и робототехнике. Обучение с подкреплением эффективно прежде всего там, где системе требуется анализировать окружающую среду и выбирать политику поведения с учетом получаемого отклика.
В 2013 году команда DeepMind представила алгоритм, с помощью которого они научили компьютер играть в семь игр «Atari 2600», причем сделали это без участия человека [2]. Компьютер сам совершал действия, оценивал какие из них приносят больше пользы в игре и сам формировал выигрышную стратегию. В основе этого алгоритма лежат алгоритмы RL. Сейчас игры Atari используются как бенчмарк для новых методов обучения с подкреплением. И недавний алгоритм R2D2, от все тех же DeepMind, играет лучше человека почти в 20 раз [3]. Преимущество R2D2 состоит в использовании рекуррентных нейронных сетей. Их применяли и раньше, но новый подход позволяет при этом не терять эффективность других улучшений Deep Q-learning. В этой статье рассказано какими способами удалось достичь такого результата.
Итак, обучение с подкреплением (RL) это нечто «среднее» между «обучением с учителем» (когда для любой ситуации у модели есть правильные ответы) и «обучением без учителя» (когда правильных ответов нет вообще). В RL модель которую мы обучаем, которая обычно называется «агент» (agent). Агент взаимодействует с некоторой окружающей средой (environment). Изначально для агента задается пространство действий (actions), которые можно совершать в этой среде. В ответ среда сообщает агенту некоторую награду (reward) за действие агента, а также свое новое состояние (state). Таким образом, агент накапливает знания о полученных наградах за свои действия в определённых состояниях. Целью агента является максимизация суммарно полученной награды за период. Таким образом, в RL все-таки есть «оценки» (этим RL похож на «обучение с учителем»), однако эти «оценки» не обязательно «правильные», скорее они говорят о том насколько эффективна та или иная политика действий агента.
Базовым методом RL является Q-learning [1]. В этом методе используется Q-функция, которая каждому действию ставит в соответствие возможную награду за его совершение в этом конкретном состоянии. Проще всего представить Q-функцию как таблицу, где строками являются все возможные состояния, столбцами все возможные действия, а в ячейках хранится информация о том, какую награду принесет это действие в этом состоянии.
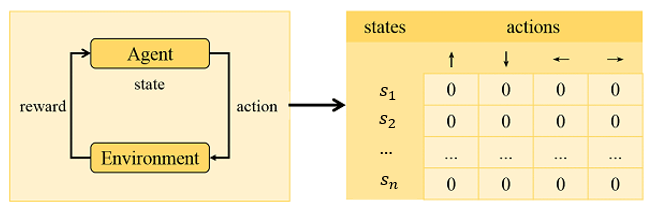
Слева схема обучения методом Reinforcement Learning. Справа пример возможной Q-таблицы
На каждом шаге мы получаем новую награду и переоцениваем прошлое значение Q-функции.
где
Давайте попробуем эту формулу объяснить на понятном языке.
Т.е. что происходит: мы пришли в текущее состояние, совершив какое-то действие![$a_t$]() и заработав награду
и заработав награду ![$r_t$]() . Теперь мы выбираем оптимальное в текущем состоянии действие для следующего шага, но заодно исправляем Q-функцию предыдущего шага, увеличив её на разницу между потенциальной наградой, доступной в текущий момент, и наградой, которую мы получили в процессе перехода в текущее состояние.
. Теперь мы выбираем оптимальное в текущем состоянии действие для следующего шага, но заодно исправляем Q-функцию предыдущего шага, увеличив её на разницу между потенциальной наградой, доступной в текущий момент, и наградой, которую мы получили в процессе перехода в текущее состояние.
Это приведет к тому, что если в текущем состоянии мы получим награду еще больше, чем на предыдущем шаге – то мы увеличим награду предыдущего шага, считая, что мы выбрали удачное действие.
И наоборот: если сейчас мы заработаем меньше, чем раньше, то и значение предыдущей награды мы уменьшим, чтобы с меньшей вероятностью пойти по этому пути – вдруг есть более выгодные.
Агент смотрит, какую максимальную награду можно получить в следующем состоянии. Это как раз добавляет ему возможность дальновидно предсказывать награду. В оценке награды учитывается не только то, что агент сможет получить сразу, но и то, какую награду он сможет получить, выбрав именно это действие и перейдя в новое состояние среды![$s_{t+1}$]() .
.
Представим, что мы учим играть бота в шахматы, и на доске следующая (синтетическая) ситуация. Предположим, что функция награда поощряет агента за каждую съеденную фигуру и, разумеется, за мат. В том случае, если агент не оценивает будущую награду, то он съест черную пешку на d7 и будет «радоваться» небольшой награде за пешку. Хотя оптимальным в том случае будет ход пешкой на c7 и дальше на c8, превращение пешки в ферзя и мат (съев вражескую пешку белые тоже побеждают, но не через 2 хода). Пример довольно искусственный, так как вознаграждать агента за съеденные фигуры нет смысла, ведь цель игры не в этом, но пример показывает, что награда здесь и сейчас не всегда лучше отложенной.
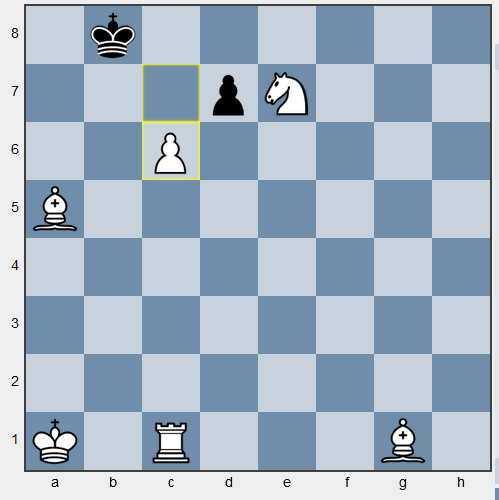
Иллюстрация примера с шахматами. c6-c7, b8-b7, c7-c8
В формуле (1) присутствуют два важных коэффициента — α и γ:
То, как агент выбирает действие, называется политикой (policy). Чаще всего используется ε-жадная политика, при которой агент всегда действует «жадно», выбирая действие, которое согласно Q-функции принесет максимальную награду. Однако, с некоторой заранее установленной вероятностью (коэффициентом спонтанности![$\epsilon$]() ) агент будет предпринимать случайные действия. Это нужно для того, чтобы можно было перепроверить состояния, которые, возможно, были оценены неверно или попробовать ещё не применявшиеся действия.
) агент будет предпринимать случайные действия. Это нужно для того, чтобы можно было перепроверить состояния, которые, возможно, были оценены неверно или попробовать ещё не применявшиеся действия.
Сейчас табличный подход мало используется на практике, так как в большинстве практических задач множество возможных действий или множество состояний являются очень большими, и табличный метод не обучает модель или обучает, но слишком долго. В случае если множество состояний является непрерывным, а не дискретным (например, положение руки робота в пространстве), то записать все состояния в таблицу вовсе не получится. Для этого используют аппроксимацию Q-функции, в том числе с помощью нейросети, такой подход называют Deep Q-learning [2].
Подробно теория и практика Q-learning изложена в классической книге Саттона и Барто «Обучение с подкреплением» [1], являющейся обязательной к прочтению для изучающих RL. Множество исследований отдельных алгоритмов и подходов в RL опубликованы в arxiv, researchgate и других источниках. Ссылки на рассмотренные в данной статье работы приведены в конце.
Далее речь пойдет про память агента, то есть возможность определять действия, основываясь не только на текущем наблюдении, но и на прошлых состояниях среды. Q-функция позволяет оценить будущую награду агента за действие в текущем состоянии. Однако в зависимости от того, как агент пришел в это состояние, награда за одно и то же действие может различаться. Полезно научиться смотреть не только вперед, но и назад.
Представим, что мы обучаем бота для игры, где возможны два варианта развития событий. В первом случае агент участвует в сражении и получает награду за каждую победу над врагом, и штраф в случае поражения. В другом случае агент добирается до укрытия и прячется там. В укрытии агента невозможно уничтожить, но и сам он не может уничтожить оппонента. В начале игры агент не умеет сражаться и часто проигрывает противникам, получая отрицательную награду. Это означает, что агент предпочел бы не сражаться вовсе. Попав в убежище, он получает нулевую награду и не будет оттуда выходить. Все другие действия Q-функция будет оценивать как отрицательные. Как итог мы обучили агента не играть в игру, а сидеть в укрытии (тактика каждого первого игрока в «Battle Royal»).
И хотя существует коэффициент спонтанности![$\epsilon$]() , это мало поможет. Агент выйдет из убежища и затем, скорее всего, будет уничтожен (он все ещё не обучился сражению), и Q-функция ещё ниже оценит ценность выхода из убежища, то есть агент ещё раз убедится, что сидеть в убежище выгодно. Чтобы преодолеть эту ситуацию с помощью одной лишь ε -жадной стратегии, нужно много раз выйти из убежища и одолеть противника, для чего потребуется очень много повторений игры. Можно придумать способы решения этой проблемы, например, штрафовать агента за долгий простой без награды. Но в общем случае Q-обучение никак не застраховано от проблемы локального максимума, когда стратегия приносит некоторую награду, но не максимально возможную, а часть среды, действия в которой могут быть очень ценными, просто не исследована.
, это мало поможет. Агент выйдет из убежища и затем, скорее всего, будет уничтожен (он все ещё не обучился сражению), и Q-функция ещё ниже оценит ценность выхода из убежища, то есть агент ещё раз убедится, что сидеть в убежище выгодно. Чтобы преодолеть эту ситуацию с помощью одной лишь ε -жадной стратегии, нужно много раз выйти из убежища и одолеть противника, для чего потребуется очень много повторений игры. Можно придумать способы решения этой проблемы, например, штрафовать агента за долгий простой без награды. Но в общем случае Q-обучение никак не застраховано от проблемы локального максимума, когда стратегия приносит некоторую награду, но не максимально возможную, а часть среды, действия в которой могут быть очень ценными, просто не исследована.
Для того, чтобы исправить эту проблему, был разработан алгоритм, учитывающий «опыт агента», Experience Replay [4]. Пусть теперь агент сохраняет все свои действия и награды за них в буфер. Получается массив данных, в котором сохранены наборы или траектории:![$(s_t, a_t, r_t, s_{t+1})$]() — в такой последовательности сохраняется информация о том, какое действие принесло какую награду при переходе из состояния
— в такой последовательности сохраняется информация о том, какое действие принесло какую награду при переходе из состояния ![$s_t$]() в состояние
в состояние ![$s_{t+1}$]() (т. е. все необходимое, чтобы сделать шаг обучения Q-функции). Затем при обучении траектории случайным образом выбираются из буфера.
(т. е. все необходимое, чтобы сделать шаг обучения Q-функции). Затем при обучении траектории случайным образом выбираются из буфера.
Теперь агент учится не только на состоянии среды в данный момент, но и на прошлых состояниях. До этого агент учился лишь на той части среды, где он сейчас находится (в нашем случае – заходил в убежище и видел только его), теперь же агент обучается на опыте, полученном, в том числе, пока шел до этого убежища, а по дороге мог получить положительную награду (которая бы затерялась на фоне постоянных поражений и отрицательных наград). C буфером траекторий такой опыт будет воспроизводиться в памяти и больше влиять на изменение Q-функции.
Помимо этого, Experience Replay помогает более эффективно использовать накопленный опыт за счет его многократного изучения. Это полезно в случаях, когда получение нового опыта в среде может быть дорогим.
В классическом Experience Replay выбор каждой траектории из буфера памяти равновероятен. Однако, не все действия одинаково полезны для агента. К записям в буфере можно добавить веса, которые будут показывать насколько ценным для обучения нейросети был этот опыт [5]. Чем больше вес траектории, тем больше вероятность её выбора для обучения. Это позволяет чаще проигрывать полезный опыт и меньше выбирать бесполезный. Но как оценить накопленный опыт? Здесь нам и пригодится понятие TD-ошибки.
Абсолютная TD-ошибка, по сути, показывает насколько изменяется оценка Q-функции. Чем больше модуль TD-ошибки, тем большую корректировку мы провели, и тем больше мы обучились. Другими словами, мы хотим повторять тот опыт, который привел к заметной разнице между ожидаемой и реальной наградой, то есть заставил нейросеть многому научиться.
Если применить такой подход к примеру с бункером выше, то больший вес будет иметь опыт, когда агент сражался и побеждал – в этот момент мы дали новую оценку действию «сражаться» и получили высокую TD-ошибку. Этот опыт будет повторен многократно, и со временем у действия «сражаться» уже будет положительная ожидаемая награда. Если же агент спрячется в бункер, он не будет получать никакой новой информации. Была у действия награда 0 – осталась 0. Такому действию будет поставлен низкий приоритет во время воспроизведения опыта, потому что оно и так уже хорошо оценено.
Если внимательно посмотреть, то такой подход приближает нас к обучению с учителем. Теперь есть некоторый датасет (пусть и формирующийся динамически), на котором обучается нейросеть. Значит, появляется возможность использовать и преимущества обучения с учителем.
Агент собирает действия в буфер и независимо от этого обучается. Соответственно, задачу наполнения буфера и задачу обучения нейросети можно отделить друг от друга. Для этого была предложена архитектура Ape-x [6]. Нейросеть, используемую как функцию оценки ценности действия, назвали Learner, а агента, выполняющего действие в среде, назвали Actor. Очевидно, Actor может быть не один. Каждый Actor имеет свой собственный экземпляр окружающей среды, что позволяет накапливать опыт гораздо быстрее. Однако, все полученные траектории вида![$(s_t, a_t, r_t, s_{t+1})$]() записываются в один общий буфер Replay, по опыту из которого учится нейросеть. Learner также расставляет в буфере приоритеты, как описано выше.
записываются в один общий буфер Replay, по опыту из которого учится нейросеть. Learner также расставляет в буфере приоритеты, как описано выше.
Каждый Actor имеет нейросеть с одними и теми же весами, полученными из Learner. Learner учится постоянно, однако обновление нейросети в Actor происходит периодически, чтобы возможные скачки в поведении среды (возможно, вызванные шумом) не так сильно влияли на обучение.
Ниже представлена иллюстрация этой архитектуры:
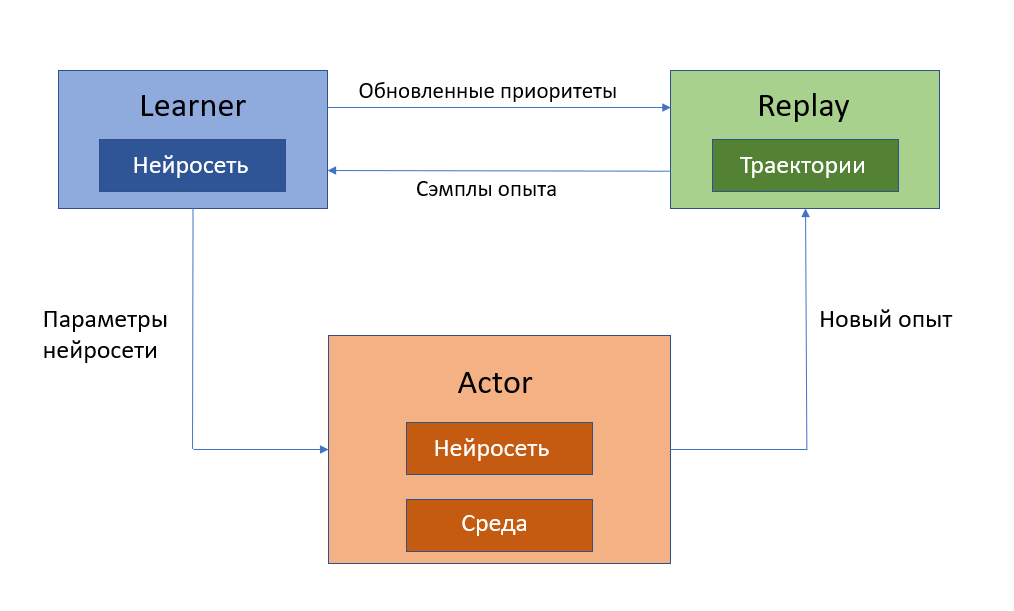
Experience replay хоть и хранит прошлые действия, но используется только для обучения нейросети. Решение о действии в состоянии все ещё принимается только на основе наблюдаемого состояния, без учета предыдущих. Хотелось бы добавить нейросети память для более точного описания среды в текущий момент, например, использовать рекуррентные нейронные сети (Recurrent Neural Network, RNN). Причем сделать это так, чтобы не потерять преимущества архитектуры Ape-X.
Здесь возникает проблема — нужно, чтобы наша RNN училась. Сейчас сохраненный опыт из буфера вытаскивается псевдослучайным образом (чаще выбираются действия с большим приоритетом), но из-за этого рушится порядок того, как среда отвечала на разные действия, а значит RNN не выявит никаких закономерностей и не обучится (это как если бы в задаче машинного перевода на вход нейросети подавалось не предложение в правильном порядке, а случайно перемешанные слова из этого предложения). Для решения этой проблемы была создана архитектура агента под названием Recurrent Replay Distributed DQN или R2D2 [2].
Для использования RNN будем хранить не отдельные шаги, а целые последовательности фиксированной длины, состоящие из идущих друг за другом траекторий![$(s, a, r)$]() (здесь мы уже не храним следующее состояние
(здесь мы уже не храним следующее состояние ![$S_{t+1}$]() , так как траектории записываются последовательно, а значит информация о следующем состоянии хранится в следующей траектории). В оригинальной статье используют последовательности длиной 80, которые перекрывают друг друга на 40 шагов (40 последних шагов последовательности 1 это 40 первых шагов последовательности 2). Помимо этого, последовательности никогда не выходят за границы эпизода игры.
, так как траектории записываются последовательно, а значит информация о следующем состоянии хранится в следующей траектории). В оригинальной статье используют последовательности длиной 80, которые перекрывают друг друга на 40 шагов (40 последних шагов последовательности 1 это 40 первых шагов последовательности 2). Помимо этого, последовательности никогда не выходят за границы эпизода игры.
Встает вопрос, как во время обучения, при перескакивании с одной последовательности на другую (используется тот же подход Prioritized Experience Replay, но уже к траекториям) инициализировать скрытое состояние RNN?
Самая простая идея – инициализировать его нулями. Это не очень хорошо, так как нули не несут никакой информации. Можно попробовать хранить рядом с каждой траекторией скрытое состояние, которое образовалось при прошлом обучении на этой траектории. Это тоже не очень хороший подход, так как нейросеть обучается и сохраненное состояние может сильно отставать от создаваемого более поздней версией нейросети.
Для решения этой проблемы авторы статьи предлагают использовать Burn-in период. Давайте инициализируем состояние сначала нулями или прошлым состоянием, как описано выше, прогоним несколько траекторий из сохраненного опыта, не обучаясь, а затем начнем обучать нейросеть как обычно. За эти несколько пропущенных шагов скрытое состояние должно достаточно обновиться, и при этом RNN не учится на плохо инициализированных состояниях.
Рекуррентные сети позволили значительно улучшить эффективность агента.
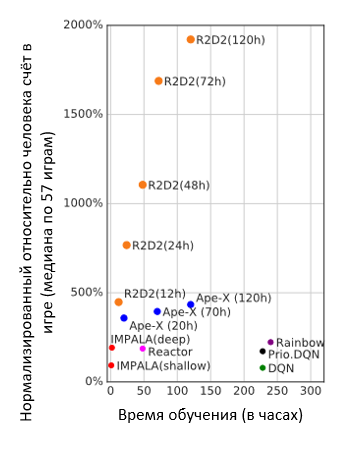
Медианное значение очков относительно человека, набираемых агентом (средние очки человека – 100%) и время, затраченное на обучение в зависимости от архитектуры.
Проследим проделанный путь. Для того, чтобы агенту принимать решение как действовать в данной ситуации, нужно дать оценку всем возможным действиям. Делать это с помощью таблицы возможно, но накладывает заметные ограничения. Из-за этого таблицу заменили нейросетью. Затем нейросети добавили буфер памяти, который позволяет избегать ситуаций, в которых агент взаимодействует лишь с частью окружающей среды – той, которую он непосредственно наблюдает сейчас. Некоторые записи в памяти ценнее для обучения, чем другие, поэтому было предложено расставлять им приоритеты. Задачи обучения и сбора информации о среде теперь разделимы, и можно отдельно собирать информацию в буфер, и отдельно обучать политику. После чего, не разрушая предыдущих наработок, в политику добавлен слой LSTM, который обучается благодаря тому, что в буфере хранятся сразу целые траектории и используется burn-in период.
В этой статье рассмотрены только вопросы, касающиеся буфера памяти и его разных модификаций. Например, в R2D2 ещё используется технология Double Q-learning, а Ape-X базируется на агенте Rainbow [7]. Rainbow, в свою очередь, является объединением нескольких способов улучшения Deep Q-learning. Для деталей лучше прочить оригинальную статью по Rainbow [7], а оттуда перейти к более детальному рассмотрению заинтересовавших «трюков» с deep Q-learning.
Реализация R2D2 существует во фреймворке Acme [8]. В качестве среды используем игру Time Pilot для приставки Atari 2600. Согласно графику из статьи [2], метод R2D2 в этой игре показывает себя лучше, чем Ape-X.

По оси ординат – среднее суммарное вознаграждение агента. По оси абсцисс – кол-во эпох. Оранжевая линия – R2D2, синяя – Ape-X, зеленая – R2D2 без RNN.
Обучим бота для этой игры. Цель – управляя синим самолетиком в центре экрана сбить вражеские желтые самолетики, и при этом не врезаться в них. Вот результат обучения на CPU в течении примерно двух суток:

Для обучения использована среда из библиотеки Gym [8]. Код для использования фреймворка Acme и среды Atatri 2600 можно посмотреть здесь [10]:
В 2013 году команда DeepMind представила алгоритм, с помощью которого они научили компьютер играть в семь игр «Atari 2600», причем сделали это без участия человека [2]. Компьютер сам совершал действия, оценивал какие из них приносят больше пользы в игре и сам формировал выигрышную стратегию. В основе этого алгоритма лежат алгоритмы RL. Сейчас игры Atari используются как бенчмарк для новых методов обучения с подкреплением. И недавний алгоритм R2D2, от все тех же DeepMind, играет лучше человека почти в 20 раз [3]. Преимущество R2D2 состоит в использовании рекуррентных нейронных сетей. Их применяли и раньше, но новый подход позволяет при этом не терять эффективность других улучшений Deep Q-learning. В этой статье рассказано какими способами удалось достичь такого результата.
Коротко об RL и Q-learning
Итак, обучение с подкреплением (RL) это нечто «среднее» между «обучением с учителем» (когда для любой ситуации у модели есть правильные ответы) и «обучением без учителя» (когда правильных ответов нет вообще). В RL модель которую мы обучаем, которая обычно называется «агент» (agent). Агент взаимодействует с некоторой окружающей средой (environment). Изначально для агента задается пространство действий (actions), которые можно совершать в этой среде. В ответ среда сообщает агенту некоторую награду (reward) за действие агента, а также свое новое состояние (state). Таким образом, агент накапливает знания о полученных наградах за свои действия в определённых состояниях. Целью агента является максимизация суммарно полученной награды за период. Таким образом, в RL все-таки есть «оценки» (этим RL похож на «обучение с учителем»), однако эти «оценки» не обязательно «правильные», скорее они говорят о том насколько эффективна та или иная политика действий агента.
Базовым методом RL является Q-learning [1]. В этом методе используется Q-функция, которая каждому действию ставит в соответствие возможную награду за его совершение в этом конкретном состоянии. Проще всего представить Q-функцию как таблицу, где строками являются все возможные состояния, столбцами все возможные действия, а в ячейках хранится информация о том, какую награду принесет это действие в этом состоянии.

Слева схема обучения методом Reinforcement Learning. Справа пример возможной Q-таблицы
На каждом шаге мы получаем новую награду и переоцениваем прошлое значение Q-функции.
где
-
— Q-функция на текущем шаге;
-
— действие (action) на шаге t;
-
— награда (reward), полученная за действие
;
-
— состояние (state) в которое перешла среда после действия
;
-
— отложенное вознаграждение.
Давайте попробуем эту формулу объяснить на понятном языке.
Т.е. что происходит: мы пришли в текущее состояние, совершив какое-то действие
Это приведет к тому, что если в текущем состоянии мы получим награду еще больше, чем на предыдущем шаге – то мы увеличим награду предыдущего шага, считая, что мы выбрали удачное действие.
И наоборот: если сейчас мы заработаем меньше, чем раньше, то и значение предыдущей награды мы уменьшим, чтобы с меньшей вероятностью пойти по этому пути – вдруг есть более выгодные.
Агент смотрит, какую максимальную награду можно получить в следующем состоянии. Это как раз добавляет ему возможность дальновидно предсказывать награду. В оценке награды учитывается не только то, что агент сможет получить сразу, но и то, какую награду он сможет получить, выбрав именно это действие и перейдя в новое состояние среды
Представим, что мы учим играть бота в шахматы, и на доске следующая (синтетическая) ситуация. Предположим, что функция награда поощряет агента за каждую съеденную фигуру и, разумеется, за мат. В том случае, если агент не оценивает будущую награду, то он съест черную пешку на d7 и будет «радоваться» небольшой награде за пешку. Хотя оптимальным в том случае будет ход пешкой на c7 и дальше на c8, превращение пешки в ферзя и мат (съев вражескую пешку белые тоже побеждают, но не через 2 хода). Пример довольно искусственный, так как вознаграждать агента за съеденные фигуры нет смысла, ведь цель игры не в этом, но пример показывает, что награда здесь и сейчас не всегда лучше отложенной.

Иллюстрация примера с шахматами. c6-c7, b8-b7, c7-c8
В формуле (1) присутствуют два важных коэффициента — α и γ:
- Коэффициент
определяет то, насколько отложенная награда будет весомой. Так как среда может быть нестабильна или агент может не до конца её изучить, то последующее вознаграждение может быть вычислено неправильно. Поэтому при оценке Q-функции разумно отдавать меньшее предпочтение отложенным результатам.
- Часть
в формуле (1) называется Temporal difference error, или TD-ошибка. Эта величина описывает то, насколько мы изменили оценку рассматриваемой Q-функции после очередного действия. Коэффициент
регулирует влияние только что полученной TD-ошибки на старое значение Q-функции. Понятие TD-ошибки пригодится нам позже.
То, как агент выбирает действие, называется политикой (policy). Чаще всего используется ε-жадная политика, при которой агент всегда действует «жадно», выбирая действие, которое согласно Q-функции принесет максимальную награду. Однако, с некоторой заранее установленной вероятностью (коэффициентом спонтанности
Сейчас табличный подход мало используется на практике, так как в большинстве практических задач множество возможных действий или множество состояний являются очень большими, и табличный метод не обучает модель или обучает, но слишком долго. В случае если множество состояний является непрерывным, а не дискретным (например, положение руки робота в пространстве), то записать все состояния в таблицу вовсе не получится. Для этого используют аппроксимацию Q-функции, в том числе с помощью нейросети, такой подход называют Deep Q-learning [2].
Подробно теория и практика Q-learning изложена в классической книге Саттона и Барто «Обучение с подкреплением» [1], являющейся обязательной к прочтению для изучающих RL. Множество исследований отдельных алгоритмов и подходов в RL опубликованы в arxiv, researchgate и других источниках. Ссылки на рассмотренные в данной статье работы приведены в конце.
Далее речь пойдет про память агента, то есть возможность определять действия, основываясь не только на текущем наблюдении, но и на прошлых состояниях среды. Q-функция позволяет оценить будущую награду агента за действие в текущем состоянии. Однако в зависимости от того, как агент пришел в это состояние, награда за одно и то же действие может различаться. Полезно научиться смотреть не только вперед, но и назад.
Experience Replay
Представим, что мы обучаем бота для игры, где возможны два варианта развития событий. В первом случае агент участвует в сражении и получает награду за каждую победу над врагом, и штраф в случае поражения. В другом случае агент добирается до укрытия и прячется там. В укрытии агента невозможно уничтожить, но и сам он не может уничтожить оппонента. В начале игры агент не умеет сражаться и часто проигрывает противникам, получая отрицательную награду. Это означает, что агент предпочел бы не сражаться вовсе. Попав в убежище, он получает нулевую награду и не будет оттуда выходить. Все другие действия Q-функция будет оценивать как отрицательные. Как итог мы обучили агента не играть в игру, а сидеть в укрытии (тактика каждого первого игрока в «Battle Royal»).
И хотя существует коэффициент спонтанности
Для того, чтобы исправить эту проблему, был разработан алгоритм, учитывающий «опыт агента», Experience Replay [4]. Пусть теперь агент сохраняет все свои действия и награды за них в буфер. Получается массив данных, в котором сохранены наборы или траектории:
Теперь агент учится не только на состоянии среды в данный момент, но и на прошлых состояниях. До этого агент учился лишь на той части среды, где он сейчас находится (в нашем случае – заходил в убежище и видел только его), теперь же агент обучается на опыте, полученном, в том числе, пока шел до этого убежища, а по дороге мог получить положительную награду (которая бы затерялась на фоне постоянных поражений и отрицательных наград). C буфером траекторий такой опыт будет воспроизводиться в памяти и больше влиять на изменение Q-функции.
Помимо этого, Experience Replay помогает более эффективно использовать накопленный опыт за счет его многократного изучения. Это полезно в случаях, когда получение нового опыта в среде может быть дорогим.
Prioritized Experience Replay
В классическом Experience Replay выбор каждой траектории из буфера памяти равновероятен. Однако, не все действия одинаково полезны для агента. К записям в буфере можно добавить веса, которые будут показывать насколько ценным для обучения нейросети был этот опыт [5]. Чем больше вес траектории, тем больше вероятность её выбора для обучения. Это позволяет чаще проигрывать полезный опыт и меньше выбирать бесполезный. Но как оценить накопленный опыт? Здесь нам и пригодится понятие TD-ошибки.
Абсолютная TD-ошибка, по сути, показывает насколько изменяется оценка Q-функции. Чем больше модуль TD-ошибки, тем большую корректировку мы провели, и тем больше мы обучились. Другими словами, мы хотим повторять тот опыт, который привел к заметной разнице между ожидаемой и реальной наградой, то есть заставил нейросеть многому научиться.
Если применить такой подход к примеру с бункером выше, то больший вес будет иметь опыт, когда агент сражался и побеждал – в этот момент мы дали новую оценку действию «сражаться» и получили высокую TD-ошибку. Этот опыт будет повторен многократно, и со временем у действия «сражаться» уже будет положительная ожидаемая награда. Если же агент спрячется в бункер, он не будет получать никакой новой информации. Была у действия награда 0 – осталась 0. Такому действию будет поставлен низкий приоритет во время воспроизведения опыта, потому что оно и так уже хорошо оценено.
Если внимательно посмотреть, то такой подход приближает нас к обучению с учителем. Теперь есть некоторый датасет (пусть и формирующийся динамически), на котором обучается нейросеть. Значит, появляется возможность использовать и преимущества обучения с учителем.
Ape-x
Агент собирает действия в буфер и независимо от этого обучается. Соответственно, задачу наполнения буфера и задачу обучения нейросети можно отделить друг от друга. Для этого была предложена архитектура Ape-x [6]. Нейросеть, используемую как функцию оценки ценности действия, назвали Learner, а агента, выполняющего действие в среде, назвали Actor. Очевидно, Actor может быть не один. Каждый Actor имеет свой собственный экземпляр окружающей среды, что позволяет накапливать опыт гораздо быстрее. Однако, все полученные траектории вида
Каждый Actor имеет нейросеть с одними и теми же весами, полученными из Learner. Learner учится постоянно, однако обновление нейросети в Actor происходит периодически, чтобы возможные скачки в поведении среды (возможно, вызванные шумом) не так сильно влияли на обучение.
Ниже представлена иллюстрация этой архитектуры:

R2D2
Experience replay хоть и хранит прошлые действия, но используется только для обучения нейросети. Решение о действии в состоянии все ещё принимается только на основе наблюдаемого состояния, без учета предыдущих. Хотелось бы добавить нейросети память для более точного описания среды в текущий момент, например, использовать рекуррентные нейронные сети (Recurrent Neural Network, RNN). Причем сделать это так, чтобы не потерять преимущества архитектуры Ape-X.
Здесь возникает проблема — нужно, чтобы наша RNN училась. Сейчас сохраненный опыт из буфера вытаскивается псевдослучайным образом (чаще выбираются действия с большим приоритетом), но из-за этого рушится порядок того, как среда отвечала на разные действия, а значит RNN не выявит никаких закономерностей и не обучится (это как если бы в задаче машинного перевода на вход нейросети подавалось не предложение в правильном порядке, а случайно перемешанные слова из этого предложения). Для решения этой проблемы была создана архитектура агента под названием Recurrent Replay Distributed DQN или R2D2 [2].
Для использования RNN будем хранить не отдельные шаги, а целые последовательности фиксированной длины, состоящие из идущих друг за другом траекторий
Встает вопрос, как во время обучения, при перескакивании с одной последовательности на другую (используется тот же подход Prioritized Experience Replay, но уже к траекториям) инициализировать скрытое состояние RNN?
Самая простая идея – инициализировать его нулями. Это не очень хорошо, так как нули не несут никакой информации. Можно попробовать хранить рядом с каждой траекторией скрытое состояние, которое образовалось при прошлом обучении на этой траектории. Это тоже не очень хороший подход, так как нейросеть обучается и сохраненное состояние может сильно отставать от создаваемого более поздней версией нейросети.
Для решения этой проблемы авторы статьи предлагают использовать Burn-in период. Давайте инициализируем состояние сначала нулями или прошлым состоянием, как описано выше, прогоним несколько траекторий из сохраненного опыта, не обучаясь, а затем начнем обучать нейросеть как обычно. За эти несколько пропущенных шагов скрытое состояние должно достаточно обновиться, и при этом RNN не учится на плохо инициализированных состояниях.
Рекуррентные сети позволили значительно улучшить эффективность агента.

Медианное значение очков относительно человека, набираемых агентом (средние очки человека – 100%) и время, затраченное на обучение в зависимости от архитектуры.
Выводы
Проследим проделанный путь. Для того, чтобы агенту принимать решение как действовать в данной ситуации, нужно дать оценку всем возможным действиям. Делать это с помощью таблицы возможно, но накладывает заметные ограничения. Из-за этого таблицу заменили нейросетью. Затем нейросети добавили буфер памяти, который позволяет избегать ситуаций, в которых агент взаимодействует лишь с частью окружающей среды – той, которую он непосредственно наблюдает сейчас. Некоторые записи в памяти ценнее для обучения, чем другие, поэтому было предложено расставлять им приоритеты. Задачи обучения и сбора информации о среде теперь разделимы, и можно отдельно собирать информацию в буфер, и отдельно обучать политику. После чего, не разрушая предыдущих наработок, в политику добавлен слой LSTM, который обучается благодаря тому, что в буфере хранятся сразу целые траектории и используется burn-in период.
В этой статье рассмотрены только вопросы, касающиеся буфера памяти и его разных модификаций. Например, в R2D2 ещё используется технология Double Q-learning, а Ape-X базируется на агенте Rainbow [7]. Rainbow, в свою очередь, является объединением нескольких способов улучшения Deep Q-learning. Для деталей лучше прочить оригинальную статью по Rainbow [7], а оттуда перейти к более детальному рассмотрению заинтересовавших «трюков» с deep Q-learning.
Пример работы
Реализация R2D2 существует во фреймворке Acme [8]. В качестве среды используем игру Time Pilot для приставки Atari 2600. Согласно графику из статьи [2], метод R2D2 в этой игре показывает себя лучше, чем Ape-X.

По оси ординат – среднее суммарное вознаграждение агента. По оси абсцисс – кол-во эпох. Оранжевая линия – R2D2, синяя – Ape-X, зеленая – R2D2 без RNN.
Обучим бота для этой игры. Цель – управляя синим самолетиком в центре экрана сбить вражеские желтые самолетики, и при этом не врезаться в них. Вот результат обучения на CPU в течении примерно двух суток:

Для обучения использована среда из библиотеки Gym [8]. Код для использования фреймворка Acme и среды Atatri 2600 можно посмотреть здесь [10]:
Ссылки
- S. Sutton, Andrew G. Barto, «Reinforcement Learning: An Introduction»
- Playing Atari with Deep Reinforcement Learning
- Recurrent Experience Replay in Distributed Reinforcement Learning
- Revisiting Fundamentals of Experience Replay
- Prioritized Experience Replay
- Distributed Prioritized Experience Replay
- Rainbow: Combining Improvements in Deep Reinforcement Learning
- Acme: a research framework for reinforcement learning
- Фреймворк Gym
- github.com/CyberLympha/ML-examples/blob/main/TimePilot.ipynb


dim2r
а формула (1) правильно записана ?
CyberLympha Автор
теперь правильно)
kantocoder
что возвращает функция argmax? Вы точно понимаете смысл уравнения Беллмана?
CyberLympha Автор
Большое спасибо, что заметили опечатку! Исправлено