Лямбда-исчисление — это язык программирования с единственным ключевым словом. Это асфальтовая топь Тьюринга, обнаруженная научным руководителем Тьюринга. В этом посте я расскажу о совершенно новой 397-байтной реализации двоичного лямбда-исчисления в виде Linux ELF для x86-64. Также в нём представлены удобно портируемый код на C и собранные двоичные файлы APE для других платформ.
SectorLambda реализует виртуальную машину Чёрча-Кривина-Тромпа с монадным вводом-выводом. В 397 байтах нам удалось реализовать сборку мусора, «ленивые» списки и хвостовую рекурсию. Интерпретатор извлекает самый младший бит из каждого байта stdin. Вывод состоит из байтов 0 и 1. Он 64-битный, однако смещение ограничено [0,255], поэтому программы не могут быть слишком большими. Поэтому это интересный инструмент для обучения, однако имеется 520-байтная версия для приложений более промышленного масштаба, обходящая многие подобные ограничения; впрочем, в ней нужно писать код ещё большей сложности.
-rwxr-xr-x 1 jart jart 397 Feb 27 12:15 blc-rw-r--r-- 1 jart jart 17K Feb 27 12:15 blc.SВиртуальную машину можно скомпилировать в Linux для Linux x64 следующим образом:
cc -c -o blc.o blc.Sld.bfd -o blc blc.o -T flat.ldsПрограмма считывается из stdin, за которым следует его ввод. Вот простой туториал по использованию функции тождественности (λ 0), в двоичном лямбда-исчислении кодируемой как (00 10):
$ { printf 0010; printf 0101; } | ./blc; echo
0101Если вы пользуетесь Mac, Windows, FreeBSD, NetBSD или OpenBSD, то можете вместо этого сделать следующее:
$ curl https://justine.lol/lambda/lambda.com >lambda.com
$ chmod +x lambda.com
$ { printf 0010; printf 0101; } | ./lambda.com; echo
0101Почему это важно
Программы, написанные на двоичном лямбда-исчислении, невероятно малы. Например, метациклический интерпретатор занимает всего 232 бита. Если работать с 8-битной версией интерпретатора (Blc с заглавной буквы), использующей истинный binary wire format, то мы можем получить представление о том, насколько малы могут быть программы, целевой платформой которых является виртуальная машина.
$ curl https://justine.lol/lambda/uni.Blc >uni.Blc
$ curl https://justine.lol/lambda/Blc >Blc
$ chmod +x Blc
$ { cat uni.Blc; printf ' '; printf 'hello world'; } | ./Blc; echo
hello world
$ ls -hal uni.Blc
-rw-r--r-- 1 jart jart 43 Feb 17 21:24 uni.BlcЭто означает, что наша 521-байтная виртуальная машина достаточно выразительна, чтобы реализовать себя всего в 43 байтах, то есть в меньше чем одной десятой от своего размера! Также в качестве виртуальной машины она имеет возможности, которых не хватает JVM, хотя и меньше неё на шесть порядков величин. Что-то подобное может иметь практическое применение в форматах сжатия, которым нужен маленький busy beaver, способный создавать большие объёмы данных. Кроме того, это просто круто.
Например, если вы собрали инструмент для сжатия, с его помощью можно закодировать файл как генерирующее его лямбда-выражение. Так как сложно внедрять новый формат сжатия, который не установлен у большинства людей, можно создать префикс сжатого файла с этим 397-байтным интерпретатором, получив автономный самораспаковывающийся архив, которым может пользоваться каждый. Кроме того, двоичное лямбда-исчисление будет более логичным в качестве встроенного микропроцессора, чем LISP.
Компиляция
Программы кодируются в следующем формате:
00 means abstraction (pops in the Krivine machine) 01 means application (push argument continuations) 1...0 means variable (with varint de Bruijn index)
Можно использовать шелл-скрипты sed в качестве компилятора байт-кода. Ему достаточно делать
s/λ/00/g, s/\[/01/g, s/[^01]//g и т. д.
#!/bin/sh</span>
tr \\n n |
sed '
s/;.*//
s/#.*//
s/1/⊤/g
s/0/⊥/g
s/λ/00/g
s/\[/01/g
s/9/11111111110/g
s/8/1111111110/g
s/7/111111110/g
s/6/11111110/g
s/5/1111110/g
s/4/111110/g
s/3/11110/g
s/2/1110/g
s/⊤/110/g
s/⊥/10/g
s/[^01]//g
'
Теперь мы можем писать более красивые программы:
{ printf %s "(λ 0)" | ./compile.sh
printf 00010101
} | ./blc
Программирование
Эта программа означает
exit(0), потому что она возвращает $nil или []:λ λλ0
Эта программа возвращает
[⊥,⊤] поэтому выводит 10.λ [[$pair $false] [[$pair $true] $nil]]
Эта программа означает
if (1 - 1 == 0) putc('1') else putc('0'):λ [[[$if [$iszero [[$sub $one] $one]]]
[[$pair $false] $nil]]
[[$pair $true] $nil]]
Эта программа делает то же самое, что и программа ident, но написана более обстоятельно. Среда выполнения передаёт два аргумента,
gro и put (или λ [[0 wr0] wr1]). Индекс 110 — это внешний параметр, а 10 — внутренний. То есть эта программа эквивалентна for (;;) putc(getc())λλ [1 0] ││ │└binds `put` or `(λ 0 wr0 wr1)` [cited as 0] └binds `gro` or `⋯` [cited as 1]
Эта программа инвертирует поток битов при помощи Y-комбинатора. Её скорость обработки составляет аж целых 16 кБ/с.
# a.k.a. Y(λfi.i(λbjn.❬¬b,fj❭)⊥)
[$Y λλ [[[$if 0] λλλ [[$pair [$not 2]] [4 1]]] $nil]]
││ │││
││ ││└consumes $nil terminator [uncited]
││ │└binds ???? input bit [cited as 1]
││ └binds (λ 0 ???? ⋯) [cited as 2]
│└binds gro (λ 0 ???? ⋯) [cited by first 0]
└binds recursive function [cited as 4]
Если вам нужно объяснение происходящего, то вы можете воспользоваться интерпретатором lambda.com с флагом
-r. Например, вот вышеприведённый код с пустым вводом. Вы можете наблюдать, как происходят разные действия, например, применение Y-комбинатора. Затем он считывает некий ввод, а затем использует бит ввода как предикат в условном операторе if. В отличие от LISP, лямбда-исчисление выполняет головную редукцию, поэтому можно считать, что блок вычислений лениво потребляет поток продолжений. Именно из-за всей этой парадигмы в языках наподобие Haskell не нужно так много скобок.$ nil="λλ 0" $ true="λλ 1" $ false="λλ 0" $ pair="λλλ [[0 2] 1]" $ not="λ [[0 $false] $true]" $ Y="λ [λ [1 [0 0]] λ [1 [0 0]]]" $ printf %s "[$Y λλ [[0 λλλ [[$pair [$not 2]] [4 1]]] $nil]]" | ./compile.sh | ./lambda.com -r [Y λλ [[0 λλλ [[pair [¬ 2]] [4 1]]] ⊥]] λ [0 put] [[Y λλ [[0 λλλ [[pair [¬ 2]] [4 1]]] ⊥]] ⋯] 0 put Y λλ [[0 λλλ [[pair [¬ 2]] [4 1]]] ⊥] ⋯ put λ [1 [0 0]] λ [1 [0 0]] ⋯ put 1 [0 0] ⋯ put λλ [[0 λλλ [[pair [¬ 2]] [4 1]]] ⊥] [0 0] ⋯ put λ [[0 λλλ [[pair [¬ 2]] [4 1]]] ⊥] ⋯ put 0 λλλ [[pair [¬ 2]] [4 1]] ⊥ put ⋯ λλλ [[pair [¬ 2]] [4 1]] ⊥ put ⊥ λλλ [[pair [¬ 2]] [4 1]] ⊥ put λ 0 ⊥ put 0 put ⊥ put λ 0
Эта программа означает
for x in reversed(stdin): put(x)# a.k.a. λa.a(ω(λbcde.d(bb)(λf.fce)))⊥ λ [[0 [λ [0 0] λλλλ [[1 [3 3]] λ [[0 3] 1]]]] $nil]
Эта программа означает
['1'] * 4**3. Если вам нужно возвести в степень бОльшие числа, например, 9**3 (по стандартам ФП это big data), тогда вам потребуется изменить параметр STACK в blc.S так, чтобы попросить у операционной системы чего-то большего, чем предоставляется по умолчанию.λ [[$Y λλ [[[$if [$iszero 0]]
$nil]
[[$pair $false]
[1 [$dec 0]]]]]
[[$pow $four] $three]]
Вот написанный на BLC интерпретатор BLC размером 232 бита.
[[λ [0 0]
λλλ [[[0 λλλλ [2 λ [[4 [2 λ [[1 [2 λλ [2 λ [[0 1] 2]]]]
[3 λ [3 λ [[2 0] [1 0]]]]]]]
[[0 [1 λ [0 1]]]
λ [[3 λ [3 λ [1 [0 3]]]] 4]]]]]
[2 2]] 1]]
λ [0 [λ [0 0] λ [0 0]]]]
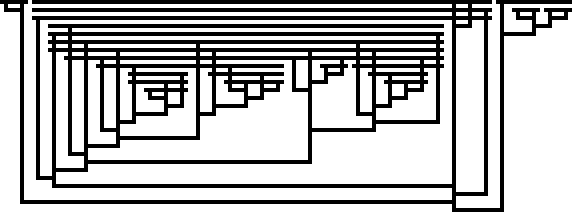
Вот генератор кривой Пеано гильбертова пространства с использованием 8-битной версии:
$ curl https://justine.lol/lambda/hilbert.Blc >hilbert.Blc
$ curl https://justine.lol/lambda/Blc >Blc
$ chmod +x Blc
$ { cat hilbert.Blc; printf 123; } | ./Blc
_ _ _ _
| |_| | | |_| |
|_ _| |_ _|
_| |_____| |_
| ___ ___ |
|_| _| |_ |_|
_ |_ _| _
| |___| |___| |
Определения
Вот некоторые важные значения:
nil="λλ0" false="λλ0" true="λλ1"
Вот некоторые важные абстракции:
if="λ 0" omega="λ [0 0]" pair="λλλ [[0 2] 1]" car="λ [0 $true]" cdr="λ [0 $false]" or="λλ [[0 0] 1]" and="λλ [[0 1] 0]" not="λλλ [[2 0] 1]" xor="λλ [[1 λλ [[2 0] 1]] 0]" bitxor="λλ [[1 0] λλ [[2 0] 1]]" iszero="λλλ [[2 λ 1] 1]" Y="λ [λ [0 0] λ [1 [0 0]]]"
Вот целочисленные значения:
zero="λλ 0" one="λλ [1 0]" two="λλ [1 [1 0]]" three="λλ [1 [1 [1 0]]]" four="λλ [1 [1 [1 [1 0]]]]" five="λλ [1 [1 [1 [1 [1 0]]]]]" six="λλ [1 [1 [1 [1 [1 [1 0]]]]]]" seven="λλ [1 [1 [1 [1 [1 [1 [1 0]]]]]]]" eight="λλ [1 [1 [1 [1 [1 [1 [1 [1 0]]]]]]]]" nine="λλ [1 [1 [1 [1 [1 [1 [1 [1 [1 0]]]]]]]]]"
Вот арифметика:
pow="λλ [0 1]" mul="λλλ [2 [1 0]]" dec="λλλ [[[2 λλ [0 [1 3]]] λ 1] λ 0]" sub="λλ [[0 $dec] 1]" inc="λλλ [1 [[2 1] 0]]" add="λλλλ [[3 1] [[2 1] 0]]" fac="λλ [[[1 λλ [0 [1 λλ [[2 1] [1 0]]]]] λ1] λ0]" min="λλλλ [[[3 λλ [0 1]] λ1] [[2 λλ [3 [0 1]]] λ1]]" div="λλλλ [[[3 λλ [0 1]] λ 1] [[3 λ [[[3 λλ [0 1]] λ [3 [0 1]]] λ0]] 0]]" mod="λλλλ [[[3 $cdr] [[3 λ [[[3 λλλ [[0 [2 [5 1]]] 1]] λ1] 1]] λ1]] λλ0]"
Вот предикаты:
eq="λλ [[[[1 λ [[0 λ0] λ0]] [[0 λλλ [1 2]] λλ0]] λλλ0] λλ1]" le="λλ [[[1 λλ [0 1]] λλλ1] [[0 λλ [0 1]] λλλ0]]" lt="λλ [[[0 λλ [0 1]] λλλ0] [[1 λλ [0 1]] λλλ1]]" odd="λ [λ [0 0] λλ [[0 λλ 1] λ [[0 λλ 0] [2 2]]]]" divides="λλ [[[1 $cdr] [$omega λ[[[1 λλλ [[0 [2 λλ0]] 1]] λ[1 1]] λλ1]]] λλ0]"
Инструментарий
Вот как используется утилита blcdump:
$ printf 0010 | blcdump.com -l 2>/dev/null λa.a # convert to traditional notation $ blcdump.com -l <invert.blc 2>/dev/null ω(λab.b(λcdef.f(c⊥⊤)(aad))⊥) # convert to de Bruijn notation $ blcdump.com <invert.blc 2>/dev/null [ω λλ [[0 λλλλ [[0 [[3 ⊥] ⊤]] [[5 5] 2]]] ⊥]] # convert Blc to blc $ blcdump.com -bB <uni.Blc 2>/dev/null 00011001010001101000000001010101100000000000010... # create portable lambda expression $ blcdump.com -lnNS <invert.blc 2>/dev/null (\a.a a) (\a.(\b.(b (\c.(\d.(\e.(\f.(f(c (\g.(\h.h)) (\g.(\h.g)))(a a d)))))) (\c.(\d.d)))))
Вот как используется утилита lam2bin:
$ { printf 'λa.a' | lam2bin.com; printf 1010; } | blc
1010
$ { printf '\\a.a' | lam2bin.com; printf 1010; } | blc
1010
$ { printf 'ω(λab.b(λcdef.f(c⊥⊤)(aad))⊥)' | lam2bin.com; printf 1010; } | blc
0101
Вот как используется утилита asc2bin:
$ { printf 'λa.a' | lam2bin.com | asc2bin.com; echo hello; } | Blc
hello
Среда выполнения
ВМ разворачивает программу при запуске следующим образом:
???? ⟶ [λ [0 λ [[0 wr0] wr1]] [???? ⋯]]
Условное обозначение ленивого списка редуцируется следующим образом:
⋯ ⟹ $nil ;; if eof / error ⋯ ⟹ λ [[0 $false] ⋯] ;; if ~getc() & 1 ⋯ ⟹ λ [[0 $true] ⋯] ;; if getc() & 1
Условные обозначения
wr0 и wr1 редуцируются следующим образом:wr0 ⟹ λ [0 λ [[0 wr0] wr1]] ;; w/ putc(0) side-effect wr1 ⟹ λ [0 λ [[0 wr0] wr1]] ;; w/ putc(1) side-effect
8-битная среда выполнения (Blc с заглавной) разворачивается при помощи списков big-endian. Например, пробел (0b00100000) будет выглядеть так:
λ [[0 λ [[0 ⊤] λ [[0 ⊥] λ [[0 ⊥] λ [[0 ⊤] λ [[0 ⊥] λ [[0 ⊤] λ [[0 ⊤] λ [[0 ⊤] ⊥]]]]]]]]] ⋯]
Двоичные файлы
-rwxr-xr-x 1 jart jart 397 Feb 27 12:15 blc (только linux x86-64)-rwxr-xr-x 1 jart jart 521 Feb 27 12:15 Blc (только linux x86-64)-rwxr-xr-x 1 jart jart 20K Feb 28 12:11 tromp.com (ioccc 2012)-rwxr-xr-x 1 jart jart 48K Feb 28 12:11 lambda.com (дружественный)-rwxr-xr-x 1 jart jart 36K Feb 28 12:11 blcdump.com-rwxr-xr-x 1 jart jart 40K Feb 28 12:11 bru2bin.com-rwxr-xr-x 1 jart jart 40K Feb 28 12:11 lam2bin.com-rwxr-xr-x 1 jart jart 20K Feb 28 12:11 asc2bin.comПрограммы
-rw-r--r-- 1 jart jart 84 Feb 27 12:54 invert.blc-rw-r--r-- 1 jart jart 167 Feb 27 12:52 primes.blc-rw-r--r-- 1 jart jart 232 Feb 27 12:52 uni.blc-rw-r--r-- 1 jart jart 43 Feb 27 12:52 uni.Blc-rw-r--r-- 1 jart jart 67 Feb 27 12:52 reverse.blc-rw-r--r-- 1 jart jart 9 Feb 27 12:52 reverse.Blc-rw-r--r-- 1 jart jart 186 Feb 27 12:52 symbolic.Blc-rw-r--r-- 1 jart jart 143 Feb 27 12:52 hilbert.Blc-rw-r--r-- 1 jart jart 141 Feb 27 12:52 parse.Blc-rw-r--r-- 1 jart jart 112 Feb 27 12:52 bf.Blc-rw-r--r-- 1 jart jart 112 Feb 27 12:55 hw.bfСкрипты
-rwxr-xr-x 1 jart jart 343 Feb 27 12:06 compile.sh-rwxr-xr-x 1 jart jart 224 Feb 27 12:06 trace.sh-rwxr-xr-x 1 jart jart 661 Feb 27 12:06 lam2sh.sh-rwxr-xr-x 1 jart jart 573 Feb 27 12:06 lam2sqr.sh-rwxr-xr-x 1 jart jart 565 Feb 27 12:06 sqr2lam.shИсходники
-rw-r--r-- 1 jart jart 17K Feb 27 12:15 blc.S-rw-r--r-- 1 jart jart 12K Feb 24 17:25 Blc.S-rw-r--r-- 1 jart jart 3.1K Feb 27 12:18 Makefile-rw-r--r-- 1 jart jart 1023 Feb 27 12:03 tromp.c-rw-r--r-- 1 jart jart 7.9K Feb 27 12:04 lambda.c-rw-r--r-- 1 jart jart 3.1K Feb 27 12:05 asc2bin.c-rw-r--r-- 1 jart jart 7.9K Feb 27 12:05 lam2bin.c-rw-r--r-- 1 jart jart 8.3K Feb 27 12:05 bru2bin.c-rw-r--r-- 1 jart jart 4.7K Feb 27 12:08 blcdump.c-rw-r--r-- 1 jart jart 1.3K Feb 27 12:05 blc.h-rw-r--r-- 1 jart jart 4.5K Feb 27 12:09 debug.c-rw-r--r-- 1 jart jart 2.2K Feb 27 12:09 error.c-rw-r--r-- 1 jart jart 2.4K Feb 27 12:09 getbit.c-rw-r--r-- 1 jart jart 7.9K Feb 27 12:04 lambda.c-rw-r--r-- 1 jart jart 1.8K Feb 27 12:10 needbit.c-rw-r--r-- 1 jart jart 2.5K Feb 27 12:08 parse.c-rw-r--r-- 1 jart jart 35K Feb 27 12:08 print.c-rw-r--r-- 1 jart jart 1023 Feb 27 12:03 tromp.c-rw-r--r-- 1 jart jart 2.5K Feb 27 12:10 vars.c-rw-r--r-- 1 jart jart 2.1K Mar 1 09:11 flat.lds-rw-r--r-- 1 jart jart 3.5K Mar 1 09:11 unflat.ldsПрозрачность DWARF
-rwxr-xr-x 1 jart jart 419K Feb 27 12:11 tromp.com.dbg-rwxr-xr-x 1 jart jart 822K Feb 27 12:11 lambda.com.dbg-rwxr-xr-x 1 jart jart 736K Feb 27 12:11 blcdump.com.dbg-rwxr-xr-x 1 jart jart 663K Feb 27 12:11 bru2bin.com.dbg-rwxr-xr-x 1 jart jart 677K Feb 27 12:11 lam2bin.com.dbgДемо Blinkenlights
Вот скринкаст работающей SectorLambda в Blinkenlights. Программа вводится в консоль как функция тождества 0010, или (λ 0), или λ????.????. После ввода программы все дальнейшие нажатия клавиш будут выводиться echo на основании младшего бита.
В правом нижнем углу видны распределения кучи в стеке, увеличивающемся в процессе сборки его списка. В правом верхнем углу видно увеличивающееся по мере считывания ввода количество неизменяемых членов. Эти члены записываются непосредственно после исполняемого образа.
Схемы процедур
busy beaverλa.(λb.bb)(a(λb.a)) λ [$omega [0 λ 1]] 000100011010011000110  ackermannλa.a(λbc.cbc)(λb.bb)a λ [[[0 λλ [[0 1] 0]] $omega] 0] 00010101100000010110110100001101010  Fibonacciλa.a(λbcd.bd(λe.c(de)))(λbc.b)(λb.b) 00010101100000000101111010000111 10011101000001100010  minimumλabcd.a(λef.fe)(λe.d)(b(λef.c(fe))(λe.d)) 000000000101011111000000110110001 100101111000000111110011011000110  reverse streamλa.a((λb.bb)(λbcde.d(bb)(λf.fce)))(λbc.c) λ [[0 [$omega
λλλλ [[1 [3 3]] λ [[0 3] 1]]]]
$nil]
0001011001000110100000000001011100 111110111100001011011110110000010  all predicateλa.(λb.bb)(λbc.c(λde.e)(bb)) λ [$omega λλ [[0 $false] [1 1]]] 00010001101000000101100000100111 0110  none predicateλa.(λb.bb)(λbc.c(λde.d)(bb)) 00010001101000000101100000110011 10110  less or equal predicateλab.a(λcd.dc)(λcde.d)(b(λcd.dc)(λcde.e)) 00000101011100000011011000000011 00101100000011011000000010  equal predicateλab.a(λc.c(λd.d)(λd.d))(b(λcde.dc)(λcd.d))(λcde.e)(λcd.c) 00000101010111000010110001000100 10110000000011101110000010000000 100000110 |
additionλabcd.ac(bcd) λλλλ [[3 1] [[2 1] 0]] 000000000101111101100101111011010  subtractionλab.b(λcde.c(λfg.g(fd))(λf.e)(λf.f))a λλ [[0 λλλ [[[2 λλ [0 [1 3]]]
λ 1] λ 0]] 1]
00000101100000000101011110000001 100111011110001100010110  factorialλab.a(λcd.d(c(λef.de(ef))))(λc.b)(λc.c) λλ [[[1 λλ [0 [1
λλ [[2 1] [1 0]]]]] λ 1]
λ 0]
00000101011100000011001110000001 0111101100111010001100010  invert bitstreamω(λab.b(λcdef.f(c⊥⊤)(aad))⊥) [$Y λλ [[[$if 0]
λλλ [[$pair [$not 2]]
[4 1]]]
$nil]]
01000110100000010110000000000101 10010111110000010000011001011111 11011111101110000010  even predicateλa.(λb.bb)(λbc.c(λde.e)(λd.d(λef.e)(bb))) 00010001101000000101100000100001 011000001100111101110  odd predicateλa.(λb.bb)(λbc.c(λde.d)(λd.d(λef.f)(bb))) 00010001101000000101100000110000 101100000100111101110  less than predicateλab.b(λcd.dc)(λcde.e)(a(λcd.dc)(λcde.d)) 00000101011000000110110000000100 10111000000110110000000110  quineλa.a((λb.bb)(λbcdef.fc(d(bb)e)))a 000101100100011010000000000001011 011110010111100111111011111011010 
|
division
λabcd.a(λef.fe)(λe.d)(a(λe.b(λfg.gf)(λf.c(fe))(λf.f))d)
λλλλ [[[3 λλ [0 1]] λ 1] [[3 λ [[[3 λλ [0 1]] λ [3 [0 1]]] λ 0]] 0]]
0000000001010111110000001101100011001011111000010101111100000011 01100001111100110110001010

modulus
λabcd.a(λe.e(λfg.f))(a(λe.b(λfgh.h(f(cg))g)(λf.e)d)(λe.d))(λef.f)
λλλλ [[[3 λ [0 λλ 1]] [[3 λ [[[3 λλλ [[0 [2 [5 1]]] 1]] λ 1] 1]] λ 1]] λλ 0]
0000000001010111110000110000011001011111000010101111100000000101 100111100111111101101100011011000110000010

divides predicate
λab.a(λc.c(λde.d))((λc.cc)(λc.b(λdef.f(d(λgh.h))e)(λd.cc)(λde.d)))(λcd.d)
0000010101110000110000011001000110100001010111000000001011001111 000001011000011101100000110000010

binary lambda calculus interpreter
(λa.aa)(λabc.c(λdefg.e(λh.d(f(λi.h(g(λjk.i(λl.lkj)))(f(λj.g(λk.ik(jk))))))(h(g(λi.ih))(λi.f(λj.g(λk.j(kh)))e))))(aa)b)(λa.a((λb.bb)(λb.bb)))
0101000110100000000101011000000000011110000101111110011110000101 1100111100000011110000101101101110011111000011111000010111101001 1101001011001110000110110000101111100001111100001110011011110111 1100111101110110000110010001101000011010
binary lambda calculus interpreter w/ byte i/o
λa.a((λb.bb)(λb.(λcde.e(λfgh.g(λijk.(λl.f(c(λm.i(l(λno.m(λp.pon)))(c(λn.l(λo.mo(no)))))j)(i(l(λm.mi)j)(c(λm.l(λn.m(ni)))g)))d)(λi.i(λj.cd(λk.kfj))))(λf.f(cd)))(bb))(λbc.b((λd.dd)(λd.dd))))
0001100101000110100001000000010110000000010111000000001000101111 1111001011111111111000010111111001110000001111000010110110111001 1111111111100001111000010111101001110101110010111110010110000110 1111101110010111111111110000111000011100110111111011111101111111 1000011000010111111111011111110000101101111110110000110011111011 10011010000001110010001101000011010

Goldbach
(λa.a((λb.bb)(λbcd.(λef.ae(f(bbe)))(λe.eed(λf.fc)e))(λbcde.e)))((λa.aa)(λabc.c(λde.e)((λd.aad((λe.ee)(λe.d(ee))))(λd.(λe.e(e(bd)))(λefgh.hf(ge)))))(λabcd.d(λef.e)(ca)))
0100011001010001101000000001000001011111110110011001011111101111 1011000010101011010110000110111101000000000100101000110100000000 1011000001001000101011111011110100100011010000111001101000010001 1001100111110110000000000101101110011101111000000000010110000011 00111011110

Goodstein
λa.a(λbcd.b(λe.c(λfg.e(λhij.jh(if))(λh.g)(λhi.i)))(λef.de(d(λg.e(λhij.g(cdi(λkl.j(λm.mkl))(λkl.j(λm.kml))h)ij))f)))(λb.b)(λb.b(λcd.c)(λc.c))(λb.b(λcde.c))(λb.b)(λbc.b(λde.cd(de)))(λbc.b(λde.cd(d(de)))c)(λb.b)
0001010101010101011000000001011110000111100000010101111000000001 0110111001110111110001100000100000010111101100101111000011110000 0000101011111001010101011111111101111111011000000111100001011011 1011000000111100001011110101101110110101000100001011000001100010 0001100000001110001000000111000000101111011001110100000010111000 0001011110110011100111010100010

primes
λa.(λb.(λc.b(b((λd.dd)(λdef.f(λgh.h)((λg.ddg((λh.hh)(λh.g(hh))))(λghij.jh(i(eg)))))(λdef.b(fd))))((λde.d(d(de)))(ccc)(λdefg.ge(fd))(λdefg.g)))(λcd.c(cd)))(λbc.c(λde.d)b)
0001000100010111001110010100011010000000010110000010010001010111 1101111010010001101000011100110100000000001011011100111001111111 0111100000000111111001101110010101000001110011100111010010110101 0000000000101101110011101111000000000100000011100111010000001011 00000110110

sort
λa.(λb.bb)(λb.(λcde.e(λfg.(λh.hh)(λhi.i(λjkl.hhk(λm.j(λnopqrs.sm(n(λu.uoq)q)(nr(λu.uor)))(λnop.p(λqr.mq(λs.sqr))no)))(λj.(λk.jkkk)(λkl.l)))e(λhijk.(λl.h(d(λmn.n))(c(l(λmn.m))i(c(l(λmn.n))jk)))(λlm.d(λn.nlm)))))(bb))(λb.b)a(λbc.c)
0001010101000110100001000000011000000101010001101000000101100000 0001010111111011111011000010111110000000000000010101101111111001 0111111100001011011111101111011100101111111011000010110111111011 1000000001010110000001011111110110000101101110110111011000010001 0101110101010000010111000000000010001011111100111111111100000100 1010111111111110011000001101111001010111111111110011000001011101 1000000111111111110000101101110110011010001010000010

compliant brainf#*k interpreter
λa.(λb.a((λc.cc)(λc.(λd.(λe.(λf.(λg.(λh.g(f(h(f(h(f(h(h(e(b(λijk.ikj)))))(f(f(e(λijklm.m(λn.inkl)))(e(b(λi.i))))(g(e(λijklmn.nj(ijklm)))))))(h(h(f(g(e(λijkl.l(λm.im(λn.njk)))))(g(e(λijkl.ki(λm.mjl)))))))))(g(h(h(f(h(h(λij.jd(λk.e((λl.ll)(λlmn.n((λo.oo)(λopq.p(q(oo))(λr.k(llr))))mn))k))))(g(h(λijk.k(λl.l)j)))))))))(f(e(λh.h))))(λg.fg(e(λh.h))))(λfgh.h(λi.ifg)))(λefg.gd(λhij.j(λk.e(hk))i)))(cc)))(λc.(λd.dd)(λde.e((λf.f(f(f(λgh.h(λij.i)g))))(λfg.f(fg))(λfg.g))(dd))(c(λdefghi.i))c))(λbcd.c((λe.ee)(λefg.f(λhij.eei(λkl.g(λm.m(lh)k)(bhl(λm.m))))(gf(λhij.hji)))d(λef.e)))
0001000101110010001101000010001000100010001000111001011110011001 0111100110010111100110011001111100111111110000000010111101011001 0111100101111001111100000000000011000010101111111010111101110011 1110011111111000100111001111100000000000000101101111100101010111 1111011111011110111011001100110010111100111001111100000000001100 0010111111010000101101111101111001110011111000000000010111011110 0001011011110110011100110011001011110011001100000010110111111100 0010111111110010001101000000001010110010001101000000001011100110 0111101110000111111111001011111111011111110101101010011100110000 0000101100010110011100111100010000101110100111100010000000011000 0101101111011100000000101101111000000001011000011111111001111101 0110011010000101010001101000000101100101000110011001100000010110 0000110110000001110011101000001001110110011000000000000010100000 0001110010101000110100000000101110000000010101111111011111101100 0000101111111000010110011101111110111001010111111111111011111010 00100101101100000000101111010110100000110

Как это работает
#define IOP 0 // code for gro, wr0, wr1, put
#define VAR 1 // code for variable lookup
#define APP 2 // code for applications
#define ABS 3 // code for abstractions
#define REF(c) (++(c)->refs, c)
struct Parse {
int n;
int i;
};
struct Closure {
struct Closure *next;
struct Closure *envp;
int refs;
int term;
};
static const char kRom[] = {
APP, 0, // 0 (λ 0 λ 0 (λ 0 wr0 wr1) put) (main gro)
ABS, // 2 λ 0 λ 0 (λ 0 wr0 wr1) put
APP, 0, // 3
VAR, 0, // 5
ABS, // 7
APP, // 8
ABS, // 9 λ 0 λ 0 wr0 wr1
APP, 2, // 10
VAR, // 12
IOP, // 13
ABS, // 14 λ 0 wr0 wr1
APP, 4, // 15
APP, 1, // 17
VAR, // 19
IOP, // 20 wr0
IOP, 0, // 21 wr1
};
long ip; // instruction pointer
long end; // end of code pointer
int mem[TERMS]; // bss memory for terms
struct Closure *frep; // freed closures list
struct Closure *contp; // continuations stack
struct Closure root = {.refs = 1};
struct Closure *envp = &root;
void Gc(struct Closure *p) {
for (; p && p != &root; p = p->envp) {
if (--p->refs) break;
Gc(p->next);
p->next = frep;
frep = p;
}
}
void Var(void) {
int i, x;
struct Closure *t, *e;
e = t = envp;
x = mem[ip + 1];
for (i = 0; i < x && e != &root; ++i) e = e->next;
if (e == &root) Error(10 + x, "UNDEFINED VARIABLE %d", x);
ip = e->term;
envp = REF(e->envp);
Gc(t);
}
void Gro(void) {
int c;
if ((c = fgetc(stdin)) != -1) {
mem[end++] = ABS;
mem[end++] = APP;
mem[end++] = 8;
mem[end++] = APP;
mem[end++] = 2;
mem[end++] = VAR;
mem[end++] = 0;
mem[end++] = ABS;
mem[end++] = ABS;
mem[end++] = VAR;
mem[end++] = ~c & 1;
} else {
mem[end++] = ABS;
mem[end++] = ABS;
mem[end++] = VAR;
mem[end++] = 0;
}
}
void Put(void) {
fputc('0' + (ip & 1), stdout);
ip = 2;
}
void Bye(void) {
int rc = mem[ip + 2]; // (λ 0) [exitcode]
if (rc) Error(rc, "CONTINUATIONS EXHAUSTED");
if (postdump && !rc) Dump(0, end, stderr);
exit(0);
}
// pops continuation and pushes it to environment
void Abs(void) {
if (!contp) Bye();
struct Closure *t = contp;
contp = t->next;
t->next = envp;
envp = t;
++ip;
}
struct Closure *Alloc(void) {
struct Closure *t;
if (!(t = frep)) {
if (!(t = calloc(1, sizeof(struct Closure)))) {
Error(6, "OUT OF HEAP");
}
}
frep = t->next;
t->refs = 1;
++heap;
return t;
}
// pushes continuation for argument
void App(void) {
int x = mem[ip + 1];
struct Closure *t = Alloc();
t->term = ip + 2 + x;
t->envp = t->term > 21 && t->term != end ? REF(envp) : &root;
t->next = contp;
contp = t;
ip += 2;
}
void Iop(void) {
if (ip == end) {
Gro();
} else {
Put(); // ip ∈ {6,13,20,21}
}
Gc(envp);
envp = &root;
}
static void Rex(void) {
switch (mem[ip]) {
case VAR:
Var();
break;
case APP:
App();
break;
case ABS:
Abs();
break;
case IOP:
Iop();
break;
default:
Error(7, "CORRUPT TERM");
}
}
char GetBit(FILE* f) {
int c;
if ((c = fgetc(f)) != -1) c &= 1;
return c;
}
char NeedBit(FILE* f) {
char b = GetBit(f);
if (b == -1) Error(9, "UNEXPECTED EOF");
return b;
}
struct Parse Parse(int ignored, FILE* f) {
int t, start;
char bit, need;
struct Parse p;
for (need = 0, start = end;;) {
if (end + 2 > TERMS) Error(5, "OUT OF TERMS");
if ((bit = GetBit(f)) == -1) {
if (!need) break;
Error(9, "UNFINISHED EXPRESSION");
} else if (bit) {
for (t = 0; NeedBit(f);) ++t;
mem[end++] = VAR;
mem[end++] = t;
break;
} else if (NeedBit(f)) {
t = end;
end += 2;
mem[t] = APP;
p = Parse(0, f);
mem[t + 1] = p.n;
need = 1;
} else {
mem[end++] = ABS;
}
}
p.i = start;
p.n = end - start;
return p;
}
void LoadRom(void) {
long i;
for (; end < sizeof(kRom) / sizeof(*kRom); ++end) {
mem[end] = kRom[end];
}
mem[4] = 9;
mem[1] = end - 2;
}
void Krivine(void) {
int main;
long gotoget;
LoadRom();
mem[end++] = APP;
gotoget = end++;
main = end;
mem[gotoget] = Parse(1, stdin).n;
for (;;) Rex();
}Ассемблерный код
GAS LISTING o/blc.i page 1
GNU assembler version 2.34 (x86_64-alpine-linux-musl)
using BFD version (GNU Binutils) 2.34.
options passed : -aghlms=o/blc.lst
input file : o/blc.i
output file : o/blc.o
target : x86_64-alpine-linux-musl
time stamp : 2022-02-28T10:37:17.000-0800GAS LISTING o/blc.i page 2
1 /*-*- mode:unix-assembly; indent-tabs-mode:t; tab-width:8; coding:utf-8 -*-│
2 │vi: set et ft=asm ts=8 tw=8 fenc=utf-8 :vi│
3 ╞══════════════════════════════════════════════════════════════════════════════╡
4 │ Copyright 2022 Justine Alexandra Roberts Tunney │
5 │ │
6 │ Permission to use, copy, modify, and/or distribute this software for │
7 │ any purpose with or without fee is hereby granted, provided that the │
8 │ above copyright notice and this permission notice appear in all copies. │
9 │ │
10 │ THE SOFTWARE IS PROVIDED "AS IS" AND THE AUTHOR DISCLAIMS ALL │
11 │ WARRANTIES WITH REGARD TO THIS SOFTWARE INCLUDING ALL IMPLIED │
12 │ WARRANTIES OF MERCHANTABILITY AND FITNESS. IN NO EVENT SHALL THE │
13 │ AUTHOR BE LIABLE FOR ANY SPECIAL, DIRECT, INDIRECT, OR CONSEQUENTIAL │
14 │ DAMAGES OR ANY DAMAGES WHATSOEVER RESULTING FROM LOSS OF USE, DATA OR │
15 │ PROFITS, WHETHER IN AN ACTION OF CONTRACT, NEGLIGENCE OR OTHER │
16 │ TORTIOUS ACTION, ARISING OUT OF OR IN CONNECTION WITH THE USE OR │
17 │ PERFORMANCE OF THIS SOFTWARE. │
18 ╚─────────────────────────────────────────────────────────────────────────────*/
19
20 #define TRACE 0 // enable ./trace.sh support
21 #define FASTR 0 // favor perf over tininess
22 #define TERMS 5000000 // number of words of bss
23 #define STACK 0 // bytes of stack to get
24
25 #define IOP 0 // code for read, write0, write1, flush
26 #define VAR 1 // code for variable name lookup
27 #define APP 2 // code for applications
28 #define ABS 3 // code for abstractions
29
30 #define NEXT 0*8
31 #define ENVP 1*8
32 #define REFS 2*8+0
33 #define TERM 2*8+4
34
35 #define mem %rbx
36 #define memd %ebx
37 #define envp %rbp
38 #define contp %r9
39 #define frep %r8
40 #define eof %r13
41 #define eofb %r13b
42 #define eofd %r13d
43 #define idx %r15
44 #define idxb %r15b
45 #define idxd %r15d
46
47 .macro pushpop constexpr:req register:req
48 .byte 0x6a,\constexpr
49 pop %r\register
50 .endm
51
52 .macro mxchg register:req memory:req
53 #if FASTRGAS LISTING o/blc.i page 3
54 mov \register,%rax
55 mov \memory,\register
56 mov %rax,\memory
57 #else
58 xchg \register,\memory
59 #endif
60 .endm
61
62 .bss
63 0000 00000000 .zero TERMS
63 00000000
63 00000000
63 00000000
63 00000000
64 .previous
65
66 0000 7F454C46 ehdr: .ascii "\177ELF"
67
68 ////////////////////////////////////////////////////////////////////////////////
69 // TWELVE BYTE OVERLAP #
70 // .byte 2 # EI_CLASS is ELFCLASS64
71 // .byte 1 # EI_DATA is ELFDATA2LSB
72 // .byte 1 # EI_VERSION is 1
73 // .byte 3 # EI_OSABI is ELFOSABI_LINUX
74 // .quad 0 #
75 0004 03 kRom1: .byte ABS # 0 (λ ((0 (λ (λ ?))) ⋯))
76 0005 02 .byte APP # 1 8
77 0006 08 .byte 8 #──2──┐ -
78 0007 02 .byte APP # 3 │ (0 (λ (λ ?)))
79 0008 02 .byte 2 #──4────┐ (read (λ (λ ?)))
80 0009 01 .byte VAR # 5 │ │ 0
81 000a 00 .byte 0 # 6 │ │ read
82 000b 03 .byte ABS #──7────┘ (λ (λ ?))
83 000c 03 .byte ABS # 8 │ (λ ?)
84 000d 01 .byte VAR # 9 ┴ ?
85 000e 00 .byte 0 # exit(0) %al
86 000f 00 .byte 0 # elf padding [mark]
87 ////////////////////////////////////////////////////////////////////////////////
88
89 0010 0200 ehdr2: .word 2 # e_type is ET_EXEC [precious]
90 0012 3E00 .word 62 # e_machine is EM_X86_64 [precious]
91
92 ////////////////////////////////////////////////////////////////////////////////
93 // FOUR BYTE OVERLAP #
94 // .long 1 # e_version is 1 [mark]
95 0014 58 Bye2: pop %rax # __NR_exit
96 0015 0F05 syscall #
97 0017 00 .byte 0 # elf padding
98 ////////////////////////////////////////////////////////////////////////////////
99
100 0018 00000000 ehdr3: .quad _start # e_entry [precious]
100 00000000
101 0020 38000000 .quad phdrs - ehdr # e_phoff is 56 [precious]
101 00000000
102
103 ////////////////////////////////////////////////////////////////////////////////
104 // FOURTEEN BYTE OVERLAP #GAS LISTING o/blc.i page 4
105 // .quad 0xc681c031 # e_shoff [should be 0] [mark]
106 // .long 0xfce2abac # e_flags [should be 0] [mark]
107 // .word 0xc3 # e_ehsize [should be 64] [mark]
108 0028 57 Get: push %rdi #
109 0029 31C0 xor %eax,%eax # __NR_read
110 002b 31FF xor %edi,%edi # stdin
111 002d 8D73FF lea -1(mem),%esi # buf
112 0030 0F05 syscall #
113 0032 EB1C jmp Get2 #
114 0034 00 .byte 0 # elf padding
115 0035 00 .byte 0 # elf padding
116 ////////////////////////////////////////////////////////////////////////////////
117
118 0036 3800 .word 56 # e_phentsize [precious]
119
120 ////////////////////////////////////////////////////////////////////////////////
121 // EIGHT BYTE OVERLAP #
122 // .word 1 # e_phnum [correct overlap]
123 // .word 0 # e_shentsize [correct overlap]
124 // .word 1|2|4 # e_shnum [p_flags clobber]
125 // .word 0 # e_shstrndx [correct overlap]
126 0038 01000000 phdrs: .long 1 # p_type is PT_LOAD
127 003c 07000000 .long 1|2|4 # p_flags is PF_X|PF_W|PF_R
128 ////////////////////////////////////////////////////////////////////////////////
129
130 0040 00000000 .quad 0 # p_offset [precious]
130 00000000
131 0048 00000000 .quad ehdr # p_vaddr [precious]
131 00000000
132
133 ////////////////////////////////////////////////////////////////////////////////
134 // EIGHT BYTE OVERLAP #
135 // .quad ehdr # p_paddr [mark]
136 0050 2016 Get2: and %dl,(%rsi) # 1. al= 1 (si)='0' → ZF=1 CF=1 EAX=0
137 0052 2816 sub %dl,(%rsi) # 2. al= 1 (si)='1' → ZF=1 CF=0 EAX=0
138 0054 FFC8 dec %eax # 3. al= 0 (si)=??? → ZF=0 CF=? EAX<0
139 0056 5F pop %rdi # 4. al=-1 (si)=??? → ZF=0 CF=? EAX<0
140 0057 C3 .Lret: ret #
141 ////////////////////////////////////////////////////////////////////////////////
142
143 0058 00000000 phdrs2: .quad filesz # p_filesz [insurmountable gulf]
143 00000000
144 0060 00000000 .quad memsz # p_memsz [insurmountable gulf]
144 00000000
145 // .quad 4096 # p_align
146
147 0068 97 Bye: xchg %edi,%eax
148 0069 C1EF10 shr $16,%edi
149 006c 6A3C push $60 # __NR_exit
150 006e EBA4 jmp Bye2
151
152 0070 FF4810 Gc: decl REFS(%rax) # unref memory (order matters)
153 0073 75E2 jnz .Lret # 1. free parents via recursion
154 0075 50 push %rax # 2. free self
155 0076 488B00 mov NEXT(%rax),%rax # 3. free siblings via iteration
156 0079 E8F2FFFF call Gc
156 FFGAS LISTING o/blc.i page 5
157 007e 58 pop %rax
158 007f 4C8900 mov frep,NEXT(%rax)
159 0082 4989C0 mov %rax,frep
160 0085 488B4008 mov ENVP(%rax),%rax
161 0089 EBE5 jmp Gc
162
163 008b 57 Parse: push %rdi # save 1
164 008c B0 0: .byte 0xB0 # lda §movsb,%al (nop next byte)
165 008d A4 1: movsb # 00 is abstraction
166 008e 41FFD6 call *%r14 # Get
167 0091 7314 jnc 2f
168 0093 41FFD6 call *%r14 # Get
169 0096 72F5 jc 1b
170 0098 B002 1: mov $APP,%al # 01 is application
171 009a AA stosb
172 009b 57 push %rdi # save 2
173 009c AE scasb
174 009d E8E9FFFF call Parse
174 FF
175 00a2 5E pop %rsi # rest 2
176 00a3 8806 mov %al,(%rsi)
177 00a5 EBE5 jmp 0b
178 00a7 B001 2: mov $VAR,%al # 1⋯ is variable
179 00a9 AA stosb # 0-based de Bruijn indices
180 00aa F6D8 neg %al
181 00ac FEC0 3: inc %al
182 00ae 50 push %rax
183 00af 41FFD6 call *%r14 # Get
184 00b2 58 pop %rax
185 00b3 73F7 jnc 3b
186 00b5 AA stosb
187 00b6 5E pop %rsi # rest 1
188 00b7 89F8 mov %edi,%eax
189 00b9 29F0 sub %esi,%eax
190 00bb C3 ret
191
192 00bc 55 Var: push envp
193 00bd 3D .byte 0x3D # cmp §0x6D8B48,%eax (nop 4x)
194 00be 488B6D00 1: mov NEXT(envp),envp
195 00c2 FFC9 dec %ecx
196 00c4 79F8 jns 1b
197 00c6 448B7D14 2: mov TERM(envp),idxd
198 00ca 488B6D08 mov ENVP(envp),envp
199 00ce FF4510 incl REFS(envp)
200 00d1 58 pop %rax
201 00d2 E899FFFF call Gc
201 FF
202 00d7 EB41 jmp Rex
203
204 00d9 4D85C9 Abs: test contp,contp
205 00dc 748A jz Bye
206 mxchg envp,NEXT(contp)
206 >
206 >
206 >
206 >
206 >GAS LISTING o/blc.i page 6
206 00de 498729 > xchg %rbp,0*8(%r9)
206 >
207 00e1 4987E9 xchg envp,contp
208 00e4 EB34 jmp Rex
209
210 00e6 41FFD6 Gro: call *%r14 # Get
211 pushpop 10,cx
211 00e9 6A0A > .byte 0x6a,10
211 00eb 59 > pop %rcx
212 00ec BE000000 mov $kRom1,%esi
212 00
213 00f1 7403 jz 2f
214 00f3 83C607 add $7,%esi
215 00f6 B000 2: mov $0,%al
216 00f8 1400 adc $0,%al
217 00fa F3A4 rep movsb
218 00fc AA stosb
219 00fd EB1B jmp Rex
220
221 _start:
222 #if STACK
223 mov $STACK,%rsi
224 mov $9,%al # __NR_mmap
225 mov $3,%dl # PROT_READ|PROT_WRITE
226 mov $0x0122,%r10w # MAP_PRIVATE|MAP_ANONYMOUS|MAP_GROWSDOWN
227 syscall
228 lea -24(%rax,%rsi),%rsp
229 mov $0,%dl
230 #endif
231 00ff BB000000 mov $kRom,memd # romz
231 00
232 0104 41BE0000 mov $Get,%r14d # saves two bytes
232 0000
233 010a 4889E5 mov %rsp,envp # prevent segfaults clobber argv[0]
234 010d FEC2 inc %dl # dx=1 for read() and write()
235 010f 8D7B16 .byte 0x8d,0x7b,kEnd-kRom+1 # lea kEnd-kRom+1(mem),%edi
236 0112 E874FFFF call Parse # parse expr (xxx: tight displacement)
236 FF
237 0117 884315 .byte 136,67,kEnd-kRom # mov %al,kEnd-kRom(mem)
238 // jmp Rex # sets main() apply length
239
240 011a 428B043B Rex: mov (mem,idx),%eax # head normal form reduction
241 011e 0FB6CC movzbl %ah,%ecx # %al should be ∈ {0,1,2,3}
242 0121 41FFC7 inc idxd
243 0124 3C02 cmp $APP,%al
244 0126 77B1 ja Abs
245 0128 7423 je App
246 012a 84C0 test %al,%al
247 012c 758E jnz Var
248 // jmp Iop
249
250 012e 41FFCF Iop: dec idxd # lazy lists like haskell
251 0131 4183FF15 cmp $21,idxd # length of rom
252 0135 77AF ja Gro
253 // jmp Put
254
255 0137 89DE Put: mov memd,%esiGAS LISTING o/blc.i page 7
256 0139 4183C71E add $30,idxd # 18,19 += 48,49 or '0','1'
257 013d 44883E mov idxb,(%rsi)
258 0140 41B707 mov $7,idxb # λ 0 λ 0 wr0 wr1
259 0143 57 push %rdi
260 0144 89D7 mov %edx,%edi # stdout
261 0146 89D0 mov %edx,%eax # __NR_write
262 0148 0F05 syscall
263 014a 5F pop %rdi
264 014b EBCD jmp Rex
265
266 014d 4D85C0 App: test frep,frep
267 0150 7508 jnz 1f
268 0152 31C0 xor %eax,%eax
269 0154 50 push %rax # calloc() on stack lool
270 0155 50 push %rax
271 0156 50 push %rax
272 0157 4989E0 mov %rsp,frep
273 015a 41FFC7 1: inc idxd
274 mxchg contp,NEXT(frep) # get closure from free list
274 >
274 >
274 >
274 >
274 >
274 015d 4D8708 > xchg %r9,0*8(%r8)
274 >
275 0160 4D87C8 xchg contp,frep
276 0163 41FF4110 incl REFS(contp) # save machine state
277 0167 FF4510 incl REFS(envp)
278 016a 49896908 mov envp,ENVP(contp)
279 016e 4401F9 add idxd,%ecx
280 0171 41894914 mov %ecx,TERM(contp)
281 0175 EBA3 jmp Rex
282
283 0177 00 buf: .byte 0
284 0178 02 kRom: .byte APP # 0 [λ [0 λ [[0 wr0] wr1]] [main ⋯]]
285 0179 12 .byte .Lloop-1f #──1─┐
286 017a 03 1: .byte ABS # 2 │ λ [0 λ [[0 wr0] wr1]]
287 017b 02 .byte APP # 3 │ [0 λ [[0 wr0] wr1]]
288 017c 07 .byte .Lw01-1f #──4───┐
289 017d 0100 1: .byte VAR,0 # 5 │ │ 0
290 017f 03 .L0w01: .byte ABS #──7─┴─┘ λ [[0 wr0] wr1]
291 0180 02 .byte APP # 8 │ [[0 wr0] wr1]
292 0181 04 .byte 4 #─ 9───┐
293 0182 02 .byte APP # 10 │ │ [0 wr0]
294 0183 01 .byte 1 #─11─────┐ 1
295 0184 01 .byte VAR # 12 │ │ │ 0
296 0185 00 .Lwr: .byte IOP #─13─────┘ wr0
297 0186 00 .byte IOP #─14───┘ wr1
298 0187 02 .Lloop: .byte APP #─15─┘ [main ⋯]
299 kEnd:
300 GAS LISTING o/blc.i page 8
300 .globl ehdr
301 .globl _start
302 .type kRom,@object
303 .type kRom1,@object
304 .type ehdr,@object
305 .type ehdr2,@object
306 .type ehdr3,@object
307 .type phdrs,@object
308 .type phdrs2,@object
309 .type buf,@object
310 .weak filesz
311 .weak memszGAS LISTING o/blc.i page 9
DEFINED SYMBOLS
blc.S:66 .text:0000000000000000 ehdr
blc.S:75 .text:0000000000000004 kRom1
blc.S:89 .text:0000000000000010 ehdr2
blc.S:95 .text:0000000000000014 Bye2
blc.S:100 .text:0000000000000018 ehdr3
blc.S:221 .text:00000000000000ff _start
blc.S:126 .text:0000000000000038 phdrs
blc.S:108 .text:0000000000000028 Get
blc.S:136 .text:0000000000000050 Get2
blc.S:143 .text:0000000000000058 phdrs2
blc.S:147 .text:0000000000000068 Bye
blc.S:152 .text:0000000000000070 Gc
blc.S:163 .text:000000000000008b Parse
blc.S:192 .text:00000000000000bc Var
blc.S:240 .text:000000000000011a Rex
blc.S:204 .text:00000000000000d9 Abs
blc.S:210 .text:00000000000000e6 Gro
blc.S:284 .text:0000000000000178 kRom
blc.S:304 .text:000000000000018d kEnd
blc.S:266 .text:000000000000014d App
blc.S:250 .text:000000000000012e Iop
blc.S:255 .text:0000000000000137 Put
blc.S:283 .text:0000000000000177 buf
UNDEFINED SYMBOLS
filesz
memszАвторство
SectorLambda написан Жюстин Танни на основании криптограмм и обфусцированного кода, выпущенного Джоном Тромпом. Питер Ферье из Amazon внёс оптимизации размера.
Дополнительная информация
Комментарии (10)

wAgo
15.03.2022 11:16+7Волшебная фиговина - непонятно зачем нужная, но завораживает в желании понять что это такое )))

Druj
15.03.2022 14:02Подскажите что за отладчик на видео с демкой.

Healer
17.03.2022 12:50В оригинальной статье есть ссылка на отладчик https://justine.lol/blinkenlights/

AlexSpaizNet
15.03.2022 16:52Жесть конечно. Даже не представляю где человеку который этим занимается будет не скучно работать... апишки там пилить с микросервисами, с браузером бадаться =))

Olevin84
16.03.2022 09:47+1Ну, случается там компиляторы (интерпретаторы, виртуальные машины) всякие разрабатывать.
Новые языки программирования опять-же — нет-нет да появляются.
"Узок круг этих революционеров. Страшно далеки они от народа" (В.И.Ленин).

v1000
16.03.2022 00:05+5реализует виртуальную машину Чёрча-Кривина-Тромпа с монадным вводом-выводом.
Для неподготовленного человека это, наверное, звучит как текст из научной фантастики середины прошлого века.


palyaros02
Сложно, непонятно, но очень интересно