Структурные преобразования систем автоматического регулирования / forpes.ru

Главная
Структурные преобразования систем автоматического регулирования

Структурные преобразования систем автоматического регулирования +3

28.03.2022 00:20

petuhoff 2 1400 Источник

Для решения задач расчета и моделирования систем автоматического регулирования зачастую приходится рассматривать достаточно сложные системы, состоящие из множества звеньев (передаточных функций). Так, например, поворот закрылок у самолета обеспечивается следующим набором механизмов:

Два электродвигателя постоянного тока, каждый из которых имеет по четыре обмотки возбуждения (две последовательные и две параллельные).
Электромагнитные муфты сцепления-торможения.
Планетарный редуктор с суммирующей дифференциальной передачей.

И это только для обеспечения механизма поворота! Так же нужно учитывать, что до электродвигателей существует непосредственно система автоматического регулирования, которая вырабатывает необходимые сигналы управления. На рисунке 1. приведена структурная схема системы управления двигателем с постоянными магнитами. При этом в качестве входа в эту систему используется значение заданного положения, которое, в свою очередь, тоже должно быть определено исходя из решения уравнений динамики летательного аппарата.

Рисунок 1. Структурная схема управления двигателем с постоянными магнитами

При прямом физическом моделировании подобных систем приходится выполнять множество математических вычислений, и скорость вычислений снижается до неприемлемого уровня. Если мы хотим исследовать движение летательного аппарата в целом, необходимо представить модель сложной системы в упрощенном виде, желательно, не теряя качества и сохраняя необходимую точность. В предыдущей лекции при выводе уравнений динамики ядерного реактора мы показывали, каким образом, пренебрегая малыми величинами, мы получаем компактное выражение, и сохраняем точность в заданном диапазоне изменений.

В этой лекции мы покажем каким образом сократить количество вычислений, используя преобразования передаточных функций в сложной системе.

Большинство реальных систем автоматического регулирования являются сложными. При анализе часто приходится рассматривать как “фрагменты”, так полные системы САР, и выполнять над ними некоторые операции, упрощающие их структуру.

Определение. Действия, упрощающие математическое или графическое изображение САР (структуры) или упрощающие последующий анализ динамических свойств САР, называются структурными преобразованиями.

Различают несколько типовых упрощающих действий:

замена цепи из последовательно соединенных звеньев эквивалентным звеном;
замена цепи из параллельно соединенных звеньев эквивалентным звеном;
замена цепи с местной обратной связью эквивалентным звеном;
замена цепи с местной обратной связью на единичною обратную связь;
перенос точек включения обратной связи “вперед”- “назад”;
перенос точек суммирования или ветвления “вперед”- “назад”.

4.1 Замена цепи из последовательно параллельно соединенных звеньев

Рисунок 4.1.1. Последовательное соединение звеньев.

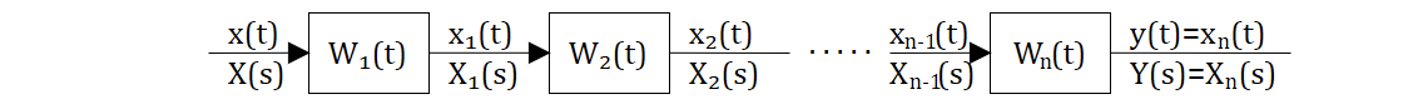
Цепь преобразований: Получить эквивалентную передаточную функцию:

$W_{экв}(s)=\frac{Y(s)}{X(s)}=\frac{X_n(s)}{X(s)};$

Запишем ряд очевидных равенств:

$\left \{ \begin{align}W_1(s) = \frac{X_1(s)}{X(s)}; \\ W_2(s)=\frac{X_2(s)}{X_1(s)}; \\ ................\\W_n(s)=\frac{X_n(s)}{X_{n-1}(s)};\end{align} \right.$

Перемножим, соответсвенно правые и левые части этих равентсв:

$W_1(s)\cdot W_2(s)\cdot \cdots \cdot W_n(s) = \frac{X_1(s)}{X(s)}\cdot \frac{X_2(s)}{X_1(s)}\cdot \cdots \cdot \frac{X_n(s)}{X_{n-1}(s)};$ $\frac{X_n(s)}{X(s)} =W_{экв}(s)=W_1(s)\cdot W_2(s)\cdots W_n(s);$

Эквивалентная передаточная функция:

$W_{экв}=\prod _{j=1}^{j=n}W_j(s); \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(4.1)}$

Найдем эквивалентную АФЧХ. (Подробнее см. лекцию Частотные характеристики систем автоматического управления (АФЧХ, ЛАХ, ФЧХ)).

$s = i \cdot \omega \Rightarrow W_{экв}(i\cdot\omega)=\prod_{j=1}^{j=n}W_j(i\cdot \omega) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(4.2)}$

Учитвая, что
$W_j = A_j(\omega)\cdot e^{i\cdot \phi_i(\omega)}\Rightarrow$

$\left \{ \begin{align} A_{экв}(\omega)=\prod_{j=1}^{j=n} A_j(\omega); \\ \phi_{экв}(\omega)=\sum_{j=1}^{j=n} \phi_j(\omega); \end{align} \right. \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(4.3)}$

Эквивалентная логарифмическая амплитудная характеристика ЛАХ:

$Lm_{экв}(\omega)=20 \cdot lg [A_{экв}(\omega)]=\sum_{j=1}^nLm_j(\omega) \ \ \ \ \ \ \ \ \ \ \ \mathbf{(4.4)}$

Если каждое из звеньев имеет передаточную функцию в виде $W_j(s) =K_j\cdot \frac{N(s)}{L(s)}$ , где у N(s) свободный член равен 1, а у L(s) свободный член = 0, то

$K_{экв}= \prod_{j=1}^n K_j \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(4.5)}$

Пример 1.

Заменить последовательные звенья структуры на рисунке 4.1.2 эквивалентным звеном и построить его логарифмическую амплитудную характеристику.

Рисунок 4.1.2 Последовательно соединенные звенья

Для начала вполним расчет эквивалентной передаточной функции по формуле 4.1:

$W_{экв}=\frac{\tau_1\cdot s}{T_1\cdot s+1}\cdot \frac{k_2}{T_2\cdot s+1}\cdot \frac{k3}{T_3\cdot s+1}\Rightarrow$ $W_{экв}=\frac{(\tau_1\cdot k_2\cdot k_3) s}{(T_1\cdot T_2\cdot T_3)s^3+(T_1\cdot T_2+T_1\cdot T_3+T_2\cdot T_3)\ s^2+(T_1+T_2+T_3) s+1}$

Если подставить вместо символьных коэффициентов их значение (см. рисунок 4.1.3) эквивалентаня передаточная функция примет вид:

$W_{экв}=\frac{100\cdot s}{s^3+101.01\cdot s^2+101.01\cdot s+1}$

Выполним аналогичное преобразование с помощью блока "Построение передаточных функций". На рисунке 4.1.3 представлена схема модели в которой выполняется расчет эквивалентной передаточной функции для трех последовательных звеньев.

Рисунок 4.1.3 Схема расчета эквивалентоно передаточной функции

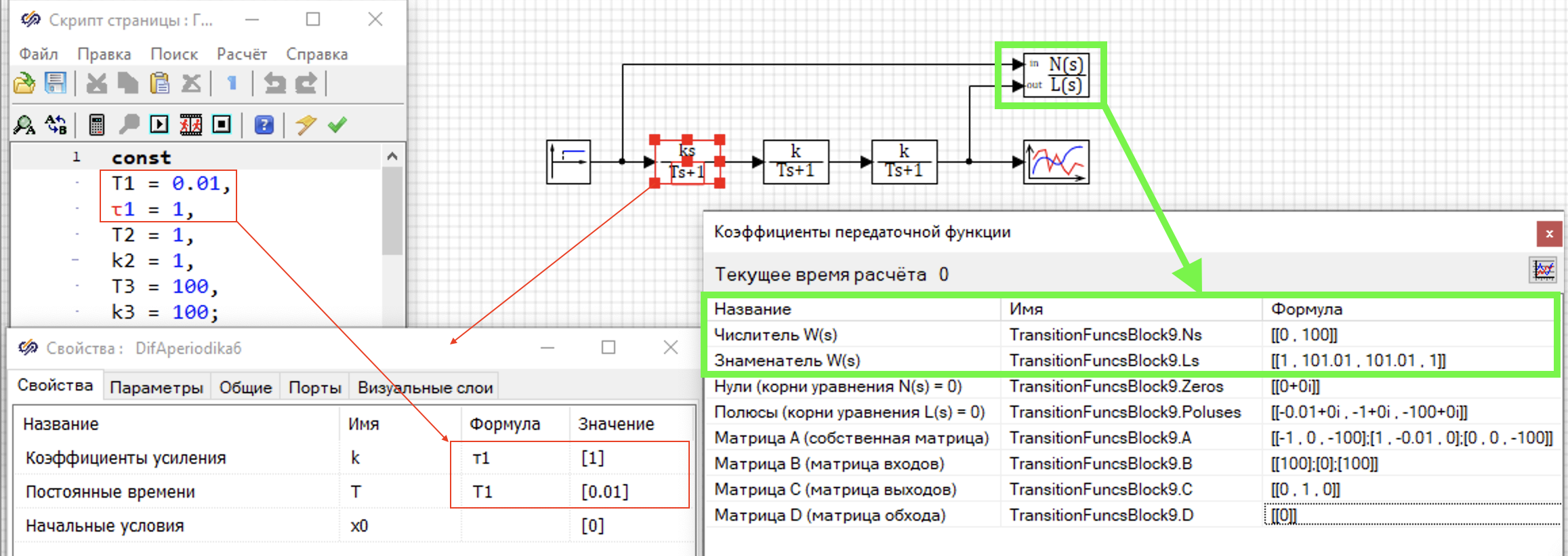
Численные значения коффициентов задаются в скрипте программы в секции констант, а затем используются в столбце формула, для свойств блоков - звеньев на схеме (красные прямоугольники на рис. 4.1.3). Блок "Построение передаточных функций" выполняет расчет коэффициентов, и результаты рассчета совппадают с аналитическим решением (зеленые прямоугольники на рис. 4.1.3).

Можно так же построить ЛАХ данной системы из трех звеньев, если сообразить, что на схема 4.1.2 испольуются блоки "Апереодическое звено первого порядка" и "Инерционно-дифференцирующее звено", которые мы рассматривали в соотвествующих лекциях ранее. Для каждого блока мы можем построить ЛАХ, используя формулы для точек перегиба функций, как это было показано ранее, а затем графически сложить для получения эквивалентной согласно формуле 4.4. Решение представлено на рисунке 4.1.4

Рисунок4.1.4 Построение эквивалентной ЛАХ

Проверим графическое аналитическое решение построекнием ЛАХ с помощью блока "Построение частотных характеристие". На рисунке 4.1.5 Представлена расчетная схема из трех последовательных звеньев и еквивалентное звено. Для каждого блока построена ЛАХ, и мы видим что точки перегиба и углы наклона функции совпадают.

Рисунок 4.1.5 ЛАХ последовательных звеньев и эквивалентного звена

4.2. Замена цепи из параллельно соединенных звеньев эквивалентным звеном

Рисунок 4.2.1 Система паралельных звеньев

Выходное значение является сумммой выходов из всех звеньев (см. рис. 4.2.1):

$y(t)=\sum^n_{j=1}x(t) \Rightarrow$ $Y(s)=\sum_{j=1}^n X_j(s)$

Запишем ряд очевидных равенства для передаточных функций:

$\left \{ \begin{align}X_1(s) = W_1(s)\cdot X(s); \\ X_2(s)=W_2(s)\cdot X(s); \\ ................\\X_n(s)=W_n(s)X(s);\end{align} \right.$

Складывая, получаем:

$\underbrace{X_1(s)+X_2(s)+...+X_n(s)}_{Y(s)}=X(s)\cdot\underbrace{[W_1(s)+W_2(s)+...+W_n(s)]}_{W_{экв}(S)}\Rightarrow$ $W_{экв}(s)=\sum_{j=1}^n W_j(s)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(4.6)}$

Найдем эквивиалентную АФЧХ, подставляя вместо значение $i\cdot\omega$ :

$W_{экв}(i\cdot \omega)=\sum_{j=1}^nW_j(i\cdot\omega) = \sum_{j=1}^nU_j(\omega)+i\cdot \sum_{j=1}^nV_j(\omega);\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(4.7)}$ $\left \{ \begin{align} U_{экв}(\omega)=\sum_{j=1}^{j=n} U_j(\omega); \\ V_{экв}(\omega)=\sum_{j=1}^{j=n} V_j(\omega); \end{align} \right. \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(4.8)}$

Модуль АФЧХ эквивалентной передаточной функции:

$A_{экв}(\omega)=\sqrt{\left[\sum_{j=1}^nU_j(\omega)\right]^2+\left[\sum_{j=1}^nV_j(\omega)\right]^2} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(4.9)}$

Фазовый сдвиг для эквивалентной передаточной функции:

$\phi (\omega)=-\pi\cdot m+arct\frac{V_{экв}(\omega)}{U_{экв}(\omega)}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(4.10)}$

где занчения m, зависит от положения вектора АФЧХ на векторной плоскости:

m = 1, 3, 5, ..., если вектор находится в 2 и 3 квадрантах комплексной плоскости,

m= 0,2,4, ..., если вектор находится в 1 и 4 квадрантах комплексной плоскости.

Логарифмическая амплитудная характеристика:

$Lm_{экв}(\omega)=20\cdot lg[A_{экв}(\omega)]=20\cdot lg\sqrt{\left[\sum_{j=1}^nU_j(\omega)\right]^2+\left[\sum_{j=1}^nV_j(\omega)\right]^2} \ \ \ \ \ \ \ \ \mathbf{(4.11)}$

Наиболее простые соотношения имеют место для переходной и весовой эквивалентных функций:

$h_{экв}(t)=\sum_{j=1}^nh_j(t); \ \ \ \ \ \ \ \ \ \ w_{экв}(t)=\sum_{j=1}^n w_j(t); \ \ \ \ \ \ \ \ \ \ \mathbf{(4.12)}$

Последовательное и параллельное соединение звеньев в значительной степени похожи на аналогичные соединения в электротехнике, гидравлики, и т.д.

Пример 2

Заменить паралельные звенья структуры на рисунке 4.2.2 эквивалентным звеном .

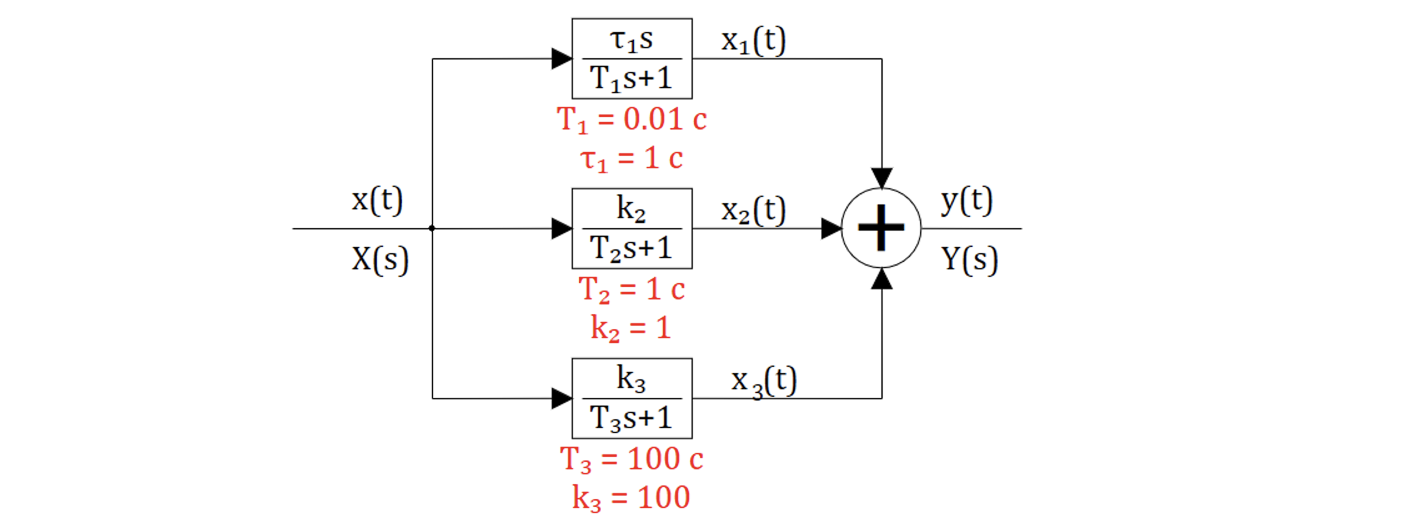
Согласно формуле 4.6 получим выражения для эквивалентной функции:

$W_{экв}=\frac{\tau_1\cdot s}{T_1\cdot s+1}+ \frac{k_2}{T_2\cdot s+1}+ \frac{k_3}{T_3\cdot s+1}\Rightarrow$ $W_{экв}=\frac{N_3\cdot s^3+N_2\cdot s^2+N_1\cdot s+N_0}{(T_1\cdot T_2\cdot T_3)s^3+(T_1\cdot T_2+T_1\cdot T_3+T_2\cdot T_3)\ s^2+(T_1+T_2+T_3) s+1}$

где значения многочлена числителя получаются путем приведения к общему знаменателю:

$N_3=\tau_1\cdot T_2\cdot T_3;\\ N_2=k_2\cdot T_1 \cdot T_3+k_3\cdot T_1 \cdot T_2+\tau_1\cdot T_3+\tau_1\cdot T_2;\\N_1 = \tau_1+k_2\cdot T_3+k_3\cdot T_2+k_3\cdot T_1; \\N_0=k_2+k_3.$

При подстановке численных значений коэффициентов с рисунка 4.2.2 получаем следующее значение эквивалентной передаточной функции:

$W_{экв}=\frac{100\cdot s^3+103\cdot s^2+202.01\cdot s+101}{s^3+101.01\cdot s^2+101.01\cdot s+1}$

Точно такое же значение получится при исползовании блока "Построение передаточных функций", для автоматически построения функций. Для сравнения построим переходный процесс для параллельных звеньев и эквивалентного звена:

Рисунок 4.2.3 Сравнение трех паралельных звеньев с эквивалетным звеном.

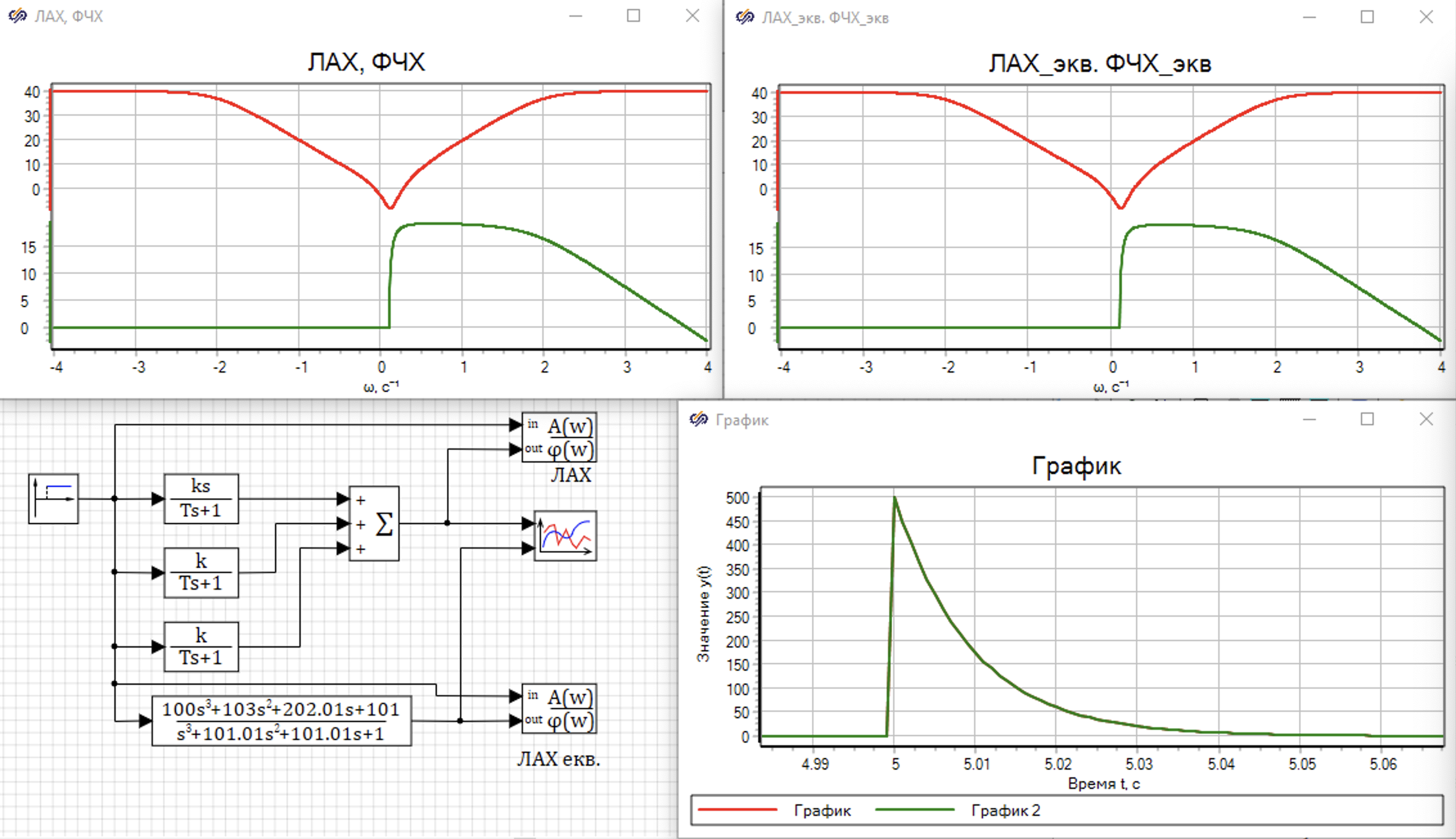
4.3 Цепь с обратной связью

Определение Связь выходного сигнала системы с входным, при которой отклонение выходного сигнала системы (т.е. объекта) вызывает соответствующее изменение ее входного сигнала, называется обратная связь.

Цепь с обратной связью имеет следующий структурный вид:

Рисунок 4.3.1 Струкутура системы с обратной связью

Определение: если обратная связь охватывает только часть цепи или одно звено, то такая связь называется местная обратная связь.

Если занчение сигнала обратной связи вычитается из входного сигнала, то такая связь называется отрицательной и может обозначатся на схема как "сравнивающее устройство" или просто знаком минус (см. рис. 4.3.2):

Рисунок 4.3.2 Обозначение отрицательной обратной связи

Если заначение сигнала обратной связи складывается с входным сигналом, то такая связь называется положительной, и обозначается знаком + (см. рис. 4.3.3).

Рисунок 4.3.3 Обзначение положительной обратной связи

Рассмотрим преобразование на примере отрицательной обратной связи см. рис. 4.3.4, которую нужно преобразовать в одно звено с эквивалентной передаточной функцией:

Рисунок 4.3.4 Преобрзование струкутруы с обратной связью.

На выходе из блока "Сравнивающее устройство" получается рассогласование:

$\varepsilon(t)=x(t)-x_{ос}(t) \Rightarrow E(s)=X(s)-X_{oc}(s)$

Выполним преобразования в изображениях обходя структуру по контору:

$Y(s)=E(s)\cdot W(s)=[X(s)-X_{oc}(s)]\cdot W(s) =\\ =[X(s)-Y(s)\cdot W_{oc}(s)]\cdot W(s) \Rightarrow \\ (1+W_{oc}(s)\cdot W(s))\cdot Y(s)=X(s)\cdot W(s);$

Эквивалентная передаточная функция для отрицательной обратной связи:

$W_{экв}(s)=\frac{Y(s)}{X(s)}=\frac{W(s)}{1+W_{ос}(s)\cdot W(s)} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(4.13)}$

Для положительной обратной связи преобразование аналогичные, за исключением знака обратной связи для величины "рассогласование" $\varepsilon(t) = x(t)+x_{oc}(t)$ тогда выражение эквивалентной функции для положительной обратаной связи по аналогии:

$W_{экв}(s)=\frac{Y(s)}{X(s)}=\frac{W(s)}{1-W_{ос}(s)\cdot W(s)} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(4.14)}$

Можно так же записать общее выражение для системы с обратной связью:

$W_{экв}(s)=\frac{W(s)}{1 \pm W_{ос}(s)\cdot W(s)} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(4.15)}$

где: знак " " - для отрицательной обратной свзязи, а знак " " - для положителеной

Как правило в регуляторах используется отрицательная обратная свзязь.

Опредление: обратная связь у которой значение сигнала выхода передается непосредственно на вход без передаточного зена, назвается единичная обратная связь.

В случае когда обратная связь единичная $W_{оc} = 1$ выражение для эквивалентной функции принимает вид:

$W_{экв}(s)=\frac{W(s)}{1 \pm W(s)} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(4.15)}$

Для единичной отрицательной обратной связи изображенной на рисунке 4.3.5 эквивалентная функция:

$W_{экв}=\frac{W(s)}{1+W(s)}$

Рисунок 4.3.5 Отрицательная единичная обратная связь.

Пример 3

Заменить звено с обратной связью структуры на рисунке 4.3.6 эквивалентным звеном.

Согласно формуле 4.13

$W_{экв}=\frac{\frac{\tau_1\cdot s}{T_1\cdot s+1}}{1+\frac{k_2}{T_2\cdot s+1}\cdot\frac{\tau_1\cdot s}{T_1\cdot s+1}}=\frac{\tau_1\cdot T_2\cdot s^2+\tau_1\cdot s}{T_1\cdot T_2\cdot s^2+(T_2+T_1+k_2\cdot\tau_1)\cdot s+1}$

Подставляя значения коэффициентов с рисунка 4.3.6 получаем следующие выражение передаточной функции:

$W_{экв}=\frac{s^2+s}{0.01\cdot s^2+2.01\cdot s+1}$

Рисунок 4.3.7 Сравнение системы с обратной связью и эквивалентной

4.3.1. Замена звена с местной обратной связью на единичную

Существуют два способа замены местной обратной связи на единичную:

Способ 1. Добавление последовательного звена после обратной связи, таким образом, что бы общая передаточная функция не изменилась (см. рис. 4.3.8):

Рисунок 4.3.8 Замена местной обратной связи.

Исходная передаточная функция согласно формулы 4.13:

$W_{ис}=\frac{W(s)}{1+W(s)\cdot W_{oc}(s)}$

Общая передаточная функция новой системы получается по формуле 4.1 для последовательных звенье, где первая часть это формула звена с единичной обратной связью, а вторая часть - новая неизвестная передаточная функция Z(s) см. рис. 4.3.8:

$W_{экв}=\frac{W(s)\cdot W_{oc}(s)}{1+W_{oc}(s)\cdot W(s)}\cdot Z(s);$

Приравнивая $W_{ис}=W_{экв}$ получаем выражение для добавленного звена:

$Z(s)=\frac{1}{W_{oc}(s)} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(4.18)}$

Cпособ 2. Добавление звена в контур до обратной связи так, что бы обратная единичная связь охватывала все звенья (см. рис. 4.3.9):

4.3.9 Замена обратной местной связи на единичную

Исходная передаточная функция согласно формулы 4.13:

$W_{ис}=\frac{W(s)}{1+W(s)\cdot W_{oc}(s)}$

Эквивалентаня функция для преобразованной схемы по формуле для последовательных звеньев 4.1 и для единичной обратной связи 4.15:

$W_{экв}=\frac{W(s)\cdot Z(s)}{1 +W(s)\cdot Z(s)}$

Приравнивая $W_{ис}=W_{экв}$ получаем выражение для добавленного звена:

$\frac{W(s)}{1+W(s)\cdot W_{oc}(s)}=\frac{W(s)\cdot Z(s)}{1+W(s)\cdot Z(s)} \Rightarrow$ $\Rightarrow 1+W(s)\cdot Z(s)=Z(s)+W(s)\cdot W_{oc}(s)\cdot Z(s) \Rightarrow$ $Z(s)=\frac{1}{1-W(s)+W(s)\cdot W_{oc}(s)}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(4.19)}$

4.3.2. Перенос места обратной связи “вперед” или “назад”

Перенос обратной связи вперед. Исходная и эквивалентная САР представлены на рисунке 4.3.10

Эквивалентная функция для исходной системы получим используя формулы для звена с обратной связью 4.13 и последовательного соединения 4.1:

$W_{исх}(s)=\frac{W_1(s)}{1+W_1(s)\cdot W_{oc}(s)}\cdot W_2(s)$

Эквиваланетная функция для преобразованной системы:

$W_{экв}=\frac{W_1(s)\cdot W_2(s)}{1+W_{ос}(s)\cdot Z(s)\cdot W_1(s)\cdot W_2}$

Приравнивая $W_{исх}=W_{экв}$ получаем:

$Z(s)=\frac{1}{W_2(s)} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(4.20)}$

Перенос обратной свзяи назад. Исходная и эквивалентная схемы представлены на рисунке 4.3.11

Рисунок 4.3.11 Перенос обратной связи назад

Аналогично запишем уравнения для обоих систем и определим значение добавленной передаточной функции:

$W_{исх}(s)=\frac{W_1(s)\cdot W_2}{1+W_1(s)\cdot W_{oc}(s)\cdot W_2(s)}=$ $=W_{экв}=\frac{W_1(s)\cdot W_2(s)}{1+W_{1}(s)\cdot W_{oc}(s)\cdot Z(s)}\Rightarrow$ $Z(s)= W_2(s)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(4.21)}$

4.4. Перенос точек суммирования “вперед” или “назад”

Такие преобразования достаточно просто илюстирируются графически.

На рисунке 4.4.1 перенос точки суммирования вперед:

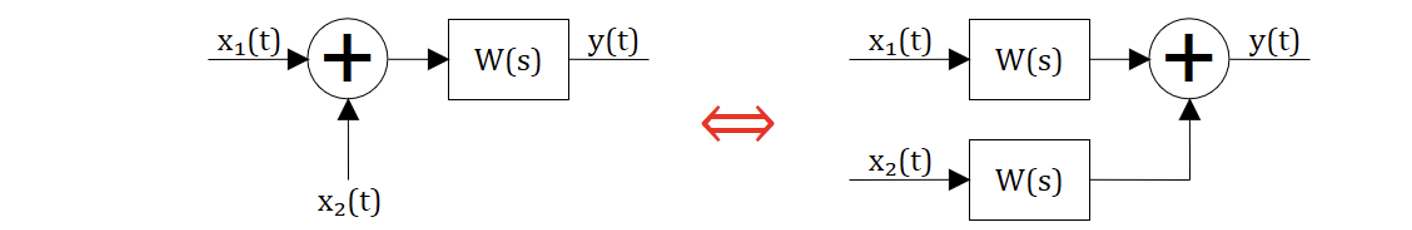
На рисунке 4.4.2 перенос точки суммирования назад:

Рисунок 4.4.2 Перенос точки сумирования назад

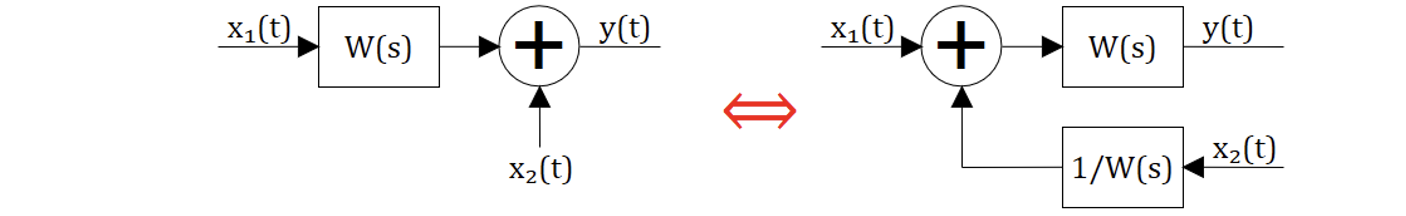
4.5. Перенос точек ветвления “вперед” или “назад”

На рисунках 4.5.1 и 4.5.2 представлены схемы переноса точек ветвления вперед и назад соответвенно:

Рисунок 4.5.1 Перенос точки ветвеления вперед

Рисунок 4.5.2 Перенос точки ветвления назад

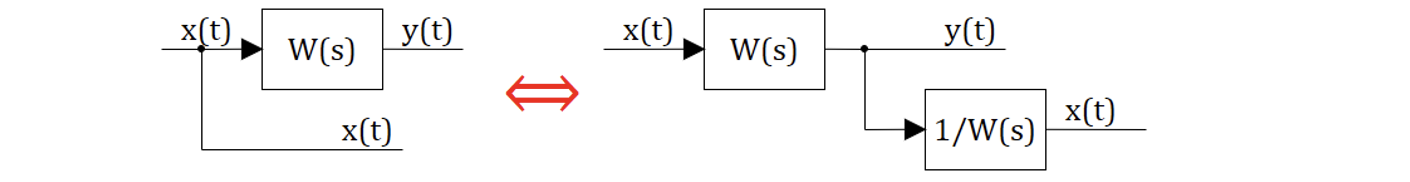
Данные рисунки очевидны и не требуют дополнительных комментариев. Иногда этот прием называется “перенос внешнего воздействия”.

Как всегда, примеры разобранные в лекции можно взять по ссылке здесь.

Предыдущие лекции:

1. Введение в теорию автоматического управления.
2. Математическое описание систем автоматического управления 2.1 — 2.3, 2.3 — 2.8, 2.9 — 2.13.
3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ РЕГУЛИРОВАНИЯ.
3.1. Амплитудно-фазовая частотная характеристика: годограф, АФЧХ, ЛАХ, ФЧХ. 3.2. Типовые звенья систем автоматического управления регулирования. Классификация типовых звеньев. Простейшие типовые звенья. 3.3. Апериодическое звено 1–го порядка инерционное звено. На примере входной камеры ядерного реактора. 3.4. Апериодическое звено 2-го порядка. 3.5. Колебательное звено. 3.6. Инерционно-дифференцирующее звено. 3.7. Форсирующее звено. 3.8. Инерционно-интегрирующее звено (интегрирующее звено с замедлением). 3.9. Изодромное звено (изодром). 3.10 Минимально-фазовые и не минимально-фазовые звенья. 3.11 Математическая модель кинетики нейтронов в «точечном» реакторе «нулевой» мощности.

Комментарии (2)

robomakerr
28.03.2022 18:17
#24210169
+1
легкий текст понятный даже школьнику!

Это вы погорячились)
1. petuhoff Автор
  29.03.2022 12:35
  #24212665
  Мы верим в наших школьников!