В первой части мы разобрались, зачем вообще могут быть нужны скруглённые дорожки и каплевидные подводы, а также реализовали необходимые для этого плагины. Эта же часть будет посвящена подстройке полученных плагинов под версию KiCad 6, в которой, к сожалению, пока полноценного функционала для скругления не появилось.

Вот мы и дождались KiCad 6, в котором появился новый функционал и кое-какие улучшения. Можно обратить внимание, что пользовательский интерфейс теперь поддерживает функцию Endless Pan (бесконечное панорамирование), также называемую Continuous Drag или Cursor Warping. Теперь, когда при панорамировании курсор мыши достигает края окна или монитора, это больше не становится преградой. Однажды попробовав эту возможность, жизнь без неё уже не представляешь.

Естественно, сама идея была позаимствована у Blender и привнесена в код KiCad не кем иным, как автором этих строк. В ходе этого процесса мы также исправили некоторые баги интерфейса в сборке для Windows. И хоть совершенным его не назовёшь, работает бесконечное панорамирование KiCad вполне неплохо.

Тем не менее больше всего пользователи ожидали от KiCad 6 нативной поддержки скруглённых дорожек. И они, наконец, появились. Но прежде чем мы попрощаемся с нашим плагином скругления, должен оговориться, что получили мы лишь ограниченную их поддержку, которая всё ещё находится на ранней стадии. Появившийся функционал вполне годится, чтобы скруглить пару углов, но далёк от того, чтобы сделать это для всей платы.

Нам обещали появление в KiCad 6 нового Python API, но это изменение было отложено до седьмой версии. Однако вполне ожидаемо, что сгенерированная SWIG обёртка не совпадает с её версией для KiCad 5. Изменились некоторые имена и методы, а значит, плагин скругления для работы в шестой версии нужно будет обновить. Ну а раз мы возьмёмся его обновлять, то можно попутно внести и кое-какие доработки.

▍ Fillet Tracks

Если в KiCad 6 выбрать две соединённые дорожки, вызвать контекстное меню, нажать Fillet Tracks и ввести значение радиуса, то сформируется дуга.


Затем заданный радиус можно изменять с помощью клика и перетаскивания созданного изгиба (без перетаскивания крайних точек).

В идеале должна быть возможность выбрать всё и нажать Fillet Tracks, чтобы применить скругление ко всей топологии. Но этот вариант не работает по ряду причин.

Во-первых, если радиус окажется слишком большим для выбранных дорожек, то программа выбросит предупреждение и дугу создавать откажется.


Во-вторых, если два угла находятся близко друг к другу, то скругление будет применено только к одному из них.


В-третьих, радиус не подстраивается на основе угла дорожки. Это становится наиболее заметно при наличии очень острых углов. На скриншоте ниже синим показаны исходные дорожки, зелёным — скругления, полученные в результате применения моего плагина, а красным – полученные через функцию Fillet Tracks. Во всех случаях радиус был установлен на 3мм.


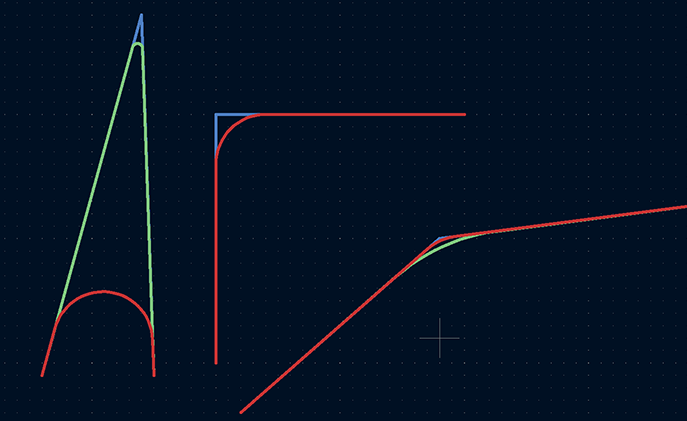
Когда угол равен 90⁰, оба метода скругления дают одинаковую форму, но для очень острого угла слева слепое использование радиуса в 3мм привело к съеданию большого объёма фигуры. В случае тупого угла справа изгиб с радиусом 3мм эффекта вообще почти не произвёл.

Четвёртая причина неудовлетворительности изгибов в том, что T-перекрёстки (или соединения от большего числа точек) полностью игнорируются.

Самым удачным вариантом здесь будет изменить плагин скругления для генерации изогнутых линий при помощи нативных дуг, решив тем самым перечисленные проблемы. В идеале применение этого плагина к топологии должно давать одинаковый визуальный результат при любом методе. Насколько это будет сложно сделать?

▍ Генерация дуг

Новый тип дорожек, PCB_ARC, можно инстанцировать несколькими способами. Метод, используемый внутренне при выборе Fillet Tracks, заключается в создании SHAPE_ARC, определении её радиуса и её касательного расположения относительно дорожек с каждого края. Затем из SHAPE_ARC инстанцируется PCB_ARC.

К сожалению, интерфейс Python не позволяет нам особых манипуляций с PCB_ARC. Можно считывать сгенерированные свойства, такие как радиус и угол, но при создании новой PCB_ARC единственными доступными для установки параметрами являются StartPoint, EndPoint и MidPoint.

Начальную и конечную точки найти несложно – достаточно укоротить дорожки, ведущие к пересечению. А вот для выяснения средней точки уже потребуется помощь тригонометрии.

Эта точка должна определять радиус, а также выравнивать дугу так, чтобы она располагалась касательно относительно ведущих к ней дорожек – в противном случае подстроить её впоследствии не получится, да и выглядеть она будет неправильно.

Решением, естественно, будет среднее взвешенное точек, основанное на факторе косинуса. Здесь я решил просто попробовать угадать — в итоге всё либо сработает идеально, либо получится в корне неверно. Часто бывает, что быстрее, оказывается, перебрать несколько догадок, прежде чем прибегать к рисованию чертежей.


К сожалению, несмотря на то, что новые дуги, очевидно, получились касательными (и с неверным радиусом, с чем мы разберёмся позже), интерактивная корректировка их скругления не помогала. Поначалу я решил, что это была ошибка скругления, но проблему удалось исправить, просто закрыв и повторно открыв файл.

Видимо, есть этап, анализирующий выравнивание дуг относительно дорожек, который не был автоматически активирован. Для исправления оказалось достаточно вызвать pcbnew.UpdateUserInterface(). Опробованное мной перед этим выполнение pcbnew.Refresh() привело к набору глюков, когда дуги отказывались двигаться. Надеюсь, эти детские болячки к следующим релизам подправят.

▍ Подбор радиуса

Похоже, что в ходе этих проектов «смягчались» не только схемы в KiCad, но и мои мозги. Чуть позже вы поймёте, о чём я.

Коэффициентом коррекции радиуса будет ещё одно тригонометрическое уравнение, и если с угадыванием предыдущего мне очень повезло, то на этот раз без рисования треугольников на бумаге, казалось, было не обойтись. О боже, избавь меня от этих треугольников на бумаге!

Вместо этого я решил поэкспериментировать — визуально выровнять множество дуг с их полученными подразделением двойниками при разных углах и записать координаты в электронной таблице. Это позволит построить график зависимости угла пересечения от поправочного коэффициента (соотношения ожидаемого и полученного радиусов). На основе этого будет уже намного проще подобрать уравнение, соответствующее точкам.


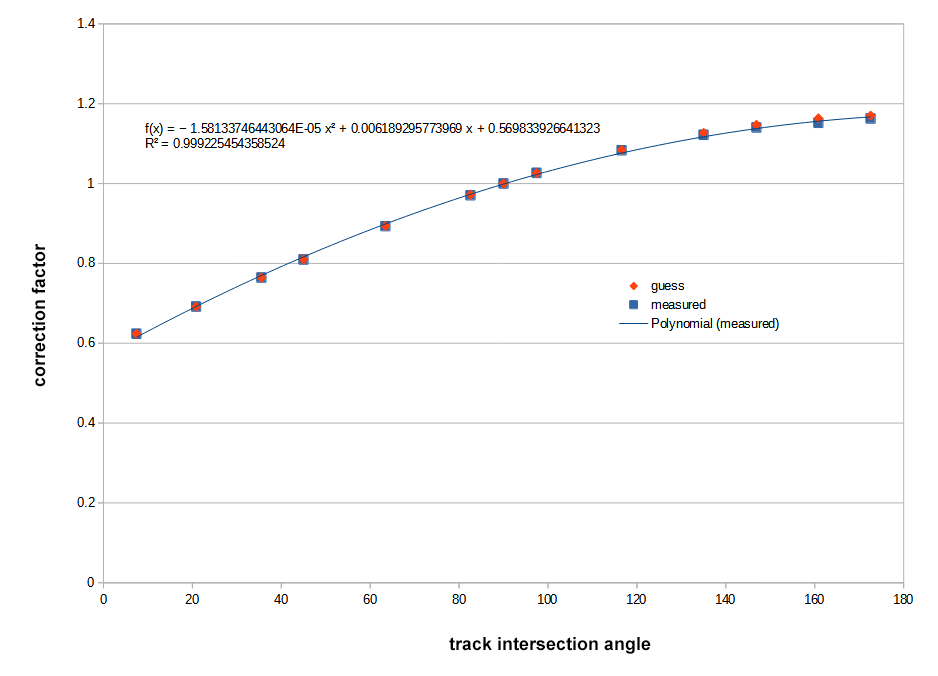
«Полезный» метод полиномиального приближения для кривой, очевидно, не даёт никакой подсказки, но искомый ответ был ( sin( angle/2 ) +1 ) * constant, где константа оказалась равна 0.585786…

Опишу процесс:

• очевидно, что эта фигура является частью синусоиды;
• это четверть сегмента, значит, она будет представлять функцию половинного угла;
• регулировка смещения и усиления примерно в районе 0.6 для того и другого;
• смещение и усиление одинаковы, значит, это константа, умноженная на sin(angle/2) + 1;
• при повороте 90⁰ коэффициент должен быть равен 1 по определению, значит, константа будет 1/(sin( 45 degrees )+1).

Вот чёрт! Константа 1/1.707… уже использовалась в другой части этого же фрагмента кода. Отсюда и доводы про размягчение мозга.


Ладно. Самое сложное позади, очередной задачей будут крутые повороты. При работе с квадратом (и радиусом больше его размера) процесс подразделения формирует круг. На первом этапе скругления отрезается около четверти участка вдоль линии. В результате от исходной дорожки остаётся лишь одна точка в центре.


В случае нативных дуг мы переходим сразу к результату: никогда не укорачивая дорожку больше, чем наполовину от её исходной длины. Если укорачивание происходит с двух сторон, удалите дорожку и привяжите обе дуги к центральной точке.


Красиво!

▍ T-образные и X-образные пересечения

T-пересечения относятся к допустимым случаям. А вот пересечения более высокого порядка – не совсем.


Эти пересечения уже почти работоспособны. В обоих случаях присутствует некая неравномерность из-за порядка, в котором обрабатываются дорожки. Если я когда-нибудь посчитаю, что пересечения от нескольких точек окажутся полезны на плате, то можно будет заняться доработкой.

▍ Каплевидные пады

Для полноценной работы этот плагин скругления необходимо подружить с плагином создания каплевидных подводов, над которым мы трудились в первой части.

К сожалению, апгрейд под нативные дуги их совместимость нарушил. Плагин для каплевидных подводов предполагает, что все дорожки у нас прямые, в результате чего нативные дуги ведут к созданию неправильных форм.


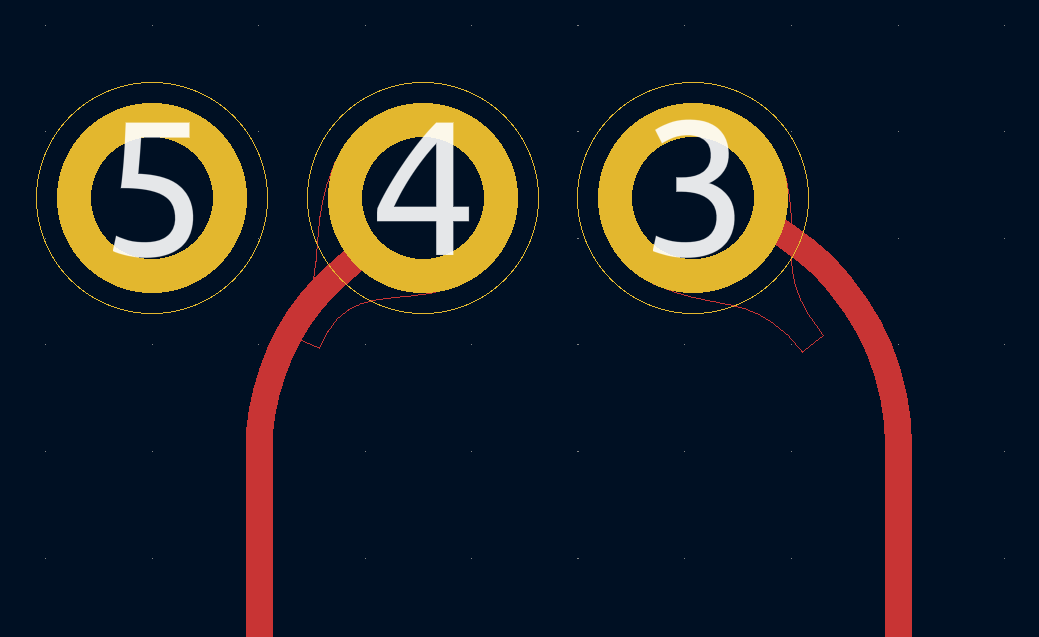
Но решить эту проблему будет несложно. Нужно лишь выяснить положение и вектор точки на определённом расстоянии вдоль дуги.

Интерфейс для добавления дуг весьма ограничен, но получить производные свойства дуг позволяет без проблем. У нас есть возможность взять углы (начальный, конечный и внутренний), а также радиус, центр дуги и именно фактическую длину, а не просто расстояние между крайними точками. Я мог бы утомить вас подробностями, но этого для решения проблемы уже достаточно.


В случае с прослеживаемыми дорожками всё немного хитрее, получается некий гибрид между прежним вариантом прослеживания для построения подразделяемых дуг и их новым форматом, но поскольку GetLength() возвращает правильную величину, большую часть кода можно оставить нетронутой.

На момент написания я отправил очередной запрос на слияние в репозиторий плагина для создания каплевидных подводов, но сам плагин ещё находится в процессе переноса в KiCad 6 (прим. пер.: возможно, к сегодняшнему дню этот процесс уже завершён).

▍ Заключение

Работа над плагином продолжается, но это уже всё довольно скучная рутина вроде исправления пограничных случаев и предотвращения аварийных завершений программы.

Одним из заметных бонусов в KiCad 6 стало добавление Plugin and Content Manager – репозитория плагинов, устанавливаемых одним кликом. Поскольку он никак не связан со скруглением, я не стану распинаться по поводу этого процесса, но, надеюсь, что в ближайшем будущем вы уже сможете установить плагин Round Tracks из этого менеджера.