
«How I Met Your Mother», season 6, ep. 7
Коля любит циклы.
Толя любит циклы.
Оля любит циклы.
Все любят циклы.
И Сережа тоже.Один Мамба их не любит. И вот почему.
Если опустить философские рассуждения, что все на уровне процессора является циклом или goto, то можно выделить три причины:
- При работе с индексами цикла можно легко проглядеть и допустить ошибку. Но тут помощь приходят итераторы.
- Очень часто циклы вручную пишутся очень неэффективно с точки зрения манипуляций с памятью — сильная просадка по производительности. А у вложенных циклов еще и накладные на старт цикла.
- Нелинейная структура цикла (
break,continue) не позволяют сделать хорошую оптимизацию на уровне процессора или компилятора. А это дополнительно означает, что распараллелить цикл по вычислителям будет очень трудно. В решении этого вопроса помогает функциональный подход и итераторы. Если известно о независимости вычислений значений каждого отдельного шага — надо сообщать об этом компилятору явно.
Просто поглядим на циклы на примере различных задачек.
От простого к более запутанному.

Пример 1. Итерирование по строкам
Есть замечательный map-цикл, который перебирает столбцы data.table-а
library(data.table)
library(magrittr)
data.table(
col_a = c(1, 2, 3),
col_b = c('id', 'aa', 'foo')
) %>%
purrr::map(~ print(.x))
# [1] 1 2 3
# [1] "id" "aa" "foo"Как нормально сделать так, чтобы он перебирал СТРОКИ (т.е. было 3 итерации, а не 2)?
Решение без циклов
Этому вопросу даже был посвящен целый доклад Jenny Bryan «Row-oriented workflows in R with the tidyverse». Тем не менее, поскольку с его появления прошло несколько лет, коснемся этого вопроса в текущем прочтении. Не забываем, что датафрейм не матрица, а тут он еще разнотипный. Ниже два различных подхода, функция paste взята условно, считаем, что она не является векторизованной.
library(tidyverse)
library(data.table)
# data.table::update.dev.pkg()
dt <- data.table(
col_a = c(1, 2, 3),
col_b = c('id', 'aa', 'foo')
)
bench::mark(
# Подход 1
# https://github.com/Rdatatable/data.table/issues/1732
# https://github.com/Rdatatable/data.table/blob/master/NEWS.md
# v1.14.3 п.39
dt[, s := paste(col_a, col_b, sep = "<>"), by = .I],
# Подход 2
rowwise(dt) %>%
mutate(s = paste(col_a, col_b, sep = "<>")),
check = FALSE
)## # A tibble: 2 × 6
## expression min median
## <bch:expr> <bch:tm> <bch:tm>
## 1 dt[, `:=`(s, paste(col_a, col_b, se ... 473.1µs 505.1µs
## 2 rowwise(dt) %>% mutate(s = paste(co ... 3.43ms 3.6msКак видим, разрыв в скорости более чем значительный. Выводы далее делайте сами.
Пример 2. Декартово произведение множеств
Есть два вектора. Надо проверить что-то для декартового произведения этих векторов. Какой путь будет best practice? Понимаю что векторизация выглядит лучше, но цикл более контролируемо (break и т.д.).
Навскидку видны пары путей.
# 1. Вложенный цикл
for (i in 1:10){
for(j in 2:3){
print(i*j)
}}
# 2. Итерирование через map/apply
expand.grid(1:10, 2:3) -> z
purrr::map2_dbl(z$Var1, z$Var2, .f = ~{.x * .y})Решение без циклов
Оставим авторскую формулировку, посмотрим на задачу декартового произведения множеств с точки зрения предлагаемых путей решения. Очевидно, что второй вариант лучше, но во второй строчке именно в этой задаче надо просто векторизацией обойтись.
Но можно отступить на шаг, отложить клавиатуру и взглянуть чуть по-другому. Что видим? Ба, да это же перемножение матриц, линейная алгебра, 1-ый курс.
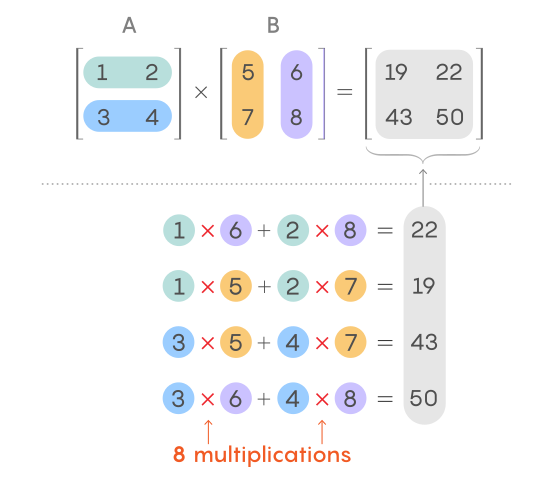
Получаем решение в одну строчку
matrix(1:10, ncol = 1) %*% matrix(2:3, nrow = 1)Но этого мало, даже в слегка оптимизированном и векторизованном виде прямые манипуляции разгромно проигрывают по скорости. 2-3 порядка!!!
m1 <- matrix(1:10, ncol = 1)
m2 <- matrix(2:3, nrow = 1)
z <- expand.grid(1:10, 2:3)
bench::mark(
m1 %*% m2,
transform(z, val = Var1 * Var2),
check = FALSE
)Пример 3. Оконные единичные матрицы
Вот такая условная постановка задачи. В реальности, размерность много больше 9.
Нужно найти 2 суммы по строке по разным диапазонам столбцов. С 1 по 3 строку
первое значение — диапазон суммирования 1:3 столбец, второе остальные столбцы,
с 4 по 6 строку первое значение — диапазон суммирования 4:6 столбец, второе
остальные столбцы, и последнее с 7 по 9 строку первое значение — диапазон
суммирования с 7:9 столбец, второе значение — остальные столбцы.
my_mat <- matrix(seq(1, 81), nrow = 9, ncol = 9, byrow = TRUE)
c1 <- rep(c(1, 4, 7), each = 3)
c2 <- rep(c(3, 6, 9), each = 3)
lapply(1:nrow(my_mat), function(i) {
cont <- my_mat[i, ]
c(sum(cont[c1[i]:c2[i]]),
sum(cont[-(c1[i]:c2[i])]))
})Решение без циклов
Пристально взглянув на задачу, видим, что решение достаточно простое. Бегущее окно 3*3 (спрайт) по диагонали. Разбиение суммы строки на часть в квадрате и остаток. Собственно, так дословно и будем решать. Опять помогает линейная алгебра и матрицы.
my_mat <- matrix(seq(1, 81), nrow = 9, ncol = 9, byrow = TRUE)
# создадим матрицу-окно
b1 <- unlist(rep(list(rep(1L, 3), rep(0L, 6)), 3))
b2 <- unlist(rep(list(b1, rep(0L, 3)), 3))
e_mat <- matrix(b2, ncol = 9, byrow = TRUE)[1:9, ]
# считаем задачу
s1 <- rowSums(my_mat * e_mat)
s2 <- rowSums(my_mat) - s1Выводим решение
tibble::tibble(s1, s2)## # A tibble: 9 × 2
## s1 s2
## <dbl> <dbl>
## 1 6 39
## 2 33 93
## 3 60 147
## 4 96 192
## 5 123 246
## 6 150 300
## 7 186 345
## 8 213 399
## 9 240 453Cамо скользящее окно
## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]
## [1,] 1 1 1 0 0 0 0 0 0
## [2,] 1 1 1 0 0 0 0 0 0
## [3,] 1 1 1 0 0 0 0 0 0
## [4,] 0 0 0 1 1 1 0 0 0
## [5,] 0 0 0 1 1 1 0 0 0
## [6,] 0 0 0 1 1 1 0 0 0
## [7,] 0 0 0 0 0 0 1 1 1
## [8,] 0 0 0 0 0 0 1 1 1
## [9,] 0 0 0 0 0 0 1 1 1Пример 4. Тайная связь между событиями
Есть data.frame исторических событий, и поиском расстояний найти одинаковые числа только не целыми значениями, а например: 1914-тигр, 1938-тигр расстояние = 24 года, сентябрь 1938-сентябрь 1940 = 24 месяца. Т.е. поиск одинаковых чисел как между 24 годами и 24000 часов — это будут одинаковые числа. 1986 Чернобыль Тигр — 2022 тигр = 36 лет, 26 апреля 1986 — 05 мая 2022.

Когда программист видит эту задачу, то тут же появляются циклы в циклах, матрицы расстояний и прочая гидра.
Задача раздувается и начинает требовать серьезных вычислительных ресурсов! Все как у взрослых.
Решение без циклов
Попробуем вспомнить алгебру. «Кольцо вычетов по модулю n» (пусть суровые математики сильно не возмущаются, могут быть терминологические неточности). Т.е. в постановке задачи всего-навсего требуется отклассифицировать все множество чисел классы вычетов по модулю n, где n будет соответствовать всяческим расстояниям, которые мы считаем значимыми. Задача решается в одну строчку!
Исключительно для демонстрации возьмем расстояние в одну неделю.
library(tidyverse)
# подготовим тестовые данные
t_df <- as.integer(runif(20, 19150, 19200)) %>%
unique() %>%
tibble(date = as.Date(., origin = "1970-01-01"), i_date = .)
# решаем задачу, например, ВСЕ ГРУППЫ дат в 7-дневном цикле
df <- mutate(t_df, grp = i_date %% 7)
vtree::vtree(df, "grp date", horiz = FALSE)
Вот и вся история. Едем дальше.
Пример 5. Цифровой храповик
Типичная задачка с собеседования. Вроде как ерунда, но есть нюансы.
Строим последовательность натуральных чисел для x от 1 до 10.
Есть индексы (1, 4, 7) с которых должен происходить инкремент последовательности на единицу.
Хочется получить z = 1, 1, 1, 2, 2, 2, 3, 3, 3, 3.
Программист тут же расчехляет циклы. Неинтересно, приземляем на взлете.
Решение без циклов
В целом, задача то важная. Это же практически вопрос про дискретизацию непрерывных функций.

Сделаем два решения. Первое — программистское решение именно поставленной задачи.
x <- rep_len(0L, 10)
y <- c(1,4,7)
x[y] <- 1L
cumsum(x)Но этого мало. Можно задачу обобщить, если немного подумать. По сути, нам надо построить функцию, являющуюся суммой трех функций Хевисайда. Ну и посчитать ее значение в 10-ти точках.
ff <- function(x) {
sum(purrr::map_dbl(c(1, 4, 7), ~ x >= .x))
}
purrr::map_dbl(1:10, ff) Пример 6. Серийные покупки
Есть айдишники клиентов, которые совершают покупки. Одни и те же клиенты могут совершать покупки несколько раз, поэтому их айдишники повторяются. Надо посчитать, какая это по счёту покупка конкретного клиента.
В питоне тут же начинают писать циклы в циклах. Цикл по покупателям, цикл по покупкам… Все потому, что циклы вбивают в голову на первых занятиях и далее только закрепляют это знание.
Решение без циклов
В нормальных аналитических языках это решается элементарно и без всяких закулисных манипуляций с индексами. Однократная сортировка позволяет прейти от хаоса к упорядоченным структурам. После этого подобный класс задач решается в одну строку.
library(data.table)
nn <- 20
dt <- data.table(id = sample(1:5, nn, replace = TRUE),
cost = runif(nn, 100, 200))
# решаем
dt[, tmp := 1L, by = id][, n_in := cumsum(tmp), by = id]Если посидеть и подумать, что становится очевидным, что и это избыточно и больше для демонстрации механики на счетах. Потому что достаточно в каждой группе (после физической сортировки, ведь там еще даты покупок могут быть) прогнать заполнение порядкового номера от 1 до длины группы с шагом 1.
dt[, n_in_grp := 1:.N, by = id]Это будет самый компактный и самый быстрый ответ на исходный вопрос.
id cost tmp n_in n_in_grp
<int> <num> <int> <int> <int>
1: 5 126.4575 1 1 1
2: 5 196.6588 1 2 2
3: 1 108.1415 1 1 1
4: 4 183.2515 1 1 1
5: 4 112.6702 1 2 2
6: 4 173.0156 1 3 3
7: 4 182.0650 1 4 4
8: 5 119.7534 1 3 3
9: 2 190.9689 1 1 1Пример 7. Пассажирские перевозки
Есть ежемесячная статистика по количеству перевезенных пассажиров. В переменной good_month Необходимо получить число пассажиров только в тех месяцах, в которых это число больше, чем показатель в предыдущем месяце.
Типовые шаги решения.
Всё, что в голову пришло пока — решение с циклом for, в котором if else осуществляет попарное сравнение элементов. Получается довольно громоздкая конструкция.
По идее нужно попарное сравнение a[1] с a[2], потом a[2] с a[3]… С этим я ещё работаю, но самые большие сложности возникают, когда надо заносить число пассажиров из месяца, который подошёл под условие, в новую переменную, т.к. оператор присвоения тут не подходит. В общем, путаница полная.
Решение без циклов
Пишем код исключительно тем способом, как и описано словами в задаче.
Без лишних наперсточных манипуляций.
Предварительную подготовку данных осуществляем ровно так же.
Подготовить список месяцев — значит именно так и делаем в коде.
В таком подходе из кода смысл считывается на раз. Даже без комментариев.
library(data.table)
library(magrittr)
# Seed:
set.seed(1)
# Сгенерируем набор тестовых данных
dt <- seq(as.Date("2005-01-01"), as.Date("2012-12-01"),
by = "1 month") %>%
format("%Y%m") %>%
data.table(ym = .) %>%
.[, `:=`(nr_pass = sample(1:100, .N), good_month = FALSE)]
# Решение
setorder(dt, ym) %>%
.[nr_pass > shift(nr_pass), good_month := TRUE]
dtВсе решение укладывается в одну строчку.
Пример 8. Выборка по пациентам
Возникло серьезное бутылочное горлышко в симуляции (нужно случайно отобрать по Pat_ID, а потом случайно отобрать внутри групп по Pat_ID одну строку). Никто не знает как сделать эффективно? Исходно в наборе данных несколько сотен тысяч строк.
Чтобы не тратить время, даже не будем затрагивать многослойный гамбургер с циклами, который будет предлагать каждый второй аналитик. Перейдем к существу вопроса.
Решение без циклов
Предположим, что записей чуть больше, чем заявляется. Чтобы чуть поинтереснее было.
Вариантов решения масса, но воспользуемся простой бинарной упаковкой с учетом объемных допущений.
Идея следующая. Свернем идентификаторы пациента и измерения в int32 хэш идентификатор.
Сначала сделаем оценочки
# Полагаем, что пациентов не более 10000
log(10^4) / log(2) # 14 бит
# А на каждого пациента не более 1000 записей
log(10^3) / log(2) # 10 бит
binaryLogic::as.binary(2^10)
# строим идентификатор на базе Int 32:
# пациент 31-11 биты, запись 10-1 битыlibrary(tidyverse)
library(data.table)
library(bench)
# готовим пример данных
df <- 1:10^4 %>%
tibble(pat_id = ., len = runif(length(.), 600, 900)) %>%
rowwise() %>%
mutate(val = list(sample.int(len, replace = FALSE))) %>%
ungroup() %>%
select(-len) %>%
unnest(val)
# решаем задачу
base_dt <- as.data.table(df) %>%
# строим хэш-идентификатор
.[, uid := .GRP * as.integer(2^10) + seq_len(.N), by = pat_id]
# сделаем выборку случайных N идентификаторов из каждой группы
# полное перемешивание
system.time({
dt <- data.table(shuff_uid = dqrng::dqsample(base_dt$uid, replace = FALSE)) %>%
# расщепляем обратно на пациента и группу
.[, pat_id := shuff_uid %/% 2^10] %>%
# оставим по 5 случайно перемешанных записей
.[, .(uid = head(shuff_uid, 5)), by = pat_id] %>%
# вливаем обратно данные по пациентам
.[, pat_id := NULL] %>%
merge(base_dt, all.x = TRUE, by = "uid")
})
skimr::skim(dt)Заодно еще раз посмотрим на разницу в производительности сэмплирования базовых и дополнительных библиотек. 5 раз — весьма ощутимый показатель, чтобы не обращать на него внимание.
# полное перемешивание
bench::mark(
base_dt[, shuff_uid := base::sample(uid, replace = FALSE)],
base_dt[, shuff_uid := dqrng::dqsample(uid, replace = FALSE)]
)## # A tibble: 2 × 6 ...
## expression ... min median
## <bch:expr> ... <bch> <bch:>
## 1 base_dt[, `:=`(shuff_uid, base::sample( ... 989ms 989ms
## 2 base_dt[, `:=`(shuff_uid, dqrng::dqsamp ... 228ms 229msДалее серия связанных задач по нарастающей.
Для тех, кто не знал, напомню, что и для data.table есть аналоги пакета tidyr.
В частности, tidyfast и tidyfst. Далее по ходу решения задач воспользуемся функциями по работе с list-column.
library(data.table)
data <- data.table(
x = c(1,2,3), y = c(2,3,4), z = list(c(1,2), c(1,1), c(2,3))
)
# Hate this:
tidyr::unnest(data,cols = c("z"))
# Ugly:
data[, lapply(.SD,unlist), by = 1:nrow(data)]
# Alternative:
tidyfst::unnest_dt(data, z)Пример 9. Считаем возрастные группы
Есть некоторое количество компаний. В них работают сотрудники разных возрастов, причем отдельные работают по совместительству. Требуется посчитать для каждой компании для каждого сотрудника количество коллег младше его.
Из сокращений ниже pid — personal_id, yob — year_of_birth, fid — firm_id.
Первоисточник задачи можно найти на SO.
library(data.table)
library(tictoc)
#Make it replicable:
set.seed(1)
#Define parameters of the simulation:
pid <- 1:1000
fid <- 1:5
time_periods <- 1:12
yob <- sample(seq(1900, 2010), length(pid), replace = TRUE)
#Obtain in how many firms a given pid works in a givem month:
nr_firms_pid_time <- sample(1:length(fid), length(pid), replace = TRUE)
#Aux functions:
function_rep<-function(x){
rep(1:12, x)
}
function_seq<-function(x){
1:x
}
#Create panel
data_panel <- data.table(pid = rep(pid,nr_firms_pid_time*length(time_periods)))
data_panel[, yearmonth := do.call(c,sapply(nr_firms_pid_time,function_rep))]
data_panel[, fid := rep(do.call(c, sapply(nr_firms_pid_time,function_seq)), each = 12)]
#Merge in yob:
data_yob <- data.table(pid = pid, yob = yob)
data_panel <- merge(data_panel, data_yob, by = c("pid"), all.x = TRUE)
#Solution 1 (terribly slow):
# make a small function that counts the number of coworkers with
# earlier dob than this individual
older_coworkers = function(id, yrmonth) {
#First obtain firms in which a worker works in a given month:
id_firms <- data_panel[pid == id & yearmonth == yrmonth, fid]
#Then extract data at a given month:
data_func <- data_panel[(fid %in% id_firms) & (yearmonth == yrmonth)]
#Then extract his dob:
dob_to_use <- unique(data_func[pid == id,yob])
sum(data_func[pid!=id]$yob < dob_to_use)
}
#Works but is terrible slow:
tic()
sol_1 <- data_panel[, .(older_coworkers(.BY$pid, .BY$yearmonth)), by = c("pid", "yearmonth")]
toc()
#Solution 2 (better but do not like it, what if I want unique older coworkers)
function_older <- function(x){
noc <- lapply(
1:length(x),
function(i){
sum(x[-i] < x[i])
}
)
unlist(noc)
}
fSol2 <- function(dt){
dt[, .(pid, function_older(yob)),by = c("fid", "yearmonth")][, sum(V2),by = c("pid", "yearmonth")][order(pid, yearmonth)]
}
# This is fast but I cannot get unique number:
tic()
sol_2 <- fSol2(data_panel)
toc()
# Everything works:
identical(sol_1, sol_2)Имеем времена решения ~70 секунд в первом случае и ~0.7 секунд во втором. Вроде как циклов явных нет и время вроде ничего, только lapply немного беспокоит.
Решение без циклов
Попробуем собрать альтернативное решение без lapply Будем достигать двух целей — повышения читаемости кода и повышение производительности.
Для начала можно попробовать применить non-equi join с последующей агрегацией. Этот вариант заведомо плох тем, что пойдет "раздувание" данных, но просто поглядим.
# подтягиваем все uid, которые по возрасту меньше
df <- data_panel %>%
.[data_panel[, .(pid, yearmonth, fid, yob_x = yob)],
.(x.pid, i.pid, yearmonth, fid),
on = .(yearmonth, fid, yob < yob_x)] %>%
.[, .N, by = .(x.pid, yearmonth)]
dfПолучаем на обычном ноуте ~2 секунды на тестовом сэмпле. Не фонтан, но выглядит более понятно и компактно.
А теперь давайте подумаем над сутью происходящего. Старшинство людей по возрасту не зависит от положения в пространстве, но зависит только от взаимного расположения по шкале времени. однократная физическая сортировка всех людей по шкале времени приведет нас от хаоса к упорядоченному множеству. И мы для каждого человека можем легко и просто понять число более молодых сотрудников, просто глянув на его индекс в этом отсортированном списке!
Казалось бы, что ситуация несколько усложняется за счет того, что год рождения может совпадать у многих людей — как их сортировать по возрасту? Но это неважно, мы же считаем только тех, кто моложе, а для этого достаточно всех погодков свернуть в список (вот и list-column) и использовать этот количественный модификатор для подсчета очереди.
Получаем линейную функцию всего в несколько строчек.
library(data.table)
fSol3 <- function(dt){
dt %>%
.[, .(pid = list(pid)), by = .(yearmonth, fid, yob)] %>%
.[, ll := lengths(pid)] %>%
setorder(yob) %>%
.[, n_corr := shift(cumsum(ll), fill = 0, type = "lag"),
by = .(fid, yearmonth)] %>%
tidyfst::unnest_dt(pid) %>%
# суммируем по персонажам
.[, .(V1 = sum(n_corr)), by = .(pid, yearmonth)]
}Заодно упростим функцию генерации тестового датасета. В итоге, путем простых умозаключений имеем ускорение еще примерно на порядок!
library(tidyverse)
set.seed(1)
# генерим датасет, сначала справочник пользователей, потом обвес
udict_df <- tibble(pid = 1:1000) %>%
# год рождения и число фирм в которых работал
mutate(yob = sample(1900:2010, nrow(.), replace = TRUE),
nf = sample(1:5, nrow(.), replace = TRUE))
data_df <- udict_df %>%
rowwise() %>%
# вгоняем идентификаторы фирм и месяца
mutate(fid = list(sample(1:5, nf)), yearmonth = list(1:12)) %>%
ungroup() %>%
select(-nf) %>%
unnest(cols = fid) %>%
unnest(cols = yearmonth)
# dt <- as.data.table(data_df)
dt <- copy(data_panel)
tic()
res_dt <- fSol3(dt)
toc()
dplyr::all_equal(sol_2, res_dt)
waldo::compare(sol_2, setorder(res_dt, pid, yearmonth))
bench::mark(
fSol2(data_panel),
fSol3(dt),
check = FALSE
)Ну «ничоситак» на ровном месте.
A tibble: 2 × 6
## expression min median `itr/sec` mem_alloc `gc/sec`
## <bch:expr> <bch:tm> <bch:tm> <dbl> <bch:byt> <dbl>
## 1 fSol2(data_panel) 318.2ms 319.7ms 3.13 515.39MB 3.13
## 2 fSol3(dt) 1.5s 1.5s 0.665 4.45MB 0Пример 10. Ускоряем Difference-in-Differences
Есть в эконометрике такой метод — расчет разностей показателей на входе и на выходе. «Difference in Differences» (DID).
Индексы целочисленные, можно в разреженную матрицу превратить, а можно и через data.table.
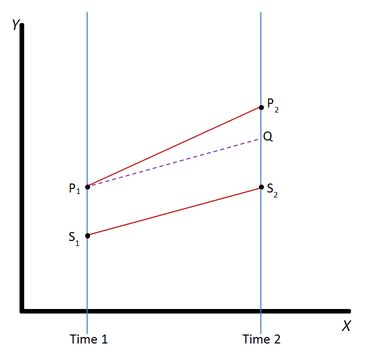
Ниже пример попытки самостоятельного расчета с классическим применением циклов.
В теории считает верно, на практике имеем засаду.
Когда количество груп и периодов большое (в примере тут есть четыре групы), есть задача где есть 1000 груп и 300 периодов, это работае очень медленно.
library(data.table)
library(tidyverse)
#Make it replicable:
set.seed(1)
#Define parameters:
n_units <- 1000
n_periods <- 100
#Generate the data:
#First define units and when they are treated:
data <- data.table(
fid = 1:n_units,
treat_time = sample(c(0L, 25L, 75L, 50L), n_units, replace = TRUE)
)
#Then add time:
data <- data[rep(data[, .I], n_periods)]
setorder(data, fid)
data[, time := rep(1:n_periods, n_units)]
#Add outcome:
data[, y := rnorm(n_units * n_periods)]
# plot(density(data$time))
#Now start's the fun:
#For each group defined by treat_time
#I want to calculate the sample version of the following object:
#(E[y|treat_time = x,t = t] - E[y|treat_time = x,t = treat_time-1]) - (E[y|treat_time = 0,t = t] - E[y|treat_time = 0,t = treat_time-1])
#For example for group 25:
(mean(data[treat_time == 25 & time == 2, y]) - mean(data[treat_time == 25 & time == 24, y])) -
(mean(data[treat_time == 0 & time == 2, y]) - mean(data[treat_time == 0 & time == 24, y]))
#For group 25 for all time periods the solution would be something like this:
for (t in 1:n_periods){
(mean(data[treat_time == 25 & time == t, y]) - mean(data[treat_time == 25 & time == 24, y])) -
(mean(data[treat_time == 0 & time == t, y]) - mean(data[treat_time == 0 & time == 24, y]))
}Есть различные пакеты на CRAN, например, did, did2s. При большом количестве точек и групп, со слов аналитиков их использующих, начинается нехватка скорости вычислений. Заглядывая под капот видим там наличие циклов.
Поскольку сама по себе методика не сильно сложная, можно попробовать сделать этот расчет самостоятельно и без использования циклов.
Посмотрим на формулу расчета. Она выглядит достаточно просто (a-b)-(c-d) = a+d-b-c. Беда в том, что при полном переборе придется многократно пересчитывать эти константые элементы.
Отсюда виден план действий:
- Вытаскиваем за скобки расчеты элементов матрицы.
- Формируем сетку расчетов.
- В один проход для каждого элемента сетки заполняем значения
a, b, c, dи считаем формулу.
# похоже на матрицы, попробуем провести различные атомарные свертки
# индексы целочисленные, можно в разреженную матрицу превратить
# а можно и через data.table
dt <- copy(data) %>%
.[, .(y_mean = mean(y)), by = .(treat_time, time)]
# конструируем сетку расчёта
# (E[y|treat_time = x,t = t] - E[y|treat_time = x,t = treat_time-1])
- (E[y|treat_time = 0,t = t] - E[y|treat_time = 0,t = treat_time-1])
df <- expand_grid(x = unique(dt$treat_time),
t = unique(dt$time)) %>%
# формируем кординаты для слияния
mutate(i1 = x, j1 = t, i2 = x, j2 = x - 1,
i3 = 0, j3 = t, i4 = 0, j4 = x - 1) %>%
# нанизываем слагаемые
left_join(dt[, .(i1 = treat_time, j1 = time, a = y_mean)]) %>%
left_join(dt[, .(i2 = treat_time, j2 = time, b = y_mean)]) %>%
left_join(dt[, .(i3 = treat_time, j3 = time, c = y_mean)]) %>%
left_join(dt[, .(i4 = treat_time, j4 = time, d = y_mean)]) %>%
mutate(var = (a - b) - (c - d))Ускорение на несколько порядков, код прозрачен и компактен.
Заключение
Заглядывайте в группу, задавайте вопросы. Иногда там даже ответы бывают.
Предыдущая публикация — «Data Science — это не только подсчет пельменей…».

