В июне 2015 года в России был принят стандарт блочного шифрования — ГОСТ Р 34.12-2015. Мне стало интересно объединить этот ГОСТ (точнее, полином, который используется в нем) и схему Блома.

Вооружившись исходниками и самим ГОСТом, я приступил к делу. Но для начала немного теории.

Итак, Схема Блома —схема предварительного распределения ключей в сети связи. Принцип её действия таков:



Есть симметричная квадратная матрица T:



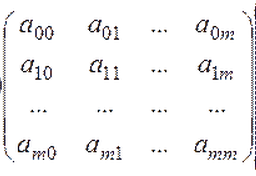
Матрица, как правило, содержит столько строк (и столбцов), сколько абонентов в сети. Так, при 20 абонентах, матрица имеет размер не меньше 20*20.

Открытые ключи абонентов А и В:





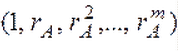
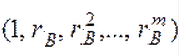
Открытые ключи, как правило, формируются по принципу матрицы Вандерморта, где первый элемент строки — число в нулевой степени, второе число — в первой, n-ое число — в n-ой степени. В нашей программе первым элементом каждой строки будет число в первой степени, а не в нулевой:

.

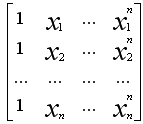Так формируются все открытые ключи для всех обонентов.

Если взять открытый ключ абонента А и умножить его на матрицу T, мы получим секретный ключ абонента А:



То же самое делается для всех абонентов сети. Этим занимается доверенная сторона, которая затем раздаёт каждому участнику открытый и закрытый ключ. Участники, обмениваясь между собой только открытыми ключами по незащищённым каналам связи, могут сгенерировать секретный сеансовый ключ для общения между собой.

Надёжность схемы напрямую зависит от размера секретной матрицы, используемой в схеме. Для восстановления секретной матрицы необходимо иметь число ключей, равное количеству строк матрицы. После этого секретный ключ абонента А умножается на открытый ключ абонента В — так получается сеансовый ключ.

Для наглядности небольшой пример на маленьких числах, взятый здесь:

Доверенный центр выбирает размер конечного поля и секретную матрицу:



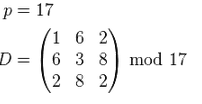
Абоненты выбирают себе идентификаторы (как правило выдаются доверенным центром):



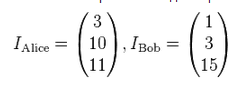
Доверенный центр вычисляет закрытые ключи:



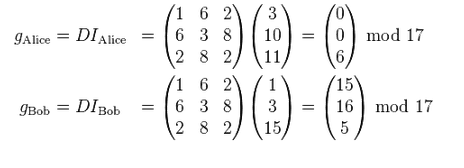
После этого каждая из сторон вычисляет секретный ключ, умножая свой закрытый ключ на идентификатор второй стороны:



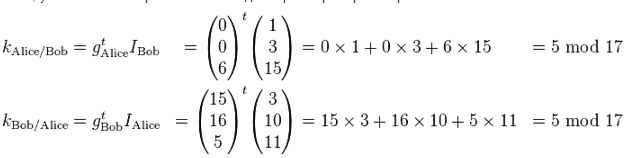
Как видно на примере, получается одинаковый ключ.

Тереть реализуем это в С++

Для начала создадим и заполним нашу матрицу. Для наглядности сделаем её 8*8:

	
randomize();
	for (int i = 0; i < 8; i++) {
		for (int j = 0; j < 8; j++) {
			if (j >= i) {
				mass[i][j] = random(255);
			}
		}
	}
	for (int i = 0; i < 8; i++) {
		for (int j = 0; j < 8; j++) {
			mass[j][i] = mass[i][j];
		}
	}

Также подключим к нашему проекту table.h, в которой, по сути, записаны все возможные умножения полинома, который используется в ГОСТе, на самого себя, только сдвинутого.

#include "table.h"

Инициализируем переменные, которые нам пригодятся:

	int zakr3[8] = {NULL}; // закрытые
	int zakr2[8] = {NULL}; // ключи

       	int abon3[8] = {NULL}; //открытые ключи 
	int abon2[8] = {NULL}; // абонентов

        int secret3[8] = {NULL};// секретные 
	int secret2[8] = {NULL}; // ключи

В Edit-ы вводим номера абонентов, которые затем считываем:

                abon2[0] = StrToInt(Edit1->Text);
		abon3[0] = StrToInt(Edit2->Text);

Далее, используя принцип матрицы Вандерморта, «добиваем» строки открытых ключей до полного заполнения:

for (int j = 1; j < 8; j++) {
			sum3 = multTable[abon3[j - 1] + 256 * StrToInt(Edit1->Text)];
			sum2 = multTable[abon2[j - 1] + 256 *StrToInt(Edit2->Text)];
			abon2[j] = sum2; // последующие
			abon3[j] = sum3; // элементы
		}

multTable- это тот самый table.h, который мы подключали ранее. Пришло время формировать закрытые ключи:

		for (int j = 0; j < 8; j++) {
			int x1= 0,x2 = 0; //вспомогательные переменные 
			for (int y = 0; y < 8; y++) {
				sum3 = multTable[mass[j][y] + 256 * abon3[y]];
				sum2 = multTable[mass[j][y] + 256 * abon2[y]];
				x1 = x1^ sum3;
				x2 =x2 ^ sum2;
			}
			// закрытые ключи:
			zakr3[j] = x1;
			zakr2[j] = x2;
		}

Здесь применяется правило умножения строки на матрицу, за тем исключением, что вместо обычного сложения используем сложение по модулю 2. В результате получим строку, состоящую из 8 элементов.

Далее нам предстоит вычислить общий секретный ключ.

		sum3 = NULL;
		sum2 = NULL;
		for (int y = 0; y < 8; y++) {
			secret3[y] = multTable[256 * zakr3[y] + abon2[y]]; // итог
			secret2[y] = multTable[256 * zakr2[y] + abon3[y]]; // итог
			sum3 = sum3 ^ secret3[y]; //секретный ключ абонента В
			sum2 = sum2 ^ secret2[y];//секретный ключ абонента А
		}

Здесь происходит умножение строки на столбец. В результате получается число. Если все сделать правильно, то sum2 и sum3 должны быть одинаковыми. Вот в принципе и все. В данном примере я использовал int-овские числа, но никто не запрещает использовать числа большей размерности.

Источники:

• habrahabr.ru/post/266359
• ru.wikipedia.org/wiki/Определитель_Вандермонда
• www.myshared.ru/slide/713101
• ru.wikipedia.org/wiki/Схема_Блома