Каждый аудиосигнал содержит характеристики. Из MFCC (Мел-кепстральных коэффициентов), Spectral Centroid (Спектрального центроида) и Spectral Rolloff (Спектрального спада) я провела анализ аудиоданных и извлекла характеристики в виде среднего значения, стандартного отклонения и skew (наклон) с помощью библиотеки librosa.

Для классификации “живого” голоса (класс 1) и его отделению от синтетического/конвертированного/перезаписанного голоса (класс 2) я использовала алгоритм машинного обучения - SVM (Support Vector Machines) / машины опорных векторов. SVM работает путем сопоставления данных с многомерным пространством функций, чтобы точки данных можно было классифицировать, даже если данные не могут быть линейно разделены иным образом. Для работы я использовала математическую функцию, используемой для преобразования (известна как функция ядра) - RBF (радиальную базисную функцию).

В первой части анализа аудиоданных разберем:

• Загрузку аудиофайла с помощью библиотеки librosa (посмотрим на размер и содержание аудиофайла, установим проигрыватель аудио в Jupyter Notebook и посмотрим, как выглядит звук );

• Разделение гармонических (тональных ) и ударных (переходных) сигналов;

• Извлечение битов - Beat;

• Нормализованную энергию цветности (функции цветности, Chroma Energy Normalized (CENS));

• Мел-кепстральные коэффициенты (MFCC);

• Спектрограммы;

• Спектральный центроид (Spectral Centroid);

• Спектральный контраст (Spectral Contrast);

• Спектральный спад ( Spectral Rolloff);

• Спектральная ширина ( Spectral bandwidth);

• Скорость пересечения нуля - Zero Crossing Rate

Для анализа аудиоданных необходимо установить библиотеку librosa. В терминале прописываем:

pip install librosa

Теперь можно импортировать необходимые библиотеки:

%matplotlib inline  
import librosa
import librosa.display
import IPython
import numpy as np
import pandas as pd
import scipy
import matplotlib.pyplot as plt
import seaborn as sns

Загрузка аудиофайла:

audio_data = '../input/audioset/Training_Data/human/human_00004.wav'
y, sr = librosa.load(audio_data)
print(type(y), type(sr))

<class 'numpy.ndarray'> <class 'int'>

Библиотека librosa загружает и декорирует звук, как временной ряд.

y - представлен как одномерный массив numpy.

sr - содержит частоту дискретизации y, то есть количество отсчетов звука в секунду.

По умолчанию весь звук микшируется в моно и происходит Передискретизация до 22050 Гц во время загрузки.

Частота дискретизации (Sample Rate) - это количество аудио сэмпла, передаваемых в секунду, которое измеряется в Гц или кГц (число выборок аудиосигнала, приходящихся на секунду).

Посмотрим на размер аудиофайла:

print(y.shape, sr)

(76734,) 22050

Посмотрим на переменные y, sr:

print(y, sr)

[-5.8037718e-04 -5.1912345e-04 -3.2173379e-04 ... -2.0331862e-04 -5.4037344e-05 2.2379844e-04] 22050

С помощью IPython.display можно проигрывать аудио в Jupyter Notebook, а с помощью display.waveplotформируются звуковые волны и мы можем посмотреть, как выглядит звук:

import IPython.display as ipd
plt.figure(figsize=(14, 5))
librosa.display.waveplot(y, sr=sr)
ipd.Audio(audio_data)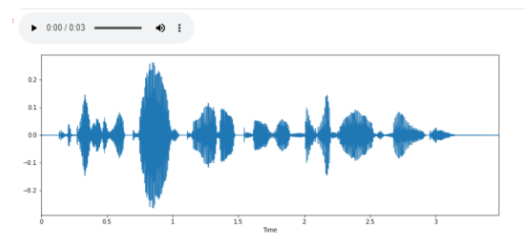

Разделение гармонических (тональных ) и ударных (переходных) сигналов на две формы волны:

# Seperation of Harmonic and Percussive Signals
y_harmonic, y_percussive = librosa.effects.hpss(y)
plt.figure(figsize=(15, 5))
librosa.display.waveplot(y_harmonic, sr=sr, alpha=0.25)
librosa.display.waveplot(y_percussive, sr=sr, color='r', alpha=0.5)
plt.title('Harmonic + Percussive')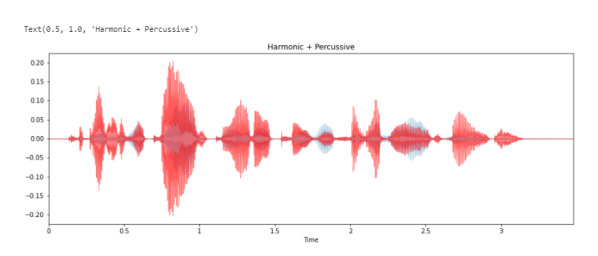

Результатом является то, что временной ряд y был разделен на два временных ряда, содержащих гармоничную и ударную части сигнала. Каждый из y_harmonic и y_percussive имеет ту же форму и продолжительность, что и y.

Извлечение битов - Beat.

Beat (бит) трек на ударном сигнале. От англ. beat – один удар бочки - отрезок времени, ритм. Так, в одном такте 4 бита, например. Такт логичное деление битов. Обычно в такте 3 или 4 бита, хотя возможны и другие варианты.

Из аудио можно получить темп и биты:

# Beat Extraction
tempo, beat_frames = librosa.beat.beat_track(y=y_percussive,sr=sr)
print('Detected Tempo: '+str(tempo)+ ' beats/min')
beat_times = librosa.frames_to_time(beat_frames, sr=sr)
beat_time_diff=np.ediff1d(beat_times)
beat_nums = np.arange(1, np.size(beat_times))

fig, ax = plt.subplots()
fig.set_size_inches(15, 5)
ax.set_ylabel("Time difference (s)")
ax.set_xlabel("Beats")
g=sns.barplot(beat_nums, beat_time_diff, palette="BuGn_d",ax=ax)
g=g.set(xticklabels=[])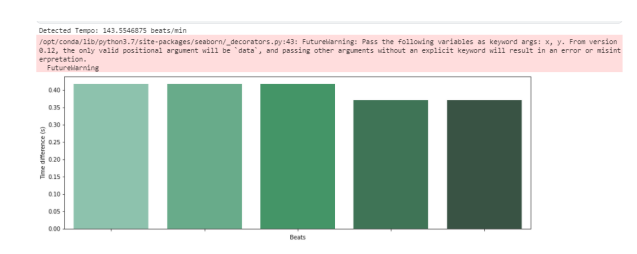

Нормализованная энергия цветности - Chroma Energy Normalized (CENS)

Функции цветности основаны на двенадцати атрибутах написания основного тона, как используется в западной нотной записи, где каждый вектор цветности указывает, как энергия в кадре сигнала распределяется по двенадцати полосам цветности. Измерение таких распределений во времени дает представление времени и цветности (или хромаграмму ), которое тесно коррелирует с мелодической и гармонической прогрессией. Такие последовательности часто схожи для разных записей одного и того же. Нормализованная энергия цветности применяется для сопоставления звука, где допускаются вариации, поскольку они обычно появляются в разных исполнениях . Например, два разных исполнения одного и того же, могут демонстрировать значительные нелинейные глобальные и локальные различия в темпе, артикуляции и фразировке.

#Chroma Energy Normalized (CENS)
chroma=librosa.feature.chroma_cens(y=y_harmonic, sr=sr)
plt.figure(figsize=(15, 5))
librosa.display.specshow(chroma,y_axis='chroma', x_axis='time')
plt.colorbar()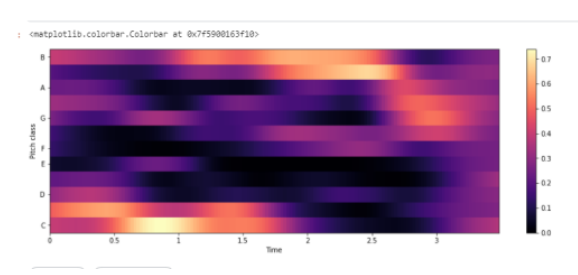

Мел-кепстральные коэффициенты (MFCC).

Мел-кепстральные коэффициенты — один из важнейших признаков в обработке аудио. MFCC — это матрица значений, которая захватывает тембральные аспекты.

MFCC - Представляют собой набор признаков , которые описывают общую форму спектральной огибающей. Они моделируют характеристики человеческого голоса. MFCC - коэффициенты частотной капсулы, суммируют частотное распределение по размеру окна. Поэтому можно анализировать как частотные, так и временные характеристики звука. Перед построением графика коэффициенты нормализуются.

# Calculate MFCCs
mfccs = librosa.feature.mfcc(y=y_harmonic, sr=sr, n_mfcc=20)
plt.figure(figsize=(15, 5))
librosa.display.specshow(mfccs, x_axis='time')
plt.colorbar()
plt.title('MFCC')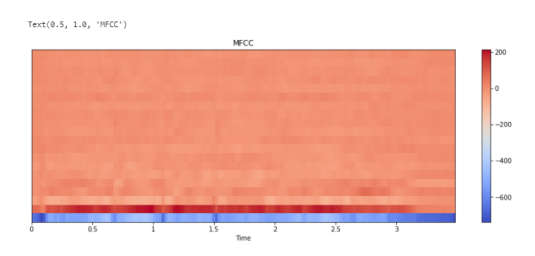

Мел-кепстральные коэффициенты (MFCC) в виде массива numpy:

mfccs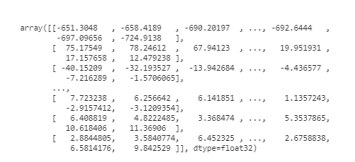

Спектрограмма

Спектрограмма - это визуальный способ представления уровня или “громкости” сигнала во времени на различных частотах, присутствующих в форме волны. Обычно изображается в виде тепловой карты. .stft() преобразует данные в кратковременное преобразование Фурье. С помощью STFT можно определить амплитуду различных частот, воспроизводимых в данный момент времени аудиосигнала.

X = librosa.stft(y)
Xdb = librosa.amplitude_to_db(abs(X))
plt.figure(figsize=(14, 5))
librosa.display.specshow(Xdb, sr=sr, x_axis='time', y_axis='hz')
plt.colorbar()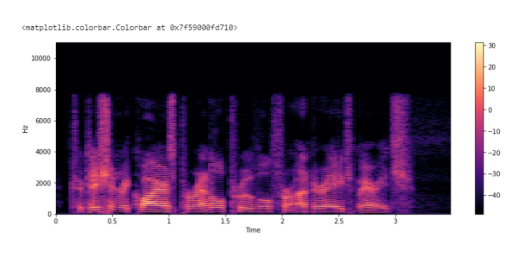

Поскольку все действие происходит в нижней части спектра, мы можем преобразовать ось частот в логарифмическую:

librosa.display.specshow(Xdb, sr=sr, x_axis='time', y_axis='log')
plt.colorbar()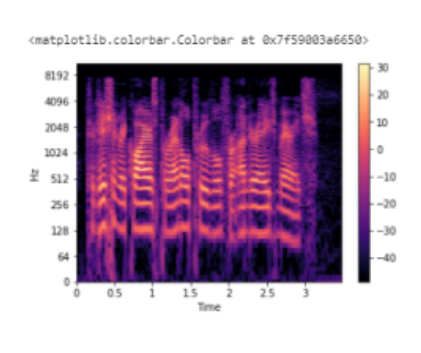

Спектральный центроид - Spectral Centroid.

Указывает, на какой частоте сосредоточена энергия спектра или, другими словами, указывает, где расположен “центр масс” для звука. librosa.feature.spectral_centroid вычисляет спектральный центроид для каждого фрейма в сигнале:

# Spectral Centroid
cent = librosa.feature.spectral_centroid(y=y, sr=sr)
plt.figure(figsize=(15,5))
plt.subplot(1, 1, 1)
plt.semilogy(cent.T, label='Spectral centroid')
plt.ylabel('Hz')
plt.xticks([])
plt.xlim([0, cent.shape[-1]])
plt.legend()

Построение спектрального центроида вместе с формой волны:

import sklearn
spectral_centroids = librosa.feature.spectral_centroid(y, sr=sr)[0]
spectral_centroids.shape

# Вычисление временной переменной для визуализации
plt.figure(figsize=(12, 4))
frames = range(len(spectral_centroids))
t = librosa.frames_to_time(frames)
# Нормализация спектрального центроида для визуализации
def normalize(y, axis=0):
    return sklearn.preprocessing.minmax_scale(y, axis=axis)
# Построение спектрального центроида вместе с формой волны
librosa.display.waveplot(y, sr=sr, alpha=0.4)
plt.plot(t, normalize(spectral_centroids), color='b')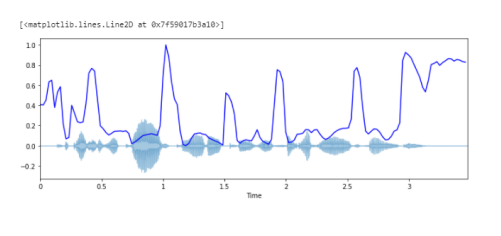

Спектральный контраст - Spectral Contrast

Каждый кадр спектрограммы  S делится на поддиапазоны. Для каждого поддиапазона энергетический контраст оценивается путем сравнения средней энергии в верхнем квантиле (энергия пика) со средним значением энергии в нижнем квантиле (энергия впадины). Высокие значения контрастности обычно соответствуют четким узкополосным сигналам, а низкие значения контрастности соответствуют широкополосным шумам.

# Spectral Contrast
contrast=librosa.feature.spectral_contrast(y=y_harmonic,sr=sr)
plt.figure(figsize=(15,5))
librosa.display.specshow(contrast, x_axis='time')
plt.colorbar()
plt.ylabel('Frequency bands')
plt.title('Spectral contrast')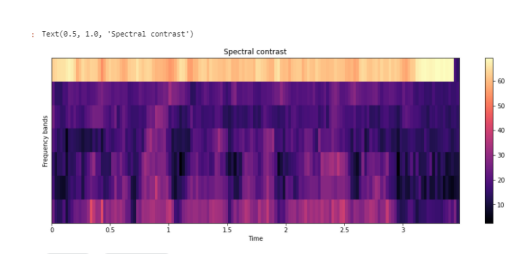

Спектральный спад - Spectral Rolloff.

Это мера формы сигнала, представляющая собой частоту, в которой высокие частоты снижаются до 0. Чтобы получить ее, нужно рассчитать долю элементов в спектре мощности, где 85% ее мощности находится на более низких частотах. librosa.feature.spectral_rolloff вычисляет частоту спада для каждого фрейма в сигнале:

# Spectral Rolloff
rolloff = librosa.feature.spectral_rolloff(y=y, sr=sr)
plt.figure(figsize=(15,5))
plt.semilogy(rolloff.T, label='Roll-off frequency')
plt.ylabel('Hz')
plt.xticks([])
plt.xlim([0, rolloff.shape[-1]])
plt.legend()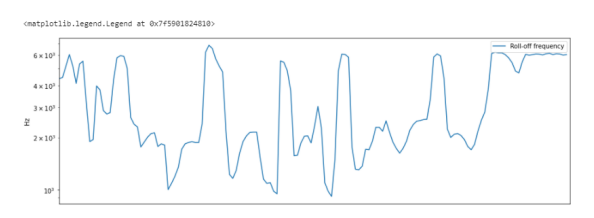

Построение спектрального спада вместе с формой волны:

spectral_rolloff = librosa.feature.spectral_rolloff(y+0.01, sr=sr)[0]
plt.figure(figsize=(12, 4))
librosa.display.waveplot(y, sr=sr, alpha=0.4)
plt.plot(t, normalize(spectral_rolloff), color='r')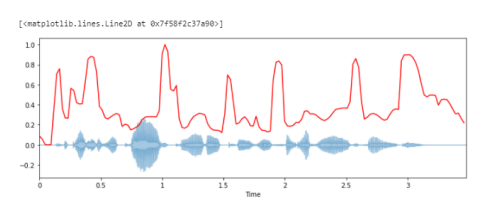

Спектральная ширина - Spectral bandwidth.

Спектральная ширина определяется как ширина полосы света на половине максимальной точки . Спектральная полоса пропускания  в кадре t . Результат - полоса частот для каждого кадра.

spectral_bandwidth_2 = librosa.feature.spectral_bandwidth(y+0.01, sr=sr)[0]
spectral_bandwidth_3 = librosa.feature.spectral_bandwidth(y+0.01, sr=sr, p=3)[0]
spectral_bandwidth_4 = librosa.feature.spectral_bandwidth(y+0.01, sr=sr, p=4)[0]
plt.figure(figsize=(15, 9))
librosa.display.waveplot(y, sr=sr, alpha=0.4)
plt.plot(t, normalize(spectral_bandwidth_2), color='r')
plt.plot(t, normalize(spectral_bandwidth_3), color='g')
plt.plot(t, normalize(spectral_bandwidth_4), color='y')
plt.legend(('p = 2', 'p = 3', 'p = 4'))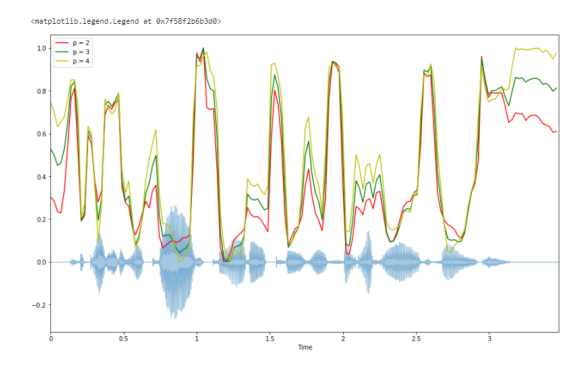

Скорость пересечения нуля - Zero Crossing Rate

Простой способ измерения гладкости сигнала — вычисление числа пересечений нуля в пределах сегмента этого сигнала. Голосовой сигнал колеблется медленно. Например, сигнал 100 Гц будет пересекать ноль 100 раз в секунду, тогда как “немой” фрикативный сигнал может иметь 3000 пересечений нуля в секунду.

# Zero Crossing Rate
zrate=librosa.feature.zero_crossing_rate(y_harmonic)
plt.figure(figsize=(14,5))
plt.semilogy(zrate.T, label='Fraction')
plt.ylabel('Fraction per Frame')
plt.xticks([])
plt.xlim([0, rolloff.shape[-1]])
plt.legend()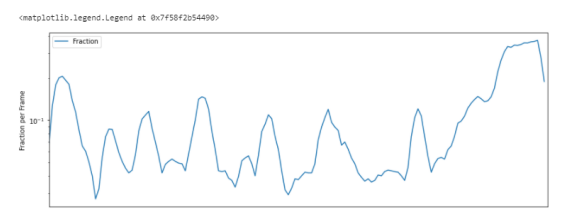

Скорость пересечения нуля - Zero Crossing Rate (увеличенный масштаб):

# Построение графика сигнала:
plt.figure(figsize=(14, 5))
librosa.display.waveplot(y, sr=sr)
# Увеличение масштаба:
n0 = 9000
n1 = 9100
plt.figure(figsize=(14, 5))
plt.plot(y[n0:n1])
plt.grid()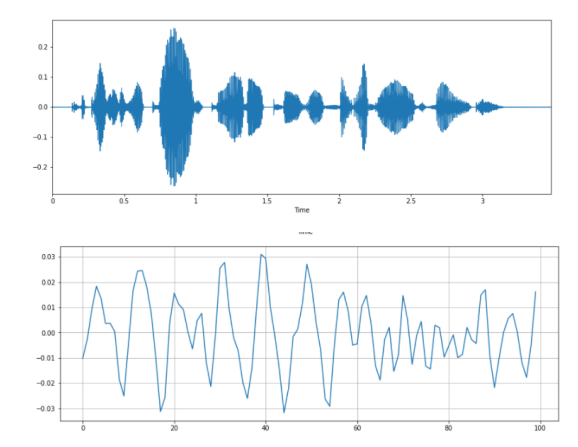

Вычисление числа пересечений нуля:

zero_crossings = librosa.zero_crossings(y[n0:n1], pad=False)
print(sum(zero_crossings))

33

33 пересечения нуля в пределах сегмента этого сигнала.

В следующей (второй ) части анализа аудиоданных разберем:

• Средние значения и стандартные отклонения Мел-кепстральных коэффициентов ( по 20 значений);

• Среднее значение, стандартное отклонение и skew (наклон) Спектрального центроида;

• Среднее значение и стандартное отклонение Спектрального спада;

• Извлечение из Мел-кепстральных коэффициентов - средние значения и стандартные отклонения (по 20 значений);

• Извлечение из Спектрального центроида - среднее значение, стандартное отклонение и skew (наклон);

• Извлечение из Спектрального спада - среднее значение и стандартное отклонение;

• Сохранение значений в формате CSV файла;

• Загрузка данных в Pandas методом read.csv() для дальнейшего анализа фрейма данных (Dataframes - df).