01.06.2022 10:21
Sergey_Kovalenko 1 633 Источник


Перед вами четветая статья-черновик будущей книги «Алгоритмы на кристалле».
В действительности по своему содержанию и стилю изложения ей следовало бы быть первой статьей, не считая оглавление книги и небольшой вводной части. Однако придумать сразу простой подход к изложению удается не всегда. По этой причине лежащий перед текст является во много самостоятельным, его можно читать почти независимо от предыдущих двух статей, обращаясь к ним только как к справочнику. Буду благодарен за любого рода отзвы, как со стороны новичков в этой областти так и тех, кто работает в ней давно — обратная связь поможет сделать финальную редакцию книги лучше.

Предыдущие черновики:
… Примерное оглавление.
… Вычислительная модель.
… Быстродействие логических схем.

Возможно, в вашем браузере с первого раза не будут правильно отображаться формулы. Если так, попробуйте перезагрузит страницу — на моем компьютере этот фокус работает.
Желаю приятного чтения.


Простой способ представить себе работу элементарной логической схемы


Логическая схема и ее компоненты


Логические схемы состоят всего из трех типов компонент: портов (входных и выходных), шин и логических блоков (функциональных и регистров). При графическом изображении логическим блокам соответствуют скругленные прямоугольники, портам — маленькие полукруги, а шинам — тонике, иногда разветвленные линии. Границы самой схемы обозначены прямоугольной рамкой.


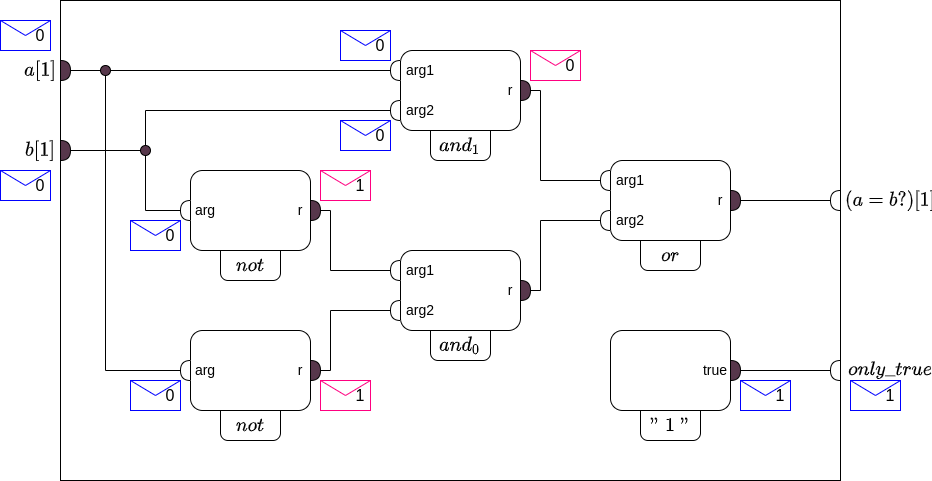
(Схема "=" )
Логическая схема способны производить вычисления, при этом они оперирует двоичными словами: “данными”. Выходные порты (заполненные полукруги) нужны, чтобы отправлять данные, входные порты (белые полукруги) — чтобы их принимать, шины — чтобы передавать данные от выходных портов к входным. Функциональные логические блоки нужны, чтобы данные неким образом преобразовывать, а блоки-регистры — чтобы их временно запоминать.

Пути распространения данных в схеме неизменны: порты статично прикреплены к логическим блокам (внутренние порты) или внешней рамке (внешние порты), шины статично прикреплены к портам. Каждая шина и каждый порт способны работать с двоичными словами строго определённой длины, которая называется их размерностью. Размерности шины и всех прикрепленных к ней портов должны поэтому совпадать. Чтобы избежать неоднозначности в пересылаемых данных, к каждой шине разрешено прикреплять в точности один выходной порт. Места разветвления шин изображаются жирными точками, там, где точек нет — шины всего лишь пересекаются, не оказывая влияния на работу друг друга.

Такт, как эпоха


Процесс вычислений, производимых схемой, состоит из последовательности тактов. Неформально каждый такт удобно представлять себе как продолжительную временную эпоху. Логические схемы проектируются таким образом, чтобы в продолжение каждой эпохи каждый выходной порт смог отправить в прикрепленную к нему шину ровно одно двоичное слово, а каждый входной порт — ровно одно двоичное слово из прикрепленной к нему шины смог принять. Слово, которое на данном такте выходной порт отправит в шину, входной порт примет из шины, а сама шина передаст — будем также называть соответственно значением выходного порта, значением входного порта и значением шины в данный такт времени.

Процесс вычислений в схеме без регистров


По определению значение, которые функциональный блок на данном такте выставит на том или ином своем порту выхода, полностью определяется именем порта выхода, типом блока и значениями, которые на этом такте примут его входные порты. Например, функциональные блоки элементарного типа “+” реализуют сложение двух однобитных чисел: порту "$c$" блок этого типа выставит значение “1” тогда и только тогда, когда оба его входных порта "$arg1$" и "$arg2$" на этом тате приняли значения “1”, а значение порта “$r$” окажется равным “1” лишь в том случае, когда среди значений "$arg1$" и "$arg2$" единица в точности одна. У блоков-констант нет портов входа, на каждом такте своим портам выхода они выставляют одно и тоже значение: блок “ноль” выставляет “0”, блок “единица” выставляет “1”. Спецификация функциональных блоков всех элементарных типов описана в аксиомах E1-E7 статьи “Вычислительная модель”.


(рисунок однобитного +)

И так, пусть все логические блоки в схеме являются функциональными. Опишем работу такой схемы в один из тактов.


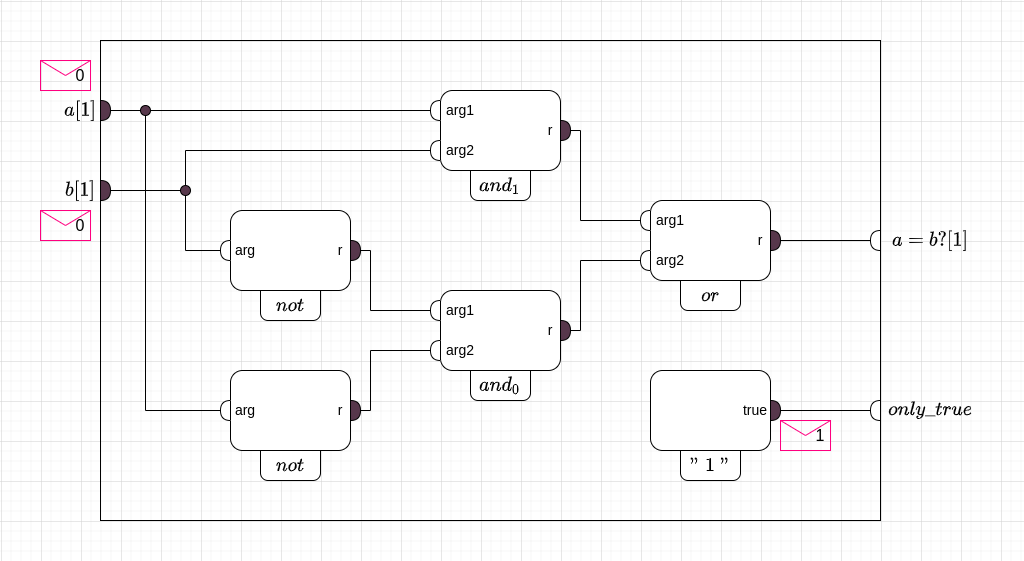
(Cхема равенства с аппендиксом из константы в продолжение одного такта. Начало).

О работе любой схемы мы будем предполагать, что в начале каждого такта значения ее внешних портов уже известны и остаются неизменными до начала следующего такта. Разумеется, известны и также останутся неизменными значения выходных портов всех блоков-констант. Если значение некоторого порта выхода когда-либо стало нам известным, мысленно представим, что затем это значение напечатано на воображаемых конвертах и разослано вдоль прикрепленной к этому порту шине ко всем портам входа, с которыми эта шина соединена.


(Продолжение: рассылка конвертов 1 этап).

Как только каждый входной порт некоторого функционального блока на текущем такте получит свой конверт, мы можем вычислить значения всех выходных портов уже у самого этого блока и тем самым продолжить рассылку конвертов.


(Продолжение: рассылка конвертов 2 этап).

Если в логической схеме нельзя совершить круг, переходя от одного функционального блока к другому функциональному блоку так, чтобы всякий раз при этом один из портов входа второго блока был бы соединен с одним из портов выхода первого, то такая схема называется функционально ациклической (есть в ней регистры, или нет — не важно). Из результатов статьи “Вычислительная модель” следует, что в функционально ациклических схемах (только такие мы и будем рассматриваться в оставшейся части книги) описанный выше процесс рассылки конвертов обязательно приведет к тому, что в итоге каждый входной порт схемы ровно один раз получит свой конверт, а для каждого внутреннего выходного порта, логический блок к которому тот прикреплен, ровно один раз вычислит его значение. Как только это произойдет, очередной такт можно считать завершенным.


(Рассылка конвертов. Конец: все порты получили значения).

Особенности поведения регистров


Элементарные регистры способны хранить в себе однобитные слова — значения регистра. Значения регистров меняются только при смене тактов. Слово, которое появится на единственном выходном порте "$out$" регистра в текущий такт, является копией значения, которое имеет регистр в этот такт времени. То, какое значение будет хранить регистр в следующем такте, полностью определяется настоящим значением регистра и значениями его входных портов, принятыим ими на текущем такте. Все регистры имеют входной порт "$in$", некоторые типы — входные поры "$reset$" и "$enable$" в любых сочетаниях. В зависимости от наличия тех или иных портов и значений, принятых этими портами на текущем такте, значение регистра в следующий такт времени либо сохраняется прежним, либо копирует значение, принятое на текущем такте портом "$in$", либо обнуляется.

Для регистра с одним единственным входным портом "$in$" значение, которое этот регистр будет иметь в следующий такт времени в точности равно значению, которое принял порт "$in$" на текущем такте. Если регистр имеет порт "$reset$" и значение, принятое этим портом на текущем такте есть “1”, то на следующем такте значение регистра станет “0” вне зависимости от других условий.

Чтобы значение регистра можно было сохранять несколько тактов подряд, в некоторые типы регистров добавлен порт "$enable$": без учета влияния порта reset, если на текущем такте порт "$enable$" принял “0”, то значение регистра на следующий такт останется прежним, если “1”, то оно с копирует значение, принятое на этом такте портом "$in$".

Значение любого элементарного регистра в нулевой такт случайно.


(рисунок, поясняющий работу регистров)

Спецификация всех регистров, принятых в этой книге за элементарные, описаны в аксиомах E8-E11 статьи “Вычислительная модель”.

Смена тактов в элементарной схеме


Если в схеме есть регистры, то в начале каждого такта в качестве еще одного первоисточника данных к уже упоминавшимся внешним выходным портам и выходным портам блоков-констант добавляются выходные порты регистров. В остальном процесс вычислений, происходящий на схеме в течение такта почти такой же, что и описанный выше процесс вычислений на схеме без регистров. Единственным отличие будет то, что каждый раз между концом текущего такта и началом следующего все регистры определяют свое новое значение. Ниже приведен пример работы за несколько последовательных тактов простенькой схемы с регистром “пульсар”.



(рисунок, поясняющий работу пульсара в продолжение одного такта)

Замечание по поводу именования портов


Все внешние порты схемы наделяются собственными именами и никакой путаницы в их назывании не будет. В то же время мы неоднократно будем встречать схемы, в которых присутствуют сразу несколько блоков одного и того типа и у каждого из этих блоков есть порт с одним и тем же именем “$A \_port$”. Пусть "$X \_block$" и "$Y \_block$" – собственные имена блоков, обладающих портом с именем “$A \_port$”. Чтобы точно указать о каком именно порте идет речь к имени порта справа через точку будем приписывать собственное имя логического блока, к которому он принадлежит: "$X \_block.A \_port$" – "$A \_port$" блока "$X \_block$", "$Y \_block.A \_port$" – "$A \_port$" блока "$Y \_block$".

На этом наше короткое знакомство с основами теории логических схем закончено. Его объема, в принципе, должно быть достаточно для понимания всего излагаемого ниже материала. Более подробное и формализованное изложение общей теории читатель найдет в двух предыдущих статьях. По мере углубления в предмет их содержание станет полезным. Сейчас мы переходим к конкретным почти промышленным схемам.

Схема каскадного компаратора


Определение старшинства между двоичными словами


Для сравнения двоичных слов мы будем использовать лексикографический порядок. В лексикографическом порядке расставлены слова в словарях и справочниках. Применительно к двоичным словам он определяется следующим образом:

Пусть даны два m-битных слова: $x = x_0, …, x_m-1$ и $y = y_0, …, y_m-1$.
Какое-то число начальных членов этих слов могут быть одинаковыми, то есть: $x_1 = y_1, …, x_i = y_i$. Если эти слова совпадают не во всех позициях и $k$ – наименьшая из позиций, где они отличны, то меньшим считается то слово, у которого на $k$-той позиции стоит «0». Например из двух 7 битных слов «0101000» и «0100111» в лексикографическом порядке второе меньше первого.

В следующем пераграфе мы докажем, что если каждое из слов $x$ и $y$ интерпретировать как запись натурального числа в двоичной системе исчисления: то есть $n(x) = x_0 * 2^{m-1} + …+ x_{m-1} *2^0$, $n(y) = y_0 * 2^{m-1} + …+ y_{m-1} *2^0$, то слово $x$ тогда и только тогда меньше слова $y$ в лексикографическом порядке, кода натурально число $n(x)$, выраженное словом x, меньше натурального числа $n(y)$, выраженного словом $y$ (это утверждение кажется очевидным, но все-таки попробуйте доказать его точно).

Абстрактное описание алгоритма сравнения


Само определение лексикографического порядка содержит в себе алгоритм его вычисления. Действительно, все что мы должны делать — это синхронно перебирать последовательности символов обоих слов до тех пор, пока не обнаружим позицию $k$, на которой символы $x_k$ и $y_k$ различны. То слово, у которого в позиции $k$ стоит 0 и будет меньшим.

В пошаговом виде, описанный алгоритм выглядит так:

  1. Ввести два булевых слова-состояния: первое — “просмотрев символы слов до позиции 0 включительно, установлено, что $x<y$” или коротко — $(x<y)_0$, и второе: “просмотрев символы слов до позиции 0 включительно, установлено, что $y<x$”, коротко — $(y<x)_0$. Обоим словам-состояниям присвоить значение “ложь”, перейти к 2)
  2. Проверить одинаковы ли символы $x_0$ и $y_0$. Если они различны и $x_0 =$ “0”- присвоить значение истина состоянию $(x<y)_0$, если они различны и $y_0 =$ “0” — присвоить значение истина состоянию $(y<x)_0$. Перейти к циклическому повторению 3)-5)
  3. Если рассматриваемая позиция $i$ в словах $x$ и $y$ — последняя, перейти к 7). Иначе в обоих словах перейти к позиции $i+1$, а в алгоритме к шагу 4)
  4. Ввести слова-состояния: слово $(x<y)_{i+1}$ — “просмотрев слова вплоть до позиции $i+1$, установлено, что $x<y$”, и слово $(y<x)_{i+1}$ — “просмотрев слова вплоть до позиции $i+1$, установлено, что $y<x$”. Обоим только что введенным словам-состояниям присвоить значения «ложь». Если хотя бы одно из слов-состояний предыдущей позиции $(x<y)_i$ или $(y<x)_i$ имеет значение «истина» (уже установлено какое из слов меньше), никаких действий над символами $x_{i+1}$ и $y_{i+1}$ не требуется. Просто копируем $(x<y)_i$ в $(x<y)_{i+1}$, $(y<x)_i$ в $(y<x)_{i+1}$. Снова переходим к 3). Иначе переходим к 5).
  5. Если мы здесь, значит анализ $i$ ранее просмотренных позиций слов $x$ и $y$ не смог дать ответ, какое из слов меньше. Сравним текущие позиции $x_{i+1}$ и $y_{i+1}$. Если они различны и $x_{i+1} =$ “0”- присвоить значение истина слову-состоянию $(x<y)_{i+1}$, если они различны и $y_{i+1} = $“0” — присвоить значение истина состоянию $(y<x)_{i+1}$. Вернуться к циклическому повторению шага 3).
  6. Конец алгоритма. Мы просмотрели все m позиций. Логика алгоритма такова, что только одно из слов-состояний: $(x<y)_{m-1}$, или $(y<x)_{m-1}$, может в итоге иметь значение “истина”, тем самым отвечая на вопрос, какое из слов меньше. Если оба этих слова-состояния остались ложными, то слова $x$ и $y$ в точности совпадают.

Интерфейс схемы компаратора


Прежде чем строить схему какого-либо алгоритма, нужно определиться, в каком виде мы собираемся подавать исходные данные, а в каком виде — снимать результат. Компаратор, который мы построим ниже будет способен сравнивать два m-битных слова за один такт. Передаваться эти слова будут в качестве значений внешних выходных $m$-битных портов "$x$" и "$y$". Результат сравнения будет выводится как значения внешних входных 1-битных портов "$(x<y)?$" и "$(y<x)?$", при этом значение “1” будет интерпретироваться как истина, а значение “0” — как ложь. Если оба порта "$(x<y)?$" и "$(y<x)?$" на этом кате имеют значение ложь, значит поступившие на порты $x$ и $y$ в начале этого такта слова идентичны.
image

(интерфейс компаратора)

С интерфейсом схемы мы определились, пора теперь разобраться со знаком вопроса.

Операционная ячейка схемы компаратора


Алгоритм сравнения, который был описан выше, так или иначе синхронно просматривает все позиций слов $x$ и $y$, совершая при этом некоторые действия. Если бы алгоритм был реализован как программа для обычного компьютера, то обработка символов каждой позиции слов $x$ и $y$ выполнялась бы последовательно одним единственным центральным процессором. Реализуя алгоритм в виде логической схемы, мы можем поручить обработку символов каждой позиций отдельной плеяде соединенных между собой логических блоков, которые мы будем называть ячейками (cell). В следующих статьях вы увидите, что такой подход может значительно увеличить производительность вычислительного устройства в сравнении со строго последовательным выполнением алгоритма одним единственным процессором.

В своей логической конструкции описанный выше алгоритм сравнения сводится к следующему:

Находясь над позицией $i$ и наблюдая пару символов $(x_i, y_i)$, мы получаем результат обработки всех предыдущих пар $(x_0, y_0), …, (x_{i-1}, y_{i-1})$ закодированное в значениях однобитных слов-состояний $(x<y)_{i-1}$ и $(y<x)_{i-1}$.

Если одно из этих состояний уже имеет значение “истина”, или же $x_i = y_i$, то все, что надо сделать — это передать без изменений значения обоих этих слов обработчику символов следующей позиции, но уже под видом $(x<y)_i$ и $(“y<x”)_i$.

Если же оба слова $(x<y)_{i-1}$ и $(y<x)_{i-1}$ имеют значение “ложь”, то значения слов-состояний $(x<y)_i$ и $(y<x)_i$ определяется тем, каковы символы $x_i$, или $y_i$. Если эти символы одинаковы, то обеим словам $(x<y)_i$ и $(y<x)_i$ следует приписать ложь. Если же символы различны, то одному из них нужно приписать “истина”, а другому — ложь.

Давайте теперь подробно разберем схемы ячейек-обработчиков.

На рисунке … изображен обработчик пары первых символов слов $x$ и $y$.


(Головная ячейка компаратора)

Плеяда блоков "$dif \_and_in$" (тип "$and$"), "$dif \_not$" (тип "$not$"), "$dif \_or$" (тип "$or$") и "$dif\_and_r$" (обведена сиреневым пунктирным прямоугольником) имеет назначение выяснить, различны ли $x_0$ и $y_0$. Только в том случае, если первые символы слов $x$ и $y$ различны выходной порт "$r$" блока "$dif \_and_r$" посылает в голубую шину значение “1”. Действительно, если значение выходного порта блока "$dif\_and_r$" равно единице, значит и оба его входных порта также на текущем такте приняли значение единица. Порт "$dif \_and_r.arg1$" примет значение “единица”, только если оба символа $x_0$ и $y_0$ одновременно не являются единицей. Далее, порт «dif\_and_r.arg2» будет единицей в точности тогда, когда хотя бы один из символов $x_0$ или $y_0$ является единицей. Вместе два последних предложения доказывают, что "$dif \_and_r.r$" на текущем такте будет иметь значение “1”, только если первые символы поданных в этот такт слов $x$ и $y$ различны.

После того как порт "$dif \_and_r.r$" выдал свое значение, вступают в игру прямые мультиплексоры "$mux_1$" и "$mux_2$". Если первые символы сравниваемых слов одинаковы, то на порты "$comm$" обоих мультиплексоров поступит “0”, соответственно они оба на свой выход скопируют значения своих портов "$arg1$", то есть “0”. Если же символы $x_0$ и $y_0$ различны, значением выходов мультиплексоров станут копии значений их вторых портов входа "$arg2$". В этом случае значением слова $(x<y)_0$ станет копия $y_0$, а значением слова $(y<x)_0$ – копия $x_0$.

Не трудно проверить, что такой способ придавать значения словам $(x<y)_0$ и $(y<x)_0$, когда $x_0$ и $y_0$ не одинаковы, действительно правильно устанавливает какое из слов: $x$ или $y$ меньше в лексикографическом сравнении. Если $x_0 = $«1», то $y_0 = $«0» и слово $(x<y)_0$ копирует $y_0$, то есть получает, как и должно, значение “ложь”, а $(y<x)_0$ копирует $x_0$, то есть получает, как и должно, значение “истина”. Если же $x_0 = $«0», то тогда $y_0 = $«1», соответственно $(x<y)_0$ получает значение “истина”, а $(y<x)_0$ — значение “ложь".

И так, мы доказали, что приведенная схема обработчика двух самых первых символов слов $x$ и $y$ правильно вычисляет слова-состояния $(x<y)_0$ и $(y<x)_0$. Рассмотри теперь обработчик, применимый для всех последующих позиций.


(Регулярная ячейка компаратора)

По сравнению с предыдущим рисунком здесь добавилась плеяда блоков в кирпичном прямоугольнике и блок типа “$and$” "$con \_and$". Одновременно с этим исчез блок-константа и немного поменялись маршруты потоков данных. Самым главным же изменением, которое повлекло все остальные, стало добавление шин, по которым поступают слова-состояния $(x<y)_{i-1}$ и $(y<x)_{i-1}$ от обработчика позиции $i-1$.

При обработке всех позиций, кроме первой, для того, чтобы значения слов $(x<y)_i$ и $(y<x)_i$ не стали простыми копиями $(x<y)_{i-1}$ и $(y<x)_{i-1}$, должны выполняться сразу два условия:

  1. оба слова $(x<y)_{i-1}$ и $(y<x)_{i-1}$ должны иметь значение “ложь”;
  2. значения $x_i$, и $y_i$ должны быть разными.

Второе условие, как и на предыдущем рисунке выполняет плеяда блоков с префиксом "$dif \_$" — она заключена в сиреневый пунктирный прямоугольник. Первое условие проверятся плеядой блоков с префиксом "$s \_$": блоком типа “$or$” "$s \_or$" и блоком типа “$not$” "$s \_not$". Значение выхода блока "$s \_not$" тогда и только тогда равно “1”, когда значение выхода блока "$s \_or$" равно “0”. Последнее будет наблюдаться в том и только в том случае, кода оба слова $(x<y)_{i-1}$ и $(y<x)_{i-1}$ имеют значение “0”.

Блок "$con \_and$" посылает на мультиплексоры “1” только в том случае, если выполнены оба условия. Сценарий, при котором на порты "$com$" мультиплексоров подана “1” ничем не отличается от аналогичного сценария для обработчика головной части: если символы $x_i$ и $y_i$ различны, то значения $(x<y)_i$ и $(y<x)_i$ будут содержать в себе ответ, какое из слов: $x$ или $y$ в лексикографическом порядке меньше другого. Если же на порты "$com$" поданы “0”-ли, то значением выходного порта каждого мультиплексора будет копия значения его входного порта "$arg1$" а слова $(x<y)_i$ и $(y<x)_i$, как и требует алгоритм, будут копиями слов $(x<y)_{i-1}$ и $(y<x)_{i-1}$.

Схема целиком


Давайте теперь объединим все наши наработки в одну схему. Чтобы результат занимал не очень много места перерисуем схемы ячеек в более компактное представление и ограничимся сравнением 3-битных слов. Проверьте самостоятельно, что это все те же самые ячейки-обработчики, которые мы рисовали выше.


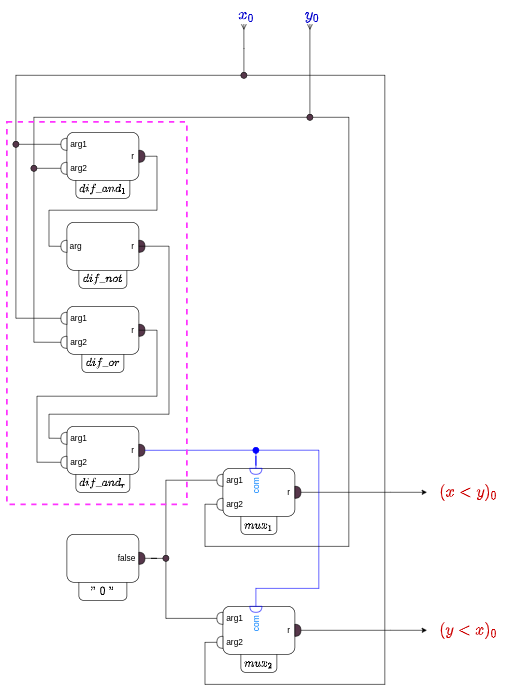
(компактное представление головного обработчика)


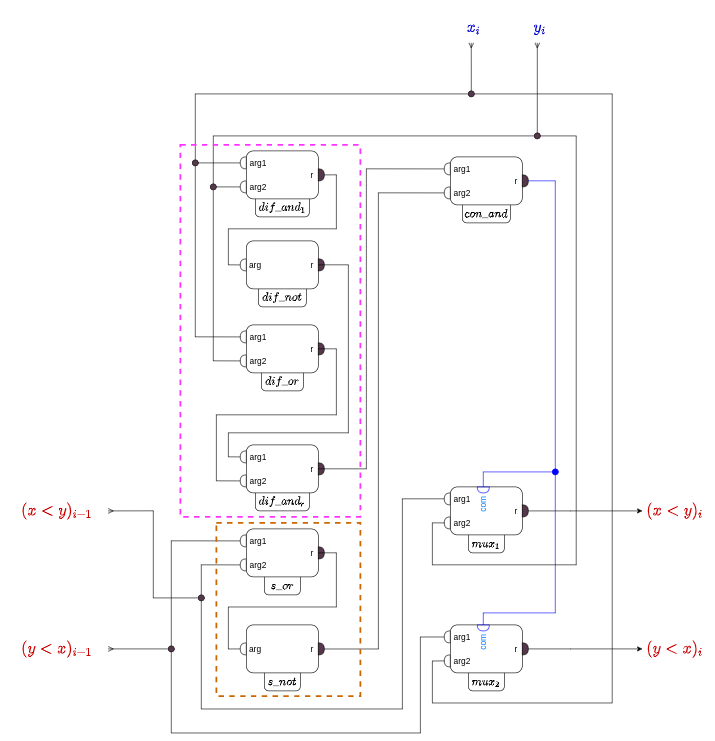
(компактное представление регулярного обработчика)

Остается соединить ячейки между собой и правильно подать на них позиции слов x и y (рис ...). Для разделения 3-битных слов x и y на последовательность их 1-битных символов в схеме используется два блока обратной конкатенации типа "$*^{-1}(1,1,1)$": "${*^{-1}}_x$" и "${*^{-1}}_y$". Мелкие детали схему можно рассмотреть с увеличением, если щелкнуть по ней мышкой.


(схема целиком)

Двоичное представление натуральных чисел


Позиционное исчисление с основанием 2


Всякому двоичному слову $x = x_0, … x_m$ (каждое $x_i$ есть либо 0, либо 1) можно поставить в соответствие натуральное число $n(x)$ по правилу $n(x) = x_0 * 2^m + … + x_m * 2^0$. Сумму членов правой части последнего равенства мы будем называть двоично-степенным разложением числа $n(x)$, а двоичное слово $x$ — двоичным представлением числа $n(x)$, или по-другому — его записью в позиционной системе исчисления с основанием 2. Например, двоичному слову «100» соответствует число $1*2^2 + 0*2^1 + 0*2^0 = 4$. В то же время число “сто” представимо как $64 + 32 + 4 = 2^6 + 2^5 + 2^2$, поэтому оно, например, соответствует двоичному слову «01100100», порождающему двоично-степенное разложение: «сто»$ = 0*2^7 + 1*2^6 + 1*2^5 + 0*2^4 + 0*2^3 + 1*2^2 + 0*2^1 + 0*2^0$.

В этой книге при построении логических схем в основном будет использоваться именно двоичная система исчисления, поэтому часто мы не будем различать само число $n(x)$ и его двоичную запись $x$. Двоичные записи натуральных чисел мы будем называть двоичными (натуральными) числами.

Пусть $n$ — какое-либо натуральное число, а $x_0 * 2^m + x_1 * 2^{m-1} + … + x_m * 2^0 = n$ — какое-либо двоично-степенное разложение $n$ (каждый коэффициент $x_i$ есть либо 1, либо 0). Коэффициент $x_{m-i}$ при i-той степени двойки в этом разложении мы будем обозначать как $p_i = p_i(x)$ — и называть $i$-тым (двоичным)разрядом числа $n$ в его двоичной записи $x$. Согласно последнему определению:
$x_0 = p_m $,
$* $
$x_i = p_{m - i} $
$* $
$x_m = p_0$.

Чуть позже мы покажем, что значение $i$-того разряда числа $n$ одинаково во всех двоичных записях $n$, куда этот разряд входит, и поэтому вместо $p_i(x)$, мы сможем позволить себе писать $p_i(n)$. Например, двоичным представлением числа “один” будут записи “1”, “01”, “001” “0001” — у них у всех значение нулевого разряда есть 1, у тех же записей, в которых есть разряд номер один — его значения одинаково и равно 0, и так дале.

По поводу двоичного представления чисел естественно возникают два вопроса:

  1. Всякое ли натуральное число можно представить в двоичном виде?
  2. Если такое представление у некоторого натурального числа имеется, единственно ли оно?

Ответы на оба этих вопроса многим читателям покажутся очевидными, однако часто наше сознание путает знакомое с понятным. Ниже приведены рассуждения, дающие точный ответ на каждый из вопросов, но для читателя было бы хорошим упражнением попробовать прежде обдумать их самостоятельно.

Существование двоичного представления для любого натурального числа


При помощи математической индукции докажем, что у всякого натурального числа имеется двоично-степенное разложение.

Число 0 представимо так: $0 = 0*2^0$;

Число 1 тоже: $1 = 1*2^0$;

Предположим, что для всех натуральных чисел, меньших $n$ мы уже доказали возможность их представления в двоичном виде, покажем, что и само $n$ тоже можно так представить.

Число n либо четное, либо нечетное.

Если $n$ — четное и $n$ не ноль, то $n/2$ — есть некоторое натуральное число $k$, строго меньшее $n$. По индукционному предположению число $k$ можно представить как $k = x_0*2^m + ... + x_m*2^0$, где каждое $x_i$ есть либо 0, либо 1. Но $n = 2k = 2*(x_0*2^m + ... + x_m*2^0) = x_0*2^{m+1} + ... + x_m * 2^1 + 0*2^0$. Откуда следует, что двоичным представлением $n$ будет, например, двоичная последовательность $y = x_0, ... x_m, 0$.

Если $n$ — нечетное число, то число $(n-1)$ — строго меньше $n$ и является четным. Опять же, по предположению индукции число $(n-1)$ имеет некоторое двоичное представление: $(n-1) = x_0*2^m + ... x_{m-1}*2^1+ x_m*2^0$. Поскольку все, быть может кроме последнего слагаемого в этой сумме заведомо делятся на 2, то $(n-1)$ будет четным тогда и только тогда, когда четным является последнее слагаемое $x_m *2^0 = x_m$, но в таком случае $x_m$ должно быть нулем. Таким образом $(n-1) = x_0*2^m + ... x_{m-1}*2^1+ 0 *2^0$, но тогда $n = (n-1) + 1 = (n-1) = (x_0*2^m + ... x_{m-1}*2^1+ 0 *2^0) + 1 = x_0*2^m + ... x_{m-1}*2^1+ 1*2^0$ — есть двоично-степенное представление числа $n$.

И так, в обоих случаях индукционный шаг сделан и тем самым представимость всех натуральных в двоичном виде может считаться доказанной.

Разложение степеней двойки. Геометрическая интерпретация


Чтобы решить вопрос единственностью, в алгоритме прибавления/вычитания единицы и еще много где, нам понадобится одно замечательное тождество:

$(2^{k-1} + 2^{k-2} + ... + 2^0) + 1 = 2^k $



В принципе это тождество можно доказать, используя школьные знания о сумме членов геометрической прогрессии, но есть и более наглядный способ.

Пусть $k>1$. Представьте $2^k$ одинаковых карандашей, уложенных в ряд и маленький флажок ровно в середине. Этот флажок займет положение аккуратно между острием предыдущего и тупым концом следующего карандаша в их ряду. Число карандашей в ряду слева от флажка будет $2^{k-1}$ штук, справа столько же.



(Слева от флажка $2^2$ карандашей справа столько же)

Если число карандашей в группе слева от флажка больше одного (то есть $2^{k-1} >1$), то переместим флажок в середину этой группы. Теперь слева от флажка $2^{k-2}$ карандаша, а справа $2^{k-1} + 2^{k-2}$.



(Слева от флажка $2^1$ карандаш, справа $2^2 + 2^1$ )

Будем перемещать флажок в середину остающегося от него по левую сторону группы карандашей вновь и вновь до тех пор, пока в ней не останется всего один карандаш. В этот момент справа число карандашей будет выражаться суммой $2^{k-1} + 2^{k-2} + ... + 2^0$. Для завершения доказательства остается только заметить, что общее число карандашей справа и слева от перемещения флажка никак не менялось и по-прежнему равно $2^k$.



(Слева от флажка $2^0 =1$ карандаш, справа $2^2 + 2^1 + 2^0$, всего в ряду $2^3$ карандашей)

Сравнение натуральных чисел в их двоичном представлении


Сейчас мы аккуратно докажем утверждение, которое применительно к десятичным числам воспринимается обычно как самоочевидное. Будем считать, что символ «0» меньше символа «1», тогда справедлива:

Лемма о сравнении двоичных чисел: Пусть $x = x_0 ... x_m$ и $y = y_0, ... y_m$ — двоичные слова одинаковой длины $m$, $n(x) = x_0*2^m + ... + x_m*2^0$ и $n(y) = y_0*2^m + ... + y_m*2^0$ — натуральные числа, которых эти двоичные слова представляют. Число $n(x)$ тогда и только тогда меньше числа $n(y)$, когда в первой слева позиции слов $x$ и $y$, в которой их символы различны, символ слова $x$ меньше, чем символ слова $y$. То есть, если $x_0 = y_0, x_1 = y_1, ..., x_{k-1} = y_{k-1}$, и $k$ — наименьший номер, такой что $x_k \neq y_k$, то неравенство $n(x)<n(y)$ равносильно неравенству $x_k < y_k$

Лемму о сравнении можно переформулировать еще и так: если длины слов $x$ и $y$ совпадают, то число $n(x)$ тогда и только тогда меньше числа $n(y)$, когда по отношению к лексикографическому порядку слово $x$ меньше слова $y$. Таким образом схема компаратора двоичных слов, которую мы построили в предыдущем параграфе, подходит и для сравнения величины двоичных чисел.

Доказательство.
Пусть $x$ и $y$ не совпадают полностью и $k$ — наименьший номер среди тех их позиций, в которых символы этих слов различны. Тогда $x_0 = y_0, x_1 = y_1, ..., x_{k-1} = y_{k-1}$, а значит первые $k$ слагаемых суммы $x_0*2^m + ... + x_m*2^0 = n(x)$ совпадают с первыми $k$ слагаемых суммы $y_0*2^m + ... + y_m*2^0 = n(y)$. Вычеркнем из обоих сумм эти первые $k$ слагаемых — такое действие на знак неравенства все равно никак не повлияет.

Первоначальная задача теперь свелась к необходимости сравнить суммы $x_k*2^{m-k} + ... + x_m*2^0 = n(x')$ и $y_k*2^{m-k} + ... + y_m*2^0 = n(y')$ (слово $x'$ есть последовательность $x_k, ... x_m$, а слово $y'$ есть последовательность $y_k, ... y_m$), причем нам заведомо известно, что $x_k \neq y_k$.

Предположим, что $x_k < y_k$. Последнее неравенство возможно только если $x_k = 0$, а $y_k = 1$, то есть $n(x') = 0*2^{m-k} + x_{k+1}*2^{m-k-1} + ... + x_m*2^0$ и $n(y) = 1*2^{m-k} + y_{k+1}*2^{m-k-1} + ... + y_m*2^0$. Поскольку все коэффициенты $x_i$ и $y_i$ в только что написанных суммах могут быть только нулями и единицами, то $n(x')$ заведомо не превосходит суммы $2^{m-k-1} +... + 2^0 = 2^{m-k} - 1$ (разложение степени двойки), а $n(y')$ заведомо не меньше суммы $1*2^{m-k} + 0*2^{m-k-1} + ... + 0*2^0 = 2^{m-k}$. Очевидным образом $2^{m-k} - 1$ строго меньше чем $2^{m-k}$, откуда следует, что $n(x')$ строго меньше $n(y')$, а значит и $n(x)$ строго меньше $n(y)$.

При симметричном предположении, что что $y_k < x_k$ рассуждения повторяются с точностью до замены буквы $x$ на букву $y$ и наоборот. Если читатель их проделает, то получит, что в этом случае $n(y)$ должно быть строго меньше $n(x)$. Тем самым все случаи (включая полное совпадения $x$ и $y$) нами рассмотрены и доказательство леммы можно считать завершенным.

Следствие (почти однозначность представления): Никакое натуральное число не может иметь двух различных двоичных представлений одной и той же длинны $m$.

Действительно, если два бинарных слова имеют одинаковую длину и различаются, то отыскав самую левую позицию, в которой их символы различны, мы обнаружим, что одно из слов представляет число строго меньшее по сравнению с числом, которое представляет оставшееся слово.

Конечно, отказавшись от требования равенства длин представлений, мы обнаружим, что утверждение о единственности перестает быть верным. Например, число “один” представляют двоичные слова “1”, “01”, “001” и так далее.

Упражнение: докажите, что у всякого натурального числа большего нуля существует в точности одно двоичное представление, первым символом которого является “1”.

Конкатенация двоичных представлений


В математике конкатенацией $x*y$ (не обязательно двоичных) слов $x$ и $y$ называется слово, получающееся приписыванием слова $y$ непосредственно справа от $x$. Например, если $x=$”$abc$”, $y=$”$dfg$”, то $x*y = $“$abcdfg$”, а $y*x = $"$dfgabc$". Еще один пример уже для двоичных слов: $“1111” * ”000” = “1111000”$.

Конкатенация — простое и очень удобное понятие. Любое изложение какой-либо теории, затрагивающее собой формальные слова, без этого термина становится крайне косноязычным.

На формальном языке математики точное определение конкатенации звучит следующим образом: пусть $x = x_0, … x_m$ – цепочка символов длины $m+1$, $y = y_0, … y_n$ — цепочка символов длины $n+1$, тогда $x*y = (x*y)_0, … (x*y)_{m+n+1}$ — цепочка символов длины $m+n+2$, такая что символ $(x*y)_i$ совпадает с $x_i$ в случае, когда $i \leq m$, и совпадает с $y_{i – m - 1}$ в случае, когда $i>m$.

Легко проверить, что операция конкатенации ассоциативна, то есть для любых слов $x$, $y$ и $z$: $(x*y)*z = x*(y*z)$. В то же время конкатенация не коммутативна, если в словах разрешено использовать хотя бы два различных вида символов: $111*000 = 111000 \neq 000111 = 000*111$.
Для дальнейшего изложения нам также будет удобно вести еще несколько специальных определений.

Длину слова $w$, то есть число символов, составляющих w, будем обозначать как $|w|$.
Слово “$00...0$”, составленное из $k$ нулей, мы будем обозначать как $0^k$.
Слово “$11...1$”, составленное из $m$ единиц, мы будем обозначать как $1^m$.
Пустое слово “”, то есть слово, не содержащее ни одного символа, в математик по традиции обозначается греческой буквой $\varepsilon$ (эпсилон). Нам будет удобно считать, что пустое слово также представляет натуральное число: $n( \varepsilon ) = 0$.

Очевидным образом:
$0^p*0^q = 0^{p+q}$;
$1^p*1^q = 1^{p+q}$;
$0^0 = 1^0 = \varepsilon$;
$|0^k| = |1^k| = k$;
$|\varepsilon | = 0$;
для любого слова $x$: $\varepsilon * x = x * \varepsilon = x$;
для любых слов $x$ и $y$: $|x*y| = |x| + |y|$

В отношении того, как конкатенация двоичных слов влияет на величину представляемых этими словами чисел, верна следующая

Лемма о свойствах конкатенации двоичных чисел:

  1. $n(0^k) = 0$ — любая цепочка нулей является двоичным представлением числа ноль;
  2. $n(1^k) = 2^k - 1$ (лемма о разложении степени двойки);
  3. для любого двоичного слова $x$: $n(0^k * x) = n(x)$ (дописывание нулей слева к двоичному представлению, не меняет представляемого им числа);
  4. для любого двоичного слова $x$: $n(x * 0^k) = n(x) * 2^k$ (дописывание к двоичному слову каждого нуля справа увеличивает представляемое им число в 2 раза);
  5. для любых двоичных слов $x$ и $y$$n(x*y) = n(x) * 2^|y| + n(y)$;


Ее доказательство элементарно и предоставляется читателю в качестве еще одного упражнения.

Арифметические действия над двоичными числами


Если двоичное слово x представляет натуральное число, то само это слово мы договорились назвать двоичным числом. Давайте теперь для каждой арифметической операции $op$ над натуральными числами построим ее аналог $op’$ над множеством чисел двоичных. В своих определениях мы будем стремиться к тому, чтобы не было разницы между числом, которое представляет результат выполнения $op’$ над двоичными словами и числом, которое получено
в результате выполнения $op$ непосредственно над числами, которые эти аргументы-слова представляли. Сейчас вам все станет ясно на примере.

Суммой $x + y$ двоичных чисел $x$ и $y$ мы будем считать любое двоичное слово $z$, представляющее число $n(x)+n(y) = n(z)$. Так суммой двоичных чисел «001» и «100» является, например, двоичное число «00101».

Произведением $x*y$ двоичных чисел $x$ и $y$ назовем всякое двоичное слово $z$, представляющее число $n(x)*n(y) = n(z)$. Скажем произведением двоичных чисел «10», представляющего число 2 и «100», представляющего число 4 может считаться двоичное число «1000», поскольку оно представляет число 8.

Двоичное число $x$ считается меньше двоичного числа $y$ тогда и только тогда, когда $n(x) < n(y)$. Из доказанного нами выше следует, что двоичное число $x$ меньше одинакового с ним по длине двоичного числа $y$ тогда и только тогда, когда слово $x$ в лексикографическом порядке меньше слова $y$.

Деление с остатком и разность, когда она возможна, отношения равенства, отношение больше и другие имеют аналогичные определения.

Алгоритмы вычисления сумм, разностей, произведений и частных двоичных чисел почти дословно повторяют знакомые нам со школы алгоритмы выполнения операций “столбиком” над десятичными числами, а в некоторых моментах даже значительно проще них.

Каскадная схема для прибавления и вычитания из числа единицы


Преобразования двоичной записи числа, сопутствующие прибавлению и вычитанию из него единицы


Пусть $x$ – двоичное натуральное число и мы хотим прибавить к $x$ единицу. Как это сделать?

Проще всего прибавлять единицу к числам, оканчивающимся на 0. Легко сообразить, что, если $x = w*”0”$, то $x+1 = w*”1”$ (читатель может проверить это обратившись к двоично-степенному представлению $n(x)$ или воспользовавшись пунктом 5) леммы о конкатенации). Как иллюстрация: $n(“100”) = 4$, $n(“1”) = 1$, $n(“101”) = 5$, поэтому $“100” + “1” = “101”$.

Другой сравнительно простой случай для прибавления единицы — это, когда двоичное число $x$ состоит из одних только единиц, то есть $x = 1^k$. Согласно лемме о разложении степени двойки слово $1^k$ представляет число $2^k- 1$, следовательно слово $x+1$ должно представлять $2^{k-1}$, для чего сгодится, например двоичное число $“1”*0^k$ ( $“111” = 4+2+1 = 8-1$, $“111”+”1” = “1000” = 8$ ).

Рассмотрим теперь произвольное двоичное число $х$, заканчивающееся символом единица, но не состоящее только из одних единиц. Пусть $m$ — длина $x$, а $k+1$ — наименьший по номеру разряд числа $x$, в котором стоит символ “0”. В таком случае слово $x$ можно представить как $x = w*”0”*1^k$, где $w = x_0, … x_{m-k-1}$ (например, двоичное слов «1010111» можно представить как «101»$*$«0»$*$«111»). Следовательно, двоично-степенное разложение $n(x)$ будет иметь вид:

$n(x) = (x_0 * 2^m + … + x_{m-k-1} * 2^{k+1}) + 0*2^k + (1*2^{k-1} + …+ 1*2^0)$,

где внутри вторых скобок стоит двоично-степенное разложение числа $n(1^k)$. Но по лемме о разложении степени двойки $n(1^k) = 2^k - 1$, откуда:

$n(x+1) = n(x) +1 = (x_0 * 2^m + … + x_{m-k-1} * 2^{k+1}) + 0*2^k + (2^k-1) + 1 =$
$= (x_0 * 2^m + … + x_{m-k-1} * 2^{k+1}) + 1*2^k + (0*2^{k-1} + … + 0*2^0) = n(w*1*0^k)$.

Последняя цепочка равенств показывает, что в качестве $x+1$ мы можем взять слово $w*”1”*0^k$.

Утверждение предыдущего абзаца можно доказать и по-другому. Обратимся к лемме о конкатенации и напишем цепочку равенств:

$n(x+1) = n(x) + 1 = n(w*”0”*1^k) + 1 = 2^{k+1}*n(w) + n(“0”*1^k) +1 = $
$= 2^{k+1}*n(w) + 2^k +0 = 2^{k+1}*n(w) + n(“1”*0^k) = n(w*”1”*0^k)$.

Несмотря на длинный формальный вывод, алгоритм прибавления единицы к двоичному числу $x$ имеет короткую и приятную словесную формулировку. Без ограничения общности можно считать, что в слове $x$ есть хотя бы один ноль (в противном случае заменим слово $x$ на равное ему по значению слово $“0”*x$), тогда:

!) Чтобы прибавить к двоичному числу x единицу нужно первый c справа ноль в слове x заменить на единицу, а все стоящие перед этим нулем единицы — на нули.

Пример: $“1010111” + “1” = “1011000”$ (проверьте).

Обсудим теперь как, меняются двоичные числа, когда из них единицу вычитают.
Во-первых, пока мы остаемся в рамках только натуральных чисел, нельзя вычесть единицу из двоичных чисел, представляющих число 0, то есть из двоичных слов, в состав которых не входит ни одной единицы.

В остальном вычитать единицу проще всего из слов, которые на единицу заканчивающихся: для двоичного слова $x$ вида $x=w*1$ в качестве $x - 1$ можно зять слово $w*0$. Доказать последнее утверждение можно либо обратившись к двоично-степенному разложению $x$, либо воспользовавшись леммой о свойствах конкатенации и написав цепочку равенств:

$n(w*”1” - ”1”) = n(w*”1”) - 1 = 2*n(w) + 1 – 1 = 2*n(w) + 0 = $
$= 2*n(w) + n(“0”) = n(w*0)$.

Следующий сравнительно простой случай для вычитания единицы — это слова вида $“1”*0^k$. Поскольку $n(“1”*0^k) = 2^k$, то по лемме о разложении степеней двойки: $n(“1”*0^k - “1”) = n(“1”*0^k ) - 1 = 2^k –1 = n(0*1^k)$. Таким образом в качестве разности $“1”*0^k - “1”$ можно взять слово $0*1^k$.

Осталось рассмотреть проблему вычитания единицы из таких двоичных чисел, которые оканчиваются на 0, но при этом не являются словами вида $“1”*0^k$ и не состоят из одних нулей. Пусть $x$ – такое слово, тогда его можно представить как $x=w*”1”*0^k$. Нетрудно сообразить, что на роль $x-1$ подойдет слово $w*”0”*1^k$ — это можно доказать, как и с прибавлением единицы, обратившись к двоично-степенному разложению $x$, но можно и воспользоваться леммой о конкатенации:

$n(x-1) = n(x) - 1 = 2^{k+1} * n(w) + 2^k – 1 = 2^{k+1} * n{w} + n{“0”*1^{k}} = n{w*”0”*1^k}$.

Мы можем собрать все рассмотренные случаи для вычитания из числа единицы в один алгоритм с простой и короткой формулировкой:

!!) Чтобы вычесть из двоичного числа $x \neq 0$ единицу, нужно первую c справа единицу в слове $x$ заменить на ноль, а все стоящие перед этой единицей нули — на единицы.

Как вы сами видите, алгоритмы вычитания и прибавления к числу единицы очень похожи: каждый из них предписывает заменить на противоположные все символы слова $x$ с правого края вплоть до первого нуля, в случае прибавления, и вплоть до первой единицы, в случае вычитания из $x$ единицы. Из-за этой похожести мы совместим эти две операции в одной логической схеме.

Алгоритм прибавления и вычитания единицы в абстрактном виде


И так, чтобы прибавить или вычесть единицу из двоичного числа $x$, мы должны на каком-то участке от правого края $x$ заменить все символы на противоположные, а вне этого участка оставить их как есть. Алгоритм, который будет выполнять эти преобразования мы выстроим подобно тому, как был построен алгоритм сравнения двух слов.

За изменения в каждом разряде $p_i(x)$ слова $x$ назначим ответственными отдельную плеяду элементарных блоков, или, как мы ее будем еще называть, — операционную ячейка $cell_i$. Теперь нам нужно придумать способ, как сообщить ячейке $cell_i$, следует ли той заменить символ в разряде $p_i$ на противоположный или оставить его как есть. Подобно тому, как это организовано в алгоритме сравнения двоичных слов, потребуем, чтобы команда на изменение или сохранение значения $p_i$ приходила от предыдущей по номеру ячейки $cell_{i-1}$ (теперь $cell_{i-1}$ расположена справа от $cell_i$).

При таком способе организации алгоритма на ячейку $cell_i$ кроме задачи опционального изменения значений $p_i(x)$, ложится еще и ответственность за то, какие команды она пошлет ячейке $cell_{i+1}$. Поскольку прекращение каскада изменений в разрядах слова $x$ во время прибавления и во время вычитания единицы наступают при разных условиях, $cell_i$ должна также получать сведения о том, какая именно из этих двух операций в данный момент выполняется. Что ж, общий эскиз алгоритма мы обговорили, перейдем к конкретной его реализации:

  1. Положить $i=0$. Ввести два однобитных слова-состояния $(+1)_0$ и $(-1)_0$. Если на данном такте к слову $x$ должна быть прибавлена единица, положить $(+1)_0 =$ “истина”, $(-1)_0 = $“ложь”. Если единица должна быть отнята — положить $(+1)_0 = $“ложь”, $(-1)_0 = $“истина”. Перейти к шагу 2.
  2. Ввести два однобитных слова состояния: $(+1)_{i+1}$, имеющего смысл — “идет прибавление единицы, разряд $p_{i+1}$ должен быть преобразован”, и $(-1)_{i+1}$, имеющего смысл — “идет вычитание единицы, разряд $p_i$ должен быть преобразован”.

    Присвоить словам $(+1)_{i+1}$ и $(-1)_{i-1}$ значение по умолчанию “ложь”. Если $(+1)_i = $ “истина” и $p_i(x) = “1”$, то исправить значение $(+1)_{i+1}$ на “истина”. Если $(-1)_i =$ “истина” и $p_i(x) = “0”$, то исправить значение $(-1)_{i+1}$ на “истина”.

    Если хотя бы одно из слов-состояний $(+1)_i$ или $(-1)_i$ имеет значение истина, изменить символ в разряде $p_i$ слова $x$ на противоположный. Перейти к шагу 3.
  3. Если $p_i$ — самый большой разряд в $x$, то алгоритм завершен. Значения слов состояний $(+1)_{i+1}$ и $(-1)_{i+1}$ в таком случае трактуются как “произошло переполнение в результате операции +1” и “производилось недопустимое вычитание 1 из нуля” соответственно.

    Если $p_i$ — не последний разряд в $x$, то увеличить $i$ на единицу и вернуться к шагу 2.


Интерфейс логической схемы прибавления/вычитания единицы


Ниже мы построим схему способную на каждом такте прибавлять или вычитать единицу к текущему $m$-битному значению ее внешнего порта выхода $“x”$. Результат будет выведен на внешний $m$-битный входной порт $“(x \pm 1)”$. Какая именно операция будет выполнятся на данном задается с помощью текущих значений внешних однобитных выходных портов “(+1)” и “(-1)”. Чтобы результат был корректны, не более чем одному из портов $“(+1)”$ и $”(-1)”$ разрешено иметь значение “1”. Если оба этих порта имеют значение “0”, то значением порта $“(x \pm 1)”$ окажется само $x$. Случаи, когда единица вычитается из нуля, или для записи числа x+1 не достаточно m разрядов, отслеживаются внешними однобитными входными портами $“too \_small”$ и $“too \_big”$: если значение одного из них “истина”, значит произошла соответствующая ошибка и результат в $“(x \pm 1)”$ не корректен.

image

(интерфейс)

Перейдем теперь к внутренней архитектуре схемы.

Операционная ячейка


Схема операционной ячейки, представленная на рисунке …, разделена пунктирными прямоугольниками на две зоны: верхнюю — внутри кирпичного цвета прямоугольника, и нижнюю — внутри прямоугольника сиреневого цвета. Блоки нижней зоны отвечают за преобразование i-того разряда слова $x$, а блоки верхней — за формирования слов-команд для следующей по номеру операционной ячейки. Рассмотрим каждую зону подробно.


Начнем с нижней. Слова-команды $(+1)_i$ и $(-1)_i$, посланные предыдущей ячейкой поступают на входные порты блока “$or$”. Если хотя бы одно из этих слов имеет значение “истина”, блок “$or$” посылает на входной порт “$com$” мультиплексора "$mux_d$" значение “1”, в противном случае на этот порт приходит ноль “0”.

Блок “$not$” преобразует поступивший на его вход символ разряда $p_i(x)$ в противоположный, а результат посылает на вход "$arg2$" мультиплексора “$mux_d$”. В свою очередь, на "$arg1$" того же мультиплексора подается $p_i(x)$ в неизменном виде. Таким образом, если на текущем такте значение порта “$mux_d.com$” равно нулю, то $i$-тый разряд слова $(x \pm 1)$ будет копией $i$-того разряда слова $x$. В противном случает случае символом зазряда $p_I(x \pm 1)$ станет символ, противоположный $p_i(x)$.

Переходим к верхней зоне. Сюда входит “генератор лжи” — “0” и два прямых мультиплексора: "
"$mux_m$" и "$mux_p$", выходы которых формируют слова-команды $(-1)_{i+1}$ и $(+1)_{i+1}$. Давайте проверим, что значения эти слов получаются правильными.

Рассмотрим работу мультиплексора “$mux_m$”, отвечающего за команду $(-1)_{i+1}$. В зависимости от значения, полученного входным портом "$mux_m.com$", мультиплексор "$mux_m$" выбирает, какое из слов станет значением его выходного порта “$r$”: слово $(-1)_i$ на его входе “$arg1$”, или слово “0” на его входе “$arg2$”.

Когда $(-1)_i = “0”$, выбор не имеет значения: поскольку в этом случае, как и требует алгоритм, значение $(-1)_{i+1}$ все равно окажется нулем, то есть “ложью”. Осталось проверить правильность формирования $(-1)_{i+1}$ в условиях, когда $(-1)_i$ имеет значение “истина”.

В соответствии с описанным нами выше алгоритмом слово $(-1)_i$ будет принимать истинное значение в точности тогда, когда идет процесс вычитания из слова $x$ единицы и этот процесс требует, чтобы символ в разряде $p_i(x)$ был изменен на противоположный. Как говорит нам все тот же алгоритм, каскад изменений разрядов $x$, связанных с вычитанием из него единицы, должен обрываться на первой в $x$ единице справа. Проверим, что ровно так и действует наша ячейка.

Значением порта “$mux_m.com$” является копия символа в разряде $p_i(x)$. Если $p_i(x) =”1”$, мультиплексор “$mux_m$” копирует на выход “$mux_m.r$” значение своего входного порта “$arg2$”, то есть “ложь”. Как и требуется, в этом случае $(-1)_{i+1}$ получает значение “ложь”, тем самым обрывая каскад изменений. Если же $p_i(x) = “0”$, порт “$mux_m.r$” копирует значение порта, “$mux_m.arg1$”, то есть слово $(-1)_i$, которое по предположению выражает истину и, как того и требует алгоритм, каскад изменений разрядов $x$ продолжается.

Анализ правильности установления мультиплексором “$mux_p$” значений слова $(+1)_{i+1}$ проводится аналогично и предоставляется читателю.

Схема целиком


Чтобы получить полный чертеж схемы, реализующей прибавление/вычитание единицы из m-битного числа x, нам остается только соединить в каскад m описанных выше операционных ячеек и правильно подключить их к внешним портам. Как и в схеме компаратора, для разделения m-битного x на однобитные разряды мы применим блок обратной конкатенации $*^{-1}(1^m)$. Для объединения полученных на выходах ячеек m однобитных разрядов $p_i(x \pm 1)$ в одно m-битное слово $(x+1)$ используем блок прямой конкатенации $*(1^m)$. Вся схема целиком изображена на рисунке ниже.


Примерный план следующей статьи.


Составные блоки как обозначения фрагментов схемы.
… Проблема неинформативного дублирования.
… Сравнение работы фрагмента схемы с работой блока.
… Блок клок, который ничего не делает, наглядное преобразование фрагмента в блок.
… Использование готовых схем в качестве составных блоков в неэлементарных схемах
(пример с мультиплексором, рекурсивное определение компаратора и схемы \pm 1)
....K-битные массивы регистров и мультиплексоров.
… Схема “часы”.

Упрощенный взгляд на латентность схемы.
… Взгляд на работу блока как на преобразователь данных.
… Задержки в самом длинном пути.

Прямое, обратное и обоюдонаправленное адресное дерево.
… Адресное дерево как обобщение многоходового мультиплексора (интерфейс).
....K-битные массивы регистров и мультиплексоров.
… Развернутый чертеж n-битного k-ходового дерева для k=8 и k=7.
… Рекурсивное определение. Глубина.
… Замечание об энергоэффективности.
… Однопортовая пользовательская RAM.

Простейшие стеки
… Цепочка сдвиговых регистров и цепочка регистров задержки.
… Цепочка с возможностью извлечения данных.
… Идеальный абстрактный стек и абстрактный стек конечной длины, интерфейс схемы.
… Интерфейс и реализация одной ячейки памяти простейшего стека.
… Схема целиком, рекурсивное определение.
… Устройства контроля опустошения и наполнения с использованием счётчика.

Каскадная очередь.
… Абстрактное определение идеальной очереди, очередь конечного объема.
… Идея реализации на основе стека.
… Контроль точки записи.
… Управление одной ячейкой памяти очереди.
… Схема целиком, рекурсивное определение.

Каскадный сумматор двух k-битных чисел.
… Алгоритм сложения столбиком для двоичных чисел.
… Интерфейс и реализация ячейки, обрабатывающий i-тый разряд.
… Интерфейс и реализация всего устройства.
… Рекурсивное определение, оценка глубины и объема.
… Двухтактный сумматор

Комментарии (1)


  1. Sergey_Kovalenko Автор
    01.06.2022 19:01
    #24399968

    Нельзя ли починить время публикации? Опубликована в 18.49 где-то - на сайте отображается как опубликованная в 10.21. После устранения проблемы комментарий можно удалить.