
В предыдущей статье мы познакомились с терминами и определениями теории графов. В этой же статье обсудим различные способы представления графа в памяти компьютера для его обработки. Покажем, какие структуры данных можно использовать, а также проговорим преимущества и недостатки каждого способа.

Допустим, у нас есть неориентированный граф G из V = 5 вершин и E = 6 рёбер. Вершины пронумерованы от 1 до 5, рёбра для удобства также пронумеруем буквами a, b, c, d, e. Одна вершина с петлёй, изолирована от других.
Перечисление множеств
По определению, граф - это топологическая модель, которая состоит из множества вершин и множества рёбер, их соединяющих. Значит, самый “простой” способ представить граф - определить оба этих множества.

Лично мне ни разу не доводилось видеть алгоритм обработки графа, который бы использовал такой способ хранения вершин и рёбер.
Недостаток такого подхода: использование достаточно тяжеловесной структуры – хэш таблицы – для хранения множества, когда проще и быстрее работать с обычными массивами или списками, к тому же, во множестве нет возможности получить перечисление вершин в порядке их добавления (особенность хэш-таблицы).
Кстати, сами вершины обычно вообще отдельно не хранятся, а указывается только их количество V, они автоматически принимают номера от 0 до V-1. Для хранения цвета / веса или других характеристик вершин можно использовать параллельные массивы для каждого критерия.
Матрица смежности
Это самый популярный и расточительный способ представления графа в памяти. Его уместно использовать, если количество рёбер велико, порядка V2.
Для хранения рёбер используется двумерная матрица размерности [V, V], каждый [a, b] элемент которой равен 1, если вершины a и b являются смежными и 0 в противном случае.
В случае неориентированного графа матрица является симметричной относительно главной диагонали, а сумма каждой строчки и каждого столбца равна степени вершины. В связи с этим, при записи рёбер-петель в матрицу необходимо записывать число 2.

Сложность по памяти: O(V2).
Сложность перечисления всех рёбер: O(V2).
Сложность перечисления всех вершин, смежных с а: O(V).
Сложность проверки смежности вершин a и b: О(1).
Матрица инцидентности
Это самый расточительный способ хранения графа, его уместно использовать, если количество рёбер невелико.
Для хранения используется двумерная матрица размера [V, E], в каждом столбце которой записано одно ребро таким образом: напротив вершин, инцидентных этому ребру, записаны 1, в остальных случаях 0.
Таким образом, сумма чисел в каждом столбце равна 2, а сумма чисел в строчке a равна степени вершины а.

Сложность по памяти: O(V x E).
Сложность перечисления всех рёбер: O(V x E) - хоть каждое ребро и хранится в отдельном столбце, но для получения информации об инцидентных ему вершинах нужно перебрать все числа в столбце.
Сложность перечисления всех вершин, смежных с а: O(V x E).
Сложность проверки смежности вершин a и b: O(E) - достаточно пройтись по строчкам a и b в поисках двух единиц.
Перечень рёбер
Если из матрицы инцидентности убрать все нули, в каждом столбце останется только два числа для каждого ребра - номера инцидентных ему вершин. То есть, для перечисления рёбер достаточно составить список из пар чисел, это очень экономный способ: каждое ребро хранится один раз, когда во всех других вариантах каждое ребро, как правило, записывается дважды.
Недостаток - при поиске вершин в списке рёбер нужно выполнять по две проверки - сравнивать и первую вершину, и вторую.

Сложность по памяти: O(E).
Сложность перечисления всех рёбер: O(E).
Сложность перечисления всех вершин, смежных с а: O(E).
Сложность проверки смежности вершин a и b: О(E).
Список рёбер можно сгруппировать по вершинам, что позволит ускорить поиск смежных вершин. У нас получится ещё три очередных способа, которые очень похожи друг на друга, отличаются лишь способом записи векторов.
Векторы смежности
Для записи вектора смежности используется двумерная матрица размером [V, S], где S - максимальная степень вершины в графе.
В каждой строчке a записаны номера вершин, смежных с а, после чего записаны нули (несуществующие номера вершин).

Сложность по памяти: O(V x S).
Сложность перечисления всех рёбер: O(V x E)
Сложность перечисления всех вершин, смежных с а: O(Sa) (Sa = степень вершины а) = O(E)
Сложность проверки смежности вершин a и b: О(Sa) = O(Sb) = O(E)
Массивы смежности
Для экономии памяти, используется ступенчатый массив, длина каждой строки равна степени данной вершины.
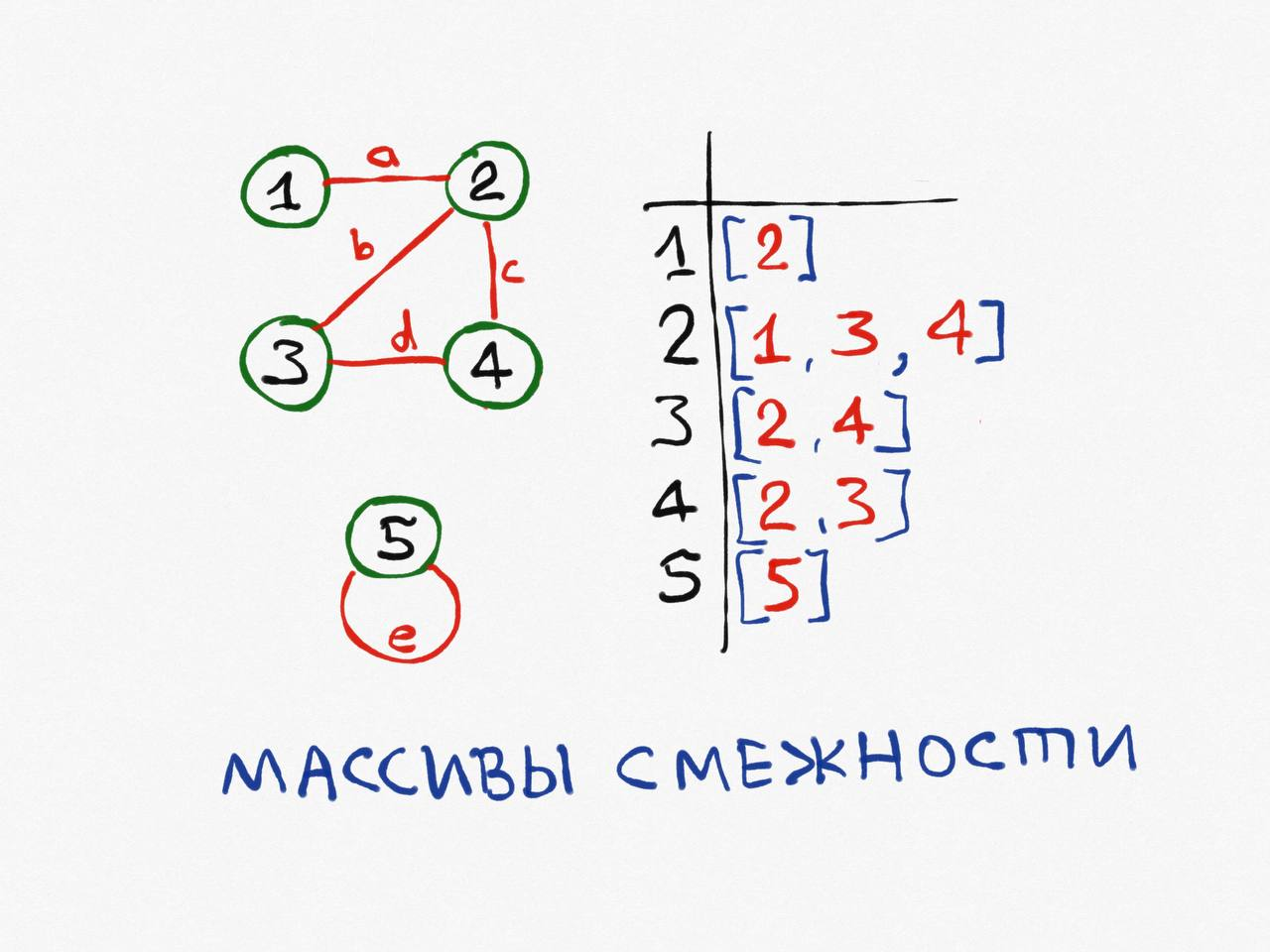
Сложность по памяти: O(сумма степеней всех вершин) = O(E).
Списки смежности
Здесь используется односвязный список для перечисления всех смежных вершин.

Сложность по памяти: O(V + сумма степеней всех вершин) = O(V + 2xE) = O(V + E)
Структура с оглавлением
Один из самых экономных способов представления графа в памяти. Фактически, мы записываем все массивы смежности в одну строчку, в один линейный массив, и создаём массив-оглавление, с указателями на начало списка для каждой вершины.

Сложность по памяти: O(V + сумма степеней всех вершин) = O(V + E).
Список вершин и список рёбер
Самый экстравагантный способ хранения графа.
Вершины записываются в односвязных список, от каждой вершины есть указатель на список всех рёбер, инцидентных данной вершины. Каждое ребро, в свою очередь, имеет указатель на вторую инцидентную ей вершину и на следующее ребро.

Получается весьма разветвлённый граф для представления графа.

Сложность по памяти: O(V + сумма степеней всех вершин) = O(V + E).
Сложность перечисления всех рёбер: O(V x E)
Сложность перечисления всех вершин, смежных с а: O(Sa) (Sa = степень вершины а) = O(E)
Сложность проверки смежности вершин a и b: О(Sa) = O(Sb) = O(E)
Теперь, когда мы знаем способы представления графа в памяти компьютера, можем выбирать наиболее приемлемые варианты для каждой конкретной задачи.
На курсе «Алгоритмы и структуры данных» мы рассматриваем следующие алгоритмы в модуле “Теория графов”: поиск вширь и вглубь, топологическая сортировка (Кана, Таряна, Демукрона), поиск компонент сильной связности (Косарайю), поиск минимального скелета (Прима, Краскала, Борувки), поиск кратчайшего пути (Флойда-Уоршалла, Баллмана-Форда, Дейкстры), алгоритм Джонсона для поиск кратчайшего пути в орграфе с отрицательными дугами (см. мою статью), решение задачи коммивояжера (ближайшего соседа, кратчайшего ребра, ближайшего посредника) и вишенка на торте - алгоритм А* звезда поиска кратчайшего пути с эвристической функцией.
Также хочу пригласить всех желающих на бесплатный демоурок по теме «Дерево отрезков - быстро и просто». Зарегистрироваться на урок.
Комментарии (15)

zuko3d
08.07.2022 03:12+3Если кого-то (как и меня когда-то) заинтересует вопрос, "а есть ли что-то более эффективное?" рекомендую почитать вот эту статью: Log(Graph): A Near-Optimal High-Performance Graph Representation (ethz.ch)

Refridgerator
08.07.2022 06:42+2А в иллюстрации к «Перечень рёбер» случайно нет ошибки? Там "[4,4] e", хотя вроде бы должно "[5,5] e".

Refridgerator
08.07.2022 06:45+1А в «Векторы смежности» непонятно, почему вершина 2 смежна с 1 и 3, а с 4 — уже нет.

Akina
08.07.2022 10:00+1Матрица смежности: Для хранения рёбер используется двумерная матрица размерности [V, V], каждый [a, b] элемент которой равен 1, если вершины a и b являются смежными и 0 в противном случае.
Не учтены кратные рёбра.
Векторы смежности, Массивы смежности:
А куда делись сведения о ребре "c" для вершины 2?

FFormula Автор
08.07.2022 10:43Благодарю, исправлено.
Для кратных ребер значение увеличивается +1

Akina
08.07.2022 12:12Количество кратных рёбер в общем случае - не ограничено. Так что +1 может быть недостаточно.
Тогда должно быть не "каждый [a, b] элемент которой равен 1", а что-то типа "каждый [a, b] элемент которой равен количеству кратных рёбер между этими вершинами, и соответственно для смежных вершин больше нуля, а для не-смежных вершин равен нулю".

EchoA
08.07.2022 10:32+1Спасибо огромное за труд! Как раз собирался искать эту информацию, а тут и вы подоспели =)

OlegZH
08.07.2022 12:04+1В качестве приглашения на курс статья выглядит следующим образом: Вы хотите разобраться в алгоритмах на графах — приходите — мы Вам всё подробно расскажем. Если не сможете, то, всё-равно, приходите.
А на самом деле, графы — это слишком обширная тема. Имеются, даже, довольно толстенные книжки, вроде нашего Евстигнеева или (у них) Сэджвика...
Крайне интересно было бы сравнить различные способы представления графов. Здесь, даже, крайне интересно покрутить самые расточительные по расходу памяти способы (вроде "списка рёбер и вершин"). Посмотреть, как это делается на различных языках программирования. И привести какие-нибудь любопытные и познавательные примеры применения.
Ну и, конечно, вопрос визуализации графов.

klirichek
08.07.2022 18:42Лично мне ни разу не доводилось видеть алгоритм обработки графа, который бы использовал такой способ хранения вершин и рёбер.
На самом деле, в dot/graphviz именно такой способ используется. Сырые данные запихиваются как множества, причём в свободном стиле можно сперва перечислить вершины, потом рёбра, или запихнуть вперемешку.
Конечный результат - единственная картинка; цели оптимизировать её отрисовку по скорости практически нет.
А генерить в связи с простотой очень удобно программно, иногда прямо в url - выплюнул структуру в лог, там ткнул, и в браузере открылась вполне сносная визуализация.
ilmarin77
08.07.2022 22:36Матрица смежности
Это самый популярный и расточительный способ представления графа в памяти
Если использовать разреженную матрицу (sparse matrix), то не расточительный.

Dasfex
10.07.2022 00:33Что-то вы немного странной инфы накрутили.
Векторы смежности и массивы смежности кмк идиоматически должны быть наоборот: чаще всего в языках программирования массивы статического размера, тогда как векторы динамического.
Вообще векторы смежности и списки смежности почти всегда (на самом деле по опыту всегда, ни разу не слышал разделения на массивы/векторы/списки смежности) называются списками смежности. А как вы их реализуете (через векторы, массивы или списки) уже детали. Структура с оглавлением по факту тот же список смежности, только опять же реализованный неким другим образом.
Кажется, во всех алгоритмических вопросах достаточно понять концепцию, а реализовывать исходя из нужд задачи. Тут же получается, что новичок, прочтя вашу статью, станет пытаться вникнуть во все описанные подходы, что может только запутать из-за их большого количества. Хотя по факту, описав лишь концепции, можно было бы сократить статью вдвое. И это позволило бы накинуть больше информации о том, когда те или иные подходы оказываются полезными, а когда нет.


gloomyBrain
Отличная статья, спасибо!