На написание этой статьи меня сподвигла одноименная статья на хабре: "Беги, муравей. Беги". В ней рассматривается решение задачи коммивояжёра  в среде AnyLogic.

О самой задаче можно почитать здесь:  Задача коммивояжёра.  

Если кратко, то задача сводится к нахождению самого короткого пути обхода набора точек (городов) на карте. Решение методом перебора не является эффективным, поскольку количество вычислений огромно. Например, для 15 точек существует 43 миллиарда маршрутов, а для 18 точек (городов) уже 117 триллионов!!!

AnyLogic – среда, предназначенная для решения логистических задач с использованием моделей агентов. Мне показалось интересным, что несмотря на «заточенность» среды на агентное моделирование, при создании модели приходится писать достаточно много кода. Поэтому возникла идея: попробовать реализовать подобную модель, используя среду структурного моделирования, в виде графических функционально-блочных диаграмм. Я уже приводил примеры, как можно реализовать принципы объектно-ориентированного программирования (ООП) в графическом языке программирования.  См. "Объектное ориентированное программирование в графических языках". Здесь же мы попробуем реализовать агентное моделирование средствами системной динамики. 

Дальше будем много хардкороного программежа. Поэтому слабонервным, беременным, девушкам обоего пола, кормящим матерям лучше не читать, во избежание родимчика, свинки и чумки!

Погнали!

В нашей модели будет два класса объектов:

 «Города» - точки на карте, которые нужно посетить.

«Муравьи» - агенты, которые будут бегать между городами в поисках кратчайшего пути. 

Такое странное сочетание объектов вызвано тем, что «Задачу коммивояжера» мы решаем методом «Муравьиной тропы». 

Создаем города

Начнем рисовать прямо в окне проекта, создавая объекты-города. Напомню, что для реализации методов ООП в графическом языке нам необходимо создать структуры данных. Для этого мы используем базу данных сигналов. 

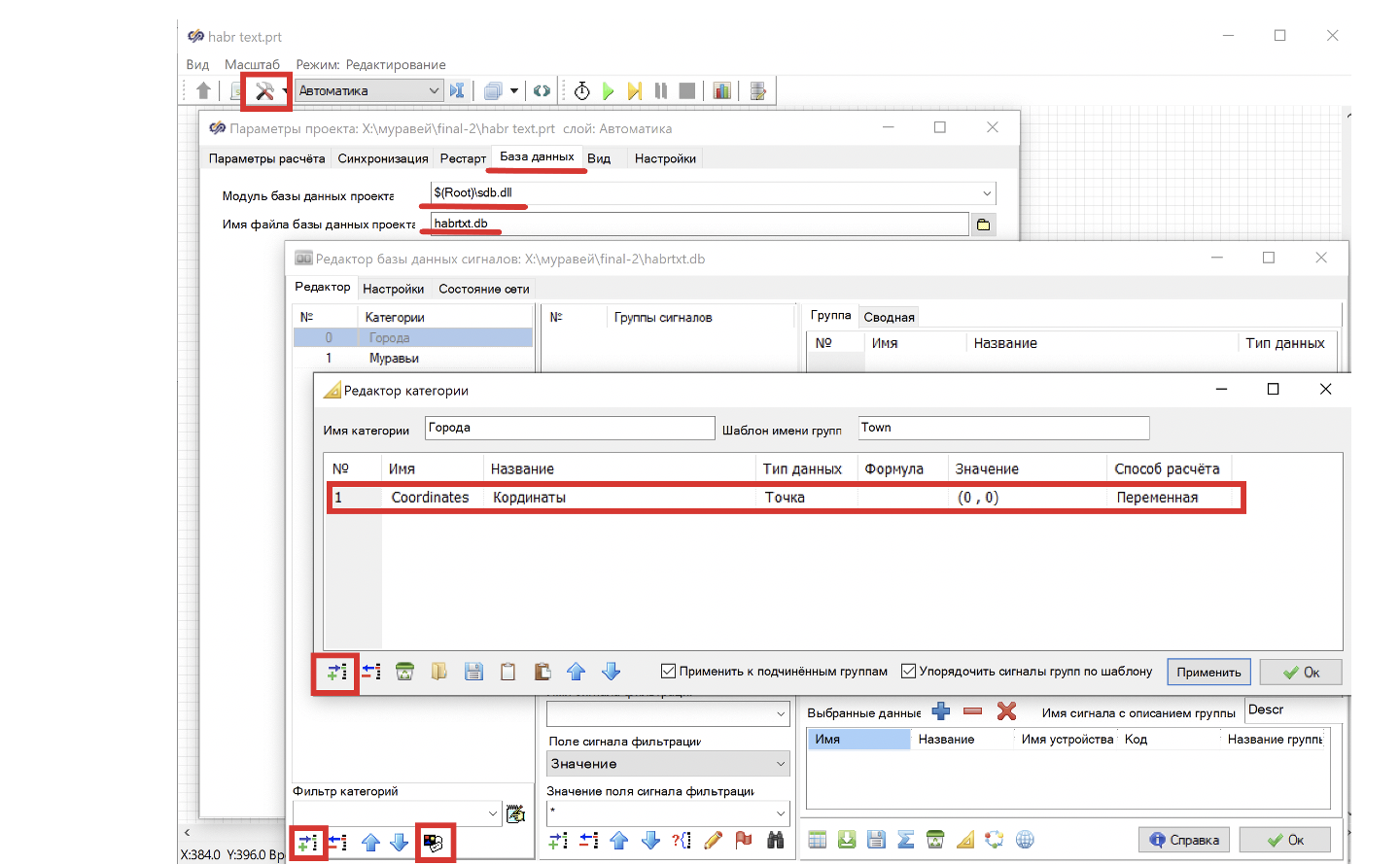
Добавляем к проекту базу данных сигналов c произвольным названием, например «habrtxt.db» (см. рис.1)

Для объекта «город» нам необходимо знать его положение и на этом пока все. Создаем новую категорию «Города», в которую добавляем одно поля:

 «Coordinates» тип данных - Точка. (см. рис. 1):

Непосредственно города будем создавать с помощью языка программирования, аналогично примеру в исходной статье. 

Для начала создадим 100 городов, случайно разбросанных на поле 400х400, и добавим на схему изображение этих городов. Количество городов зададим в качестве константы TownCount, которую в дальнейшем можно будет менять.

Для работы с классами мы используем систему кодирования для создания имен объектов в базе данных сигналов и объектов отображения. В данном примере система кодирования проста, как 3 копейки: имя города состоит из общей части Town и порядкового номера данного города в системе. Town1, Town2, и т.д.

В цикле от 1 до  TownCount мы создаем имена для городов, формируем случайным образом координаты города X,Y.  Создаем из них переменную типа: точка - TownCenter и добавляем новый объект в базу данных сигналов.

Для отображения города мы используем те же координаты случайным образом. Изображением города у нас будет просто закрашенный кружок диаметром 5 единиц. Для создания данного кружка в системе нам необходимо две точки. Точка центра, и точка для определения радиуса (соответствующие переменные - TownCenter, RPoint), [AK1] поэтому мы из центральной точки создаем еще одну, путем добавления радиуса.

Создание городов мы осуществляем на этапе инициализации, который выполняется один раз во время старта расчета. Поэтому весь цикл помещен в секцию инициализации (см. рис.2)

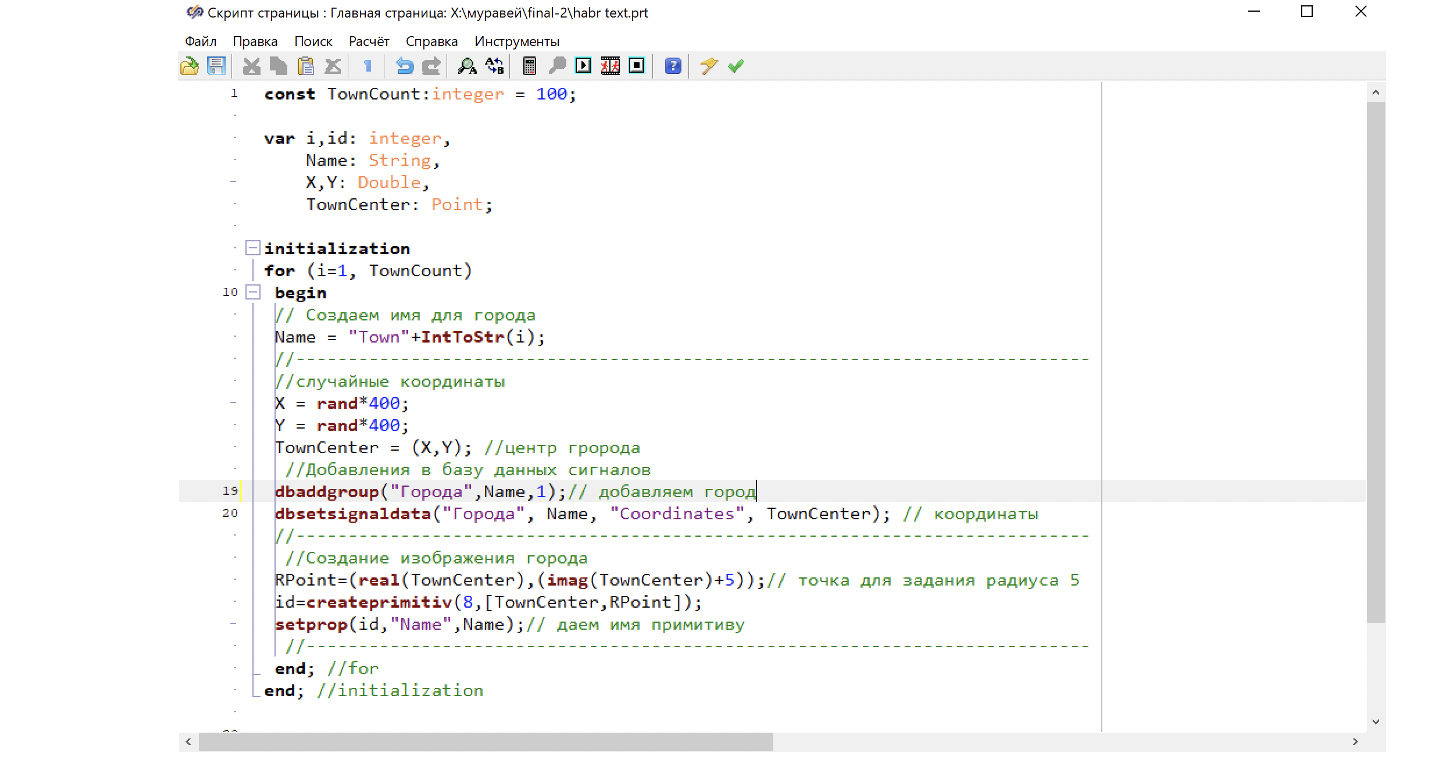
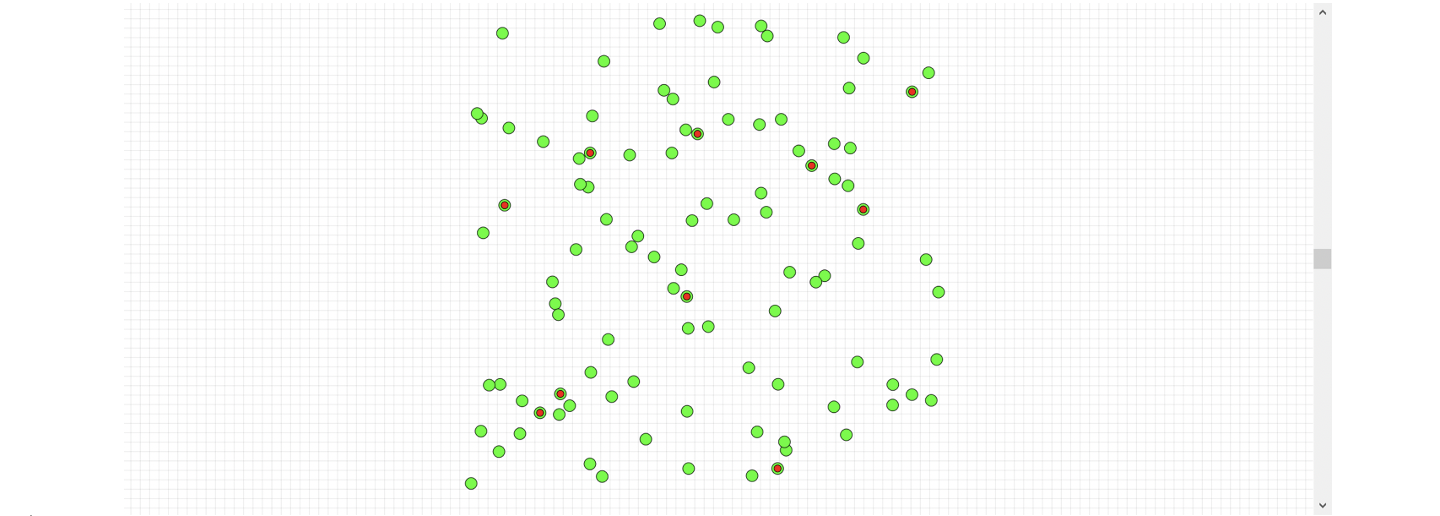
Если запустить модель на расчет, мы получим квадрат, на котором разбросаны в случайном порядке 100 зеленых кружочков. См. рис. 3

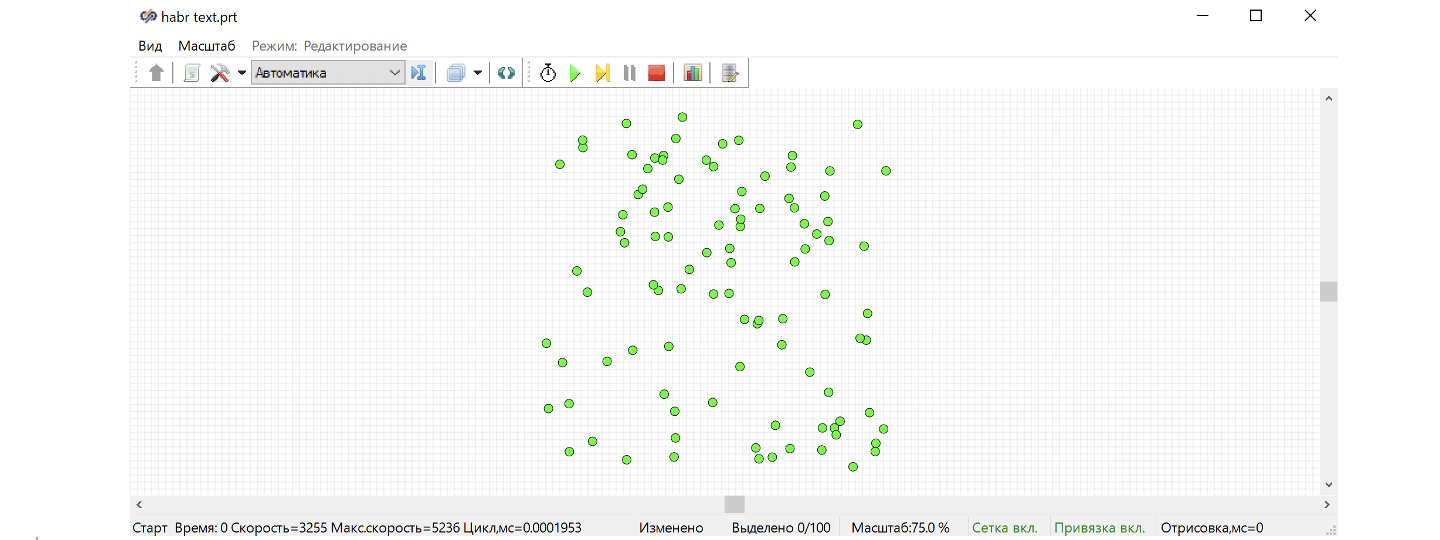
После завершения расчета примитивы на поле не исчезают. Их можно перемещать, изменять и удалять «вручную». Если сделать несколько запусков, то можно убедиться, что при каждом запуске количество городов увеличивается (примитивы создаются), однако в базе данных у нас остается ровно 100 городов, меняются только их координаты. (см. рис.4)

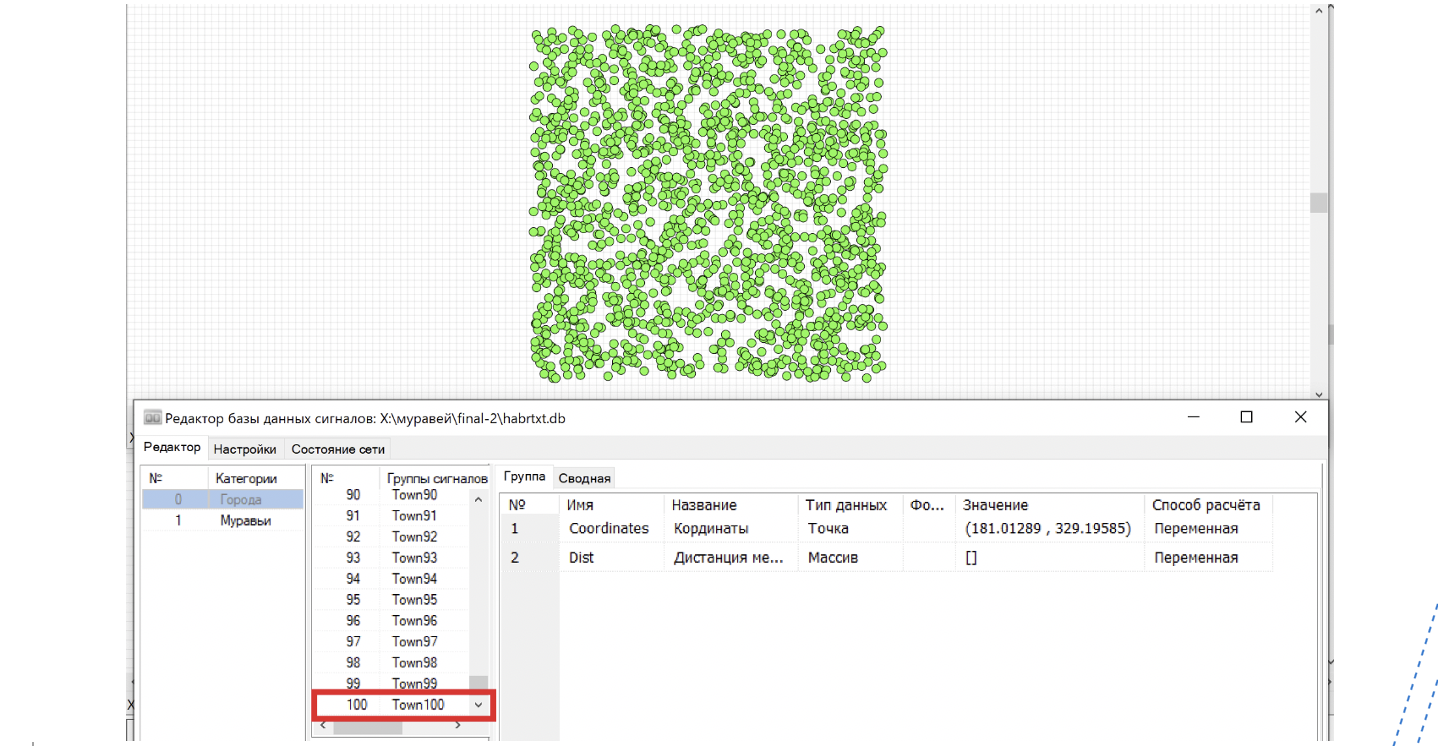
Функция скрипта dbaddgroup("Города",Name,1)  добавляет в базу данных новую группу, только если в базе нет группы с таким же именем. Если объект с таким именем есть, то новая группа не создается. Таким образом, при повторном старте расчета у нас сохраняется количество городов в базе данных, а количество изображений увеличивается.

Чтобы не удалять вручную ненужные изображения, и чтобы при уменьшении заданного количества городов в базе данных не оставались ненужные группы сигналов, давайте вначале уберем все существующие города. 

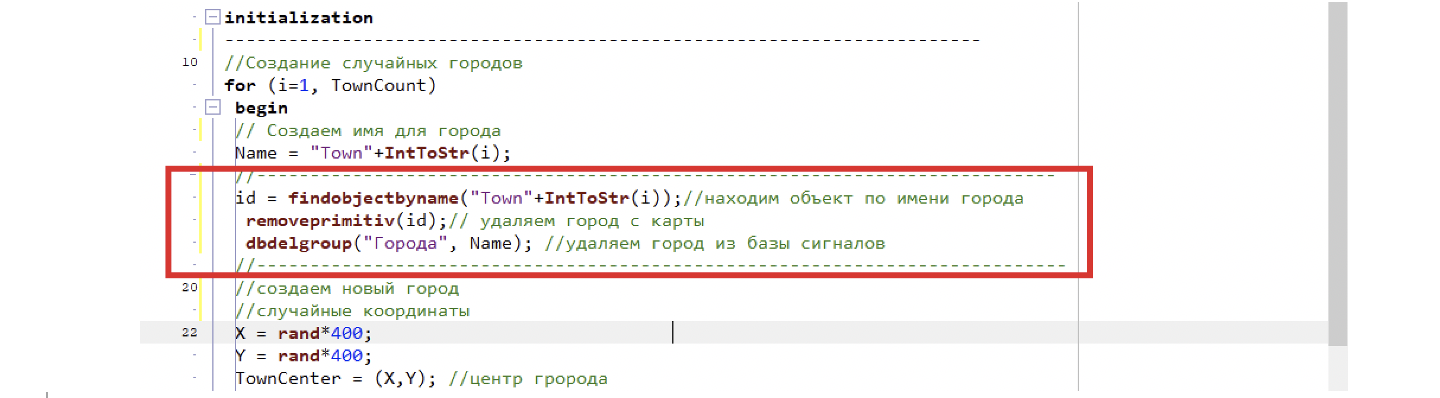
Вычислив имя, прежде чем создавать новые объекты, удали существующие ранее. Для этого вставим три строчки кода для удаления старых данных после создания имени города. Каждый новый расчет – с чистого листа! (см. рис. 5)

Создаем муравьев

Зададим количество муравьев равным 10, добавив в начале еще одну константу.

 AntCount:integer = 10;

Муравьи у нас также будут изображаться кружочками. Можно было бы взять и картинку, но это сделает город более громоздким, а мы все-таки находимся в среде графического программирования, где хочется побольше рисовать и поменьше писать. Поэтому давайте вынесем две строчки кода для создания кружка, обозначающего объект в отдельную функцию см. рис. 6

Муравьи на старте должны быть случайным образом распределены по городам, поэтому нам нужно обратиться к базе данных сигналов и получить координаты случайно выбранного города. 

Для обращения к любой переменной любого проекта служит функция:

getprojectdataptr(projid,"Name"). Она возвращает указатель на переменную в проекте с идентификатором projid и именем Name. 

Другими словами, мы можем достучаться до любого открытого и запущенного проекта и взять любую существующую переменную, в том числе, конечно, переменную, которую мы положили в базу данных сигналов. 

Имя любой переменной в базе данных сигналов у нас состоит из двух частей: имени группы (имя объекта) и имени сигнала. Например: Town1_Coordinates – группа сигналов Town1, переменная Coordinates.

А поскольку мы только что разработали систему кодирования, то нам ничего не стоит сформировать кодирование имени для любого города и любого его параметра.

В итоге код для разбрасывания муравьев по городам и создания изображения муравья на схеме будет выглядеть как на рисунке 7.

Сначала мы получаем идентификатор текующего проекта, функция - getcurrentprojectid;

Затем в цикле для каждого муравья создаем ему имя. Потом случайным образом выбираем номер города, в который мы посадим данного муравья. Для города j, кодированное имя будет "Town"+IntToStr(j), добавляем имя переменной "_Coordinates"   и получим имя переменной для нужных нам координат. 

Функция getprojectdataptr(projid,"Town"+IntToStr(j)+"_Coordinates") вернет нам указатель, далее значение координат присваивается переменной TownCenter.

Зная координаты, мы рисуем в нужном городе кружок с радиусом 3, присваиваем ему имя и меняем его цвет на красный. 

Таким образом, после инициализации схема проекта должна выглядеть, как показано на рисунке 8. 100 зеленых точек – городов. И 10 красных точек – муравьев. 

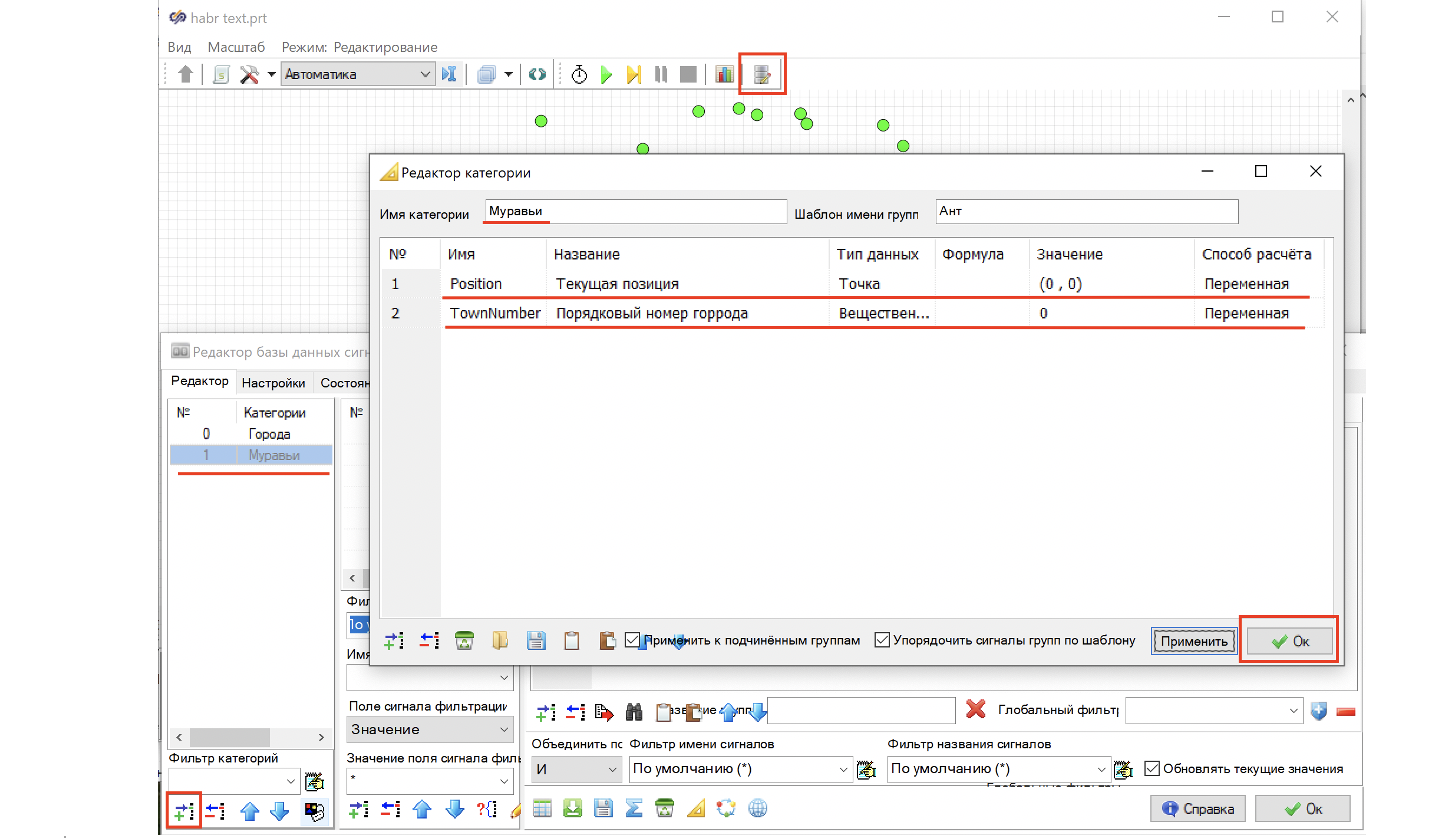
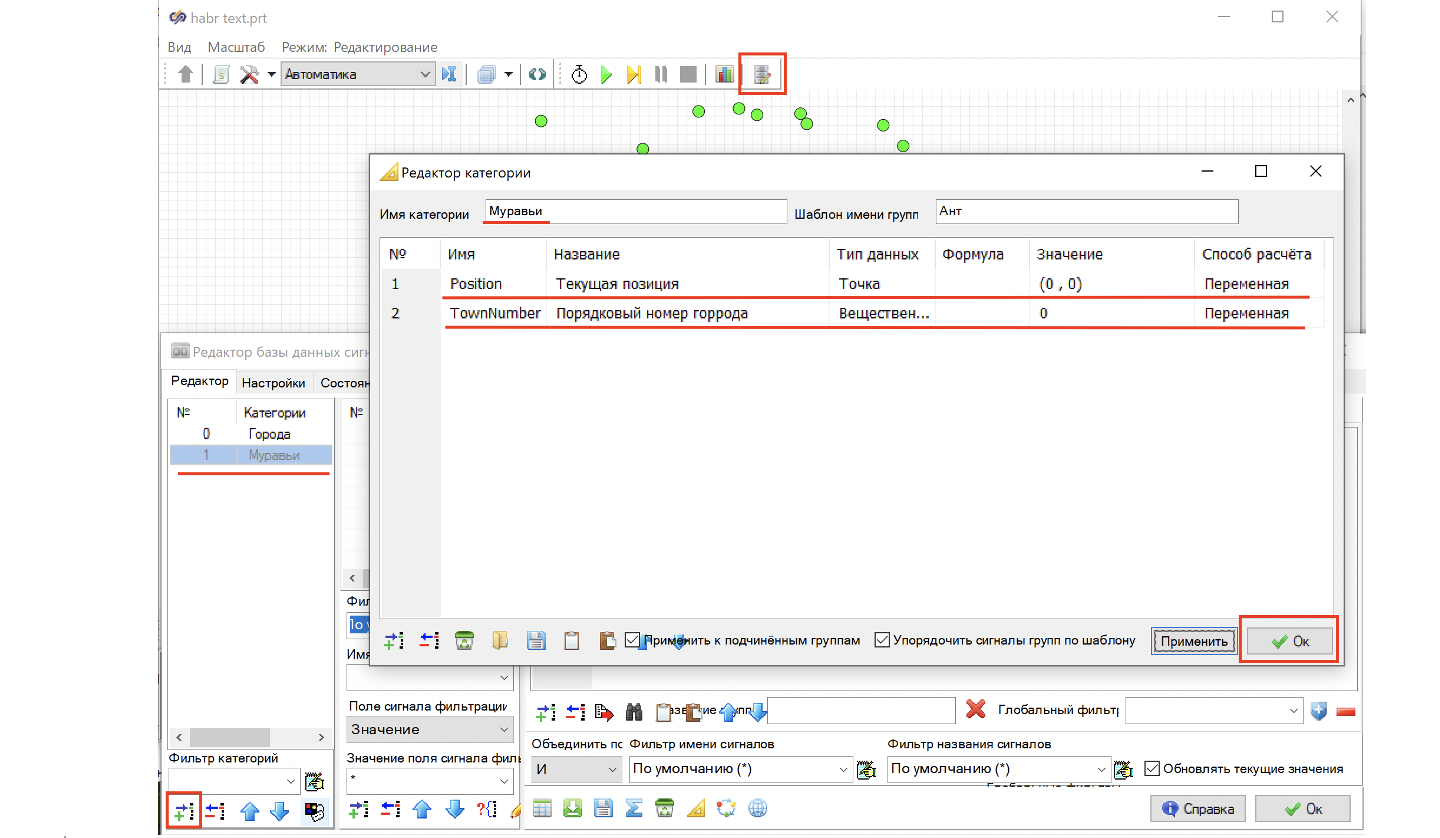
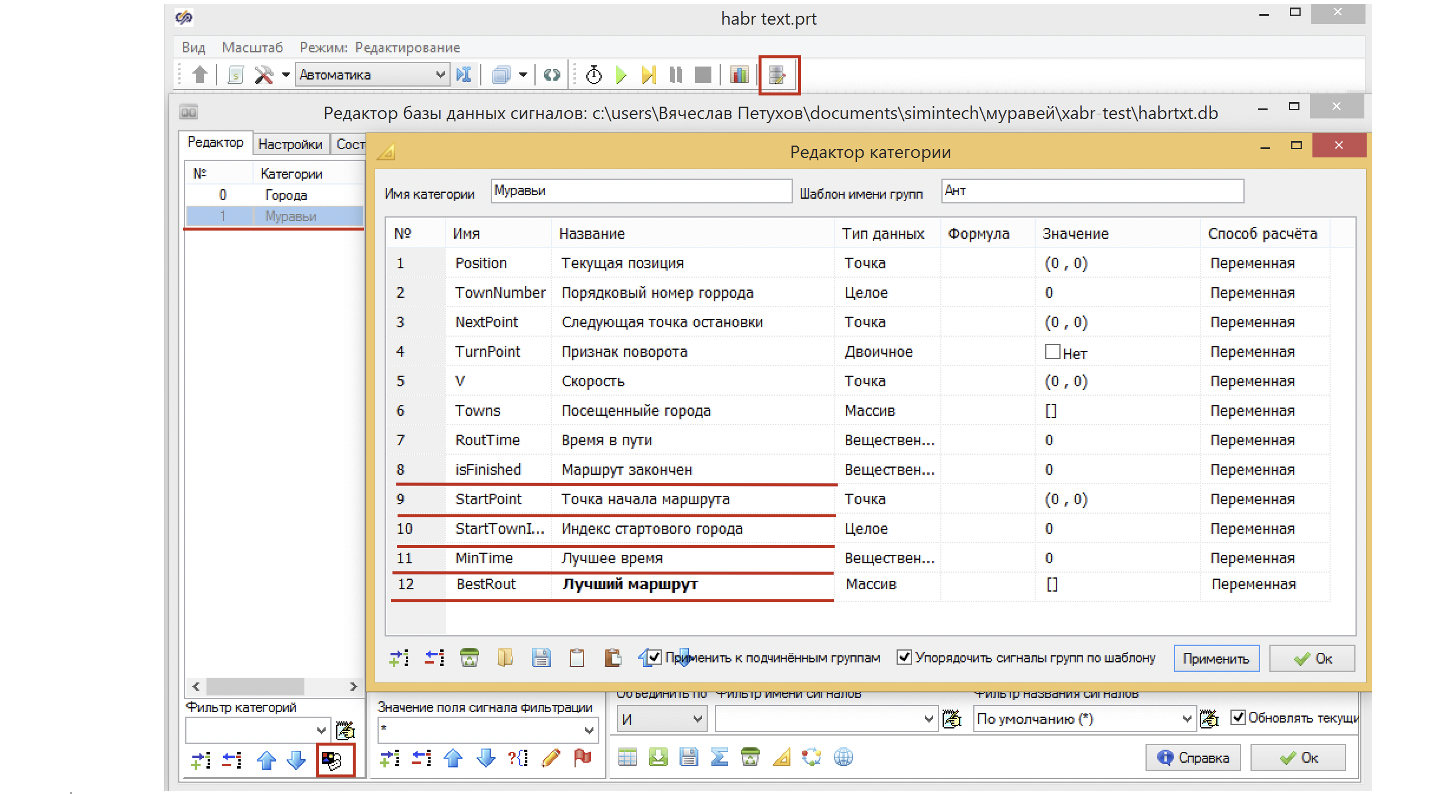
Убедившись, что муравьи у нас распределились по городам, давайте создадим для них категорию в базе данных, где будет храниться вся нужная нам информация по каждому муравью. Для начала добавим категорию «Муравьи», далее в редакторе категории добавляем пока два очевидных поля сигнала Position – Текущая позиция, и TownNumber – Порядковый номер города. (см. рис. 9).

Как только мы подготовили категории (классы) для муравьев, можно добавить в инициализацию код, который заполнит базу данных для каждого муравья. Далее, скорее всего, придется запускать муравьев множество раз по траекториям, поэтому сделаем отдельную процедуру инициализации муравья в выбранном номере. InitAntInTown(AntN,TownN: integer). Вызовем процедуру после создания изображения. 

Также для более читаемого кода изменим функции получения данных из базы сигналов.  Поскольку у нас будет использоваться только один проект, вынесем его идентификатор projid в  глобальные переменные, вычислим его один на этапе инициализации (старта моделирования) и в дальнейшем будем получать данные используя только имя сигнала в базе данных. GetData(C_Name: string);

Добавляем в цикл создания муравья такой же код для удаления старого изображения и старых данных из базы данных.

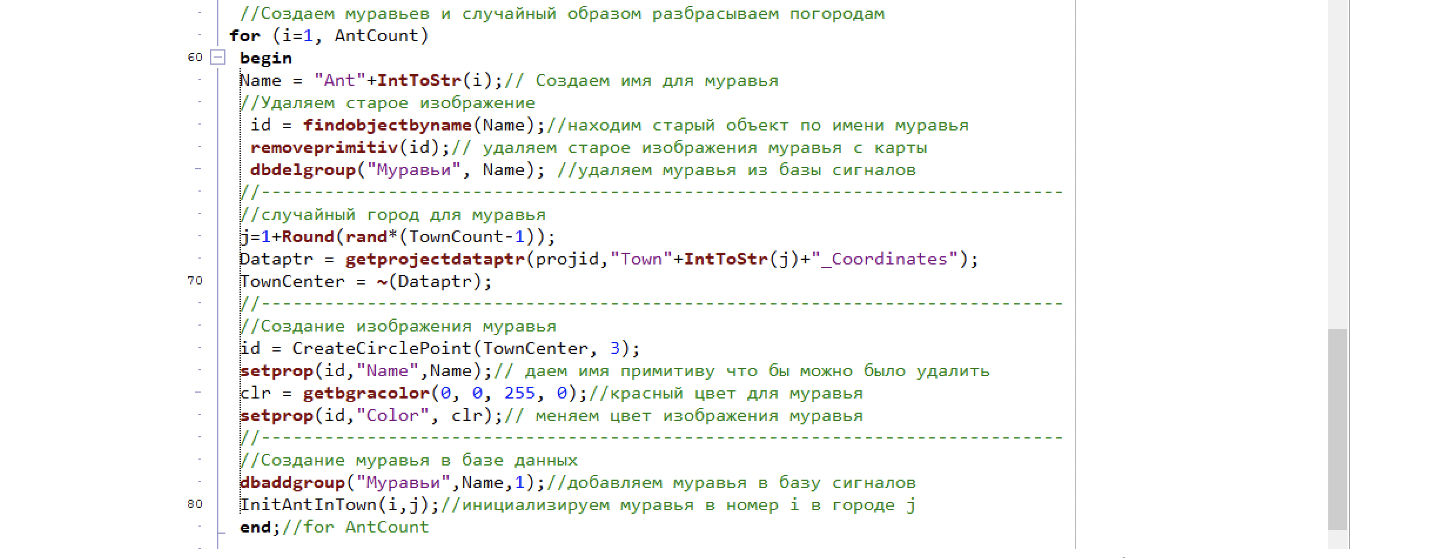
Теперь после создания инициализации проекта в базе данных будет отображаться позиция муравья и номер города, в котором он находится. Можно выделить на схеме красный кружок и убедиться, что его координаты корректно записаны в базе данных под соответствующим именем. См. рис. 12.

Заставим муравья бежать

Прошу прощения у читателей, мне и самому уже надоело писать код, и хочется перейти к визуальному программированию в виде диаграмм. 

Добавим на схему субмодель, где будет реализована логика поведения муравья-агента. 

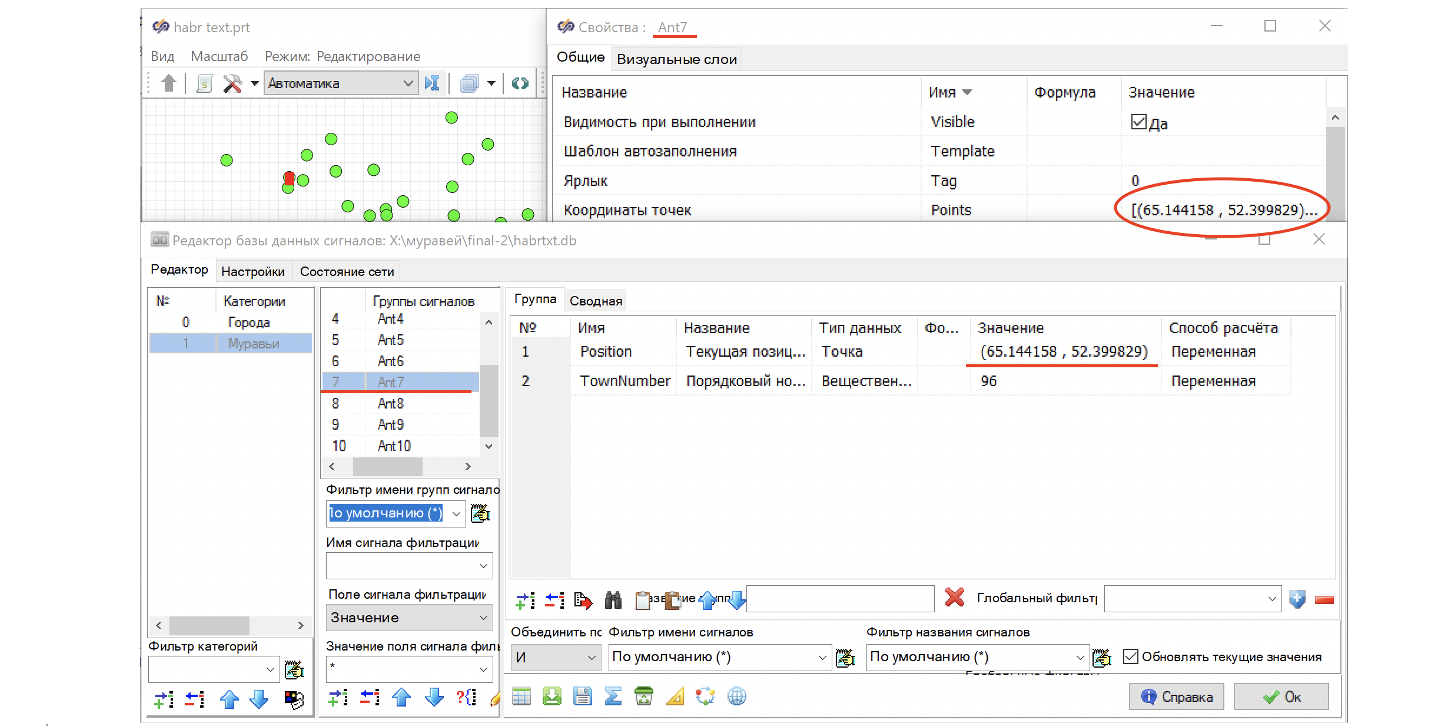
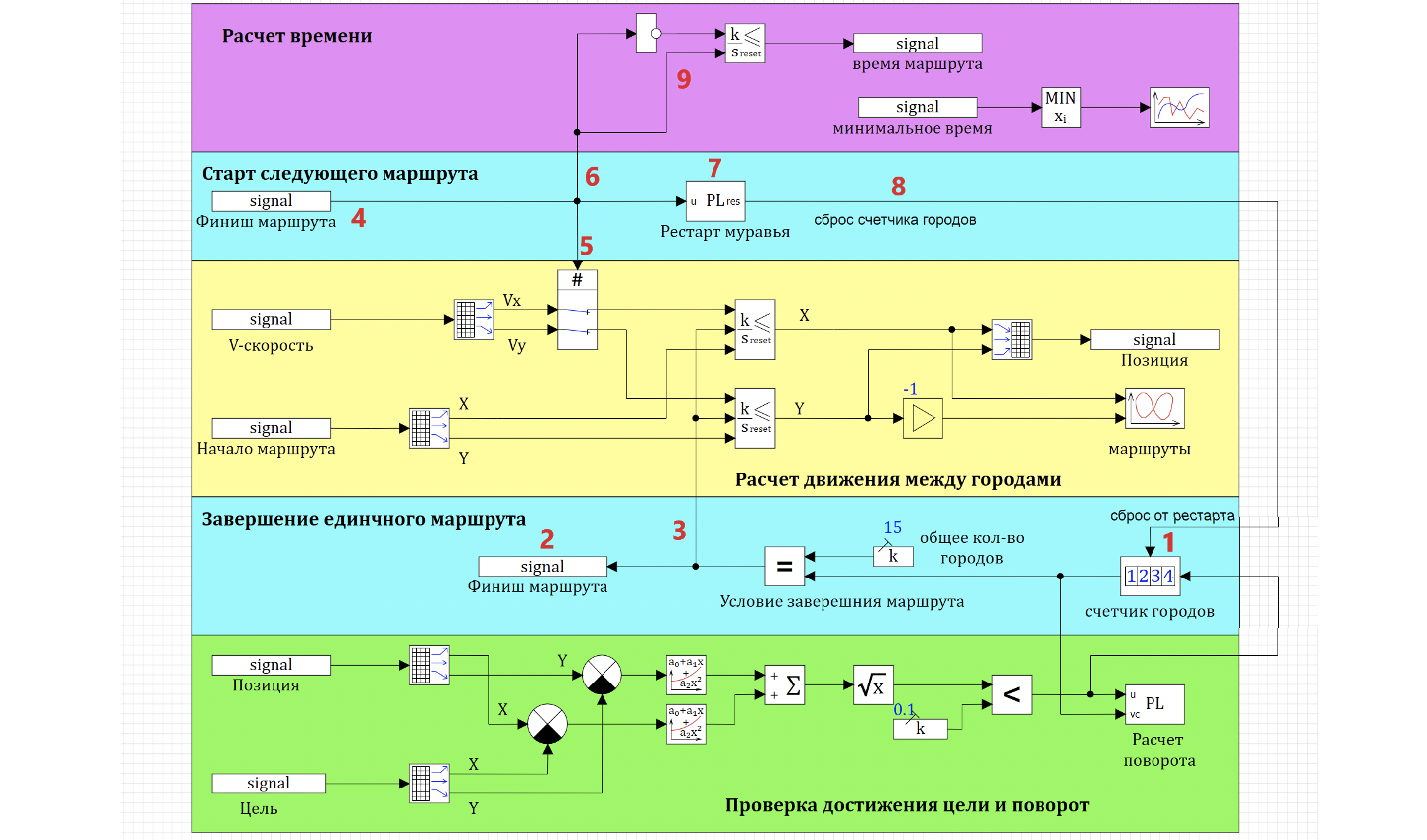
Внутри соберем схему, представленную на рисунке 13. Алгоритм работы, следующий:

Из базы данных сигналов забирается позиция муравья. Поскольку она состоит из двух чисел, координат Х и У, то ее с помощью блока распаковки разбираем на две составляющие Х и Y и используем в качестве начальных условий для интеграторов со сбросом. (В дальнейшем сброс нужен для перезапуска муравья, в этой схеме сброс всегда равен 0.). В интеграл также подается скорость перемещения (в данном случае она равна 1). Во время расчета интегрирующее звено увеличивает позицию согласно заданной скорости. Для контроля перемещения используется фазовый портрет, куда выводятся значения, полученные после интегрирования. Значение Yумножается на -1 для соответствия отображения на графике и графическом поле.

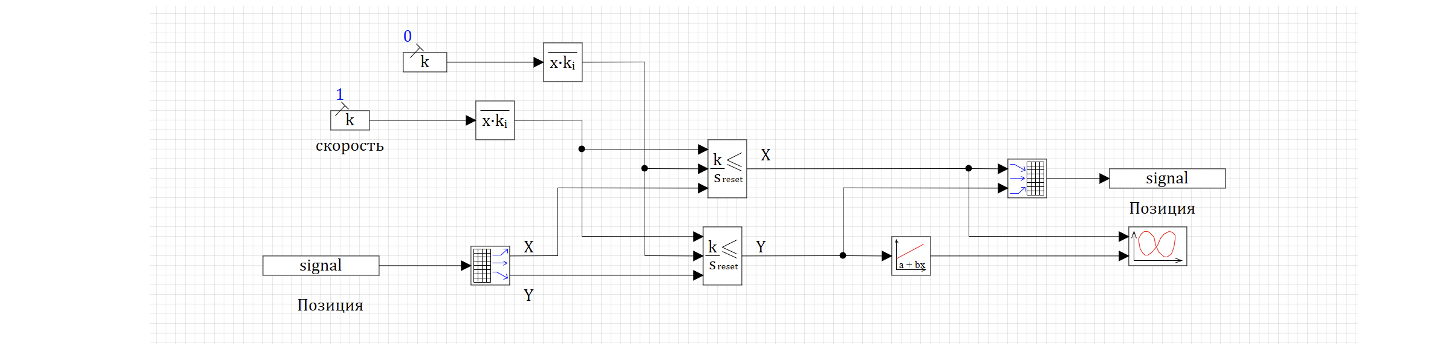
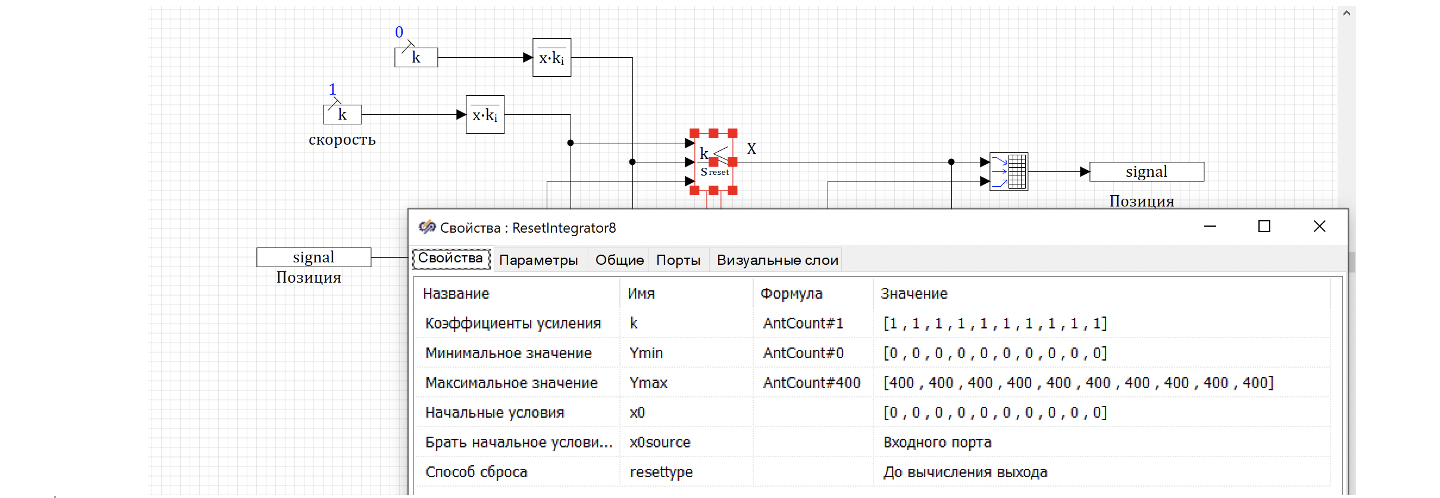
Как мы видим на рисунке 13, схема расчета положения муравья у нас одна. Однако муравьев может быть множество. Каким образом наши блоки знают, сколько муравьев нужно обсчитывать? Все просто. На самом деле количество муравьев определено в глобальных константах главного скрипта (AntCount: integer = 10;), соответственно в настройках блока мы можем использовать эту константу AntCount, чтобы настроить «векторную обработку данных» Например, для интегратора со сбросом настройки выглядит так, как показано на рисунке 14.[AK1] 

Таким образом везде, где нам нужно показать размерность вектора, мы просто используем AntCount, и наша расчетная схема обсчитывает всех муравьев на схеме, которые были заданы при начале расчета.

Например, мы задаем значения максимального положения для всех муравьев равному ширине поля – 400, для этого пишем AntCount#400

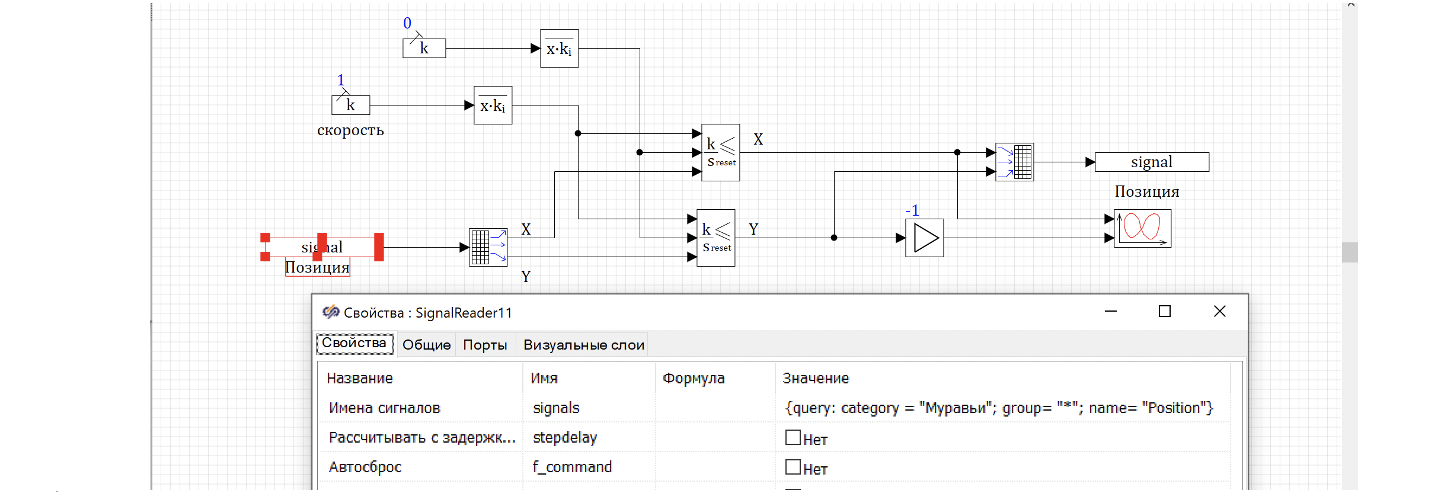
Чтобы забрать все позиции из базы данных, мы используем блок «Чтение из списка сигналов». В блоке мы записываем запрос, забирающий все нужные сигналы из базы данных. В данном случае мы забираем позиции всех муравьев: 

({query: category = "Муравьи"; group= "*"; name= "Position"})

Точно такой же запрос используется для записи посчитанного положения в базу данных.

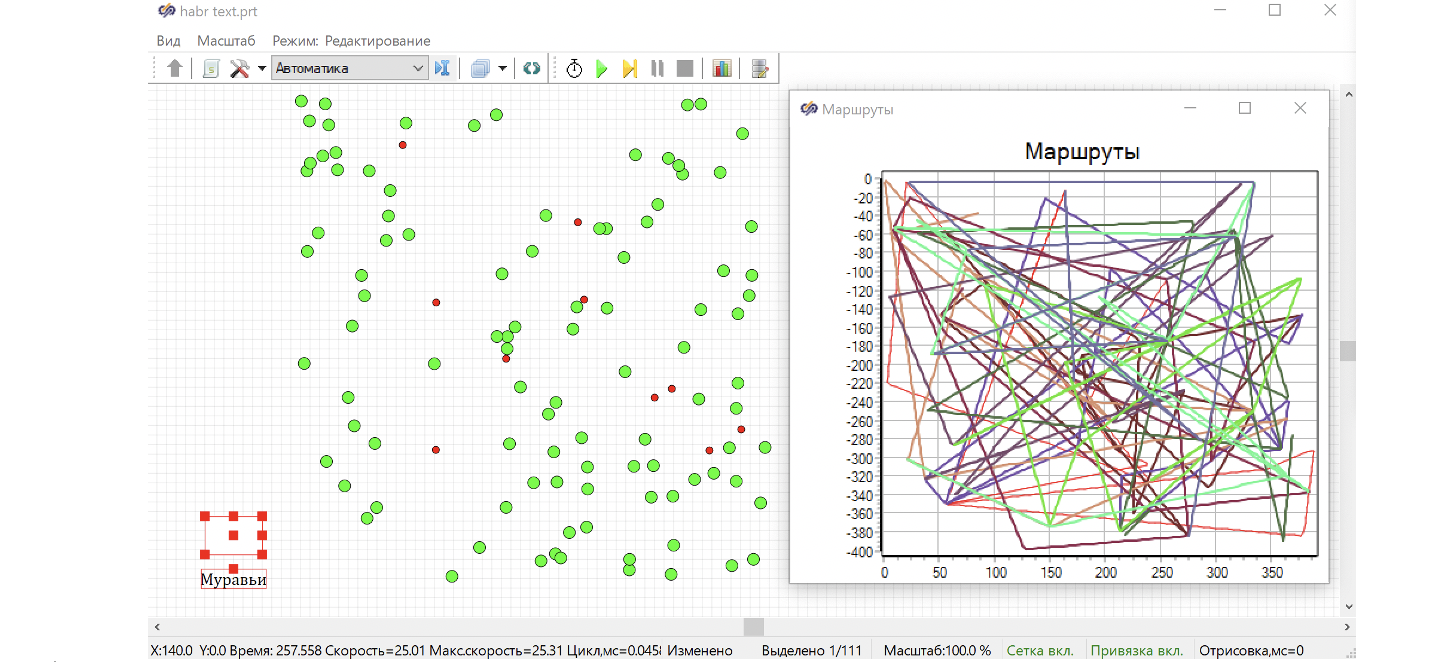
Если запустить на расчет модель, то на графике можно увидеть, что все точки смещаются по Х и У с одинаковой скоростью относительно их положения. Например, если установить время расчета 100 сек., мы получим картину как на рисунке 16.

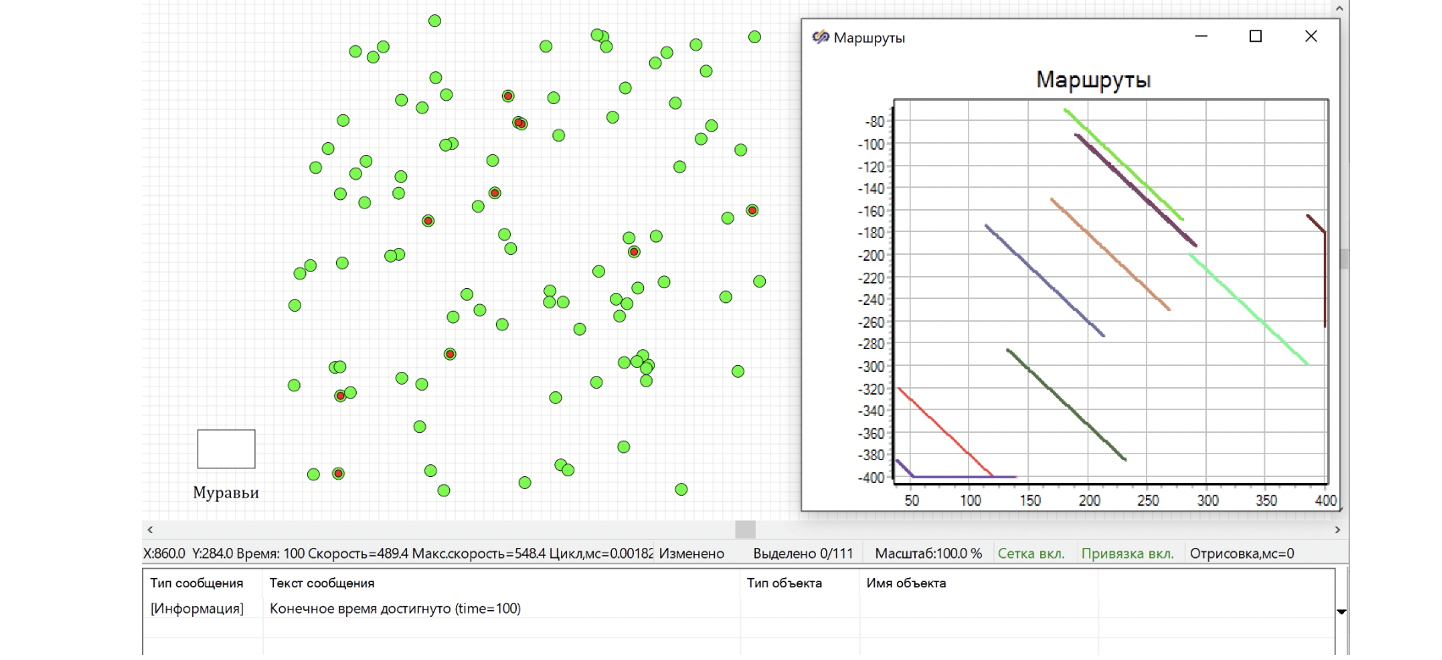
Все муравьи побежали! Видно, что положение маршрутов на графике соответствует начальному положению муравьев на схеме. Перемещение идет с одинаковой скоростью. Если муравей добегает до края поля, то начинает бежать вдоль него. Поскольку интегратор ограничивает перемещение. Например, на рисунке 16 на графике видно, что один из муравьев доходит до ограничителя в интеграторе по оси Х, и в дальнейшем уже перемещается только по оси У. Другой достиг края по оси У.

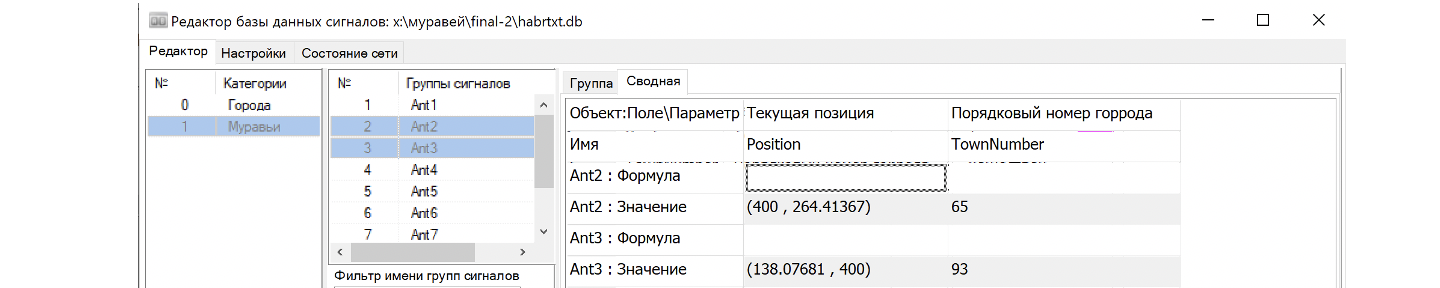
Открыв базу данных, можно убедиться, что, рассчитанные значения для муравьев сохраняются в соответствующих полях базы сигналов. Например, для муравьев, достигших края поля, значение сигнала, позиция соответствуют графику. Один из них добрался до края по Х, а другой до края по Y (см. рис. 16 - 17)

Бег на графике — это конечно хорошо, но еще лучше, чтобы бегали и на схеме. Для этого возвращаемся в скрипт, и добавляем код, который перемещает красные кружочки муравьев согласно рассчитанной позиции. Вернемся в главный скрипт и добавим следующий код после секции инициализации:

В этом коде все достаточно просто: проходим циклом по всем муравьям, забираем положение из базы данных, затем находим объект с именем муравья и меняем его свойства, сохраняя позицию, чтобы он не прыгал обратно по завершению расчета.

Пусть муравьи бегут, куда надо, а куда не надо, не бегут

Получив схему агента, которая заставляет муравья куда-то бежать, давайте теперь научим агента бежать в нужную сторону. От горда к городу. В нашей модели мы приняли, что исходными данными для расчета положения муравья, скорость по Х и У, с точки зрения типа данных это точка, с двумя координатами. Добавим в базу данных муравья его скорость в качестве сигнала V.

Чтобы рассчитать направление движения, необходимо знать координаты места цели. Чтобы агент-муравей бежал куда надо, он должен знать координаты этого самого «куда надо». По условию задачи муравей должен обежать все города, то есть в процесс моделирования, точка «куда надо», будет меняться.

Изменение направления будет происходить в момент, когда муравей добежит до очередного города. А значит координаты города, в который бежит муравей, должны быть в базе данных. Также, как и признак поворота. Добавим поля в базу данных и в процесс инициализации муравья.

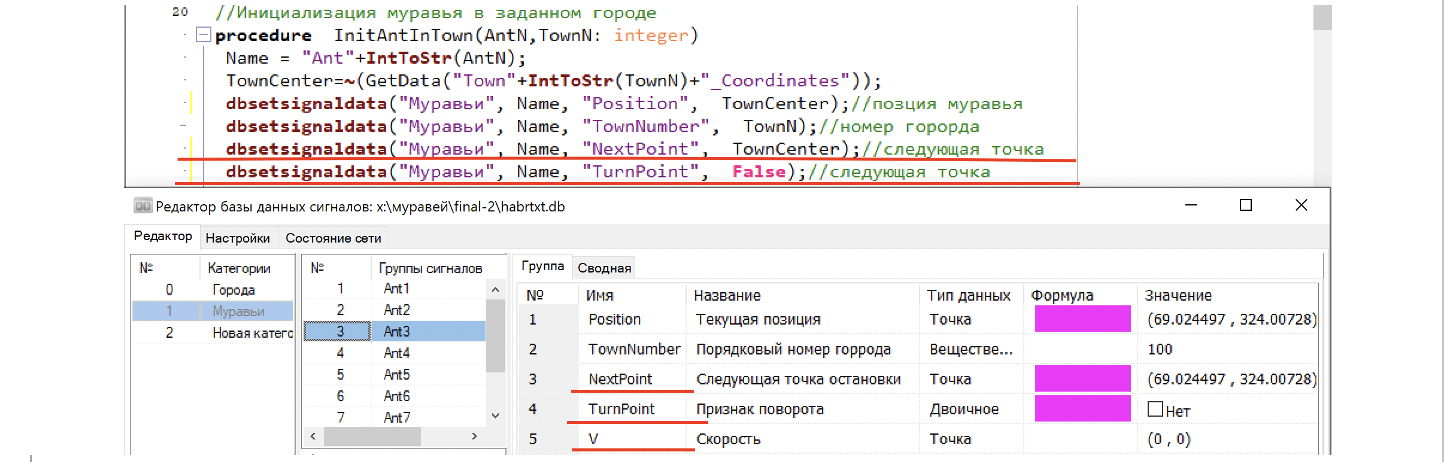
В начальный момент времени у нас муравей уже находится в той точке, где ему нужно принимать решение о повороте. Создадим схему расчета достижения точки принятия решения о выборе следующего города! Определить точку поворота очень легко, если у нас расстояние между текущей позицией и целевой меньше заданной величины, например 0.1, значит муравей достиг города и нужно менять его направление.

Формула расчета простая и знакома каждому муравью:

Зная текущие координаты и координаты цели, высчитывается дельта и расстояние. 

Схема такого расчета приведена на рисунке 20:

Запрограммируем теперь прохождение поворота муравья в блоке «Язык программирования».  Логика работы достаточно простая: вектор проверки достижения цели передается в качестве входа, далее в языке программирования, для каждого муравья проверяется достижение цели, если да, то тогда находим для него новый город для посещения (пока случайным образом) и рассчитываем направления и задаем скорость.  (см. рис. 21):

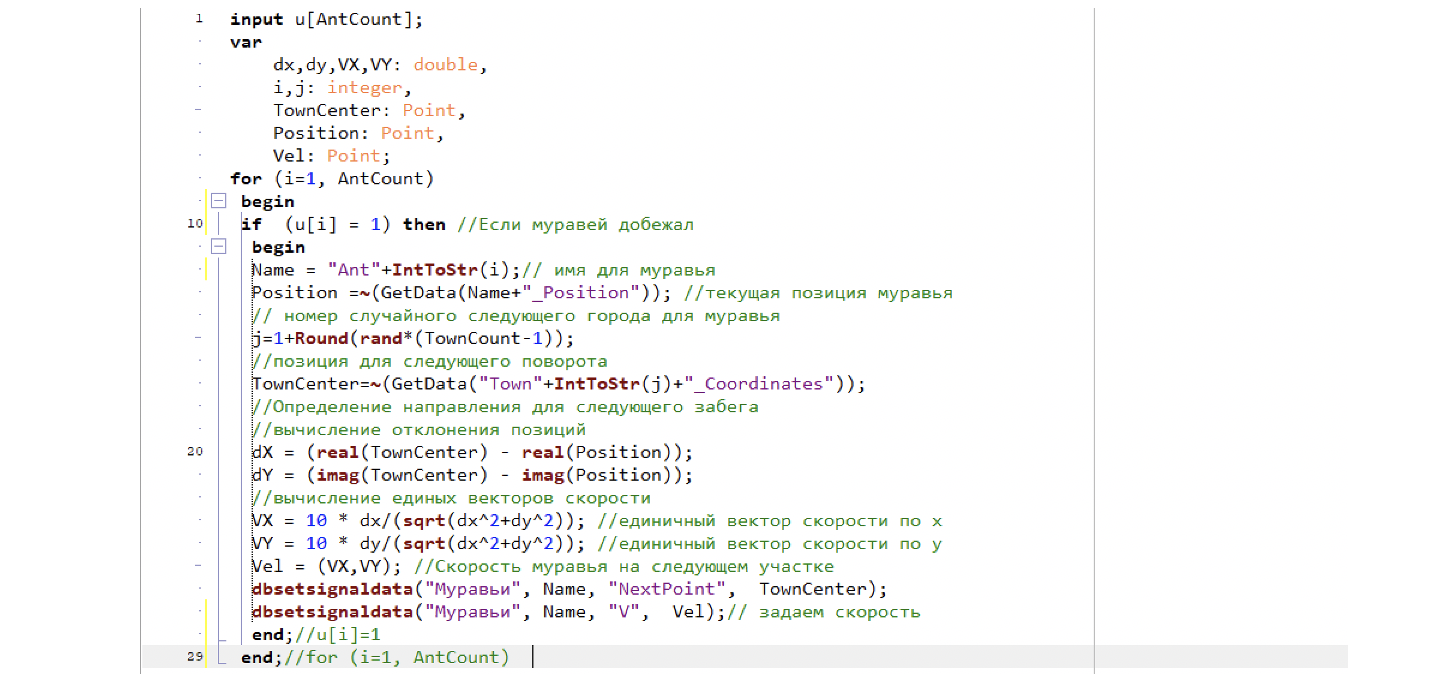
В принципе скрипт понятный, единственно требует пояснения вот эта запись:

dX = (real(TownCenter) - real(Position));

dН = (imag(TownCenter) - imag(Position));

 Делов в том, что тип Точка, в точности соответствует типу комплексного числа, где есть действительная часть – X, и мнимая часть – Y. Чтобы получить действительную и мнимые части, мы используем функции работы с комплексными числами, таким образом получаем Х и Y.

После присвоения новой целевой точки и расчета направления бега, мы записываем скорость в базу данных сигналов, а потом на схеме считываем ее. Таким образом наши муравьи бегут не абы куда, а каждый в свой следующий город. 

Для этого вместо константы скорости (рис. 13) мы используем блок «чтение из списка сигналов», в котором в используем запрос, возвращающий скорости всех муравьев. ( {query: category = "Муравьи"; group= "*"; name= "V"})

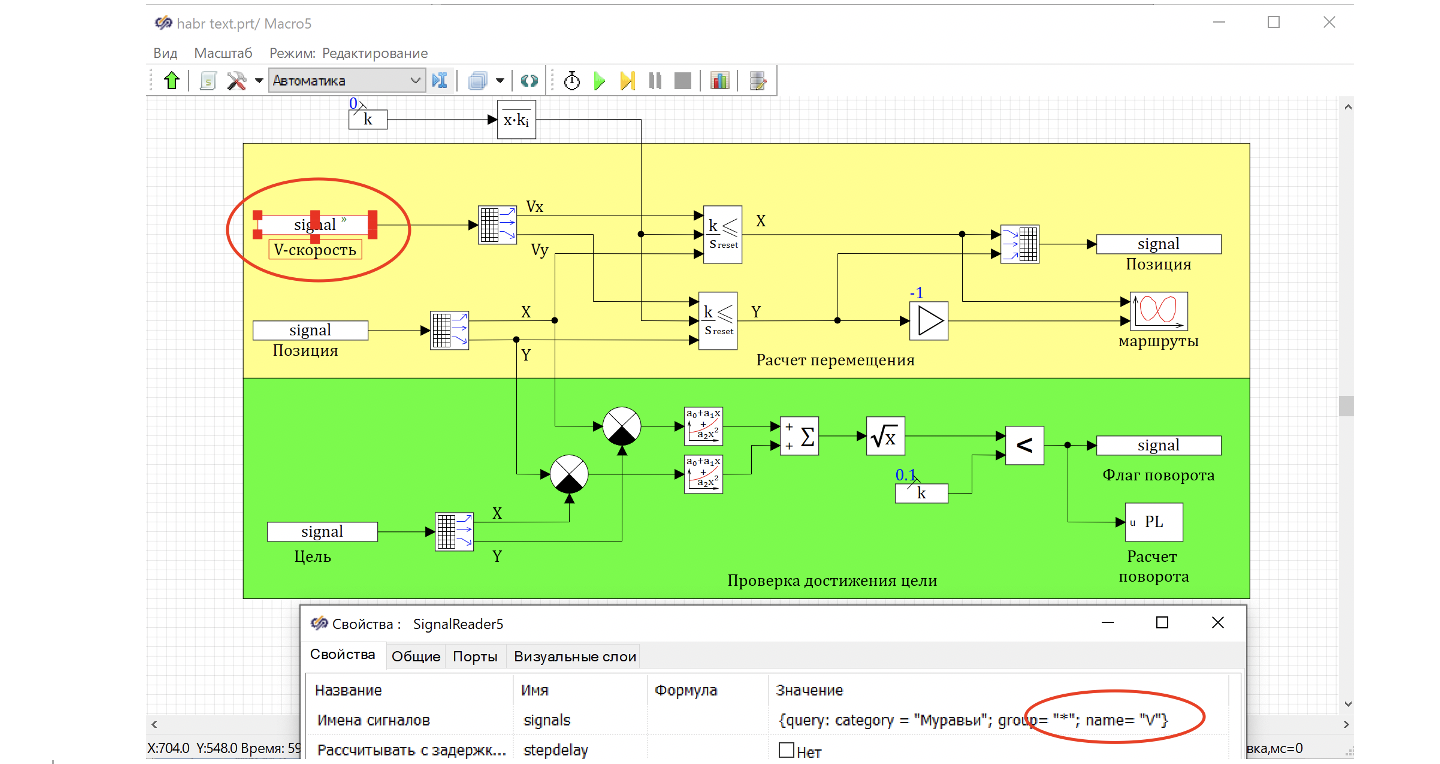
Если сейчас запустить на расчет можно увидеть, как красные муравьи наводят суету, а фазовый портрет отображает их хаотическое перемещение по городам.

Остановитесь!

Давайте теперь выполним расчёт посещенных городов и остановку, когда все муравьи побывали в 100 городах. Пока у нас движение случайное, они могут побывать и в одном городе несколько раз, но мы забьём пока на это несоответствие исходным данным и сделаем учет количества поворотов.

Для этого на схему поставим блок «Счетчик» (1. Рис. 24). Данный блок будет фиксировать количество прохождений муравья через точку поворота. Чтобы не рисовать линию через всю схему, воспользуемся блоками «В память» (2. Рис. 24 ), «Из памяти» (3. Рис. 24).

Полученное значение счетчика сравним с количеством городов (4. Рис. 24), и когда количество посещённых городов, сравняется с количеством всех городов, мы обнулим скорость. Для этого результат сравнения отправим на блок «Ключ управляемый нормально замкнутый» (5. Рис. 24 ). Пока сигнала управления нет, этот ключ передает значение скорости на интегратор. Как только приходит сигнал управления, ключ размыкается, на интегратор поступает 0 и муравей останавливается.

Добавим также остановку расчета, когда все муравьи обойдут по 100 городов.

Для этого просто просуммируем вектор остановки движения (6. Рис. 24) и сравним с количеством муравьев (7. Рис. 24), если они равны, значит все муравьи остановились и можно останавливать расчет (8. Рис. 24).

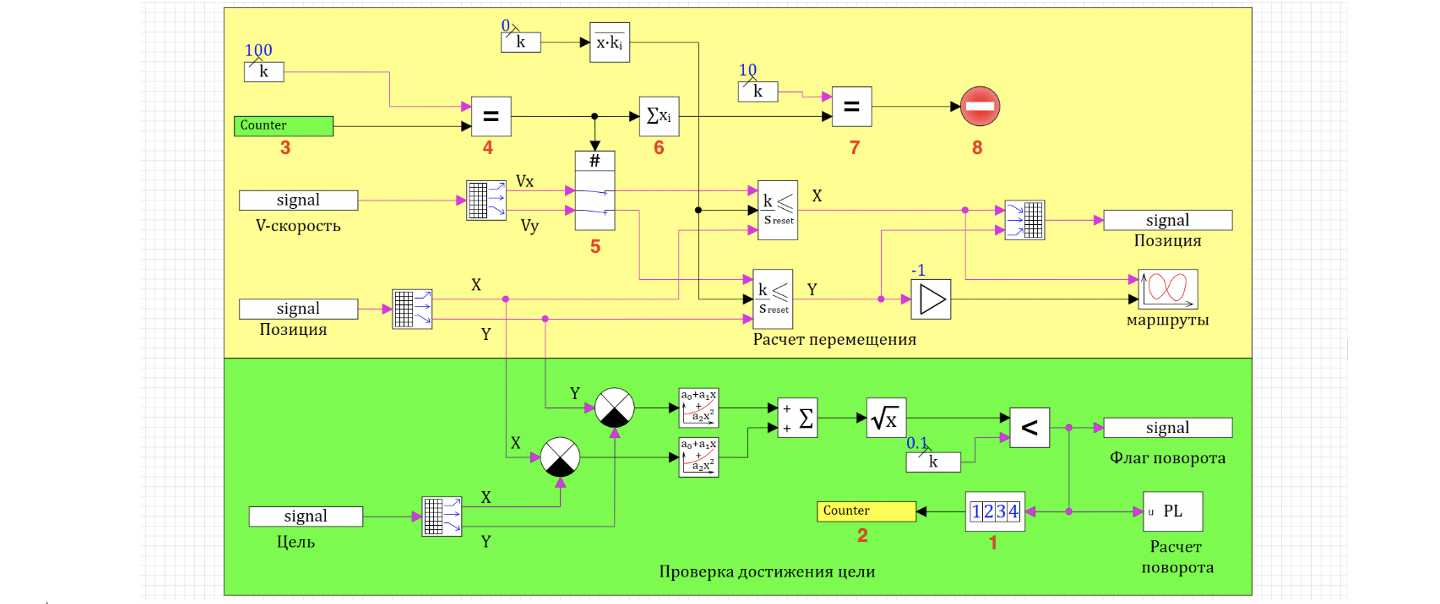
Если теперь установить время расчета, равное 2000 секундам, и запустить моделирование, то можно убедиться, что часть муравьев успела пройти через сотню городов, а часть нет. 

Если вывести значение на линии связи после счетчика, то видно, что у четырех муравьев счетчик городов показывает 100. А у 6 муравьев – меньше. Видно, что как раз 4 муравья уже добежали до города и остановились, поскольку скорость на интегратор не передается, а 6 муравьев продолжали движение, и в конце расчета оказались между городами.

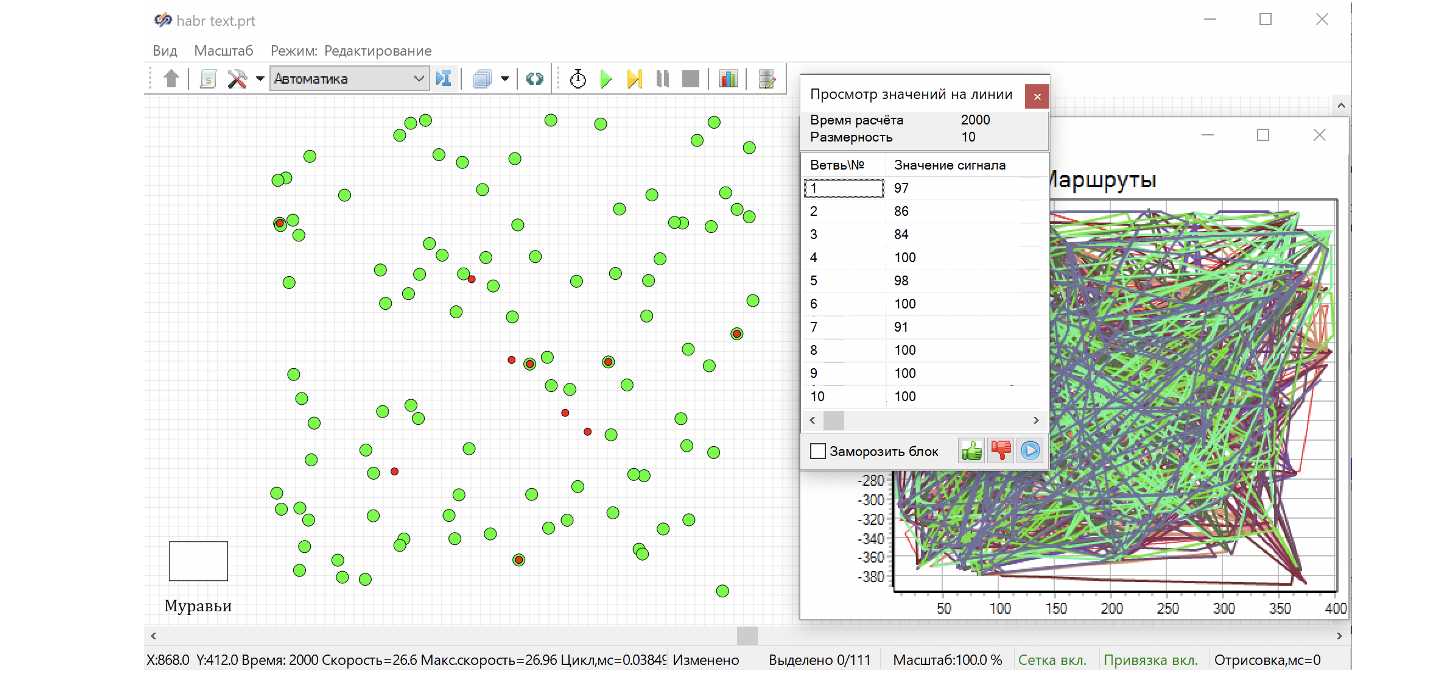
Мы еще раз убедились, что модель агентов, созданная в виде одной функциональной схемы, работает и позволяет рассчитывать независимое поведение для всех муравьев!

Ordnung, ordnung  uber alles!

Наши агенты муравьи уже отлично бегают между городами, и даже останавливаются, когда 100 раз повернут, но это еще хаотическое движение, поскольку каждый раз мы случайно выбираем следующий город, а это непорядок! 

Более того, иногда при случайном выборе номера города, выбранный город оказывается тем самым, где муравей уже находится, и мы получаем ошибку деления на ноль при расчете скорости. 

А значит, муравью необходимо запоминать в каком городе он уже побывал, и выбирать нужно из тех городов, которых он еще не посещал. Это значит у муравья должна быть память! Добавим в структуру данных агента-муравья новый сигнал Towns -  Посещенные города,  типа Массив. 

А в процедуру инициализации города - создание нулевого массива. (cм. Рис. 26)

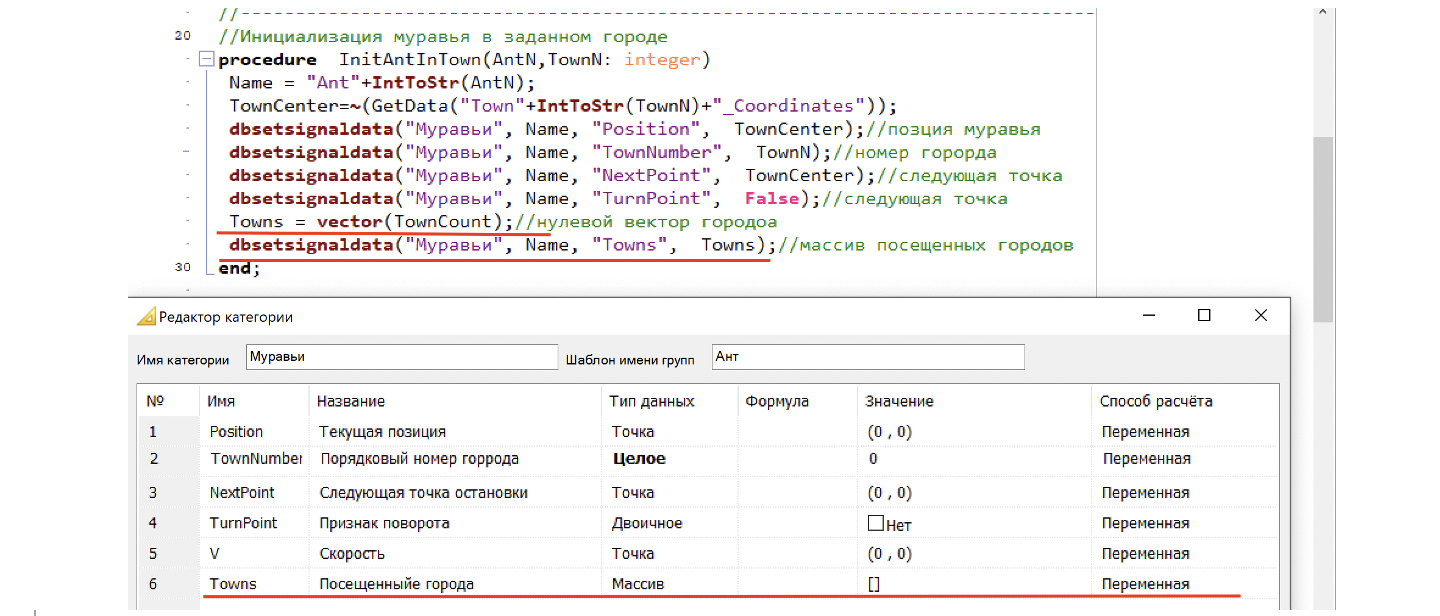
Теперь, когда у нас муравей помнит, какие города он посетил, мы можем выбирать следующий город. Изменим схему, добавив счетчик поворотов в качестве входа в блок «Расчета поворота». (см. рис. 27).

После этого изменения на вход в блок «Расчет поворота» передается признак поворота и порядковый номер этого поворота для муравья.

Каждый муравей знает индекс (TownNumber) города, куда он бежал до поворота, мы в массиве для этого города записываем номер поворота, полученный со счетчика поворотов (VC[i]). А потом передаем этот массив для расчета следующего города в функции SelectTownIndex(Towns); (см. рис. 28)

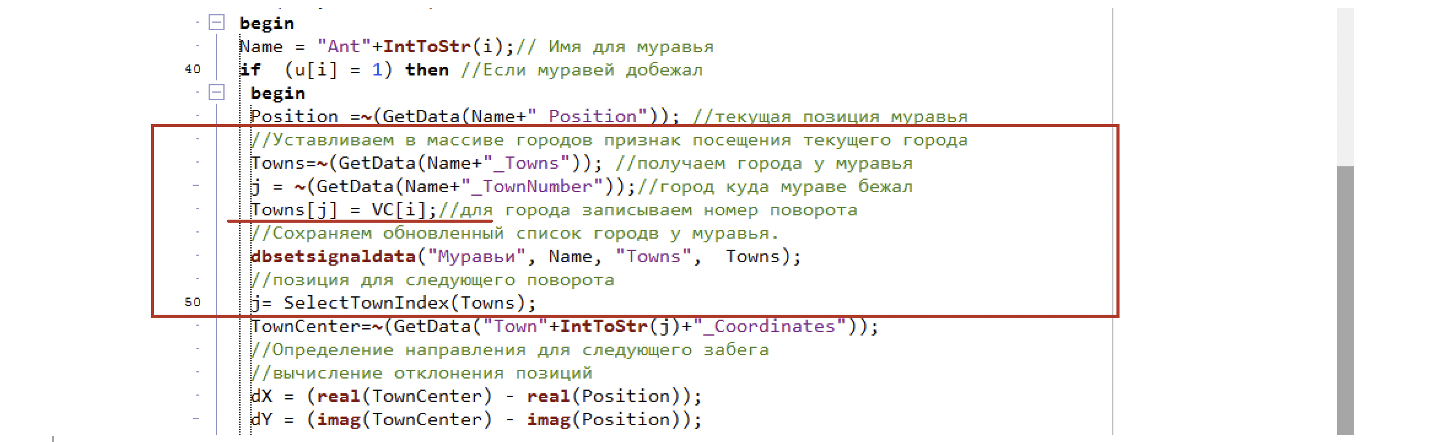
Выбор следующего города для поворота осуществляется следующим образом: мы задаем максимальную вероятность выбора maxprob=0 и выбранный selectedIndex =1. Далее в цикле мы генерируем случайное число от 0 до 1 для каждого города. Если город уже посещен (в массиве ему соответствует номер поворота заведомо больше 0), то мы сбрасываем сгенерированную вероятность до 0. Далее эта вероятность сравнивается с максимальной: если она больше, то индекс города становится выбранным индексом. Если нет, индекс остается, и мы переходим к следующему городу.

Таким образом, на выходе мы получим индекс города, для которого случайное число оказалось самым большим. Текст процедуры представлен на рисунке 29.

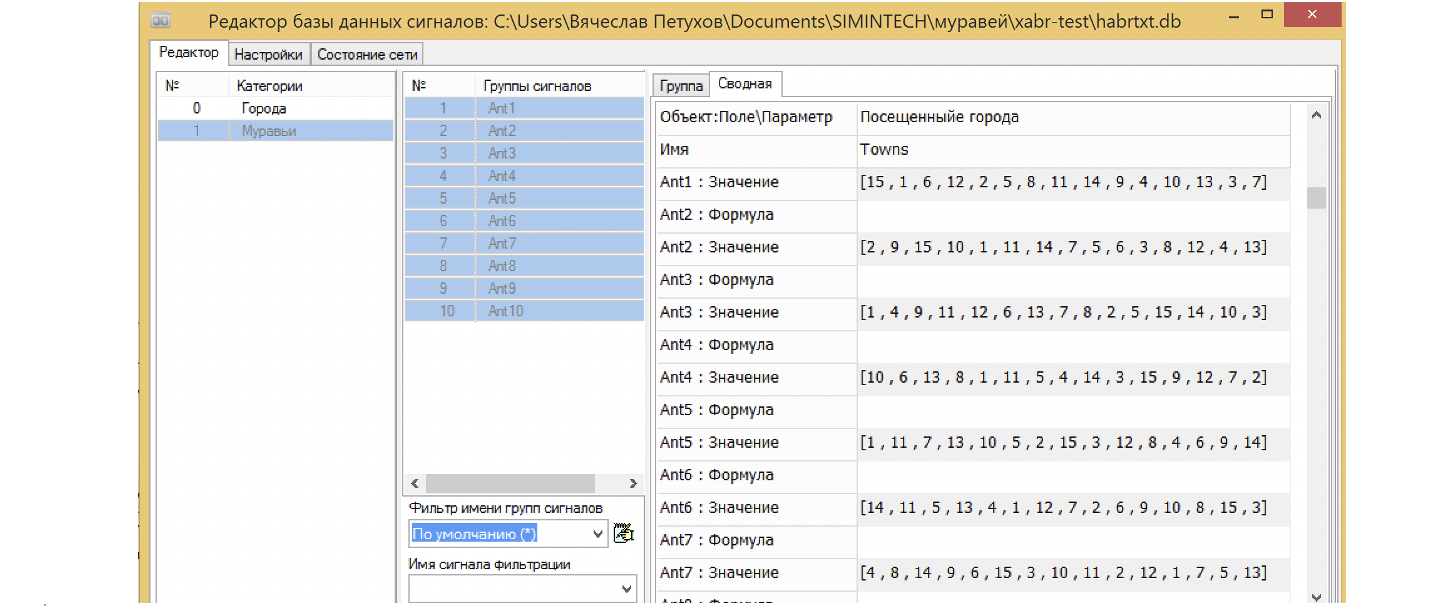
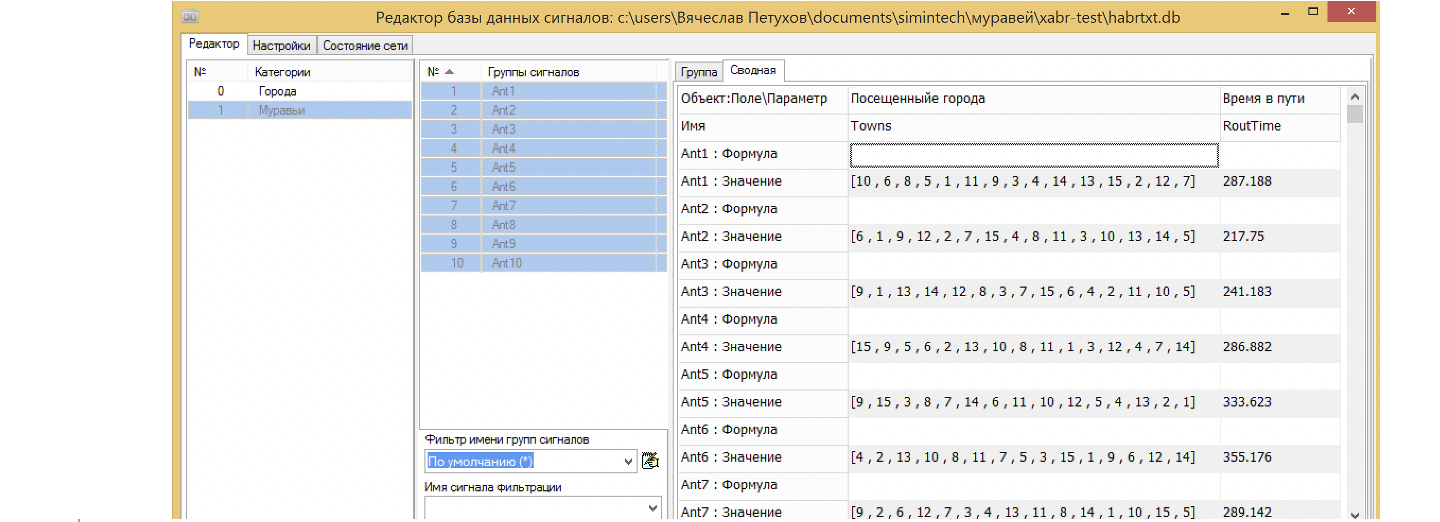
Теперь можно в базе данных наблюдать, как муравей пробегает по городам, заполняя массив городов номерами поворотов, сохраняя маршрут в своей памяти агента. Вид базы данных для 15 городов и 10 муравьев представлен на рисунке 30.

Время - деньги!

Мы так долго организовывали броуновское движение муравьев, что совсем забыли зачем они тут суетятся. А они хотят найти самый короткий путь. Казалось бы, интегратор и есть блок, который рассчитывает расстояние по скорости, но не в нашем случае. У нас интегратор считает положение, поэтому на выходе у нас болтанка, как на рисунке 25. 

Поэтому мы будем считать деньги, то есть время. Скорость у нас задается постоянной, поэтому достаточно посчитать время, пока муравей бежал, чтобы определить длину пути. Для этого достаточно подключить интегратор к линии остановки бега. Пока муравей бежит, в линии у нас 0, мы интегрируем с коэффициентом 1, как только счетчик поворотов совпал с количеством городов в линии, интегрирование можно останавливать, на выходе интегратора останется время забега. Остается только сохранить его в базе данных сигналов для каждого муравья под именем «RoutTime». Схема расчет проста, как 3 копейки (cм. рис. 31).

Теперь если запустить десять муравьев по 15 городам, мы по завершению расчета получим в базе данных для каждого агента муравья маршрут и время в пути. (см. рис. 32)

Повторение – мать учения

После того как наши агенты муравьи стали настолько умными, что уже не путаются в городах, они могут рассчитать время движения, составить и даже запомнить маршрут движения, (блин, я уже волнуюсь за Скайнет), давайте еще увеличим им интеллект. 

Давайте еще немного усложним им задачу. Пусть они запоминают свой город старта и по завершении маршрута бегут его с начала. Повторяют обход городов до тех пор, пока не кончится время моделирования процессов. Этот же процесс можно описать, как смерть агента-муравья в конце маршрута, и одновременное рождение нового в начале с тем же именем. Как только одно поколение муравьев пробежало маршрут, мы запускаем следующее из точки старта.

Выбор каждого последующего города у нас случайный, и каждый новый забег будет давать новый маршрут.  Мы добавим лучшее время забегов в память агента (сигнал в базе данных), и, если новый маршрут окажется быстрее запомненного, агент обновит это время.  Таким образом, мы получим множество прохождений маршрута, размер которого ограничен только временем расчёта. Больше считаем – больше вариантов пробега.

Добавим новые поля в базу данных:

StartPoint  –  точка начала маршрута

StartTownIndex – индекс первого города маршрута;

MinTime – лучшее время;

BestRout – лучший маршрут.

В новом варианте моделирования остановка расчета после прохождения маршрута всеми муравьями не происходит, а значит, нам нужно для каждого муравья учитывать момент завершения забега, поэтому добавляем в базу данных сигнал isFinished – флаг завершения расчета.

Изменения в алгоритме расчета поворота у нас минимальные, для счетчика добавляем сброс (1. Рис 34), который происходит после рестарта муравья. После обхода всех городов, мы записываем в базу данных флаг окончания расчета в сигнал isFinished  (2. Рис. 34), и отправляем сигнал на сброс интеграторов в модели движения ( 3. Рис. 34).

Начало следующего маршрута происходит после чтения сигнала isFinished (4. Рис. 34). Этот сигнал разрывает связи скорости с блоком интегрирования в расчете движения между городами (5. Рис. 34), останавливает интегратор времени (6 Рис. 34,) и предаётся в блок рестарта муравья (7. Рис 34), где выполняется сброс текущего маршрута и запуск нового. Запуск нового забега вызывает сброс счетчика (8. Рис. 34).

Для расчета времени мы добавили сброс интегратора. Когда стартует следующий маршрут, происходит сброс интегратора (9. Рис. 34), и время маршрута начинает рассчитываться заново. Минимальное время по всем муравьям выводится блоком чтения сигналов в виде вектора, затем минимальное из всех выводится на график, что позволяет отслеживать, как находят самый быстрый маршрут.

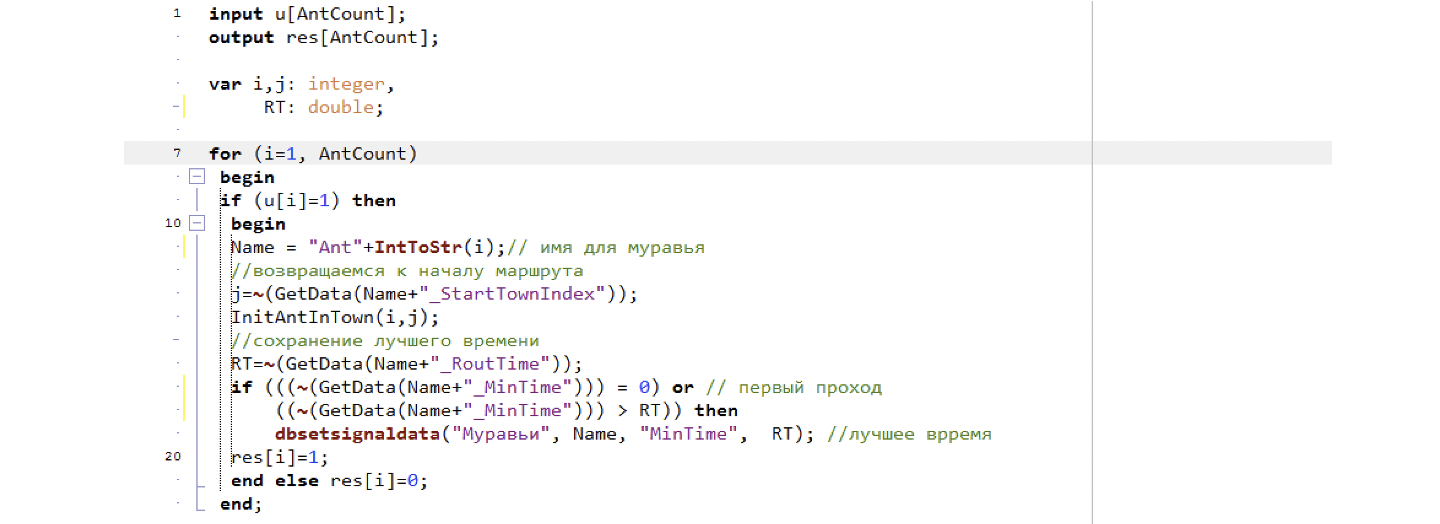
Код рестарта муравья у нас простой, если не сказать примитивный. Получив вектор завершения расчета, проходим по всем муравьям, если вектор равен 1, что значит True, отправляем муравья на стартовую позицию, сохраняем лучшее время забега (не забывая проверить, не первый ли это пробег, когда лучшее время равно 0), и отправляем команду на сброс счетчика городов. (см. рис. 35).

Теперь, если запустить модель на расчет, муравьи бегают, каждый раз меняя маршрут случайным образом, обходят все города и запоминают лучшее время прохождения. Созданная модель ищет лучший путь путем перебора.

В качестве примера: установим время моделирования 5000. 15 городов и 10 муравьев, у меня получилось лучшее время – 194 сек. При среднем времени прохождения в 300 секунд. Десять муравьев за 5000 секунд модельного времени пробежали всего около 160 – 200 вариантов маршрута.

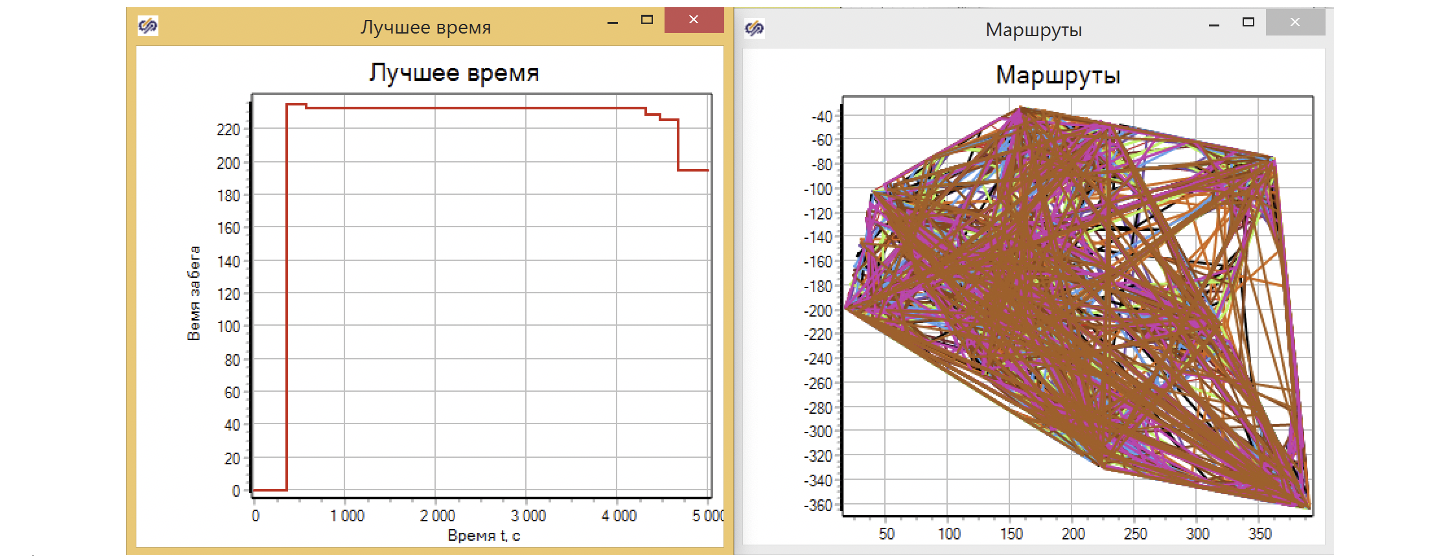
Увеличим в 10 раз количество муравьев, пускай на маршрутах их будет 100. Оставим те же самые города для чистоты эксперимента. Для простоты в скрипте закомментируем код для удаления и создания городов на этапе инициализации. В этом случае все объекты «города» в базе данных и на схеме, сохранятся с предыдущего расчета. 

Запустим 100 муравьев и посмотрим, какой лучший маршрут они найдут. На рисунках  37 –  результат запуска сотни муравьев на маршруты между 15 городами. Видно, что плотность покрытия маршрутами возросла, время улучшилось.

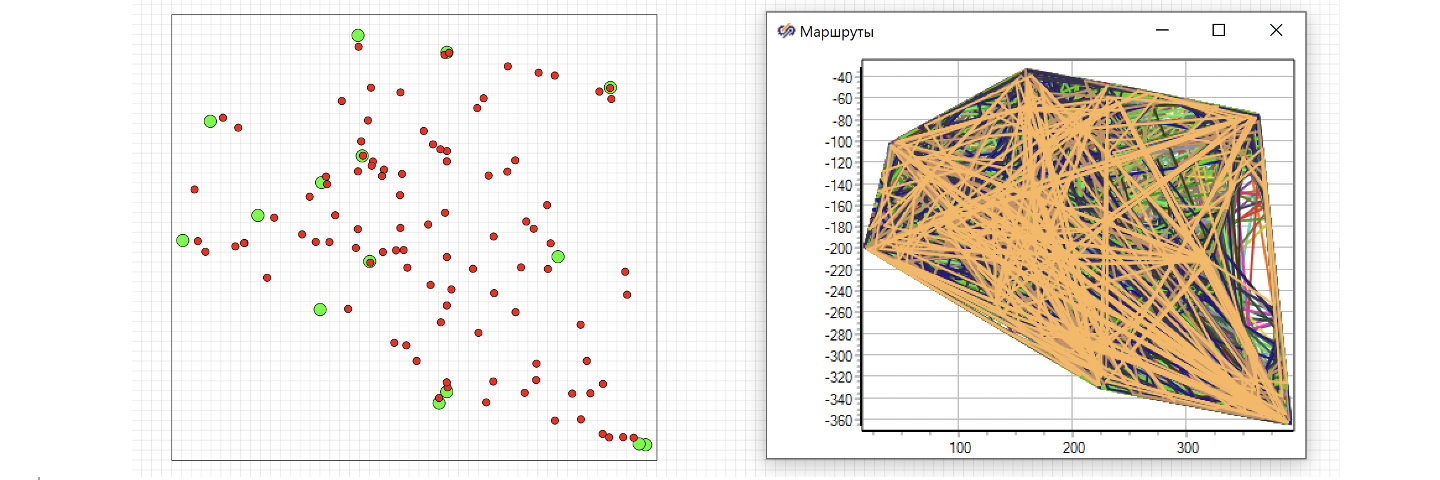
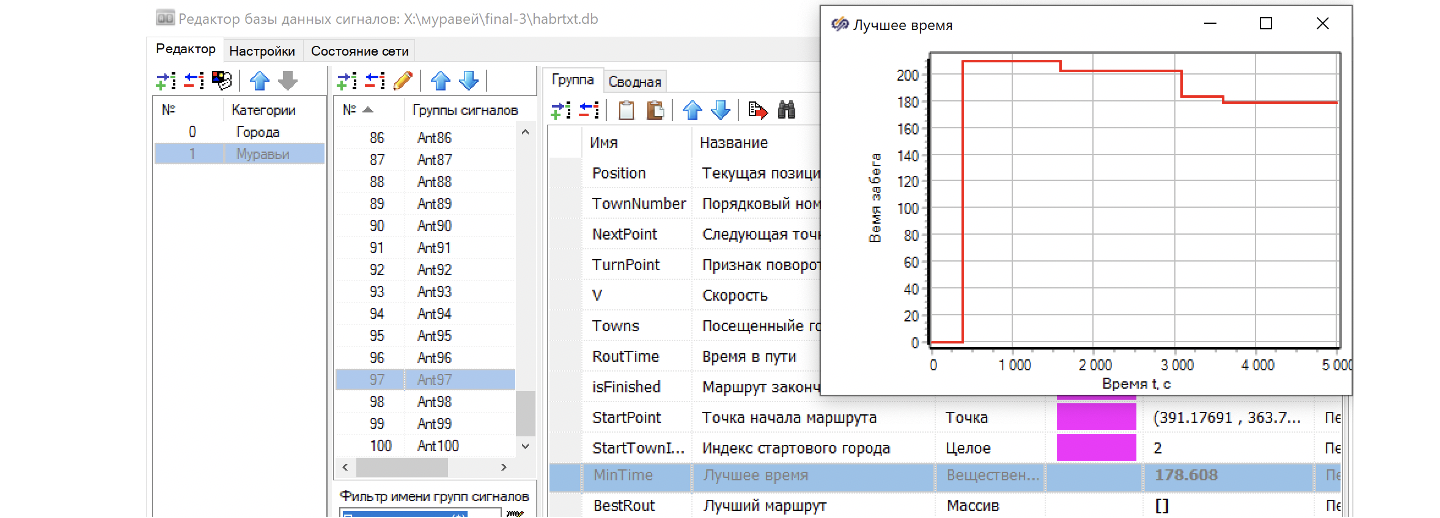
Победителем соревнований стал муравей под номером 97, его рекорд составил 178.608 секунд. См. рис.  38

Улицы ждут отпечатков наших ног

После того, как мы научили муравье бегать хаотично, но упорядоченно[AK1] , можно переходить непосредственно к «Муравьином алгоритму». Потому что до этого мы постоянно повышали интеллект нашего муравья, снабжая его памятью, логикой выбора маршрута и умением перезапускаться. Пора добавить ему инстинктов и научить оставлять следы «на пыльных дорожках далеких планет». 

Суть муравьиного алгоритма заключается в том, что выбор в точке поворота происходит неслучайно. Настоящий муравей при движении оставляет след из феромонов. Следующий за ним муравей может почувствовать это след и повторить маршрут предшественника. Но при этом сами феромоны имеют свойство испаряться. Чем длиннее маршрут, тем больше времени нужно для его завершения и тем больше испарится феромонов.  Таким образом, происходит естественная настройка маршрутов на самый короткий, феромона на котором будет больше всего.

Чтобы сохранить феромоны на тропе, мы добавим каждому городу массив, который будет содержать количество феромона, оставляемого муравьем при выборе направления. Чем чаще муравьи будут выбирать в точке поворота конкретный город, тем больше феромона будет в элементе соответствующего массива, и следующий муравей будет использовать эти данные для выбора очередного города.

Добавим в категорию города массив феромонов. См. рис. 39

При инициализации проекта заполним его нулевыми значениям. (см. рис. 40) 

Теперь, когда в городах есть место, где муравей может оставить следы феромонов, изменим процедуру выбора города для поворота. Теперь в процедуре будет учитываться не только массив посещенных в забеге городов, но также и выбор, сделанный другими муравьям в этом городе.

Для этого мы находим по индексу город, получаем массив феромонов, которые соответствуют переходу из данного города в другие города. (1. Рис. 41). Кроме случайного выбора, добавляем в вероятность количество феромонов соответствующего выбора (2. Рис. 41). Получив индекс города с максимальной вероятностью перехода, добавляем в массив феромонов для этого города. (3. Рис. 43).

Теперь для другого муравья шансы выбрать этот же маршрут повышаются. 

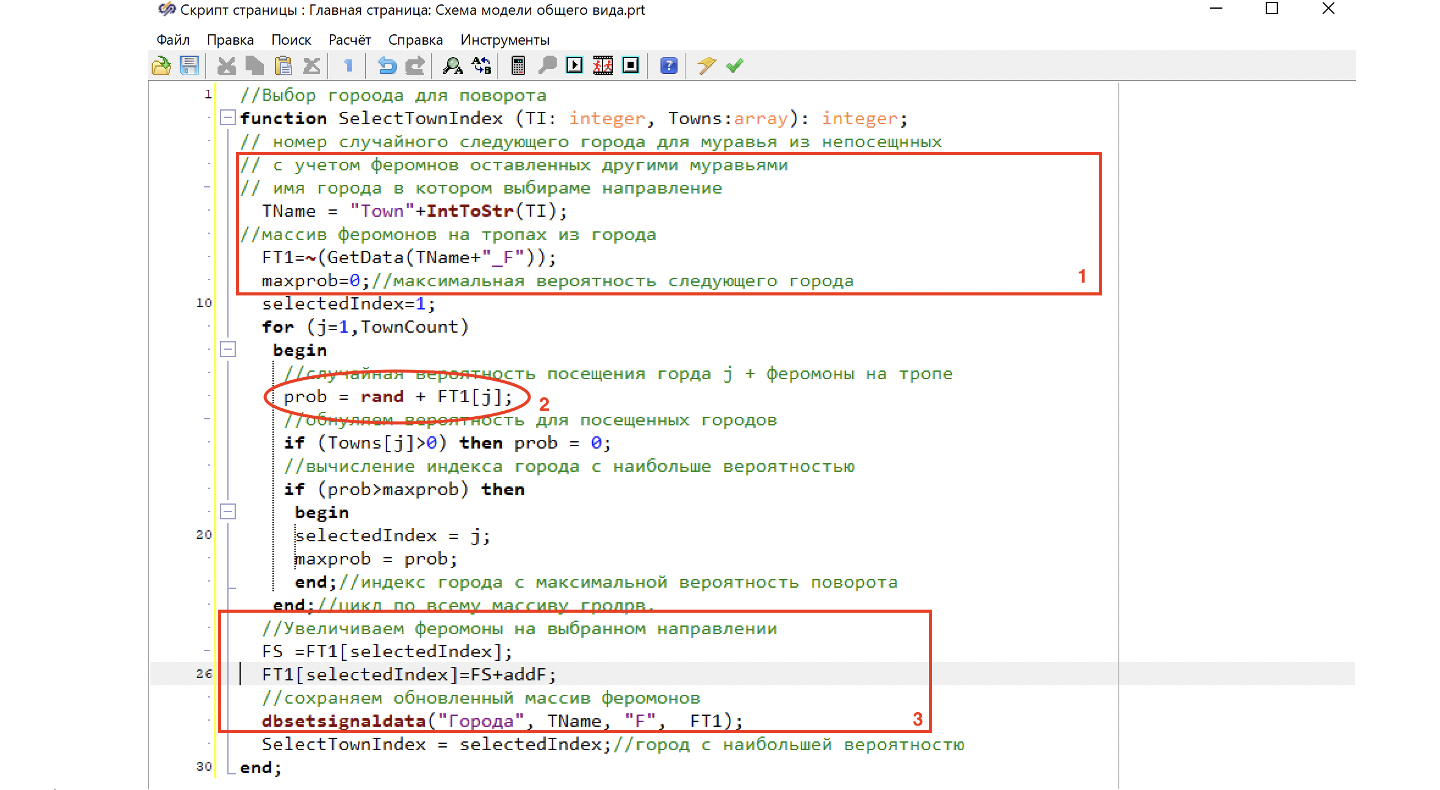
Иллюстрация работы алгоритма: запустим моделирование на 100 муравьев, 15 городов, 5000 секунд, в качестве добавки на каждом маршруте феромонов зададим значение 0.01. Результат такого моделирования - на рисунке 42.

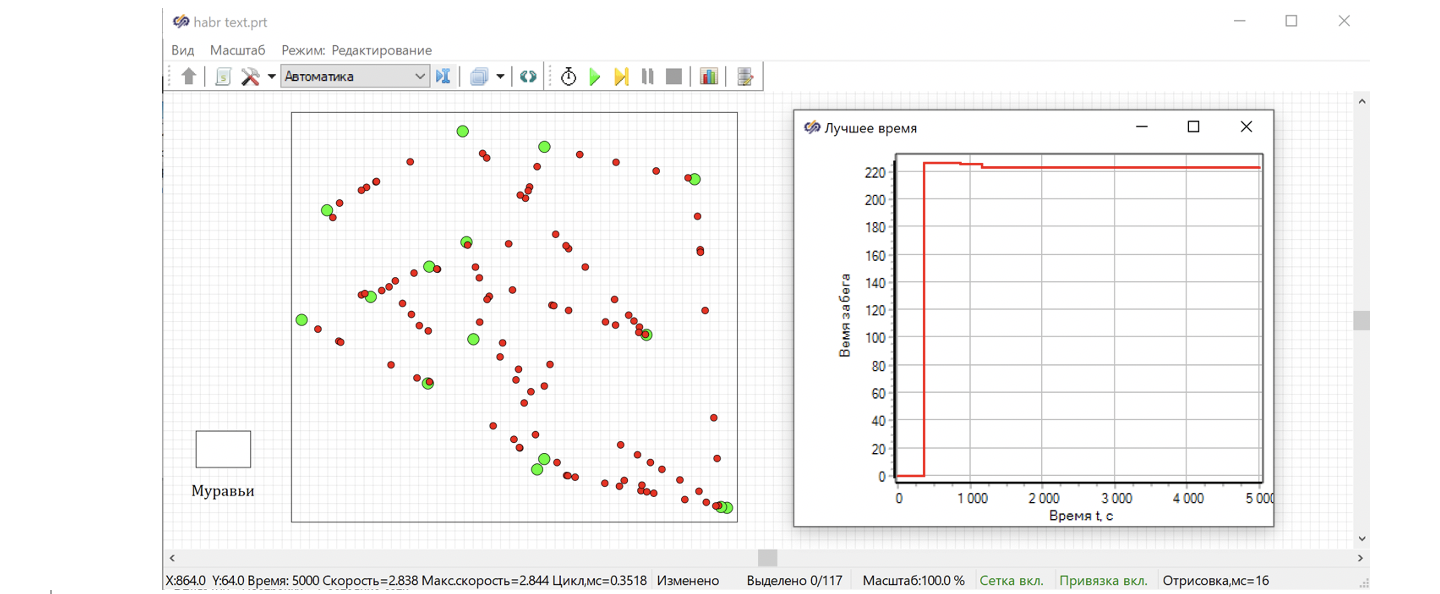
Судя по результатам, феромоны работают, и муравьи, изначально хаотически бегающие по полю, начали чуять следы. За 5000 секунд наши агенты протаптывают тропы и начинают двигаться стройными колоннами по одному. Сравните с рисунком 37, там по окончании расчёта все муравьи рассыпаны по всему полю и продолжают хаотично бегать, вместо того чтобы, как говорят немцы «die erste kolonne marschiert», как на рисунке 42.

Но видно, что это никак не помогает сократить общее время пробега. Муравьи просто начинают повторять первый попавшийся маршрут: куда случайно повернул первый муравей, туда потом и поворачивают все остальные, и время прохождения не меняется. Лучший результат – 221 секунда.

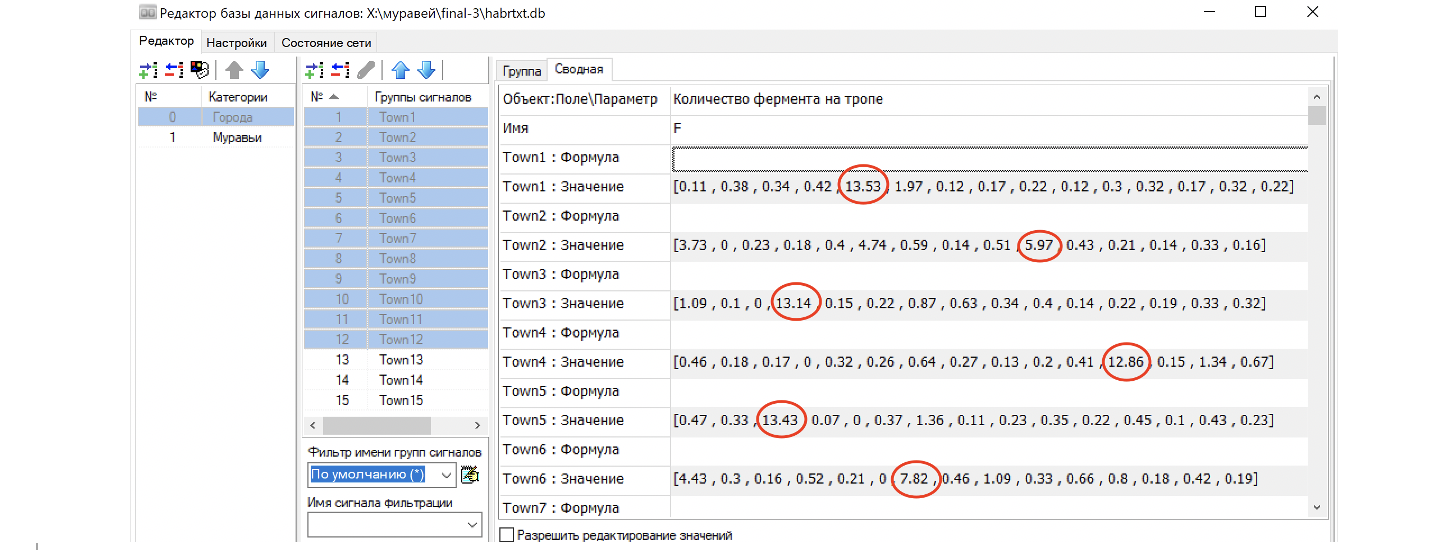
 Если посмотреть на массивы фермонов по маршрутам видно, что в каждом городе формируется за счет повторения поворотов предпочтительное направление, уровень феромонов которого исключает другие повороты. (См. рис. 43)

Добавляем испарение феромонов

Для того, чтобы алгоритм заработал, необходимо добавить испарение феромонов. Основная идея состоит в том, что муравьи оставляют феромоны, на всех тропах, но из-за испарения те тропы, которые длиннее, теряют больше феромонов, чем короткие, на которых феромоны чаще обновляются, поскольку муравьи проходят их быстрее. 

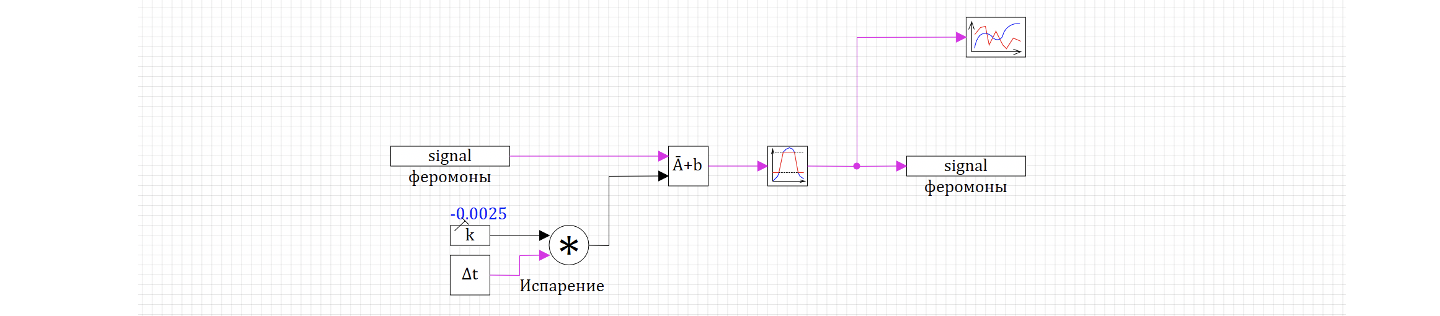
Схема испарения будет простая: мы соберем всем феромоны в один вектор и будем на каждом шаге интегрирования уменьшать на заданную величину - скорость испарения. Схема расчета испарения представлена на рисунке 44.

Также добавим ограничитель: минимальное количество феромонов = 0, и максимальное равное 10, для оценки скорости накопления.

Остается вопрос: каким образом подобрать скорость испарения. В первом приложении скорость выбирается таким образом, чтобы следы полностью испарились через 50 секунд модельного времени. Запускаем на расчет, установив время моделирования 25000. За это время 1000 муравьев пройдут порядка 10 000 вариантов маршрута.

Первый вариант:

добавка феромонов - 0.0025, 

скорость испарения - 0.00005

При таких условиях муравьи снова выстраиваются в колонны, максимальный рекорд принадлежит тому же самому муравью под номером 97!!!! 

На этот раз рекорд прохождения маршрута составил - 169. 839 секунд.

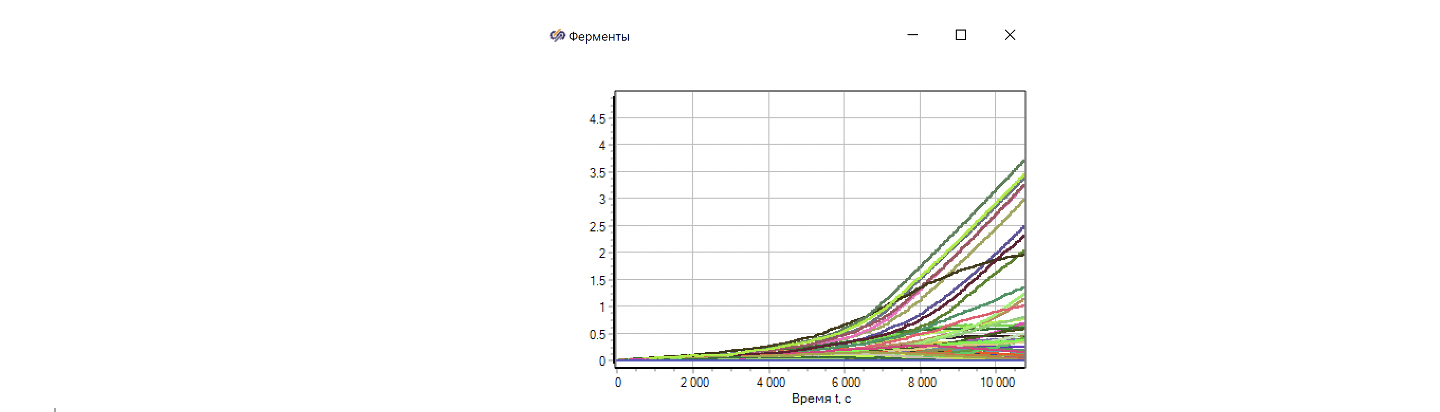
Однако, если посмотреть на график, то снижение было похоже случайным, примерно после 3000 секунды расчета. (см. рис. 45)

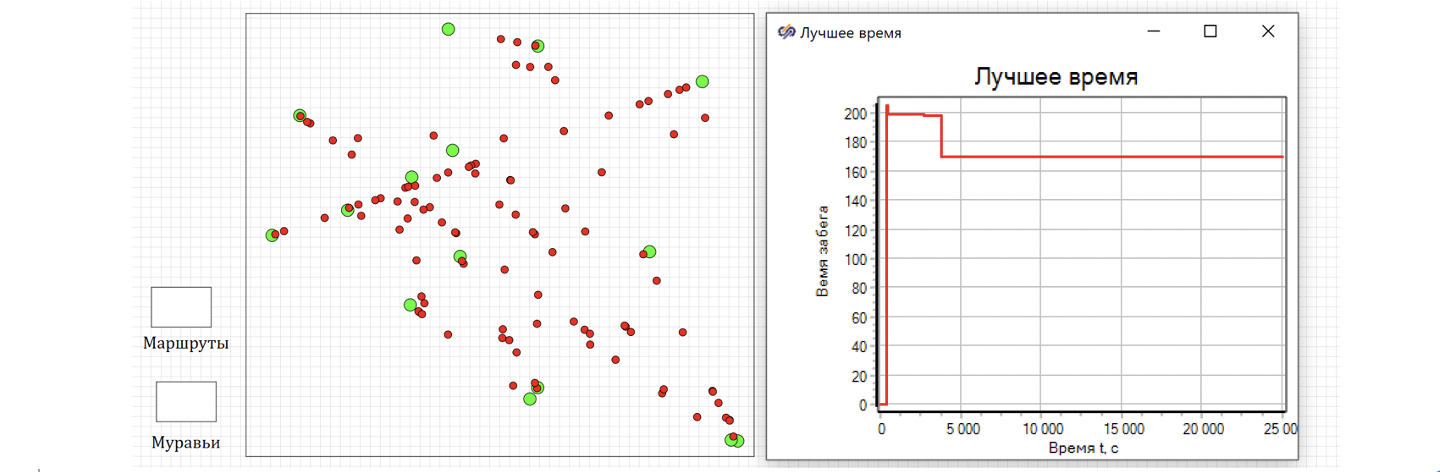
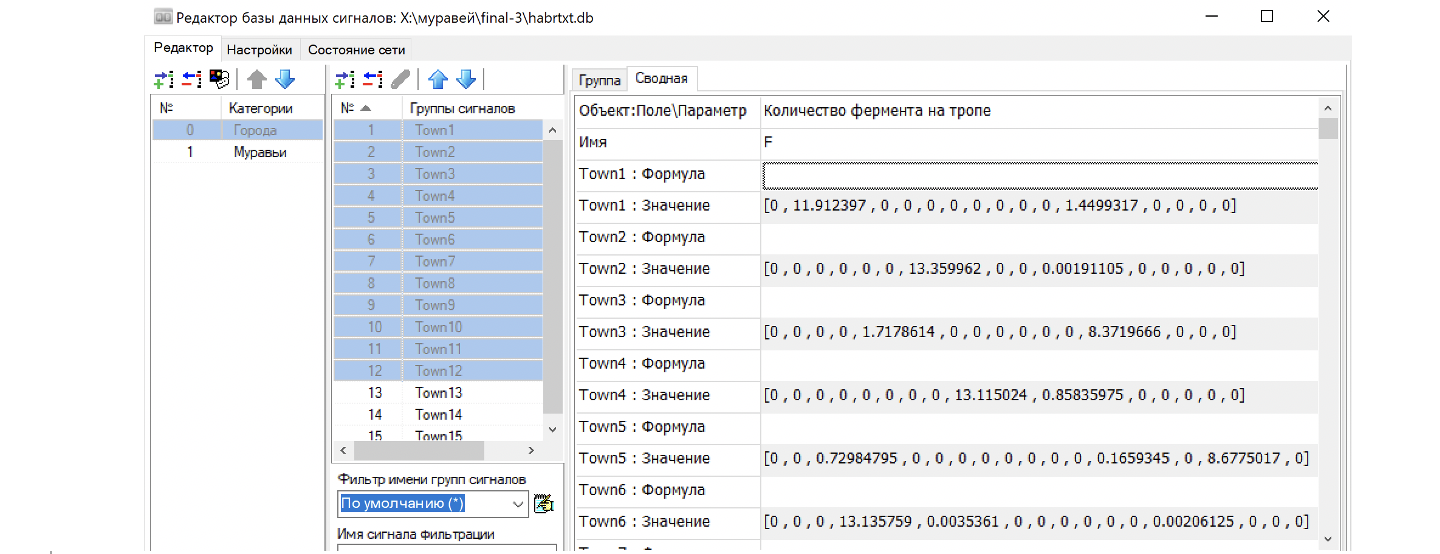
Если посмотреть на график феромонов на тропах, то видно, что после 5000 секунд расчёта феромоны концентрируются на определенных маршрутах и в дальнейшем только растут (см. рисунок 46). После этого происходит фиксация маршрута, все муравьи поворачивают в один и тот же поворот, выстраиваются в колонны и альтернативные пути уже не рассматриваются. Это же видно в базе данных, где феромоны в городе практически везде равны нулю, а значит агент-муравей, попав в город, всегда поворачивает в одну сторону.

Хакнем вселенную!

Честное моделирование не получилось, муравьи бегают, как настоящие по тропам, друг за другом, но не хотят вычислять кратчайшее расстояние (твари ползучие!). Придется подсмотреть решение в википедии. Формула для вычисления вероятности поворота там включает в себя расстояние между городами. С точки зрения честного моделирования движения муравьев, это нелогично. Откуда муравей знает будущее расстояние заранее? Чтобы отмерить нужное количестве феромонов? У него же нет Яндекс карт, у него и телефона то нет! Конечно, он не знает, и эти ученые только путают своим названиями «муравьиная тропа». Нет таких муравьев в природе!

Но у нас мир цифровой, и мы можем легко сделать муравья-оракула. Пусть он видит будущее, знает расстояние до следующего города и меняет количество феромонов в повороте.

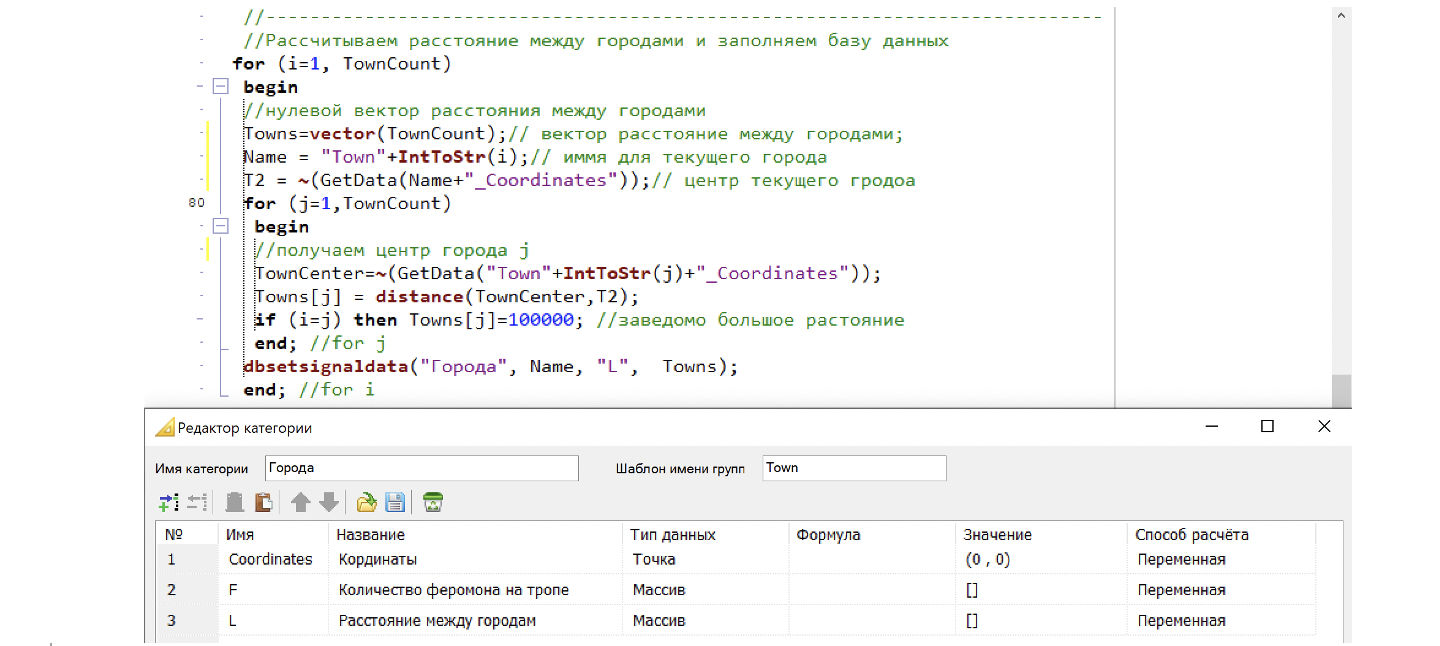
Усложним формулу для расчета количества феромонов на поворотах. Чем длиннее маршрут между городами, тем меньше феромонов оставим на тропе. Для этого после инициализации городов нам нужно дополнить массив с расстояниями до каждого города и учитывать этого расстояние при расчете добавки феромонов в расчёте поворота муравья. Расстояния между городами добавим в базу данных сигналов.

Код расчета расстояния при инициализации и вид базы данных сигналов представлен на рисунке 48.

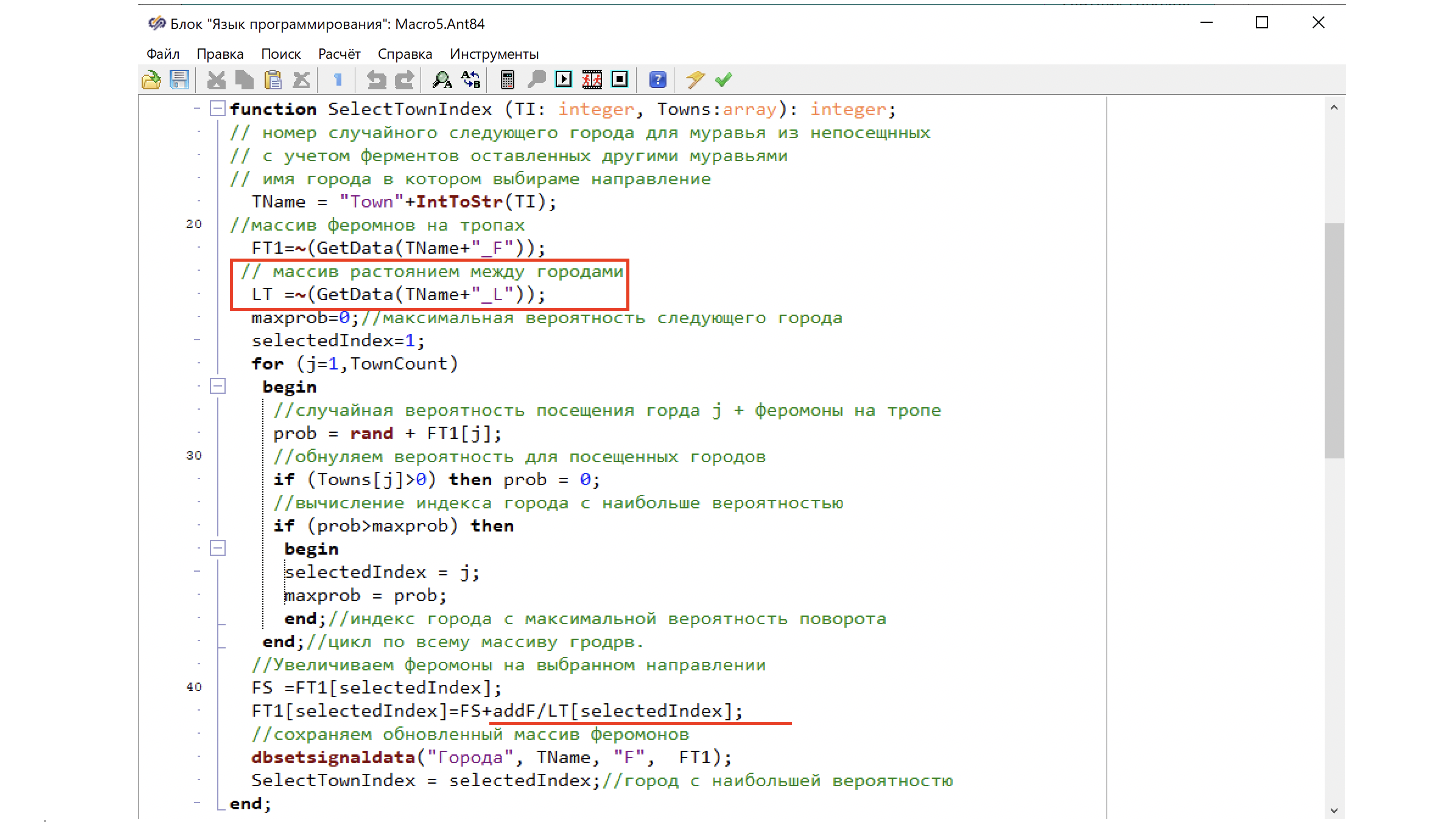
Полученный массив расстояний между городами используем при вычислении поворота. Практически нам нужно просто разделить добавленные феромоны на расстояние до выбранного города. (см. рис. 49).

Муравьи оракулы находят кратчайшую путь

Использование расстояния для выбора направления движения значительно улучшило результат работы алгоритма. Муравьи-агенты-оракулы смогли найти пути обхода всех городов за 121.55 секунд, что значительно лучше первых вариантов.  (194, 221, и 169 секунд)

Результат поиска лучшего пути представлен на рисунке 51.

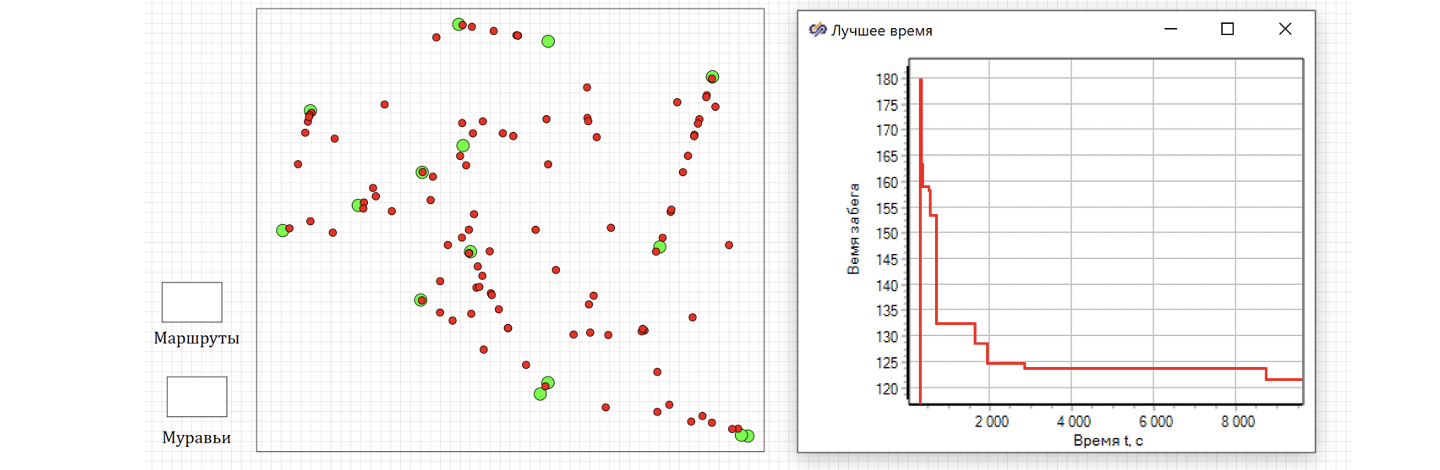
Выводы

Ученые нас обманывают: алгоритм «муравьиная тропа» работает не так, как в муравейнике!

Модели агентов в среде динамического моделирования создавать можно, и они даже работают. Векторный расчет и база данных сигналов делают свое дело.

Количество кода получилось ненамного больше чем в AnyLogic. 

Самая большая сложность при создании таких моделей – переключение в мозгах разработчика между пошаговой отладкой кода скрипта и отладкой во времени функциональной блок-схемы. Например, необходимо помнить, какой сигнал по линии передается до и после выполнения скрипта, особенно когда используются переключение или сброс начального состояния интеграторов. Совсем не очевидна последовательность работы блоков на графической схеме.  

В AnyLogic эти проблемы, очевидно, отсутствуют за счет привязки кода к событиям в схеме автомата. 

Ответ на вопрос: 

— Можно ли реализовать методы агентного моделирования в среде динамического моделирования?

— Можно, но осторожно!

Модель для исследования можно взять здесь...

Видео с демонстрацией работы моделей: