Всем привет, хочу с вами поделиться небольшим туториалом по работе в программе STATISTICA 10.0. Если кто из вас хочет познакомиться с теорией вероятностей или с математической статистикой, то эта программа одна из лучших в своей сфере. В этой статье я не буду приводить сложные (и не очень) формулы, которые нам расписывали на лекциях в институте, а попытаюсь пошагово показать как работать с данными и как проводить их анализ и визуализацию на примере.
Для начала небольшой ввод в теорию. Нормальным называется распределение вероятностей, которое для одномерного случая задаётся функцией Гаусса. Нормальное распределение играет жизненно важную роль во многих областях знаний. Случайные величины подчиняются нормальному закону распределения, когда на них влияет большое количество случайных факторов, что является типичной ситуацией при анализе данных. Поэтому нормальное распределение служит хорошей моделью для многих практических процессов.
И да, хотел сказать, что у меня версия программы на английском языке, но это не составит больших трудностей для нас. Первым делом создадим таблицу нужного объема. В верхней панели находим кнопку New и в окошке вводим возле Number of variables число 1, а возле Number of cases число 100 и нажимаем ок. Появляется пустая таблица, развернём её, чтобы она стала во весь экран и давайте её заполним случайными значениями. Для этого в верхней панели находим вкладку Data и дальше нажимаем на опцию Specs (Спецификации). В окошке выбираем нашу переменную (var1), внизу нажимаем на кнопку Functions и в правой части ищем функцию RndNormal (их там много, так что сразу скроллим до буквы R) и выбираем её двойным щелчком по имени функции. В текстовом поле появляются надпись =RndNormal( . Далее в скобку пишем любое положительное число(но не слишком большое, например <5), закрываем её, ставим знак плюс и любое число(например число месяца). В результате получить запись такого вида: =RndNormal(1) + 5 , нажимаем Ок и в вышеуказанном столбце таблицы появятся нужные числовые данные.
Оцениваем параметры распределения. Параметры распределения данных известны (они были заданы выше). Но на практике они бывают неизвестными. Их оценивают по выборке. Для создания впечатления о точности таких оценок следует их сравнить с известными значениями параметров. Для получения указанных оценок в окне Specs можно выбрать опцию Values/Stats. Появится окно с данными выбранного столбца, указанием относительно количества данных в столбце и вычисленными средним значением и среднеквадратическим отклонением рассматриваемых данных (в нижней части окна). Для более полного определения числовых характеристик данных и, в частности, проверки соответствия нормальному закону распределения следует выполнить более расширенный анализ. Для этого в верхней панели выбираем вкладку Statistics (Анализ) → Basic Statistics (основные статистики и таблицы) → Descriptive Statistics (описательные статистики). Задаем переменную для анализа (var1). В подразделе Advanced (Дополнительно) появятся названия дополнительных числовых характеристик выборки. Добавим галочки для median (медиана), skewness (асимметрия) и kurtosis (эксцесс). И нажимаем на кнопку Summary.

Для теоретического нормального распределения медиана и среднее значение совпадают, а асимметрия и эксцесс равны 0. Поскольку сгенерированные данные имеют нормальное распределение несколько приближенно, вычисленные значения удовлетворяют этим соотношениям приближенно, но большие отклонения не должны иметь места быть. Эксцесс – показатель остроты пика графика распределения. Асимметрия представляет собой числовое отображение степени отклонения графика распределения показателей от симметричного графика распределения. Если асимметрия больше 0, то чаще в распределении встречаются значения меньше среднего.
Пришло время для графической визуализации данных. Вновь воспользуемся модулем Descriptive Statistics (значок данного модуля находится в нижней левой части экрана). Выбираем подраздел Quick и нажимаем на Histograms. Появляется вот такая гистограмма:
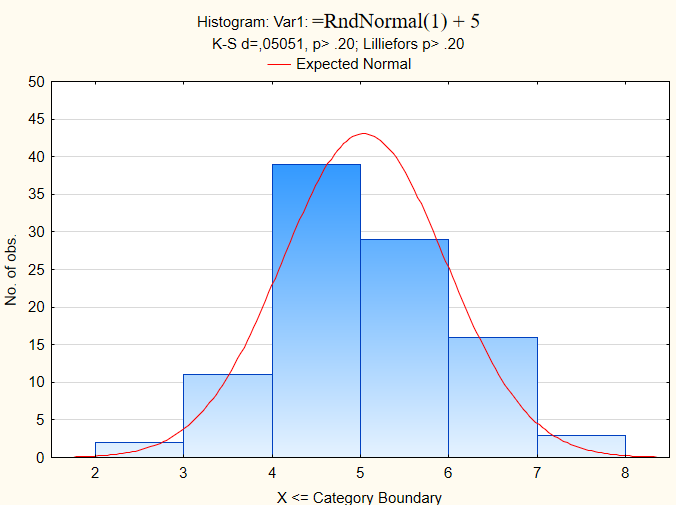
В гистограмме данные разбиты на интервалы и каждый интервал изображен в виде столбика.
Выделяем подраздел Options. В открывающемся меню добавляем галочку возле способа построения box-Whisker plot соответствующего принципу median/quartiles и возвращаемся в раздел Quick, выбираем опцию box & whisker plots. Получаем две диаграммы “Ящика с усами”.

Коробчатая диаграмма “Ящик с усами” состоит из прямоугольника, занимающего пространство от первого до третьего квартиля (от 25 до 75 процентиля). Линия внутри этого прямоугольника соответствует медиане. Кроме того, на коробчатой диаграмме отмечаются максимальное и минимальное значения, если только они не являются выбросами. Значения, удаленные от границ более чем на три длины построенного прямоугольника (экстремальные значения), помечаются на диаграмме звездочками. Значения, удаленные более чем на полторы длины прямоугольника, помечаются кружками.
Возвращаемся в меню Descriptive Statistics. Выбираем раздел Normality. В нём – диаграмма Stem & Leaf plot (ствол и листья).
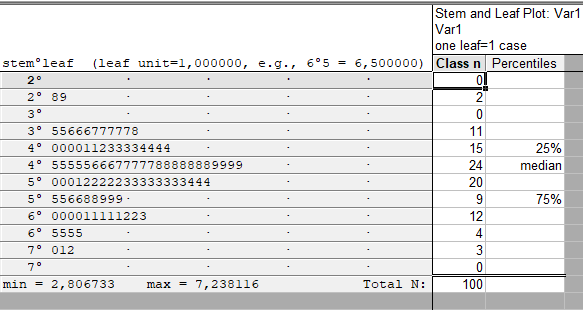
Диаграмма ствол и листья (или стебель и листья) представляет собой комбинацию гистограммы и табличного списка. Подобно гистограмме, в диаграмме ствола и листьев длина каждой строки соответствует количеству наблюдений, попадающих в определенный интервал. Но, сверх этого, на данной диаграмме выводится также наблюдаемое численное значение для каждого наблюдения. Для этой цели численные значения разбиваются на два компонента: ствол, представляющую собой первую цифру или группу цифр и листья — последующие цифры. Ствол соответствует тем разрядам численного значения наблюдаемой переменной, которые не изменяются, а листья — разрядам, которые изменяются в пределах избранного интервала.
Ещё один важный график это Q-Q plot (квантиль-квантиль график). Чтобы его получить в верхней панели выбираем вкладку Graphs → 2D → Quantile-Quantile Plots → Normal (Не забываем выбрать переменную). → Ок.
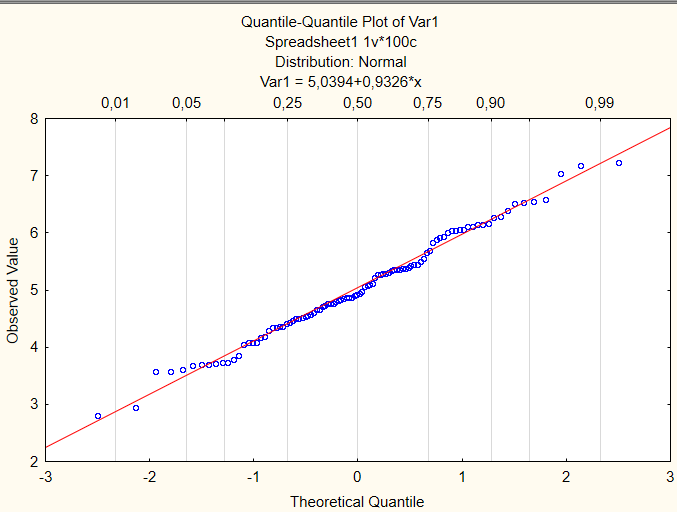
На этом графике показана связь между наблюдаемыми значениями переменной и теоретическими квантилями. Если наблюдаемые значения попадают на прямую линию, то теоретическое распределение хорошо подходит к наблюдаемым данным.
На этом всё. Знаю, что это только основа теории вероятностей и для знающих людей тут нет ничего нового или интересного. Я надеюсь, что этот туториал может быть хоть кому то полезен. Возможно я ещё напишу статью о хи квадрате или о множественной линейной регрессии и их анализе в программе Statisctica.

