Вы можете сказать, что один факт выбивается из этого ряда в заголовке, потому что он не так очевиден, как остальные. Еще лет 10-15 назад я бы никогда не подумал, что тут могут быть возражения, а сейчас уже и не удивляюсь, что приходится объяснять простые истины: дело в том, что планеты обладают очень большой массой, поэтому гравитация стремится придать им форму шара. Вот и все! Хотел бы на этом закончить статью и поблагодарить за внимание.

Хотел, но не вышло: как-то раз, находясь на одном из этих массивных шаров, я оставил комментарий и получил на него 2 ответа.

По сути @Vitalley и @Covert правы. Но насколько? Действительно ли требуется хранить в double? Давайте разбираться на примере JPEG почему он портит изображение и можно ли, хотя бы теоретически, избежать потерь. Впрочем, интерес представляет даже не сам JPEG, а возможность использования линейных преобразований для сжатия без потерь.

Сначала мы рассмотрим основные этапы JPEG и немного углубимся в некоторые из них, чтобы понять происходящие преобразования с математической точки зрения. Выясним когда именно происходит искажение информации. Покажем, что информация восстановима, если задать относительно низкий шаг квантования и найдем его максимальное теоретическое значение. Затем, для проверки, постараемся найти его практически. В завершение сделаем выводы о том, насколько реальна поставленная цель.

На следующей картинке я отметил все этапы на которых происходит потеря информации.

Все рассмотрим подробно кроме кодирования Хаффмана, так как это сжатие без потерь.

Преобразование RGB в YCbCr

По стандарту, кодер не занимается преобразованием цветовых пространств. Ему на вход подается изображение, уже разделенное на каналы. Для заданных каналов кодер выполнят субдискретизацию. Это означает, что вместо хранения цвета каждого пикселя небольшой группы (размером 2x2, 2x2, 4x2 и т.п.) будет храниться только одно — среднее этой группы. На практике почти всегда используется пространство YCbCr с последующей субдискретизацией. Почему? Хорошо, что я не в школе, и могу просто скопировать из Википедии:

Перевод в систему Y’CbCr позволяет передать информацию о яркости с полным разрешением, а для цветоразностных компонент произвести субдискретизацию, то есть выборку с уменьшением числа передаваемых элементов изображения, так как человеческий глаз менее чувствителен к перепадам цвета.

Так как при субдискретизации исходные значения теряются безвозвратно, то нам придется отказаться от ее.

Преобразование цветового пространства полностью обратимо пока мы храним дробные числа. Потери происходят из-за округления с которым еще можно поработать. Например, не округлять, а сохранять несколько двоичных цифр после запятой.

Пространства RGB и YCbCr выглядят так относительно друг друга:

Все цветовые каналы (R, G, B, Y, Cb, Cr) в неэкзотических вариациях JPEG являются 8-битными. Количество возможных цветов совпадает в обоих пространствах (2^24). Но если у большинства комбинаций (Y, Cb, Cr) нет соответствующей (R, G, B)-пары, значит у кого-то их две :( И даже больше. Однозначное восстановление с такими исходными данными невозможно.

Итак, перевод (R, G, B) в (Y, Cb, Cr):

В матричном виде:

Матричное представление будет использоваться и дальше, поэтому для понимания статьи желательно знать о матричном произведении, обратной матрице и т. п.

DCT

Каждый блок 8x8 каждого канала (обычно это Y, Cb, Cr) изображения подвергается двумерному дискретному косинусному преобразованию 2-го типа. Почему используется именно DCT я подробно описывал здесь. Рассмотрим, что оно означает.

Каждый блок может быть представлен в виде матрицы:

Сначала для каждого столбца независимо от других выполняется преобразование :

По следующей формуле, в которой — индекс столбца:

Такая формула может быть переписана в матричной форме: . Где и — вектор-столбцы, а значения матрицы аккуратно рассчитаны по вышеприведенной формуле:

Преобразование описывает переход новому базису. Каждая строка задает координаты базисного вектора. Вот они:

Одна из фичей этой матрицы — ортогональность. Это означает, что все базисные вектора ортогональны друг другу и их длины равны 1. То есть, такое преобразование описывает поворот плюс, возможно, зеркальное отражение. Это сохраняет евклидову норму векторов (то есть их длины, которые мы вычисляем по теореме Пифагора).

Вместо одного вектор-столбца в можно подставить сразу все столбцы, и тогда получим: .

Далее нужно выполнить такое же преобразование , но уже для строк. Нам известно как это провернуть для столбцов, поэтому транспонируем , преобразуем, а затем транспонируем еще раз: .

Сейчас провернем такой трюк. Получившуюся матрицу векторизуем, то есть последовательно выпишем все столбцы в один. И затем применим формулу , где — произведение Кронекера:

Матрица имеет размер 64 на 64. Каждая ее строка представляет 64 комбинации произведений попарных значений двух «волн» из предущей картинки. И если их выписать в виде матрицы 8x8, то получится двухмерная волна. Разные строки дадут разные частоты по x и y. Вот они все на рисунке.

Описанное преобразование можно представить как нахождение корреляции блока изображения с каждой из этих волн.

Одно из свойств произведения Кронекера — если и ортогональные матрицы, то тоже является ортогональной. Формулу обратного преобразования можно получить умножив обе части на транспонированную матрицу: . Так как для ортогональных матриц справедливо, что , то получаем: .

Почему происходят потери?

Меня давно преследует идея создания максимально гибкого JPEG-кодека, позволяющего пользователю задавать свои таблицы Хаффмана и квантования. Во-первых, потому, что это офигенно, вот почему. Во-вторых, такой кодек сможет имитировать другие кодеки (и фотоаппаратов тоже), но это отдельная тема. В-третьих, особенно если выйти за пределы стандарта, это полезно для исследований. В частности, можно предусмотреть изменение фиксированного размера блоков 8 на 8. Можно сделать даже 2 на 1. Это бесполезно с практической точки зрения, но зато каждый такой блок из двух пикселей (одного канала) можно наглядно представить в виде вектора координатной плоскости и наглядно увидеть преобразования этого вектора.

DCT для такого простого случая будет выглядеть так:

Представим, что первый пиксель имеет цвет 3, а второй — 2. После преобразования получим (3.536, 0.707). Наименьший шаг квантования в JPEG равен 1, то есть это просто округление: (4, 1). После восстановления: (3.536, 2.121), значит первый пиксель — 4, второй — 2.

Если бы мы квантовали с большим шагом чем 1, то расхождение могло оказаться еще значительнее. Относительно недавно я рассматривал, что происходит при различных шагах квантования. Но тогда все они были целыми, не меньше единицы, а сейчас наоборот, будем уменьшать.

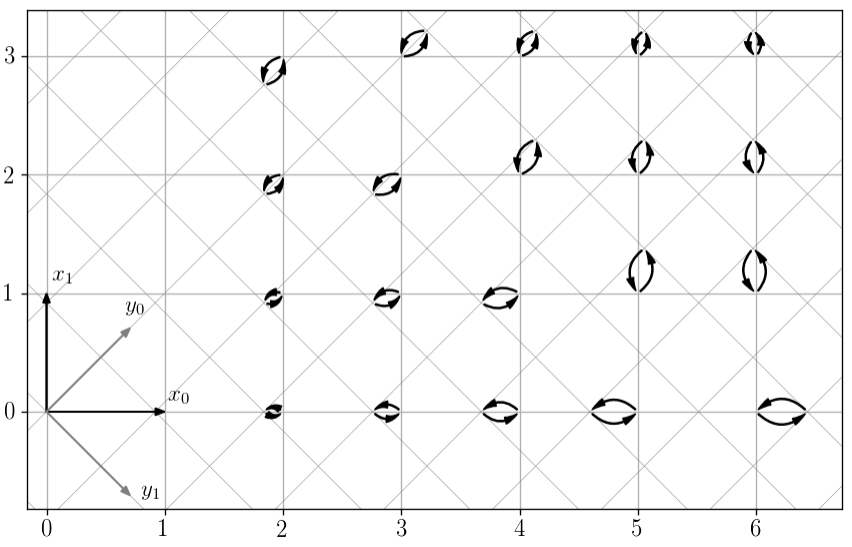
Глядя на координатную сетку на рисунке выше, можно сделать грубую прикидку. Квантованная точка не должна отдалятся более чем на 0.5 от исходной. Но если исходная точка оказывается в центре ячейки сетки пространства , квантованная отдаляется на половину диагонали квадрата (0.707). Значит, если квантовать с более мелким шагом не превышающим 0.5/0.707 = 0.707, то потерь удастся избежать. На следующем рисунке показан шаг 0.65 (при 0.707 узлы сеток совпадают и получается не наглядно) для нескольких исходных точек.

Упрощенный код примитивного кодека:

step = 0.65
C = sqrt(2) / 2

def write(x0, x1):
    y0 = C * (x0 + x1)
    y1 = C * (x0 - x1)
    save_to_file(round(y0 / step))
    save_to_file(round(y1 / step))    

def read():
    y0 = load_from_file() * step
    y1 = load_from_file() * step    
    x0 = round(C * (y0 + y1))
    x1 = round(C * (y0 - y1))
    return x0, x1
    
x = (3, 2)    
write(*x)
xx = read()
assert xx == x

Разумеется, уменьшение шага не дается бесплатно. Чем он меньше, тем больше множество значений, которые нужно хранить. Уменьшение в два раза эквивалентно увеличению на один бит.

В настоящем JPEG используется 64-мерное пространство, поэтому половина диагонали 64-мерного гиперкуба равна . Получается, что нужно сделать шаг квантования 0.125, то есть хранить 3 бита после запятой. Но это не доказательство, конечно, а просто прикидка.

Оказалось, что это верная оценка для произвольного 64-мерного ортогонального преобразования. Но для DCT максимальный шаг квантования немного больше.

Максимальный шаг квантования

Итак, пусть — исходный вектор с целыми значениями, — матрица преобразования (RGB в YCbCr или DCT), — функция квантования, — округления. После квантования получаем вектор . Для DCT именно эти значения сохраняются в файле. При восстановлении исходных значений выполняем обратное преобразование: .

Наша задача — научиться восстанавливать без потерь, то есть сделать справедливым равенство для любого вектора X. Единственное «неизвестное» в этом уравнении — функция квантования. Очевидно, что можно не квантовать (то есть задать ) и тогда, учитывая , уравнение схлопнется до , а значения X и так целые. Формально, это решение, но оно, очевидно, не подходит.

Что вообще следует из записи ? То, что ни один элемент вектора не отличается от соответствующего элемента более чем на 0.5. Или эквивалентно: максимальная абсолютная разность элементов и не больше 0.5:

Хмм, да это же кисулькен норма (ну или расстояние) Чебышева.

Получается, что из следует . Умножим выражение под нормой на (мы можем так поступить потому что это равносильно умножению на единичную матрицу, то есть результат не меняется):

Обозначим . Вектор представляет отклонение при квантовании в преобразованном базисе. Итак, наше неравенство приобретает следующий вид:

Это должно выполняться для любого . А каким он может быть? Очевидно, разность между квантованным и исходным значением не превышает половины шага квантования. Так, если шаг квантования равен s, то . В наших интересах найти наибольший шаг, удовлетворяющий . На следующем рисунке показан максимальный допустимый шаг.

Уменьшать шаг неэффективно. Но увеличение, даже совсем чуть-чуть, может привести к нарушению нашего основного неравенства.

Здесь мы можем выполнить следующую грубую прикидку для ортогонального преобразования. Евклидова норма вектора не меньше нормы Чебышева. Поэтому, если справедливо , то будет верно и . А так как ортогональное преобразование сохраняет евклидову норму, то . На рисунке видно, что при таком подходе шаг квантования уменьшился из-за того, что мы избавились от заданного базиса и перешли к произвольному ортогональному.

Воспользуемся обеими нормами:

Отсюда максимальный шаг равный . Для получим 0.125, как и предполагали в начале статьи.

Можно точнее? Да. Возвращаемся к и запишем его так:

Чтобы максимизировать сумму, нужно максимизировать каждое слагаемое. Для этого нужно в качестве подставить с тем же знаком, что и у (не тот знак приведет к вычитанию). Или же подставить плюс и взять по модулю:

Считаем:

import numpy as np
from scipy.fftpack import dct

def max_step(D):
    return 1 / np.max(np.sum(np.abs(D), axis=1))
  
YCbCr2RGB = [[1, 0, 1.402], [1,-0.344136,-0.714136], [1,1.772,0]]

# Генерируем матрицу для одномерного DCT
# Вместо X в формуле dct(X) = DX подставляем единичную матрицу
# И получаем D = dct(I)
D_8 = dct(np.identity(8), norm='ortho', axis=0)

# Оператор Кронекера
D_8x8 = np.kron(D_8, D_8)

# Для DCT обратная матрица равна транспонированной
ID_8x8 = D_8x8.T

print('YCbCr2RGB:', max_step(YCbCr2RGB)) # 0.36075
print('IDCT:', max_step(ID_8x8))         # 0.14328

C YCbCr понятно, 1 / (1 + 1.772) = 0.36075. Теперь давайте вычислять 0.14328 для DCT. Заметим, что строки матрицы — это столбцы . Если представить индекс столбца в виде :

Тогда, например, для нулевого столбца:

Это выражение можно упростить с помощью тождества Лагранжа:

Подставляем и немного упрощаем. Итого: . В принципе, котангенс тоже можно вычислить точно, но с кучей радикалов.

Максимальный шаг: . Такое же значение получается и для других столбцов матрицы.

Проверяем 0.36075

Выполнить проверку максимального отклонения при преобразовании цветовых пространств можно просто путем перебора всех значений (R, G, B):

M = np.array([[ 0.299,     0.587,     0.114   ],
              [-0.168736, -0.331264,  0.5     ],
              [ 0.5,      -0.418688, -0.081312]])
IM = np.array([[1,  0,         1.402   ],
               [1, -0.344136, -0.714136],
               [1,  1.772,     0       ]])

def quant(x, step):
    return np.round(x / step) * step

def ycbcr_d_inv(x, step):
    y = np.dot(IM, quant(np.dot(M, x), step))
    return np.max(np.abs(y-x))

step = 0.36075
max_d = 0
for r in np.arange(0,256):
    for g in np.arange(0,256):
        for b in np.arange(0,256):
            d = ycbcr_d_inv([r,g,b], step)
            if d > max_d:
                max_d = d

print(max_d) # 0.499517

Действительно, выбранный шаг почти идеален. Наибольшее отклонение очень близко к 0.5, но не превысило его, поэтому при округлении мы восстановим исходные значения.

Проверяем 0.14328

Представьте квадратный город километр на километр. У него есть центральный район размером пол- на полкилометра, и окраина, площадь которой равна половине площади всего города — 0.5 кв. км. Эти районы двухмерного города изображены на рисунке.

Площадь центра равна 0.25, а ширина окраины — примерно 0.146. Но что если город представляет собой гиперкуб? Тогда его объем — 1 км^N, а остальные значения для некоторых размерностей в таблице:

       N  Объем центра (км^N)  Ширина окраины (метров)
       1      0.5                  250 
       2      0.25                 146
       3      0.125                103
       4      0.0625                80
       8      0.0039                41
      16      1.5e-05               21
      32      2.3e-10               11
      64      5.4e-20                5

В 64-мерном городе центр стал занимать невообразимо маленькую часть всего города, несмотря на его большой линейный размер. А половина горожан живет в тонкой 5-метровой оболочке на окраине.

Но окраина очень неоднородна. Где-то до центра всего 500 метров, но в среднем подальше. Дальше всего до одного из 2⁶⁴ углов. По прямой из центра не очень далеко — 4 километра. Но если застройка (гипер-)прямоугольная и передвигаться можно только по улицам параллельным осям, то придется преодолеть 32 километра. Но окрестности углов занимают мизерную долю. Даже если предположить, что их размер 333 метра, то в двухмерном городе они займут 4/9 площади, а 64-мерном всего .

Эти контринтуитивные размышления — частные случаи проявления проклятия размерности. Для нас они интересны тем, мы хотим найти наибольшее отклонение при квантовании, а для этого нужно чтобы узел сетки квантования оказался недалеко от одного их углов гиперкуба. Наверно это можно сделать аналитически, но тут мои полномочия всё. Мы можем перебирать различные векторы и надеяться на удачу, которой не будет. Потому что вектор отклонения будет вести себя примерно как случайно распределенная величина. Посмотрим сначала на распределения расстояний от случайной точки до центра куба для разных размерностей (в логарифмическом масштабе):

def get_data(n):
    data = []
    for _ in np.arange(0, 1000000):
        x = np.random.uniform(-0.5, 0.5, size=(n))
        data.append(np.linalg.norm(x))
    return data

Теперь перейдем к распределению отклонений DCT. Здесь считается расстояние Чебышева, для «наклоненного» гиперкуба, поэтому распределение немного другое. Это можно можно приблизительно проиллюстрировать на плоскости:

def quant(x, step):
    return np.round(x / step) * step

def dct2d_d_inf(x, step):
    y = np.dot(ID_8x8, quant(np.dot(D_8x8, x), step))
    return np.max(np.abs(x-y))

step = 0.14328
data = []
for _ in np.arange(0, 1000000):
    # В Jpeg из Y, Cb, Cr вычитается 128
    x = np.random.randint(256, size=(64)) - 128
    data.append(dct2d_d_inf(x, step))

plt.clf()
plt.xlim(0, 0.5)
plt.hist(data, 30, log=True)
plt.show()

Наибольшее значение, которое я смог найти — 0.318618 для вектора [79192, 0, 0, ..., 0]. Но исходными значениями для DCT в Jpeg являются Y, Cb, Cr уменьшенные на 128, то есть от -128 до 127. И для них все перебранные отклонения оказались меньше 0.25.

Выводы

Наш проект «JPEG без потерь» потребует серьезных жертв:

• Не использовать субдискретизацию.

• Квантовать значения Y, Cb, Cr с шагом 0.36075. Это плюс 2 бита.

• Квантовать коэффициенты DCT с шагом 0.14328. Плюс еще 3 бита.

Итого к исходным 8 битам добавляется еще 5, итого 13. Любопытно, что стандарт помимо обычного 8-битного JPEG , также описывает и 12-битный. Раз уж мы зашли так далеко, то интересна сама принципиальная возможность использовать его для нашей цели. Но нужно где-то сэкономить 1 бит. Способы такие:

• Самый разумный — кодировать сразу в RGB, так как без субдискретизации и таким квантованием оно бессмысленно.

• Не округлять Y, Cb, Cr, тогда шаг квантования составит 0.36075 * 0.14328 = 0,05169. Это бита. Ну, почти «запихнули».

• Надеяться никогда не встретить отклонение превышающее 0.5 при квантовании DCT-коэффициентов с шагом 0.25.

Поддержка 12-битного JPEG встречается крайне редко. Я нашел только libjpeg и один платный конвертер (в бесплатной версии ставит вотермарку — для тестов пойдет).

Разумеется, все эти выводы неприменимы на практике. Даже обычный JPEG с максимально высоким качеством почти не используется, так как теряются основные фичи алгоритма, что приводит к слишком большому размеру файлов. А для 12 битов размер увеличивается в 1.5 — 3 раза и уже проигрывает png. Впрочем, эти выводы могут быть полезны при разработке алгоритма сжатия без потерь, основанные на DCT.

Напоследок, краткие правила для минимизации потерь:

1. Не используйте JPEG.

2. Если используете — сохраняйте в нем только окончательный вариант, не пересохраняйте.

3. Если пересохраняете — выбирайте то же самое качество сжатия, не уменьшая и не увеличивая.

4. Если пересохраняете и изменяете качество сжатия — не изменяйте размер изображения.

5. Если пересохраняете и изменяете размер — не удивляйтесь.