Программист обязательно ставит на тумбочку у кровати два стакана: один полный, на случай, если он проснётся и захочет пить, а другой пустой — вдруг он не захочет. Так гласит известный анекдот. Но в реальной жизни часто работают законы Мерфи, и предусмотренные планы рушатся. Что же делать программисту на случай, если он проснётся и не поймёт, хочет он пить или нет?
Наверное, самый зубдробительный для меня темой в курсах Высшей Математики была Алгебра. Это не та милая, ламповая школьная алгебра, плавно переходящая в любимые мной диффуры, да ещё если в исполнении Киселёва... Нет. Это множества, дурацкие полуочевидные теоремы, странные термины, идеалы, ¡алгебры!, кольца (йуный ум скорее задумается об обручальных, право слово). В общем, за исключением полей, для нас, агрономов, это были вещи настолько же нудные, насколько и бесполезные. Прямо как с Военной Кафедрой: есть, ¡есть! методики преподать даже самый интересный и увлекательный предмет так, чтобы всем слушателям без исключения просто сводило скулы от скуки.
А можно ли позорный недуг в подвиг определить? В конце-концов, скучность алгебры в её совершенной оторванности от жизни, абстрактности, приближающейся к известному плагиату картины А. Алле «Combat de negres dans une cave, pendant la nuit». Абстрактность, абстрагирование, обобщение, «для всех вместе и никого в частности...» Вроде бы общие понятия на то и общие, что должны быть применимы просто везде?
«Ну вот и попробуй, примени.» — с этими словами к себе, я и начну рассказ.
Решётки и полурешётки
Всего полгода назад, благодаря чудеснейшему сайту https://github.com/true-grue/Compiler-Development ( @true-grue, ¡СПА-СИ-БО!), а также одноимённому каналу, я начал познавать чудесный мир производства группы А для ИТ. Выражаясь проще, полупрочёл чудесный учебник Anders'а Møller'а „Static Program Analysis“ (https://cs.au.dk/~amoeller/spa/). Увы, не до конца. В оправдание могу лишь прохрипеть как Бильбо у Голлума «Время! Время!». Но, как сказал Пендальф другому хоббиту, «самую суть-то ты ухватил».
A. Møller в книге блестяще сводит различные варианты анализа программ (почти всё, за исключением вывода типов), к работе с разнообразными решётками. Тут нам и анализ знаков, и определение неинициализированных переменных, и liveness анализ... И всё это разное великолепие сводится к решёткам, то есть частично-упорядоченным множествам, у любой пары элементов из которых есть точные верхняя и нижняя граница.
Кстати, странно, что ЧУМы не изучаются в школе — во-первых, они приучают к мысли, что не всегда можно найти «самое лучшее» (типичный вопрос у малышей какая машина лучше?), а во-вторых, название смешное: вроде высоколобые математики, а у них ЧУМ. Может и яранга с оленями?
Более формально, решётка — это множество, на котором определена операция ≤, но не обязательно между любыми двумя элементами с тремя свойствами: транзитивностью (a ≤ b, b ≤ c => a ≤ c), антисимметричностью (a ≤ b и b ≤ a => a=b) и рефлексивностью (a ≤ a). Причём для любых двух элементов a, b, даже если они не сравнимы, есть элемент c, что не меньше их обоих: a ≤ c и b ≤ c. А также существует d, который не превосходит a и b: d ≤ a, d ≤ b.
Эти c и d называются верхней и нижней гранью, а самые «поджимающие» пару a, b, то есть самый «маленький» из разных c и самый «большой» из разных d — точной верхней и точной нижней гранью. Для решётки, собственно, необходимо наличие именно точных граней.
В принципе, и в Википедии на данный момент что-то более-менее правильное написано, но у Møller'а тема раскрыта сильно лучше. Наверное, где-то ещё лучше, но нам достаточно буквально самых начал.
Ладно, всё это слова, мы же любим картинки. Картинки для решёток рисуются исключительно просто, это так называемые диаграммы Хассе. Точки — это элементы множества, рёбра — отношения ≤ (какие есть), а кто выше, то и больше (так, по крайней мере, у математиков в северном полушарии). Вот примеры решёток:
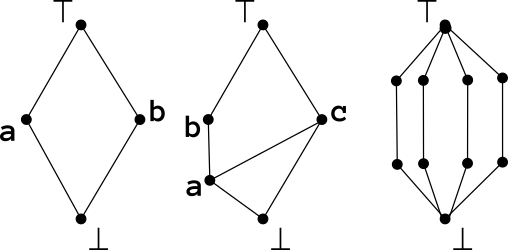
А вот примеры ЧУМ, которые не решётки (последняя решётка, но не полная):

А вот полностью линейно-упорядоченное множество вроде ℝ или ℕ на такой диаграмме будет крайне скучно рисовать, поэтому я не буду. @ReadOnlySadUser — вот вам и упражнение на понимание. :-)
Ну решётки — вещь чудесная, только обещал я использовать лишь половину, а не целую решётку (как говорят в ФТИ РАН „вы столько времени занимаетесь полупроводниками, пора бы и на полные проводники перейти“). Полурешётка — это просто ЧУМ, где есть только верхние грани или только нижние грани. Вот, к примеру:
Совершенно естественно решётки появляются когда у нас есть какое-то множество и мы рассматриваем его всевозможные подмножества. Тут я совершенно беспардонно тисну картинку у Møller'а для множества {0,1,2,3}, потому что Андерс об этом никогда не узнает:

Всё это замечательно, но где же практика, где же слайды? Честно говоря, я всю жизнь пытался держать от зубодробительной практики вроде применений 1С в сельском хозяйстве как можно дальше, поэтому пример может показаться наивным.
Классификация
Допустим, у нас есть пушистый чёрный кот, который ест только рыбу (а пить предпочитает валерьянку, но это неважно). А в добавок к нему есть собака и черноухий кролик. Собака, понятно дело, ест и рыбу, и мясо, а кролик — только морковку. Если мы, чтобы закодировать содержимое холодильника, введём тип

data Еда = Мясо
| Рыба
| Морковкато этот тип не будет в полной мере «описывать предметную область». Но вот если мы
достаточно механически начнём строить полурешётку на этом базисе, введя
дополнительно Рыбо-мясо, то станет веселее:

То есть, кот может есть рыбу, собака «Рыбо-мясо», а кролик — морковь. Ладно, со зверьми разобрались, а как же я? Я ведь лучше собаки, и могу есть, собственно, всё. Достроим полурешётку до конца, введя вершину «еда» (мужская, 1кг):

А что эта диаграмма даёт? Фактически, мы построили некоторое «обратное дерево решений». Например, если жена, открыв холодильник, говорит, что «ну зверям есть чем закусить», я знаю, что сам с голоду точно не помру. Или, если осталась еда на кота, а сам кот уехал на дачу, то можно покормить собаку.
Но это мы разобрали случай, когда у нас есть вся информация, всё хорошо и понятно, просто «потребители» разные. Давайте теперь рассмотрим случай, когда у нас наоборот, «что делать?» — кристально понятно, но вот информации об окружении либо недостаточно, либо избыточно (с противоречиями).
Неполная информация
Представим мысленно участок леса, поскольку на полях здесь недостаточно места, чтобы его нарисовать. В лесу растут ёлки, сосны, берёзы и осины. Куда их применять, очевидно: берёзу в баню, осину в колодец, сосну на мачту, а ёлку на Новый Год. Только хочется узнать, сколько же каких деревьев в нашем лесу. И вот некий Вася идёт считать и насчитывает 20 ёлок, 10 сосен, 15 берёз и 17 осин. И всё бы ничего, но ещё 8 деревьев он записал как «пих», дескать иголки у них странные, а ещё 9 как «карельский дуб», дескать какие-то листья у них странные.
В общем, по-хорошему, данные в мусор, Васю в лес, день потерян. Но, может всё-таки, можно что-то вытащить? Мы же знаем, что ещё 8 хвойных, а 9 — точно лиственных. Значит, мы можем тоже построить полурешётку:

То есть, дополним наш изначальный ADT, который мы держали в уме
data Дерево = Ель
| Сосна
| Берёза
| Осинаещё двумя позициями: «НепонятноеХвойное», «НепонятноеЛиственное». Ну и для полноты можем добавить «НепонятноеДерево». Фактически, мы использовали что-то вроде полурешётки всевозможных подмножеств, но не совсем:«НепонятноеХвойное = Хвойное \ (Сосна и Ель)».
Эту полурешётку ещё очень удобно использовать для обновления данных. Скажем, сегодня вечером мы классифицировали каждое найденное Васей дерево по этой решётке. А наутро Вася ещё раз сходил в лес и воротился с вестью, что дерево у дороги — это не берёза, а осина. Веры ему на этот раз, конечно, нет, поэтому мы дерево у дороги перезапишем не как осину, а как «НепонятноеЛиственное» — уж листья с иголками Вася наверняка не перепутает. Дальше, конечно, сами можем сходить и уточнить.
А что же позволяет такое кодирование? Мы старались, сберегали информацию, должны и получить какую-то выгоду. И получим! Конечно, мы не можем ответить точно на вопрос «сколько же у нас ёлок?», но зато мы можем совершенно точно ответить на вопросы
а зелёным ли будет лес зимой?
а сколько надо посадить осин, чтобы точно хватило на 45 колодцев?
а хватит ли у нас ёлок для 25 празднеств, если там всё равно напьются и не отличат сосну от ели?
А этих ведь ответов не было, если бы мы просто выбросили «грязные» данные. Да, без сомнения, полная информация была бы лучше, но можем ли мы её заполучить?
То есть, полурешётки и решётки очень удобны для аппроксимации, то есть приближения дискретных данных. Они, фактически, вводят формально понятие неточного дискретного значения. Это широко используется в стат. анализаторах.
Заключение
А задача, которая послужила поводом к статье — классифицировать заголовочные файлы библиотек на интерфейсные (, ) и внутренние (../bits/*). Человеку, знакомому с законами Мерфи сразу понятно, что обязательно будет «серая зона» — когда мы что-то про заголовок знаем, но как-то неотчётливо. И вот для того, чтобы сразу, на этапе прикидок проектирования поймать эту «серую зону», втиснуть её в жёсткие рамки формализации, очень удобны решётки. То есть, когда мы видим какую-то классификацию и знаем, что тут законы Мерфи действительно работают, нужно сразу же прикинуть, а какую решётку, подобную «лесной» тут есть смысл построить?
Так что же с программистом? Конечно, надо поставить стакан с пивом!
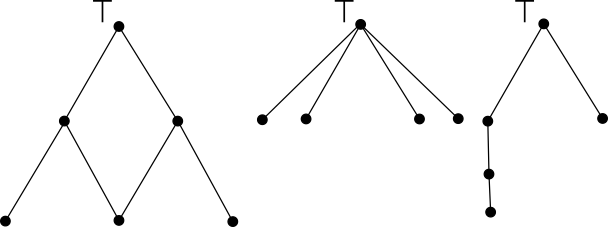
P.S.
На КДВП изображён чум, а буквы лямбда схематично обозначают оленей.
Комментарии (65)

ReadOnlySadUser
18.12.2022 23:36+1Раз уж меня впервые упомянули в статье, я теперь просто обязан её прочитать разобраться :) Хотя у меня большие сомнения, что я когда-нибудь в жизни буду применять эти знания :)

0xd34df00d
19.12.2022 00:05Вообще это всё напомнило how an optimizing compiler works — там по факту тоже строятся решётки с приближениями доступной инфы по статическому анализу кода.

vkni Автор
19.12.2022 02:19Оттуда и стырено (не из статьи, а из стат. анализа). Но, речь о том, что оно должно работать более-менее везде, где есть серые зоны. И позволяет формализовать приближения.

Refridgerator
19.12.2022 06:51+1В начале вы пишите, что в решётке определена операция ≤, но дальше этот момент не раскрывается. Например непонятно, что больше: килограмм мясо-рыбы или две морковки?

murkin-kot
19.12.2022 12:38В конце текста есть примеры с иерархиями. Для иерархии не важно, сколько килограммов в конкретном узле, потому что узел - абстрактный, то есть вмещает любое количество экземпляров (представителей вида). Абстрактная "морковь вообще" может быть одна штука, может быть десять, и может быть два кило, но общее для всех этих кучек - это морковь. То есть от параметров цвет, вес, длина, толщина и т.д. мы абстрагируемся, или забываем о них. Остаётся лишь название. Классификацию же продуктов на морковь и прочее мы отдаём столь же абстрактному классификатору, устройством которого не интересуемся. Ну и за одно нам не интересно, есть ли он в природе, потому что для нас главное - типы, и то, что в голове мы их можем выделить, а могут ли это сделать реальные классификаторы, нам безразлично. Таковы свойства абстракции, как, собственно, и всей математики.
Хотя да, отношение "больше или равно" действительно не задано для упомянутых в тексте иерархий. Оно подразумевается. Примерно задать можно так - элемент множества с более высоким уровнем абстракции находится в отношении "больше или равно" с элементом с менее высоким уровнем абстракции со стороны "больше". Если в иерархию добавить "морковь мытую" и "морковь немытую", получим, что оба этих элемента множества узлов в иерархии находятся в отношении со стороны "меньше" если вторым в отношении будет узел (элемент множества) "морковь", ну или "морковь" "больше или равна" чем "мытая морковь" (что точнее, поскольку отношение "меньше" в системе нами не задано).
В целом - текст не для тех, кто ожидает строгости. Но никто не мешает ввести строгость самостоятельно в качестве упражнения. Для остальных же строгость будет большой помехой (до поры до времени).

Refridgerator
19.12.2022 14:07+2С моим бэкграундом все иллюстрации к статье подпадают под понятие «ориентированный граф», который можно построить из отдельных узлов с определёнными для них отношениями вложения через топологическую сортировку. Соответственно и интересно, в чём разница, в чём преимущества, и можно ли отсюда извлечь для себя что-то ценное.

murkin-kot
19.12.2022 14:40Взгляд на графы через решётки - вот и вся разница.
Ценное - новый взгляд часто упрощает какие-то моменты из взгляда по старому.
Теория групп, например, подходит для множества случаев, от теории чисел до геометрии, тем самым обобщая наш взгляд на эти задачи. Решётки - частный случай общей алгебры, как и группы.
Что сказать конкретно? Да не знаю. Потому что и сам автор лишь переводит стрелки на произведение, ссылку на которое даёт в начале статьи. Видимо нужно прочитать то произведение, что бы указать вам на конкретику.
Хотя да, автор мог бы быть более щедрым на пояснения. Но он написал в конце, что статья для кого-то конкретного, а все остальные - так, довесок, поймёте - хорошо, нет - автор не будет против.

Refridgerator
19.12.2022 16:59Ну или наоборот — посмотреть на решётки через графы. Вопрос в том, в чём больше смысла? Что могут мне дать решётки из того, что не могут дать графы?

vkni Автор
19.12.2022 19:00Хотя да, автор мог бы быть более щедрым на пояснения.
Автор не настолько крут, чтобы излагать достаточно новую для него вещь в популярном ключе. Надо писать, да. Но Хабр завален спамом и политикой (в которой, азм грешен, сам принимаю участие — см историю моей кармы :-) ).

murkin-kot
19.12.2022 21:05Напишите хотя бы просто обзор той книги, где активно используются решётки. По ходу обзора станет видно, что именно решётки дают нам в контексте анализа программ. Затем это нечто можно слегка допилить своими домыслами, чем ещё более расширить понимание полезности закономерностей, выведенных для решёток.
Хотя я вполне допускаю, что автор той книги просто использовал привычную ему терминологию, не привнеся в собственно анализ ничего полезного из общей алгебры.

vkni Автор
19.12.2022 21:11Напишите хотя бы просто обзор той книги, где активно используются решётки.
Это большой и неблагодарный труд. Жизнь коротка, увы.

vkni Автор
19.12.2022 18:07ЧУМ и рисуется через DAG. При этом, он не обязательно связан, у этого DAG не обязательно есть начало и конец. У DAG для решёток такие два места обязательно есть.
То есть, это просто два представления одного и того же. Вы же изучали теорию представлений групп? Вы же знаете, что у одной и той же группы есть мало того, что бесконечное количество матричных представлений, так даже неприводимых бесконечно много.
Refridgerator
19.12.2022 18:46Не, я на информатика учился, а не на математика. Математики был стандартный курс, без вот этого всего.

vkni Автор
19.12.2022 18:58Ну сколько вы жить собираетесь? Вполне будет время добрать математические курсы.
Я, видимо, вас перепутал.

Refridgerator
19.12.2022 19:04Ну я и добираю, вот только в некоторых вещах не вижу смысла. Вот например, умножение комплексных чисел можно представить как умножение матрицы на вектор, но какой в этом смысл? Умножение комплексных чисел коммутативно, а матрицы на вектор — нет. Комплексные числа имеют одинаковые размерности, а матрицы и вектора — нет. Из комплексных чисел можно вывести гиперкомплексные, а из матриц и векторов — нет. И т.д. и т.п.

vkni Автор
19.12.2022 20:11Вот например, умножение комплексных чисел можно представить как умножение матрицы на вектор, но какой в этом смысл?
Это вам открывает возможности использовать инструкции SIMD для комплексных чисел! Кстати, поздравляю, я об этом даже и не думал.
Ну я и добираю, вот только в некоторых вещах не вижу смысла.
Отлично! Я тоже не видел в йуности смысла во всех этих алгебрах, которых нам "агрономам" преподавали.
А сейчас я понимаю, что раз понятие зубодробительно абстрактное, значит его можно применить ко всему. Ну будет оно полезно или нет — это другое дело. Но, поскольку оно абстрактное, а значит, торчит везде, как в бочке затычка, то в огромном кол-ве мест оно будет полезно.
Вы ведь знаете, что нам непосредственно в мозг "прошивали" теорию множеств в дет. саду? На яблоках? Ну и практически все "индустриальные люди" её используют повседневно. Вы можете прочитать про отличие нашего сознания от первобытного — где эта теория множеств не прошита. Ну для них нет чисел: пять яблок никак не соотносятся с пятью апельсинами.

Refridgerator
19.12.2022 20:18В SIMD матрицы ещё не завезли, хотя было бы неплохо. Переформулирую вопрос: как вывести матрицу поворота для 2D векторов, опираясь только на положения линейной алгебры, без привлечения тригонометрии или комплексных чисел?

murkin-kot
19.12.2022 20:54Для ответа вы должны подумать, как в линейной алгебре определена операция "поворот"?

Refridgerator
20.12.2022 05:09Я и сам думал, и знающих людей спрашивал, и ответа кроме как «никак» пока не получалось.

vkni Автор
20.12.2022 05:42На вскидку
линейное преобразование, сохраняющее норму вектора
(ну и что-то там надо добавить про положительно определённую матрицу, чтобы отсечь отражения)

Refridgerator
20.12.2022 05:47Ну хорошо. Вот у нас есть 3D-вектор [1,1,1], нужно провернуть его вокруг своей оси, как сверло. Давайте это ваше линейное преобразование, посмотрим, что получится.

vkni Автор
20.12.2022 08:13???
Повернуть вектор невозможно. У него же нет ориентации — это не палка с продольными метками.
Если в про поворот, главная ось которого параллельна вектору (1, 1, 1), то их бесконечно много. Но я не очень понимаю, зачем я должен мучаться и предоставлять вам матрицу такого поворота. Чем это поможет?
Вообще, у меня такое ощущение, что у вас не было двухсеместрового курса линейной алгебры. Так?

Refridgerator
20.12.2022 08:47Ну вот об этом и была речь — отталкиваясь от линейной алгебры вы приходите к решению «невозможно», хотя это очевидно возможно для каждого, кто видел дрель. Линейная алгебра была ещё в школе, и что это меняет?

vkni Автор
20.12.2022 16:29+1В данном случае вы используете неправильную модель. Если вам нужно обязательно описать объект, похожий на палку со сторонами, то один вектор для этого, очевидно, не подходит.
Ну ровно также не подходит точка для описания объекта, когда его форма критична.
Но это — мат. моделирование реального мира проходят на физике. А физику, насколько я понимаю, в РФ нормально преподают в одной школе.

Andy_U
20.12.2022 20:39Вы имели ввиду "написать матрицу вращения, которое данный вектор оставляет неизменным"?

vkni Автор
20.12.2022 21:42У нас ниже/выше трёп, по результатам которого оказалось, что ув Refridgerator хочет, чтобы модель описывала раскрашенную ракету, а не просто направление.

Andy_U
20.12.2022 22:49+1У нас ниже/выше трёп, по результатам которого оказалось, что ув Refridgerator хочет, чтобы модель описывала раскрашенную ракету, а не просто направление.
Так ортонормированный базис годится для описания любого твердого тела.

vkni Автор
20.12.2022 23:45У нас скорее программистский спор. О том, зачем нужны абстракции (ну, типа продолжения спора о том, нужна ли программисту Высшая математика).

Refridgerator
21.12.2022 05:35Не «раскрашенную ракету», а, например, сверло у дрели. На которое можно насадить лопасти и получить вентилятор. Положение лопастей будет зависеть ещё и от угла поворота сверла, и такую систему описать 3D-векторами не получится.

Refridgerator
21.12.2022 05:29Я имел ввиду, что у 3D-вектора недостаточно степеней свободы, чтобы хранить состояние вращения вокруг своей оси. А если добавить для этого дополнительную координату, как угол — то для такого 4D-вектора не получится определить матрицу вращения. Не получится даже просто его масштабировать умножением на константу.

vkni Автор
21.12.2022 05:48Ну, значит в этом случае вам надо взять другую абстракцию.
Мы же в любом случае не можем в программе закодировать цельное сверло, как оно есть — там 10E23 атомов. Это я ещё не говорю, что там кванты.
Ну, а дальше мы выбираем просто подходящую абстракцию, которая описывает то, что нам нужно и ничего более. То есть, в вашем случае сверла нужно 6 степеней свободы для положения в пространстве.

Refridgerator
21.12.2022 06:03Тут дело не в другой абстракции, а в том, что линейная алгебра ограничена в своих возможностях даже применительно к понятию «вектор». В случае сверла достаточно 4-х степеней свободы, а как его корректно описать в терминах линейной алгебры можно узнать у другого, чуть более грамотного математика (я не математик если что).

Andy_U
21.12.2022 11:32А это уже не вектор. Две таких массива даже не сложить толком (т.е. можно поэлементно, но физического смысла нет).

Andy_U
20.12.2022 20:33И еще скалярные произведение любых пар векторов? Cм. https://ru.wikipedia.org/wiki/Унитарная_матрица

vkni Автор
20.12.2022 21:40Я специально не смотрел, а изобретал из сам, по мотивам
"Я и сам думал, и знающих людей спрашивал, и ответа кроме как «никак» пока не получалось."
А так, да, через скалярное произведение правильнее.

murkin-kot
20.12.2022 12:47Из википедии:
Ве́кторное простра́нство (лине́йное пространство) — математическая структура, представляющая собой набор элементов, называемых векторами, для которых определены операции сложения друг с другом и умножения на число — скаляр
Оттуда же:
Эти операции подчинены восьми аксиомам
Итого:
Определение операции "поворот" в списке допустимых отсутствует.
Но вы можете сузить толкование математической структуры добавкой вашего определения операции "поворот" (сузить в плане уменьшения количества переходов между элементами множества посредством введения новых ограничений (аксиом)).
Любой математический инструмент опирается на набор аксиом. Линейные преобразования на то и линейны, что бы не выходить за предписанные рамки.
Или по другому - вы задались не тем вопросом. Или выбрали не тот инструмент.
Правильный подход - пояснить, зачем вам вообще понадобилось вдруг исключить тригонометрию и комплексные числа.

Refridgerator
20.12.2022 13:39Пояснить: поворот, как интерпретация умножения комплексных чисел, не постулируется, а является следствием i2=-1 без привлечения какой-либо тригонометрии. Чтобы увеличить размерность пространства с сохранением такой интерпретации достаточно в качестве компонент комплексного числа взять другие комплексные числа и не обязательно даже приводить их к кватернионному виду. С матрицей поворота такой фокус не прокатит потому что она постулируется, а не выводится.

murkin-kot
20.12.2022 16:10Интерпретация есть внематематическое действие. Математике нужны аксиомы, множества, операции. Где в этой троице интерпретации?
Поворот при возведении в квадрат i является геометрической интерпретацией. Для введения в математику такая операция требует указания перехода от геометрии к комплексным числам. Но даже представив такое отображение вы будете противоречить сами себе, ведь вы потребовали "без тригонометрии и комплексных чисел".
Задайте какую-то основу, затем задайте отображение из неё на геометрию, так получите углы, а без углов все преобразования будут лишь наборами чисел, каким-либо строгим образом не связанным с понятием "поворот", которое всегда предполагает наличие угла.

Andy_U
20.12.2022 20:36Определение операции "поворот" в списке допустимых отсутствует.
Это же линейное преобразование, матрица кoторого унитарная (ортогональная).

murkin-kot
21.12.2022 13:24Если кто-то использует молоток для забивания шурупов, это не значит, что именно так все и должны делать.

Andy_U
21.12.2022 14:15Прощу прощения, не могли бы вы уточнить, что вы подразумеваете под "шурупами", а что под "молотком"?
Пока что я вижу, что вы согласны с вашим оппонентом, что в векторных пространствах операция вращения отсутствует?

Andy_U
21.12.2022 16:20Странно, Марья Иванна... (С) анекдот.
(Может быть) определена, как умножение на унитарную матрицу. Естественно, это никакая не аксиома.

vkni Автор
19.12.2022 21:11Я не хочу на эту тему беседовать — она уводит меня от решёток.

Refridgerator
20.12.2022 05:21И не надо — это был просто пример по аналогии, где введение новых абстракций проблем не решает, а наоборот их добавляет.
Мне искренне интересно узнать, почему для некоторых людей набор файлов с отношением вложенности, явно прописанным как "#include", более естественно представить в виде абстрактной алгебраической группы с отношением «меньше или равно или вообще несравнимо». Как это поможет например выявлять циклические ссылки?

vkni Автор
20.12.2022 05:39Этот набор естественно рассматривать, как граф. И я не протестую, что это именно так. Это, кстати, просто направленный граф без каких-либо ограничений.
А вот давайте рассмотрим множество Сшных сущностей, добавляемое в пространство имён каждым из этих заголовков, S_i.h. Как вы эти множества опишете? Каким таким графом?

Refridgerator
20.12.2022 05:54Давайте тогда уже более конкретный пример, с кодом, чтобы не фантазировать на тему кто что имел ввиду.

vkni Автор
20.12.2022 08:10Если вы про то, что такое "Сшные сущности", то ну глобальные переменные, типы, объявления функций и т.д. Всё то, что вы можете поместить в заголовок. Скажем
int zz(int); extern int tau; struct A { ... }; typedef A struct A;

Refridgerator
20.12.2022 08:50Ну тут возможно граф избыточен, достаточно просто неупорядоченного списка.

vkni Автор
20.12.2022 16:38Тут не нужен граф вообще.
Понятно, что эти множества S_i.h вкладываются друг в друга, как матрёшки. А значит, там можно ввести операцию ≤. Это будет просто операция из теории множеств ⊆. Она опеределена не совсем между любыми двумя заголовочными файлами => это не линейное упорядочение, а ЧУМ.А дальше вы это соображение в каком-нибудь языке программирования можете закодировать графом, какими-то SET'ами и т.д. Можете закодировать десятком разных способов, например с помощью разниц.
Если, конечно, это вам вообще нужно кодировать. Может быть просто достаточно этой огрублённой информации, чтобы понять какой-же именно S_i.h вам нужен.

Refridgerator
20.12.2022 16:44Можно ли решить эту задачу без знания ЧУМ? Я решил много лет назад, значит, можно. Значит, не все абстракции одинаково полезны. Возможно, некоторые из них даже вредны.

vkni Автор
20.12.2022 17:00Какую задачу? Задачи разные, о моей вы почти ничего не знаете, кстати.
Да, очевидно, что абстракции нужны под задачу, а не просто так.

vkni Автор
20.12.2022 18:34Конкретно решётки массово используются для подподзадачи компилирования, для анализа кода в middle-end, внутри оптимизаторов. Если вы пишете компилятор без оптимизаций или они относительно простые, то можете написать без формализации и без решёток.
Это же просто абстракция, которая в определённых ситуациях позволяет выбросить ненужные детали, упростив картину мира => сделав её проще для осмысления и разных действий поверх.

Andy_U
20.12.2022 20:45Так вы сами в статье отошли, все примеры - это деревья.
P.S. Я ожидал что-то типа MRO в питоне: https://data-flair.training/blogs/python-multiple-inheritance/

Deosis
20.12.2022 08:29Каждый столбец в матрице трансформации показывает, в какой вектор перейдет соответствующий базисный вектор при этой трансформации.

vkni Автор
20.12.2022 16:36Например непонятно, что больше: килограмм мясо-рыбы или две морковки?
Про килограммы не упоминалось => их нет, забудьте. В другом примере, возможно, они будут, но тут их нет, нет, нет.
ЧУМ — частично-упорядоченное множество на то и частично, что не между всеми объектами есть сравнение ≤. Вы же наверняка у папы спрашивали в детстве, какая машина круче? Я своим детям рассказываю про Феррари и КРАЗ-самосвал. И показываю, что их нельзя упорядочить: в одних задачах лучше Феррари, а в других — КРАЗ. То есть, там нет ≤.
Аналогично, например, кто круче — первая красавица класса или самый крутой парень? Они не сравнимы: женская иерарахия и мужская независимы.


vadimr
Почему третий пример (шестиугольник с двумя диагоналями) не является решёткой?
vkni Автор
Потому, что я несколько напортачил с определением (исправил). Нужно наличие точной верхней и нижней граней.
gchebanov
Для будущих читателей поясню: например у пары детей верхнего (максимального) элемента есть точная верхняя грань, но нет точной нижней - нижними гранями являются минимум и два его отца, но в этом трех элементном множестве нет наибольшего элемента.
gchebanov
Странный факт - в индексе поисковиков всего одно вхождение по запросам "для будущих читателей поясню" и "для будущих читателей поясняю", наверное я косноязычно выразился.
vkni Автор
Нет, наверное вы просто не нейросеть! :-)
qyix7z
Инь Фу Во кивнул.
– Я ввёл его в Гугле, – продолжал Сисадмин, – и убедился, что в Сети такого сочетания нет.
– Теперь есть.
vkni Автор
Реально статья написана ради последних двух разделов, которые обещаны паре людей. Просто если я начал бы с конца, кмк, были бы замечания.