Нетранзитивными игральными костями я заинтересовался, когда увидел задачу Нетранзитивные кубики на Элементах. Приведенное на сайте решение меня абсолютно не удовлетворило (собственно это и решением назвать нельзя - автор просто выдал готовый ответ). Послесловие оказалось не лучше, что только подстегнуло интерес к задаче.

Остались вопросы. Можно ли построить набор кубиков "с нуля"? Как построить набор костей с другим количеством граней? Будут ли там решения с равными вероятностями выигрыша? Я попытался найти общий алгоритм со следующими условиями:

1. Алгоритм должен работать для любого количества костей с любым количеством граней (равным для всех костей в наборе).

2. Все кости выигрывают у своего соседа в наборе с равной вероятностью.

3. Алгоритм должен создавать набор для любой заданной вероятности выигрыша.

Для демонстрации идеи возьмем следующий нетранзитивный набор из 4-х кубиков:

A:  1,  2, 16, 17, 18, 19
B:  3,  4,  5, 20, 21, 22
C:  6,  7,  8,  9, 23, 24
D: 10, 11, 12, 13, 14, 15

В этом наборе A < B < C < D < A с вероятностью 24/36. Представим его в следующем виде:

AABBBCCCCDDDDDDAAAABBBCC

Здесь порядковый номер символа равен числу на соответствующей кости. Теперь можно абстрагироваться от конкретных чисел и сравнивать расположение символов относительно друг друга. Например количество пар A и B, в которых A стоит слева от B (т.е. A < B) равно 24. Эти пары соответствуют элементарным исходам бросков костей A и B, в которых выигрывает кубик B, что и дает вероятность выигрыша 24/36.

Итак, чтобы построить нетранзитивный набор костей, нужно найти такую перестановку символов, в которой количество пар "X < Y" одинаково для всех соседних в наборе костей и соответствует искомой вероятности. Как это сделать?

Перестановку можно получить из таблиц выигрышей. Для рассмотренного выше набора они выглядят так:

Закрашенные ячейки соответствуют исходам, в которых кубик проигрывает соседу слева (назовем их "проигрышными ячейками"). Числа под таблицей показывают расположение в перестановке символа кубика относительно символов его соседа слева. Например из таблицы AB следует, что первый, второй и третий символы B стоят после второго символа A, а четвертый, пятый и шестой B - после шестого A. Чтобы получить перестановку для нетранзитивного набора, возьмем следующую перестановку:

AAAAAABBBBBBCCCCCCDDDDDD

и будем последовательно сдвигать символы в соответствии с таблицами выигрышей:

AABBBAAAABBBCCCCCCDDDDDD
AABBBCCCCAAAABBBCCDDDDDD
AABBBCCCCDDDDDDAAAABBBCC

Замечу, что вообще из таблицы выигрышей нельзя однозначно получить перестановку. Например, двум перестановкам:

AADC DB CBBBCCDDAD CAA BABCD
AADC BD CBBBCCDDAD AAC BABCD

соответствуют одни и те же таблицы выигрышей. Но нам лишь важно, что в обоих наборах будет одна и та же вероятность выигрыша.

Теперь самое сложное - нужно построить таблицы выигрышей, соответствующие искомому нетранзитивному набору костей. Набор таких таблиц должен удовлетворять некоторым условиям, которые мы сейчас сформулируем:

Выберем на каждой игральной кости по одной гране. Этим граням будут соответствовать ячейки в таблицах выигрышей (по одной в каждой таблице) такие, что номер столбца ячейки в одной таблице будет равен номеру строки ячейки в следующей таблице. Например, для рассмотренного выше набора 4-х кубиков это выглядит так:

Очевидно, что в любом таком наборе ячейки не могут быть все выигрышными или все проигрышными.

Далее рассмотрим наборы ячеек, состоящие только из ячеек на главной диагонали таблицы - в каждом таком наборе у всех ячеек будут совпадать номера строк и столбцов. Так как все ячейки в наборе не могут быть выигрышными, то для каждой ячейки на главной диагонали в наборе таблиц выигрышей должна быть хотя бы одна таблица, в которой эта ячейка будет проигрышной (и хотя бы одна таблица, в которой эта ячейка будет выигрышной).

Второе условие также дает ограничение на максимальную вероятность выигрыша. Для костей с четным количеством граней минимальная площадь проигрышной области будет у прямоугольника с одной из двух центральных ячеек главной диагонали в правом верхнем углу. Для костей с нечетным количеством граней это будет квадрат с центральной ячейкой в правом верхнем углу. Т.е. максимальная вероятность выигрыша равна для костей с четным количеством граней:

и для костей с нечетным количеством граней:

где s - количество граней.

Теперь на нескольких примерах покажем как построить таблицы выигрышей, удовлетворяющие этим условиям:

Начнем с нашего примера из 4-х кубиков с вероятностью выигрыша 24/36. Область проигрышных ячеек во всех таблицах будет иметь форму прямоугольника. В 1-й таблице высота этого прямоугольника будет равна высоте таблицы. В каждой следующей таблице высота прямоугольника будет убывать так, чтобы где и - высота и ширина прямоугольника в i-й таблице:

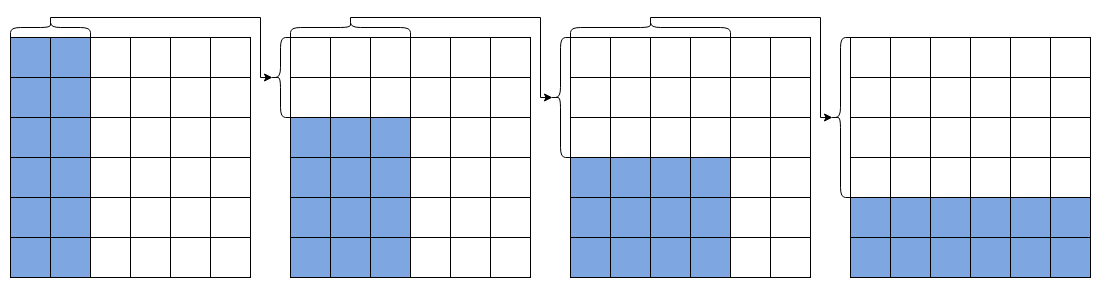
В этом примере хорошо видно, что все наборы ячеек удовлетворяют первому условию.

Добавим в искомый набор несколько кубиков. Тогда в наборе таблиц выше нужно продублировать любую таблицу до нужного количества кубиков, соблюдая порядок убывания высоты прямоугольников с проигрышными ячейками. Например, для набора из 6 кубиков таблицы выигрышей могут выглядеть так:

Следующий пример - 4 кубика с вероятностью 21/36. Также разместим проигрышные ячейки в прямоугольные области убывающей высоты (на рисунке закрашены синим). Оставшиеся проигрышные ячейки (закрашены зеленым), не вошедшие в основную прямоугольную область, разместим так: во всех таблицах, кроме последней - столбцом справа от прямоугольника, в последней таблице - в несколько столбцов над прямоугольником:

Уберем из последнего набора один кубик. При текущем способе построения таблиц выигрышей мы не можем получить таблицу, в которой область проигрышных ячеек покрывает правую нижнюю ячейку таблицы. Исправим это. Разместим в 1-й таблице проигрышные ячейки в две прямоугольные области: высота первой так же равна высоте таблицы, а ширина второй (закрашена фиолетовым) дополняет ширину первой до ширины таблицы. Оставшиеся ячейки разместим в столбец справа от первой области и над второй:

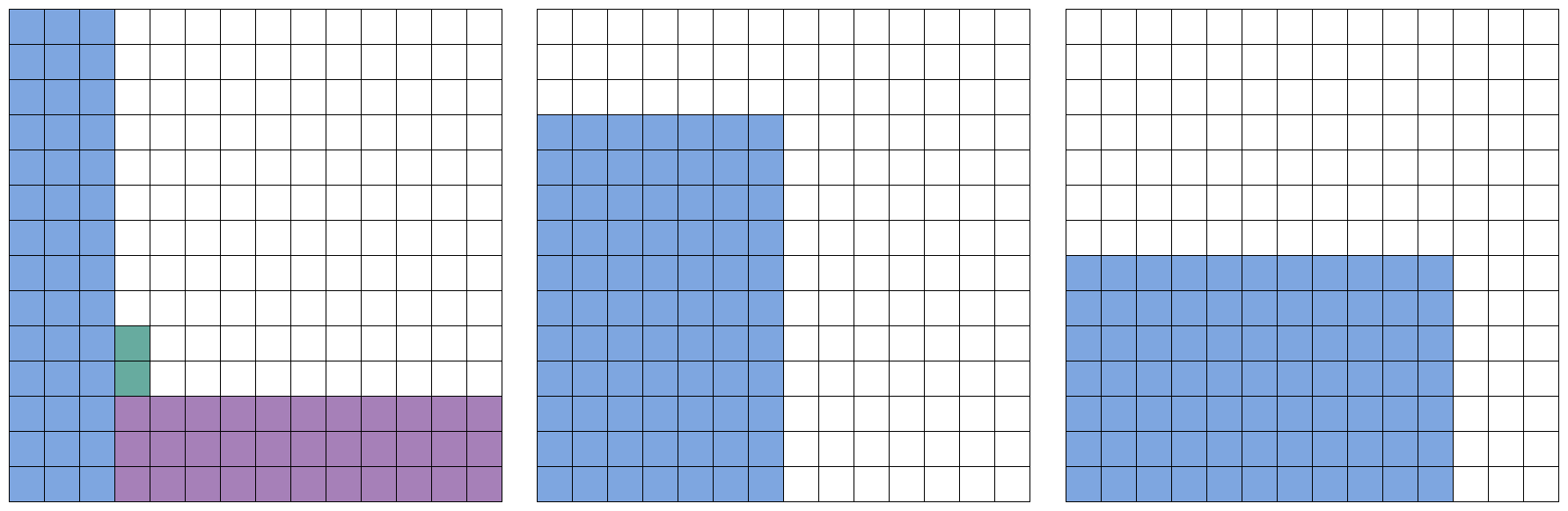
Для наборов с большим количеством граней и малым количеством костей высота второго прямоугольника в 1-й таблице может быть несколько строк, но не больше ширины первого прямоугольника. Этот параметр нужно найти перебором - чтобы ширина прямоугольника в последней таблице равнялась ширине таблицы за вычетом высоты второго прямоугольника в 1-й таблице. Например, для набора из трех 14-гранников с вероятностью 119/196 таблицы выигрышей выглядят так:

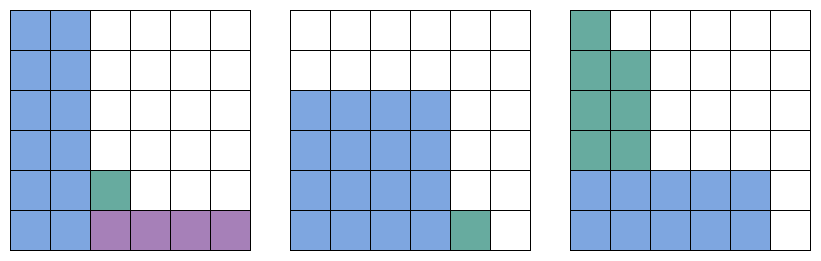
Наконец рассмотрим пример из трех кубиков с вероятностью 19/36. В 1-й таблице столбец проигрышных ячеек, не вошедших в основной прямоугольник, не может быть выше главной диагонали. На рисунке ниже красным показаны 3 набора ячеек, в каждом из которых все ячейки являются проигрышными, что противоречит первому условию:

В этом случае следует сразу начать с размещения в 1-й таблице проигрышных ячеек в два прямоугольника:

Если описанным выше способом не удается построить набор таблиц выигрышей - значит для заданного количества костей и граней искомая вероятность выигрыша недостижима. Например, из трех кубиков нельзя построить нетранзитивный набор с вероятностью выигрыша больше, чем 21/36.

Ссылка на реализацию алгоритма.