Ключевые элементы машинного обучения и скрытых пространств

Эта статья послужит введением в представление (embedding), подобие (similarity) и кластеризацию (clustering).

Знать эти ключевые понятия машинного обучения нужно, чтобы понять, что такое скрытое пространство.

• Под представлением понимается представление реального мира в виде данных. Только после представления мы сможем анализировать и использовать в приложениях объекты и явления реального мира.
• Подобие определяет степень сходства между представлениями реального мира и позволяет, например, рекомендовать тот или иной товар.
• Кластеризация позволяет объединить представления реального мира в группы, например, чтобы найти книги по заданной тематике.

За подробностями приглашаем под кат.

1.1 Представление (embedding)

Компьютеры могут представлять и анализировать происходящее. Примером такого представления может быть текст книги, который можно прочесть, и изображения, которые можно передать по сети.

Компьютер понимает только числа. Поэтому мы должны любые данные представлять в цифровом виде, то есть оцифровать. Что и как мы хотим представить? Поясню это на примере книги. Допустим, мы снимаем её страницы цифровой камерой. Матрица камеры состоит их множества крошечных сенсоров. Каждый сенсор определяет цвет, который он видит, и представляет его в цифровом виде.

Рисунок 1.1 — Процесс оцифровки изображения.

Для представления книги понадобится множество чисел, а для оцифровки буквы «G» их потребуется 5x5=25. Для оцифровки предложения из 48 символов понадобится 25x48=1200 чисел. Страница в 28 строк требует 1200x28=33600 чисел, а вся книга из 250 страниц потребует 33600x250=8400000 чисел, что уже весьма немало!

Когда мы делаем снимок, мы спрашиваем не только о содержании книги. Мы спрашиваем, как выглядит наша книга, в каком она состоянии, как она освещена, и насколько она удалена от объектива камеры. Но в случае книги не нужны все эти подробности. Мы можем уменьшить число цифр, отказавшись от некоторых деталей, а спросить только о содержании книги. Цифры и латинские буквы часто представляют в формате ASCII. Мы представляет их цифрами от 48 до 122, и компьютер знает, что 48 — это ноль, а 71 — это заглавная «G». Формат ASCII кодирует каждый символ одним числом, поэтому то же предложение будут представлять всего 1x48=48 чисел, страницу 48x28=1344 чисел, а всю книгу 1344x250=336000 чисел.

Рисунок 1.2 — Предложение из книги, представленное в формате ASCII.

Рисунок 1.3 — Таблица кодирования латинских букв и цифр в формате ASCII

Но книгу можно представить и меньшим набором чисел. Если, например, для нас важно не содержание, а жанр книги, мы может просто задать его, например, как «фэнтези», «биография», «ужасы», «документалистика». Для примера увеличим число возможных жанров до 256. Тогда мы можем присвоить книге значение «1» (истина), если жанр совпадает с заданным, и «0» (ложь), если это не так. Теперь книга любого размера может быть представлена всего 256 битами или 32 числами (на число приходится 8 бит)! В этом суть компромисса между количеством представленной информации и объёмом данных.

Рисунок 1.4 — Представление книги значением жанра. 1 (истина) означает, что книга относится к данному жанру, а 0 (ложь) — что не относится.

Представление должно быть разным для разных прикладных задач. Жанры удобнее, когда нужно порекомендовать книгу, похожую на ту, которая понравилась читателю. Чтобы прочесть выбранную книгу, нам уже нужно её содержание, а для просмотра обложки — изображение.

Чтобы хорошо выполнить представление, мы должны знать, какие данные нужны приложению и как оцифровать их. Как и в нашем примере с книгами, разные части приложения требуют разных представлений.

1.2 Подобие (similarity). Векторизация (vectorization)

Цель подобия — найти схожие представления. Примером может быть использование подобия для рекомендации читателю книг, похожих на прочитанные им ранее.

Что же такое подобие? Подобие основано на представлениях (также называемых измерениями, образцами или точками), которые можно поместить в систему координат. Мы будем также называть систему координат пространством координат (или просто пространством, для краткости). При помещении представления в пространство (dimentional space) оно становится точкой (point). Ниже приведены точки для четырёх книг, помещённых в двухмерную систему координат.

Рисунок 1.5 — Представления 4 книг в двухмерной системе координат на основании их художественности и биографичности.

Чем ближе друг к другу точки в пространстве, тем больше схожи между собой книги. Две документальных книги (точки A и B) более похожи друг на друга, чем документальная и художественная (точки A и C). Подобие зависит от расстояния между точками. Как показано на рисунке 1.6, L1 < L2. A и B схожи больше, чем A и C.

Рисунок 1.6 — Расстояние A-B (то есть, L1) и A-C (то есть L2). A и B схожи больше, чем A и C. Иначе говоря, L1 < L2.

Векторизация точек позволяет узнать расстояние между ними, а значит, и их подобие. Для векторизации требуются только точки, исходящие из (0,0). Например, точки (2,3) — это вектор [2, 3].

Рисунок 1.7 — Точки можно преобразовать в векторы с начальной координатой (0, 0)

Расстояние — это длина вектора, проходящего между двумя точками, называемая евклидовым расстоянием. Для нахождения вектора между двумя точками достаточно произвести вычитание их векторов.

Рисунок 1.8 — Евклидово подобие — расстояние между точками

Выражение 1.1 — Формула для расчёта евклидова подобия

В Python для расчёта евклидова подобия создают с помощью библиотеки Numpy, два вектора, выполняют их вычитание и находят их норму.

import numpy
import math

book_A = numpy.array([2, 3])
book_B = numpy.array([4, 1])

book_A_B = book_A - book_B

# ---- Easy Solution ----
euclidean_dist_easy = numpy.linalg.norm(book_A_B)

# ---- Manuel Solution ----
# Sum together all distances squared (pythagoras)
sum_of_squared_distances = numpy.dot(book_A_B, book_A_B)
# Find distance
euclidean_dist_manuel = math.sqrt(sum_of_squared_distances)

Код 1.1 — Расчёт евклидова подобия для двух книг с помощью выражения 1.1

Подобие также определяется через коэффициент Отиаи. В этом случае рассматривается угол между векторами, а не расстояние между их концами. Идея метода заключается в том, что соотношение концептуальных свойств важнее их приоритета. В книге А больше внимания уделяется вымыслу, а в книге B — жизнеописанию героя. Их концептуальные свойства значительно отличаются, даже если они близки друг к другу в евклидовом пространстве.

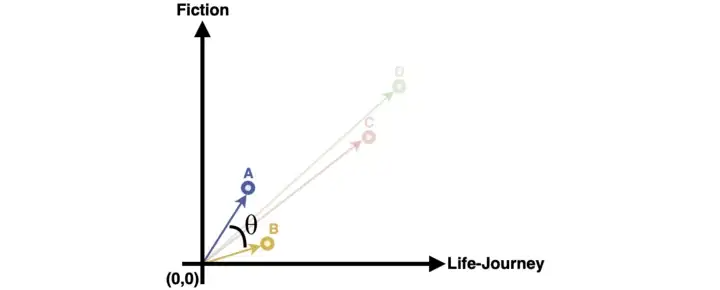
Рисунок 1.9 — Коэффициент Отиаи определяет угол между векторами

Выражение 1.2 — Формула для расчёта коэффициента Отиаи

Коэффициент Отиаи рассчитывают в Python после создания двух векторов с помощью Numpy и нахождения косинуса угла между ними с помощью Scipy.

from scipy import spatial
import math

# ---- Easy Solution ----
cosine_dist_easy = spatial.distance.cosine(book_A, book_B)

# ---- Manuel Solution ----
# Dot product between vectors
product_AB = numpy.dot(book_A, book_B)
# Length of vectors
book_A_length = numpy.linalg.norm(book_A,2)
book_B_length = numpy.linalg.norm(book_B,2)
# Similarity measures by cosine distance
cosine_dist_manuel = 1 - (product_AB / (book_A_length * book_B_length))

Код 1.2 — Расчёт коэффициента Отиаи для двух книг посредством выражения 1.2

Мы можем использовать как евклидово подобие, так и коэффициент Отиаи одновременно. Они ведут себя по-разному, и выбор между ними делает разработчик каждого конкретного приложения.

1.3 Кластеризация (clustering)

Кластеризация — метод, который позволяет группировать данные. Примером может служить рекомендация новых книг на основе групп жанров, которые мы любим читать. Очевидно, что группа включает похожие объекты и становится тем более сжатой, чем ближе расположены точки, представляющие её объекты. Задача — определить, какие точки наиболее схожи между собой, и понять, как объединить их в соответствующее количество групп. Методы кластеризации используют формулы подобия для оценки подобия между точками. На рисунке ниже создаётся две группы. При этом используется евклидово подобие точек и объединяем самые близкие из них. Кластерный анализ двух групп показывает, что в основном читаются школьные учебники и фэнтези. При этом не учитывается, любим ли мы читать учебники или читаем их лишь по мере необходимости.

Рисунок 1.10 — Две группы, определённые по близости точек: учебники (school books) и фэнтези (fantasy).

При этом число групп — это гиперпараметр. Иными словами, число групп выбирает не компьютер, а человек, и он делает это заранее. Выбор уместного числа кластеров (они же — группы) чрезвычайно важен. Принцип выбора числа кластеров показан на Рис. 1.11. Здесь данные анализируются с одним, двумя и четырьмя кластерами, что показывает влияние переменного параметра.

Рисунок 1.11 — Данные объединяются в 1, 2 или 4 кластера. 1 и 4 кластера не дают нам никакой новой информации, а 2 кластера показывают, какие книги мы прочли.

Выбор одного кластера говорит лишь о том, что нам нравятся книги. Едва ли, это полезно при создании приложения для анализа предпочтений читателей. Четыре кластера показывают нам, что нам нравятся книги A, B, C и D, но это не позволяет дать читателю практически никаких рекомендаций. Два кластера больше подходят для этого сценария, так как мы узнаём, что больше всего читаем учебники и фэнтези. Не бывает идеального числа кластеров на все случаи жизни. Что если бы мы прочитали больше книг, как в примере ниже? Подошли бы нам тогда две или четыре группы?

Рисунок 1.12 — Четыре кластера, которые были избыточны для предыдущего примера, дают нам ценную информацию в новом примере. Объединение в 4 кластера — учебники (school books), фэнтези (fantasy), биографии (biography) и фантастические рассказы (short story) позволяет лучше понять набор данных. Таким образом, идеального числа групп нет — всё зависит от предпочтений.

Распространённые методы кластеризации — кластеризация k-средних (k-means clustering)¹ и иерархическая кластеризация (hierarchical clustering)². При кластеризации k-средних, мы находим число кластеров (k), как мы делали это в примерах выше. При иерархической кластеризации мы определяем пороговое значение (threshold) и с его помощью определяем, насколько должны отличаться друг от друга кластеры. Иерархическая кластеризация, как правило, выполняется либо путем объединения ближайших точек во всё более крупные кластеры (снизу вверх), либо путем создания одного кластера и разбиения его на части, пока они не станут достаточно различимыми (сверху вниз).

Рисунок 1.13 — (Слева) Точки в системе координат. (Справа) Ближайшие точки объединяются в кластер, который, в свою очередь, сводится к одной точке для дальнейшей группировки. Этот процесс повторяется, пока расстояние между точками не преодолеет заданное пороговое значение (threshold).

Есть два подхода к кластеризации. Мы можем посмотреть, какие группы есть в существующих данных, а можем определить, к каким группам принадлежат новые точки. Первый способ подходит, если нужно разбить все книги на группы и пометить каждую из них жанром. После этого мы можем отнести новую книгу к одному из жанров вторым способом. Для этого нужно понять, к какой группе ближе всего новая точка. Определение группы для новых точек — основа их классификации. При этом оценка групп проведена на основании существующих данных.

Рисунок 1.14 — Отнесение новой точки к одной из групп зависит от того, к какой группе она ближе всего

В оставшейся части статьи подробно описывается кластеризация k-средних и её применение. Иерархическая кластеризация подробнее описана в другой статье.

1.4 Кластеризация k-средних

При кластеризации k-средних под «k» мы понимаем число кластеров. k=2 означает, что в данных нужно найти 2 кластера, а k=4 означает, что в них нужно найти 4 кластера. Слово «среднее» означает, что каждый кластер определяется средним значением для своей группы, то есть, точкой, которая условно находится в центре группы.

Кластер представляет часть данных. Для этого в имеющееся пространство добавляется новая точка. Теперь эта точка будет представлять эту часть данных.

Рисунок 1.15 — Добавление в пространство новых точек данных, которые представляют части данных

Цель метода k-средних — найти наиболее точное расположение каждого кластера. В реальности всё не так просто, как в примере выше, где точка кластера находится в геометрическом центре этого кластера. На самом деле у нас нет кругов, есть только точки. Код 1.3 находит точки, показанные на Рисунке 1.16, в Python. Он приводится как пример применения метода k-среднего.

Рисунок 1.16 — Группы не представлены цветами и кругами. У нас есть только бесцветные точки данных в системе координат (с точки зрения человека) или только таблица значений (с точки зрения компьютера).

# -------------- Define Measurements --------------
# Vector = [Life-Jouney, Fiction]
vec_a = [2, 3]
vec_b = [3, 1]
vec_c = [7, 5]
vec_d = [8, 7]
vec_e = [3, 8]
vec_f = [4, 9]
vec_g = [9, 2]
vec_h = [10, 1.8]
data_points = [vec_a, vec_b, vec_c, vec_d, vec_e, vec_f, vec_g, vec_h]

Код 1.3 — Определение точек данных из таблицы значений на Рисунке 1.16

Первый шаг к нахождению k-кластеров — случайное расположение k-точек в пространстве. Использование случайных точек может показаться нелогичным, ведь почему бы не разместить их на равном расстоянии друг от друга в пространстве. Дело в том, что все данные выглядят по-разному, что часто приводит к тому, что равноудалённые точки не попадают в центр реальной группы. Реальные группы — это те группы, которые мы хотели бы найти в своих данных, если бы всё шло идеально. Кластеризация k-средних не гарантирует нам нахождение наилучших возможных кластеров. Она лишь гарантирует нахождение наиболее подходящих кластеров в местах расположения точек. Случайные точки не гарантируют, что представление окажется хорошим. Однако высока вероятность того, что случайное расположение точек в какой-то точке даст хороший результат при многократном повторении этой операции. Использование равноудалённых точек будет либо всё время генерировать одни и те же кластеры, либо создаст вычислительные трудности при систематических расчётах.

Рисунок 1.17 — Разные положения начальных точек приводят к разным результатам при кластеризации

Итак, мы размещаем в пространстве случайные точки. У нас нет причин помещать их за пределами экстремумов существующих данных, поэтому мы помещаем их где-то в диапазоне имеющихся данных.

Рисунок 1.18 — Случайные точки кластера генерируются в пределах диапазона существующих точек

import random
import numpy

# Define range for data_points
x_coor = [data_point[0] for data_point in data_points]
range_x = (min(x_coor), max(x_coor))
y_coor = [data_point[1] for data_point in data_points]
range_y = (min(y_coor), max(y_coor))
print(f"range X: {range_x}")
print(f"range Y: {range_y}")

# Create random start position for clusters
ranges = [range_x, range_y]
n_clusters = 2
n_dimensions = len(ranges)

# Between 0 and 1
random_cluster_points = numpy.random.rand(n_dimensions, n_clusters)
for index, cluster_point in enumerate(random_cluster_points):
    range_diff = ranges[index][1] - ranges[index][0]
    # Scale value to that of the dimension[i]'s variance and shift it to its range
    random_cluster_points[index] = cluster_point*range_diff + ranges[index][0]

print(f"Clusters: {clusters}")

Код 1.4 — Генерация случайных начальных точек n-кластеров. При генерации точек в диапазоне данных применяется принцип, показанный на рисунке 1.18.

Следующий шаг — распределение начальных точек по кластерам. Каждая точка принадлежит тому кластеру, который лучше всего её представляет. C точки зрения эвристики подобия наилучшим представлением точки будет ближайший к ней кластер. Здесь мы используем евклидово подобие.

Рисунок 1.19 — Определение кластеров для каждой точки по кратчайшему расстоянию точка-кластер. Эвристически этот подход основан на евклидовом расстоянии.

import numpy

# Create Container for mapping data points to cluster
cluster_data_points = [[] for _ in clusters]

# Distribute data points between clusters
for data_point in data_points:
    # Calculate Distance to each cluster
    distance_to_clusters = [dist_func(cluster, numpy.transpose(data_point)) for cluster in clusters]
    # Get index of closest cluster
    closest_cluster_index = distance_to_clusters.index(min(distance_to_clusters))
    # Add data point to the closest cluster
    cluster_data_points[closest_cluster_index] += [data_point]

Код 1.5 — Расчёт ближайшего кластера для каждой точки данных.

Следующей задачей после распределения точек данных при кластеризации k-средних является нахождение самих «средних». Под «средним» понимается среднее значение точек данных, которые представляет кластер. После распределения точки кластеров, скорее всего, не являются средними значениями, так как они представляют только самые близкие точки данных. Поэтому необходимо переместить каждый кластер так, чтобы он стал средним значением всех своих точек данных.

Рисунок 1.20 — Каждый кластер обновляется до «среднего» значения ближайших к него точек данных.

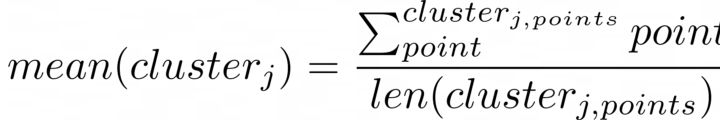
Выражение 1.3 — Формула для расчёта «среднего» значения кластера j по ближайшим к негу точкам.

import numpy

#calculate the mean for all clusters
cluster_mean = [numpy.mean(cluster_data_points, axis=0) for cluster_data_points in clusters_data_points]

Код 1.5 — Перерасчёт положения каждого кластера по среднему ближайших точек данных. Для расчёта среднего значения одного кластера используется выражение 1.3.

В новом положении кластер может оказаться ближе к другим точкам данных. Перерасчёт распределения по кластерам необходим для того, чтобы каждый кластер представлял точки данных корректно.

Рисунок 1.21 — Перераспределение точек по кластерам и перемещение кластеров в новые средние значения.

# Calculate new start position in N iterations
while True
    # Split data_points between clusters
    clusters_data_points = split_data_points_between_clusters(clusters, data_points, Similarity.Euclidean)
    # Calculate mean of each vector set as the the cluster positions
    new_clusters = calc_mean_clusters(clusters_data_points)
    #Break if clusters have not moved
    if clusters == new_clusters:
        break
    clusters = new_clusters

# Print final cluster positions
print(f"Clusters: {clusters}")

Код 1.5 — Полную реализацию с указанием всех используемых функций можно найти в соответствующем разделе репозитория

Кластеризация k-средних итеративна. Идеально расположить кластеры при одном расчёте невозможно. Нужно провести множество последовательных расчётов, и каждый из них будет приближать нас к реальному расположению кластеров. Итеративный процесс продолжается пока кластеры не перестанут двигаться или пока не будет достигнуто пороговое значение. Пороговое значение гарантирует, что процесс не будет продолжаться бесконечно.

Новые алгоритмы кластеризации создавать легко. Достаточно поменять эвристику (например, с евклидова подобия на коэффициент Отиаи) или способ представления кластером группы точек (например, медоиды вместо средних).

Для простоты SKLearn реализует надёжный метод кластеризации k-средних

from sklearn import cluster

# ---------- K-Mean clustering simplified ----------
clusters = cluster.KMeans(n_clusters=n_clusters).fit(data_points).cluster_centers_
print(clusters)

Код 1.6 — Sk-learn имеет собственную реализацию кластеризации k-средних, которая работает лучше и быстрее метода из первой главы статьи.

1.5 Заключение

Мы подошли к концу первой главы и познакомились с такими понятиями, как представление и кластеризация.

В первом разделе описывалось представление реального мира в виртуальном. Мы разобрались, почему правильная постановка вопроса может иметь решающее значение для приложения. Некоторые приложения даже требуют нескольких представлений одного и того же объекта реального мира (например, книги). Задача состоит в том, чтобы определить, какие именно представления лучше всего подходят для задач нашего приложения.

Во втором разделе говорилось о подобии между двумя объектами и его расчёте по расстоянию между точками. Для этого есть несколько способов (в частности, евклидово расстояние и коэффициент Отиаи). Каждый способ приводит к разному поведению приложения. Выбор способа, который обеспечивает правильное поведение приложения, чрезвычайно важен. Подобие можно использовать, например, для рекомендации книг, похожих на те, которые понравились читателю.

Последний раздел посвящен кластеризации. В нём показано, что подобные точки часто группируются вместе, и такие группы представляют собой базовые структуры. Книги образуют естественные группы по жанрам или тематикам (например, научная фантастика или биографическая литература). Поиск опдходящего количества групп имеет критическое значение. Как слишком малое, так и слишком большое количество групп даёт бесполезную информацию.

Благодарю вас за чтение этой книги о скрытом пространстве! Нам гораздо проще учиться, когда мы делимся своими мыслями с другими. Поэтому, пожалуйста, оставляйте свои комментарии, будь то вопросы, идеи или, может быть, контраргументы. Любые предложения и новые идеи приветствуются!

• Профессия Data Scientist (24 месяца)
• Профессия Fullstack-разработчик на Python (16 месяцев)