21.02.2023 06:43
PatientZero 5 7900 Источник
image

В первой части поста мы начали реализацию с нуля GPT всего в 60 строках numpy.

Во завершающей части мы загрузим в нашу реализацию опубликованные OpenAI веса обученной модели GPT-2 и сгенерируем текст.

Архитектура GPT


Архитектура GPT соответствует архитектуре трансформера:


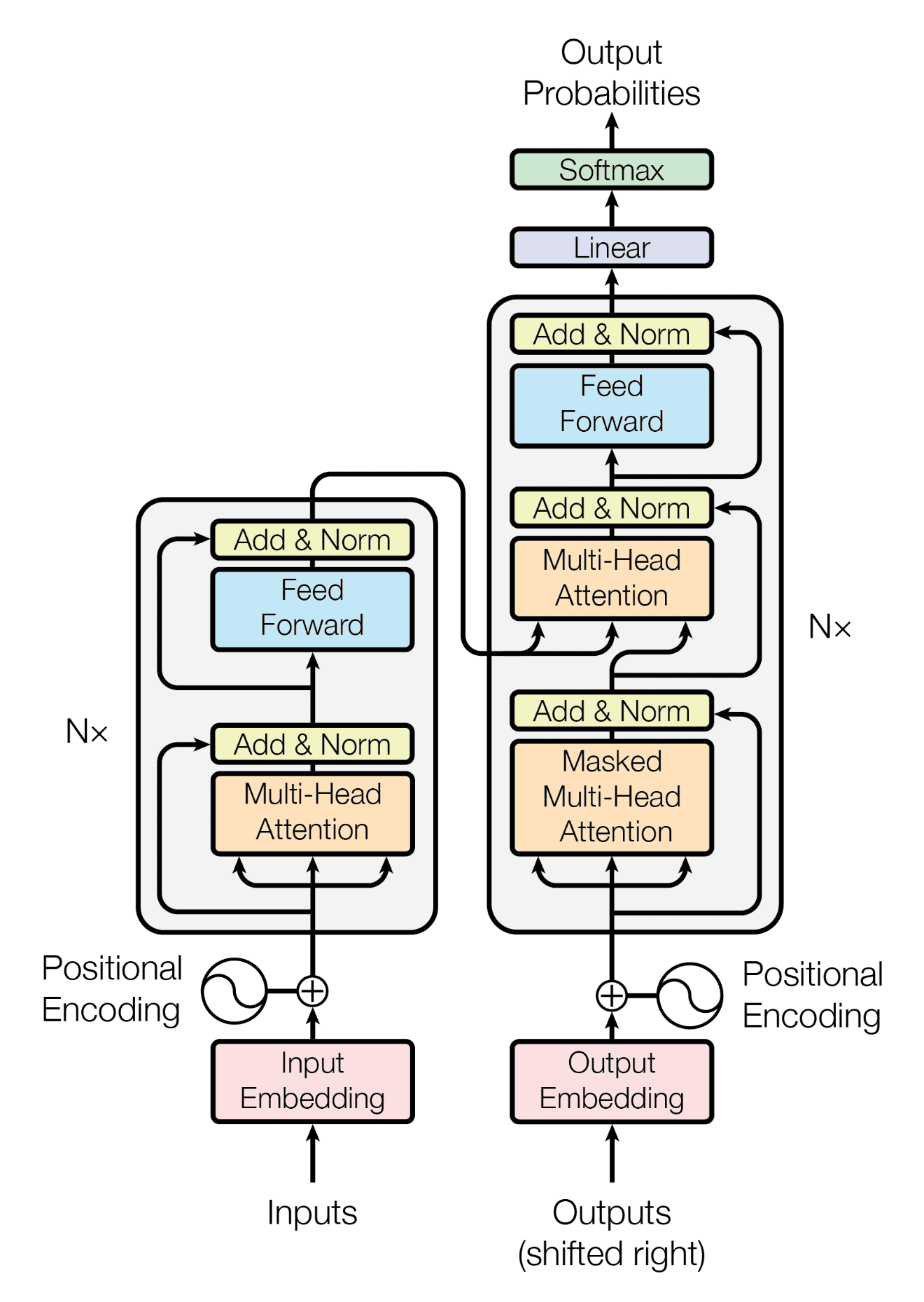
Рисунок 1 из Attention is All You Need

Но использует только стек декодера (правую часть схемы):


Архитектура GPT

Обратите внимание, что слой «перекрёстного внимания» посередине тоже убран, потому что мы избавились от кодировщика.

Если не вдаваться в подробности, архитектура GPT состоит из трёх частей:

  • Текстовые + позиционные эмбеддинги
  • Стек декодера трансформера
  • Этап проецирования на вокабулярий

В коде это выглядит так:

def gpt2(inputs, wte, wpe, blocks, ln_f, n_head):  # [n_seq] -> [n_seq, n_vocab]
    # эмбеддинги токенов + позиционные эмбеддинги
    x = wte[inputs] + wpe[range(len(inputs))]  # [n_seq] -> [n_seq, n_embd]

    # прямой проход через блоки трансформера n_layer
    for block in blocks:
        x = transformer_block(x, **block, n_head=n_head)  # [n_seq, n_embd] -> [n_seq, n_embd]

    # проецирование на вокабулярий
    x = layer_norm(x, **ln_f)  # [n_seq, n_embd] -> [n_seq, n_embd]
    return x @ wte.T  # [n_seq, n_embd] -> [n_seq, n_vocab]

Давайте рассмотрим каждую из этих трёх частей подробнее.

Эмбеддинги


Эмбеддинги токенов


Сами по себе ID токенов являются не очень хорошим форматом для нейросети. Например, относительные величины ID токенов ошибочно передают информацию (например, если в нашем вокабулярии Apple = 5 и Table = 10, то подразумевается, что 2 * Table = Apple). Во-вторых, одно число не обладает особой многомерностью для работы с ним нейросети.

Чтобы устранить эти ограничения, мы воспользуемся словами-векторами, в частности, при помощи обученной матрицы эмбеддингов:

wte[inputs] # [n_seq] -> [n_seq, n_embd]

Вспомним, что wte — это матрица [n_vocab, n_embd]. Она используется в качестве таблицы поиска, где i-тая строка в матрице соответствует обученному вектору для i-того токена в нашем вокабуляре. В wte[inputs] используется целочисленная индексация массива для получения векторов, соответствующих каждому токену во вводе.

Как и любой другой параметр в нашей сети, wte обучается. То есть она случайным образом инициализируется в начале обучения и обновляется при помощи градиентного спуска.

Позиционные эмбеддинги


Особенность архитектуры трансформера заключается в том, что он не учитывает позицию. То есть если мы случайным образом перемешаем наш ввод, а затем соответствующим образом вернём порядок в выводе, то вывод будет таким же, как если бы мы не перемешивали ввод (порядок вводов никак не влияет на вывод).

Разумеется, порядок слов — критически важная часть языка, поэтому нам каким-то образом нужно закодировать во ввод информацию о позиции. Для этого можно использовать ещё одну обученную матрицу эмбеддингов:

wpe[range(len(inputs))] # [n_seq] -> [n_seq, n_embd]

Напомню, что wpe — это матрица [n_ctx, n_embd]. i-тая строка матрицы содержит вектор, кодирующий информацию о i-той позиции ввода. Аналогично wte, эта матрица обучается во время градиентного спуска.

Обратите внимание, что это ограничивает нашу модель максимальной длиной последовательности n_ctx. [В исходной научной статье о трансформере использовался вычисленный позиционный эмбеддинг, показатели качества которого оказались столь же высокими, что и у обученных позиционных эмбеддингов, однако он обладал преимуществом: в качестве ввода можно использовать последовательность любой произвольной длины (максимальная длина последовательности не ограничена). Однако на практике модель будет хороша только при тех длинах последовательностей, на которых она обучалась. Нельзя просто обучить GPT на последовательностях длиной 1024 и ожидать, что она будет хорошо показывать себя на токенах длиной 16 тысяч. Однако в последнее время исследователи добились некоторых успехов с относительными позиционными эмбеддингами, например, Alibi и RoPE] То есть всегда должно быть верно len(inputs) <= n_ctx.

Комбинированный эмбеддинг


Мы можем сложить наш эмбеддинги токенов и позиционные эмбеддинги, чтобы получить комбинированный эмбеддинг, кодирующий информацию и токенов, и позиций.

# эмбеддинги токенов + позиционные эмбеддинги
x = wte[inputs] + wpe[range(len(inputs))]  # [n_seq] -> [n_seq, n_embd]
    
# x[i] обозначает эмбеддинг слова для i-того слова + позиционный
# эмбеддинг для i-той позиции

Стек декодера


Именно здесь происходит вся магия и возникает вся «глубина» глубинного обучения. Мы пропускаем наш эмбеддинг через стек блоков декодера трансформера n_layer.

# прямой проход через блоки трансформера n_layer
for block in blocks:
    x = transformer_block(x, **block, n_head=n_head)  # [n_seq, n_embd] -> [n_seq, n_embd]

Именно составление в стек большего количества слоёв позволяет нам управлять глубиной нашей сети. Например, GPT-3 имеет аж целых 96 слоёв. С другой стороны, выбор большего значения n_embd позволяет нам управлять шириной сети (например, GPT-3 использует размер эмбеддингов 12288).

Проецирование на вокабулярий


На последнем этапе мы проецируем вывод последнего блока трансформера на распределение вероятностей по вокабулярию:

# проецирование на вокабулярий
x = layer_norm(x, **ln_f)  # [n_seq, n_embd] -> [n_seq, n_embd]
return x @ wte.T  # [n_seq, n_embd] -> [n_seq, n_vocab]

Здесь стоит отметить пару моментов:

  1. Сначала мы пропускаем x через слой нормализации последнего слоя, и только после этого выполняем проецирование на вокабулярий. Это особенность архитектуры GPT-2 (она отсутствует в исходных статьях о GPT и трансформере).
  2. Для проецирования мы повторно используем матрицу эмбеддингов wte. В других реализациях GPT для проецирования может использоваться отдельная обученная матрица весов, однако использование той же матрицы имеет пару преимуществ:

    • Мы экономим некоторые параметры (впрочем, при масштабах GPT-3 это несущественно).
    • Так как матрица отвечает и за сопоставление со словами, и из слов, теоретически, она может научиться более богатому описанию, чем при использовании двух отдельных матриц.
  3. Мы не применяем softmax в конце, поэтому выводы будут логитами, а не вероятностями от 0 до 1. Это сделано по множеству причин:
    • softmax — монотонная функция, поэтому для жадного сэмплирования np.argmax(logits) эквивалентна np.argmax(softmax(logits)); следовательно, softmax становится избыточным
    • softmax необратим, то есть мы всегда можем перейти от логитов к вероятностям, применив softmax, но не сможем вернуться к логитам от вероятностей, поэтому для максимальной гибкости мы выводим логиты
    • Численная устойчивость (например, при вычислении потерь перекрёстной энтропии использование log(softmax(logits)) численно неустойчиво по сравнению с log_softmax(logits))

Этап проецирования на вокабулярий иногда также называют головой языкового моделирования. Что означает «голова»? После завершения предварительного обучения GPT можно заменить голову языкового моделирования на другой тип проецирования, например, на голову классификации для подстройки модели под какую-то задачу классификации. То есть модель может иметь несколько голов, напоминая гидру.

Итак, вот как вкратце выглядит архитектура GPT. Давайте немного углубимся в описание того, что делают блоки декодера.

Блок декодера


Блок декодера трансформера состоит из двух подслоёв:

  1. Multi-head causal self attention
  2. Position-wise feed forward neural network


def transformer_block(x, mlp, attn, ln_1, ln_2, n_head):  # [n_seq, n_embd] -> [n_seq, n_embd]
    # multi-head causal self attention
    x = x + mha(layer_norm(x, **ln_1), **attn, n_head=n_head)  # [n_seq, n_embd] -> [n_seq, n_embd]

    # position-wise feed forward network
    x = x + ffn(layer_norm(x, **ln_2), **mlp)  # [n_seq, n_embd] -> [n_seq, n_embd]

    return x

Каждый подслой использует для своих вводов нормализацию слоя, а также остаточную связь (например, добавляет ввод подслоя к выводу подслоя).

Стоит обратить внимание на следующие моменты:

  1. Multi-head causal self attention упрощает коммуникацию между вводами. Больше нигде в сети модель не позволяет вводам «видеть» друг друга. Эмбеддинги, position-wise feed forward network, нормы слоёв и проецирование на вокабулярий обрабатывают вводы с учётом позиции. Задача моделирования связей между вводами полностью отдаётся вниманию.
  2. Position-wise feed forward neural network — это просто двухслойная полностью соединённая нейронная сеть. Она всего лишь добавляет набор изучаемых параметров, с которыми будет работать модель, чтобы упростить обучение.
  3. В исходной научной статье о трансформере норма слоя помещается в вывод layer_norm(x + sublayer(x)), в то время как мы помещаем норму слоя во ввод x + sublayer(layer_norm(x)), чтобы соответствовать GPT-2. Это называется квазинормой; доказано, что она важна для повышения качества работы трансформера.
  4. Остаточные связи (популяризированные ResNet) выполняют несколько задач:

    1. Упрощают оптимизацию глубоких нейронных сетей (то есть сетей, имеющих множество слоёв). Идея заключается в том, что они создают «короткие пути» градиентов для их обратного потока по сети, что упрощает оптимизацию начальных слоёв сети.
    2. В случае отсутствия остаточных связей при добавлении в глубокие модели новых слоёв происходит ухудшение их характеристик (вероятно, потому, что градиентам сложно вернуться назад через всю глубокую сеть без потери информации). Похоже, остаточные связи повышают точность глубоких сетей.
    3. Помогают справиться с проблемой исчезающих/взрывающихся градиентов.

Давайте чуть глубже рассмотрим эти два подслоя.

Position-wise Feed Forward Network


Это всего лишь простой перцептрон с двумя слоями:

def ffn(x, c_fc, c_proj):  # [n_seq, n_embd] -> [n_seq, n_embd]
    # проецируем вверх
    a = gelu(linear(x, **c_fc))  # [n_seq, n_embd] -> [n_seq, 4*n_embd]

    # снова проецируем вниз
    x = linear(a, **c_proj)  # [n_seq, 4*n_embd] -> [n_seq, n_embd]

    return x

Здесь нет ничего особо сложного, мы просто выполняем проецирование n_embd в более высокую размерность 4*n_embd, а затем обратно в n_embd. [В других моделях GPT может использоваться другая скрытая ширина, отличающаяся от 4*n_embd, однако это распространённая практика для моделей GPT. Кроме того, мы уделяем multi-head attention layer много внимания, чтобы он обеспечивал успех трансформера, однако при масштабах GPT-3 80% параметров модели находятся в feed forward layer. Об этом стоит поразмыслить.]

Вспомним, что в словаре params параметры mlp выглядят следующим образом:

"mlp": {
    "c_fc": {"b": [4*n_embd], "w": [n_embd, 4*n_embd]},
    "c_proj": {"b": [n_embd], "w": [4*n_embd, n_embd]},
}

Multi-Head Causal Self Attention


Вероятно, этот слой в трансформере понять сложнее всего. Поэтому давайте начнём разбираться с «Multi-Head Causal Self Attention», разбив его на слова и выделив каждом из них свой раздел:

  1. Attention
  2. Self
  3. Causal
  4. Multi-Head

Attention (внимание)


У меня есть другой пост по этой теме, где мы с нуля выводим уравнение масштабированного скалярного произведения, предложенную в исходной научной статье о трансформере:

$\text{attention}(Q, K, V) = \text{softmax}(\frac{QK^T}{\sqrt{d_k}})V$


Поэтому я не буду приводить в этом посте объяснение того, что такое attention (внимание). Вы также можете изучить Attention? Attention! Лилиан Венг и The Illustrated Transformer Джея Аламмара, где тоже замечательно объясняется, что такое внимание.

Мы просто адаптируем реализацию внимания из моего поста:

def attention(q, k, v):  # [n_q, d_k], [n_k, d_k], [n_k, d_v] -> [n_q, d_v]
    return softmax(q @ k.T / np.sqrt(q.shape[-1])) @ v

Self


Если q, k и v берутся из одного источника, мы выполняем self-attention («внимание к себе») (то есть позволяем последовательности ввода проявить внимание к самой себе):

def self_attention(x): # [n_seq, n_embd] -> [n_seq, n_embd]
    return attention(q=x, k=x, v=x)

Например, если ввод выглядит как "Jay went to the store, he bought 10 apples.", мы можем позволить слову «he» обратить внимание на все остальные слова, включая «Jay», то есть модель сможет научиться определять, что «he» относится к «Jay».

Мы можем усилить внимание к себе, добавив проекции для q, k, v и вывод внимания:

def self_attention(x, w_k, w_q, w_v, w_proj): # [n_seq, n_embd] -> [n_seq, n_embd]
    # проекции qkv
    q = x @ w_k # [n_seq, n_embd] @ [n_embd, n_embd] -> [n_seq, n_embd]
    k = x @ w_q # [n_seq, n_embd] @ [n_embd, n_embd] -> [n_seq, n_embd]
    v = x @ w_v # [n_seq, n_embd] @ [n_embd, n_embd] -> [n_seq, n_embd]

    # выполняем внимание к себе (self attention)
    x = attention(q, k, v) # [n_seq, n_embd] -> [n_seq, n_embd]

    # проекция вывода
    x = x @ w_proj # [n_seq, n_embd] @ [n_embd, n_embd] -> [n_seq, n_embd]

    return x

Это позволяет нашей модели научиться сопоставлению q, k и v, что лучше всего помогает вниманию определять взаимосвязи между вводами.

Мы можем уменьшить количество умножений матриц с четырёх всего до двух, если скомбинируем w_q, w_k и w_v в единую матрицу w_fc, выполним проецирование, а затем разделим результат:

def self_attention(x, w_fc, w_proj): # [n_seq, n_embd] -> [n_seq, n_embd]
    # проекции qkv
    x = x @ w_fc # [n_seq, n_embd] @ [n_embd, 3*n_embd] -> [n_seq, 3*n_embd]

    # разделяем на qkv
    q, k, v = qkv = np.split(x, 3, axis=-1) # [n_seq, 3*n_embd] -> 3 of [n_seq, n_embd]

    # выполняем self attention
    x = attention(q, k, v) # [n_seq, n_embd] -> [n_seq, n_embd]

    # проекция вывода
    x = x @ w_proj # [n_seq, n_embd] @ [n_embd, n_embd] = [n_seq, n_embd]

    return x

Это будет чуть более эффективно, поскольку современные ускорители (GPU) быстрее выполняют умножение одной большой матрицы, чем умножение трёх отдельных маленьких, которое происходит по очереди.

Далее мы добавляем векторы перекоса, чтобы соответствовать реализации GPT-2, используем функцию linear и переименовываем параметры, чтобы они соответствовали словарю params:

def self_attention(x, c_attn, c_proj): # [n_seq, n_embd] -> [n_seq, n_embd]
    # проекции qkv
    x = linear(x, **c_attn) # [n_seq, n_embd] -> [n_seq, 3*n_embd]

    # разделяем на qkv
    q, k, v = qkv = np.split(x, 3, axis=-1) # [n_seq, 3*n_embd] -> 3 of [n_seq, n_embd]

    # выполняем self attention
    x = attention(q, k, v) # [n_seq, n_embd] -> [n_seq, n_embd]

    # проекция вывода
    x = linear(x, **c_proj) # [n_seq, n_embd] @ [n_embd, n_embd] = [n_seq, n_embd]

    return x

Вспомним из словаря params, что параметры attn выглядят так:

"attn": {
    "c_attn": {"b": [3*n_embd], "w": [n_embd, 3*n_embd]},
    "c_proj": {"b": [n_embd], "w": [n_embd, n_embd]},
},

Causal


У нашей текущей схемы с self-attention есть небольшая проблема: наши вводы могут видеть будущее! Например, если ввод имеет вид ["not", "all", "heroes", "wear", "capes"], то во время этапа self attention мы позволяем «wear» увидеть «capes». Это означает, что выходные вероятности для «wear» будут перекошены, поскольку модель уже знает, что правильный ответ — это «capes». И это плохо, ведь наша модель просто узнает, что правильный ответ для ввода $i$ можно взять из ввода $i+1$.

Чтобы предотвратить это, нам нужно каким-то образом преобразовать матрицу внимания, чтобы скрыть или маскировать вводы, не позволив им смотреть в будущее. Например, пусть наша матрица внимания выглядит так:

       not    all    heroes wear   capes
   not 0.116  0.159  0.055  0.226  0.443
   all 0.180  0.397  0.142  0.106  0.175
heroes 0.156  0.453  0.028  0.129  0.234
  wear 0.499  0.055  0.133  0.017  0.295
 capes 0.089  0.290  0.240  0.228  0.153

Каждая строка соответствует запросу, а столбец — ключу. В этом случае, взглянув на строку «wear», можно увидеть, что он обращает внимание на «capes» в последнем столбце с весом 0.295. Чтобы избежать этого, нужно присвоить этому элементу значение 0.0:

      not    all    heroes wear   capes
   not 0.116  0.159  0.055  0.226  0.443
   all 0.180  0.397  0.142  0.106  0.175
heroes 0.156  0.453  0.028  0.129  0.234
  wear 0.499  0.055  0.133  0.017  0.
 capes 0.089  0.290  0.240  0.228  0.153

В общем случае, чтобы предотвратить заглядывание всех запросов во вводе в будущее, мы присваиваем всем позициям $i, j$ (где $j > i$) значение 0:

       not    all    heroes wear   capes
   not 0.116  0.     0.     0.     0.
   all 0.180  0.397  0.     0.     0.
heroes 0.156  0.453  0.028  0.     0.
  wear 0.499  0.055  0.133  0.017  0.
 capes 0.089  0.290  0.240  0.228  0.153

Это называется маскированием. Проблема такого решения заключается в том, что сумма строк больше не равна 1 (так как мы обнуляем их после применения softmax). Чтобы строки снова в сумме давали 1, нужно изменять матрицу внимания до применения softmax.

Этого можно достичь, присваивая элементам, которые будут маскированы, значение $-\infty$ перед выполнением softmax. [Если вы в этом не уверены, то внимательно присмотритесь к уравнению softmax, и убедитесь, что это так (возможно, вам понадобятся ручка с бумагой):

$\text{softmax}(\vec{x})_i=\frac{e^{x_i}}{\sum_je^{x_j}}$

]

def attention(q, k, v, mask):  # [n_q, d_k], [n_k, d_k], [n_k, d_v], [n_q, n_k] -> [n_q, d_v]
    return softmax(q @ k.T / np.sqrt(q.shape[-1]) + mask) @ v

где mask — это матрица (для n_seq=5):

0 -1e10 -1e10 -1e10 -1e10
0   0   -1e10 -1e10 -1e10
0   0     0   -1e10 -1e10
0   0     0     0   -1e10
0   0     0     0     0

Мы используем -1e10 вместо -np.inf поскольку -np.inf может вызывать nan.

Сложение mask с матрицей внимания вместо присваивания значений -1e10 срабатывает, потому что на практике любое число плюс -inf тоже равно -inf.

Мы можем вычислить матрицу mask в NumPy при помощи (1 - np.tri(n_seq)) * -1e10.

Соединив всё вместе, получим:

def attention(q, k, v, mask):  # [n_q, d_k], [n_k, d_k], [n_k, d_v], [n_q, n_k] -> [n_q, d_v]
    return softmax(q @ k.T / np.sqrt(q.shape[-1]) + mask) @ v

def causal_self_attention(x, c_attn, c_proj): # [n_seq, n_embd] -> [n_seq, n_embd]
    # проекции qkv
    x = linear(x, **c_attn) # [n_seq, n_embd] -> [n_seq, 3*n_embd]

    # разделяем на qkv
    q, k, v = qkv = np.split(x, 3, axis=-1) # [n_seq, 3*n_embd] -> 3 of [n_seq, n_embd]

    # маска каузальности для сокрытия будущих вводов от внимания
    causal_mask = (1 - np.tri(x.shape[0])) * -1e10  # [n_seq, n_seq]

    # выполняем causal self attention
    x = attention(q, k, v, causal_mask) # [n_seq, n_embd] -> [n_seq, n_embd]

    # проекция вывода
    x = linear(x, **c_proj) # [n_seq, n_embd] @ [n_embd, n_embd] = [n_seq, n_embd]

    return x

Multi-Head


Мы можем усовершенствовать нашу реализацию, выполнив отдельные вычисления внимания n_head, разделив запросы, ключи и значения в головы:

def mha(x, c_attn, c_proj, n_head):  # [n_seq, n_embd] -> [n_seq, n_embd]
    # проекция qkv
    x = linear(x, **c_attn)  # [n_seq, n_embd] -> [n_seq, 3*n_embd]

    # разделяем на qkv
    qkv = np.split(x, 3, axis=-1)  # [n_seq, 3*n_embd] -> [3, n_seq, n_embd]

    # разделяем на головы
    qkv_heads = list(map(lambda x: np.split(x, n_head, axis=-1), qkv))  # [3, n_seq, n_embd] -> [3, n_head, n_seq, n_embd/n_head]

    # маска каузальности для сокрытия будущих вводов от внимания
    causal_mask = (1 - np.tri(x.shape[0])) * -1e10  # [n_seq, n_seq]

    # выполняем внимание для каждой головы
    out_heads = [attention(q, k, v, causal_mask) for q, k, v in zip(*qkv_heads)]  # [3, n_head, n_seq, n_embd/n_head] -> [n_head, n_seq, n_embd/n_head]

    # объединяем головы
    x = np.hstack(out_heads)  # [n_head, n_seq, n_embd/n_head] -> [n_seq, n_embd]

    # проекция вывода
    x = linear(x, **c_proj)  # [n_seq, n_embd] -> [n_seq, n_embd]

    return x

Здесь мы добавили три этапа:

  1. Разделение q, k, v на головы n_head:
    # разделяем на головы
qkv_heads = list(map(lambda x: np.split(x, n_head, axis=-1), qkv))  # [3, n_seq, n_embd] -> [n_head, 3, n_seq, n_embd/n_head]
  2. Вычисляем внимание для каждой головы:

    # выполняем внимание для каждой головы
out_heads = [attention(q, k, v) for q, k, v in zip(*qkv_heads)]  # [n_head, 3, n_seq, n_embd/n_head] -> [n_head, n_seq, n_embd/n_head]
  3. Объединяем выводы каждой головы:

    # объединяем головы
x = np.hstack(out_heads)  # [n_head, n_seq, n_embd/n_head] -> [n_seq, n_embd]

Обратите внимание, что это снижает размерность с n_embd до n_embd/n_head для каждого вычисления внимания. Это компромисс. В обмен на снижение размерности наша модель получает дополнительные подпространства для работы при моделировании отношений при помощи внимания. Например, одна голова внимания может отвечать за сопоставление местоимений с человеком, к которому относятся местоимения. Другая может отвечать за группировку предложений по периодам. Третья может просто определять, какие из слов являются сущностями, а какие нет. Однако, вероятнее будет, что это просто ещё один «чёрный ящик» нейронной сети.

Написанный нами код последовательно в цикле (по одному за раз) выполняет вычисления внимания для каждой из голов, что не особо эффективно. На практике это хотелось бы делать параллельно. Для простоты мы оставим последовательную обработку.

И на этом мы завершили свою реализацию GPT! Осталось соединить всё вместе и выполнить код.

Соединяем всё вместе


Соединив всё вместе, мы получили gpt2.py, состоящий всего лишь из 120 строк кода (60 строк, если убрать комментарии и пробелы).

Мы можем протестировать свою реализацию так:

python gpt2.py \
    "Alan Turing theorized that computers would one day become" \
    --n_tokens_to_generate 8

И получим следующий вывод:

the most powerful machines on the planet.

Работает!

Мы можем убедиться, что наша реализация даёт идентичные с официальным репозиторием GPT-2 компании OpenAI результаты, воспользовавшись следующим Dockerfile. (Предупреждение: из-за особенностей tensorflow это не сработает на Macbook с M1; кроме того, при этом скачаются все четыре размера GPT-2, то есть объём скачиваемого в гигабайтах будет приличным):

docker build -t "openai-gpt-2" "https://gist.githubusercontent.com/jaymody/9054ca64eeea7fad1b58a185696bb518/raw/Dockerfile"
docker run -dt "openai-gpt-2" --name "openai-gpt-2-app"
docker exec -it "openai-gpt-2-app" /bin/bash -c 'python3 src/interactive_conditional_samples.py --length 8 --model_type 124M --top_k 1'
# paste "Alan Turing theorized that computers would one day become" when prompted

Это должно дать идентичный результат:

the most powerful machines on the planet.

Что дальше?


Конечно, это прекрасная реализация, но в ней отсутствует куча возможностей:

Поддержка GPU/TPU


Заменим NumPy на JAX:

import jax.numpy as np

Вот и всё. Теперь можно использовать код с GPU и даже с TPU!

Обратное распространение (Backpropagation)


Снова заменим NumPy на JAX:

import jax.numpy as np

Тогда для вычисления градиентов достаточно будет следующего:

def lm_loss(params, inputs, n_head) -> float:
    x, y = inputs[:-1], inputs[1:]
    output = gpt2(x, **params, n_head=n_head)
    loss = np.mean(-np.log(output[y]))
    return loss

grads = jax.grad(lm_loss)(params, inputs, n_head)

Батчинг


Мы снова заменяем NumPy на JAX:

import jax.numpy as np

Теперь чтобы добавить в функцию gpt2 батчинг, достаточно следующего:

gpt2_batched = jax.vmap(gpt2, in_axes=[0, None, None, None, None, None])
gpt2_batched(batched_inputs) # [batch, seq_len] -> [batch, seq_len, vocab]

Оптимизация Inference


Наша реализация довольно неэффективная. Самое быстрая и важная оптимизация, которую можно добавить (если не считать GPU + батчинг) — это реализация кэша kv, чего можно добиться, изменив несколько строк кода. Кроме того, мы реализовали вычисления голов внимания последовательно, а на самом деле они должны выполняться параллельно. [При использовании JAX для этого достаточно написать heads = jax.vmap(attention, in_axes=(0, 0, 0, None))(q, k, v, causal_mask).]

Существует ещё множество других оптимизаций inference. В качестве начальной точки рекомендую Large Transformer Model Inference Optimization Лилиан Венг и Transformer Inference Arithmetic Kipply.

Обучение


Если не считать объёмов, обучение GPT — это довольно стандартный процесс, градиентный спуск относительно потерь языковой модели. Разумеется, существует ещё множество хитростей (использование оптимизации Adam, нахождение оптимальной скорости обучения, регуляризация при помощи выключения и/или уменьшения весов, планировщики скорости обучения, логика заполнения последовательностей, инициализация весов, батчинг и так далее...), но всё это довольно стандартные вещи.

Настоящий секретный ингредиент обучения хорошей модели GPT — возможность масштабирования данных и модели.

Для масштабирования данных нужен большой, качественный и разнообразный корпус текстов.

  • Большой — это миллиарды токенов (терабайтов данных). Например, оцените The Pile — опенсорсный датасет предварительного обучения для больших языковых моделей.
  • Под высоким качеством подразумевается, что необходимо отфильтровывать дублирующиеся примеры, неотформатированный текст, бессвязный текст, мусорный текст и так далее
  • Под разнообразием подразумеваются различные длины последовательностей, множество различных тем, тексты из разнообразных источников с разными точками зрения и так далее. Разумеется, если в данных есть какие-то перекосы, то это отразится на модели, поэтому с этим тоже нужно быть аккуратными.

Для масштабирования модели до миллиардов параметров требуется куча труда разработчиков (и денег). Фреймворки обучения могут становиться абсурдно долгими и сложными. Начать изучение можно с How to Train Really Large Models on Many GPUs Лилиан Венг. По этой теме также есть Megatron Framework компании NVIDIA, Training Framework компании Cohere, PALM компании Google, опенсорсный mesh-transformer-jax (использованный для обучения опенсорсных моделей EleutherAI) и множество других источников.

Оценка


Как же можно оценивать LLM? Честно говоря, это очень сложно. Неплохо начать с HELM, но к бенчмаркам и метрикам оценок всегда стоит относиться скептически.

Улучшения архитектуры


Рекомендую изучить X-Transformers Фила Вана. Это самое новое и качественное исследование архитектуры трансформеров. Также вполне качественное резюме есть в этой статье.

Комментарии (5)


  1. MAXH0
    00.00.0000 00:00
    #25252640
    +2

    Большое спасибо! GPT сейчас рассматривают, чаще, со стороны пользователей. НО программная реализация тоже интересна. Надеюсь, что мы рано или поздно получим не просто ботов обученных корпорациями, а AI действительно свободный и который можно подстроить под себя (например, приобретая предобученные нейросети)...

    По поводу ботов есть история почти офтоп, но которая показывает ход моих мыслей. Знакомая разочаровалась в умной колонке. Умная колонка стала учить её пятилетнею дочь требовать купить смартфон. И это интеллект именно простого бота. А когда корпорации получат более интеллектуальные механизмы мы, со своей потребностью в антропоморфизме всего и вся, легко подсядем на мнения "из машины".


    1. artemev
      00.00.0000 00:00
      #25253056
      +1

      Умная колонка стала учить её пятилетнею дочь требовать купить смартфон.

      С удовольствием почитал бы статью об этом. Очень интересно!


    1. jasiejames
      00.00.0000 00:00
      #25255930

      По поводу ботов есть история почти офтоп))))

      Такая была же у Кэмерона и Вачовски, мы вроде же это тыщу раз обсудили???


  1. jasiejames
    00.00.0000 00:00
    #25255926
    -1

    Чувачок, статья неплохая, убирай картинки под "кат", сейчас заклюют тебя)))


  1. Tzimie
    00.00.0000 00:00
    #25256082

    А есть такие же классификаторы изображений, которые можно натренировать самому?