В 1655 году английский математик Джон Валлис опубликовал трактат «Арифметика бесконечного», где вывел формулу числа ? из произведения бесконечного ряда дробей, которые постепенно сходятся.
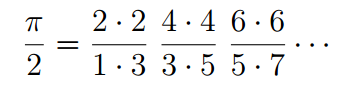
Формула Валлиса мало пригодна для практических вычислений, но была полезна во многих теоретических исследованиях. Теперь математики из университета Рочестера (США) внезапно обнаружили, что та же самая формула подходит для описания квантово-механических энергетических уровней атома водорода. Это означает наличие прямой связи реального мира физики и абстрактного мира чистой математики.
«Мы не искали специально формулу Валлиса для ?. Она сама попала к нам в руки, — говорит Карл Хаген (Carl Hagen), соавтор научной статьи "Quantum mechanical derivation of the Wallis formula for ?", опубликованной в «Журнале математической физики».
«Для нас это стало полной неожиданностью — я буквально запрыгал в тот момент, когда мы вывели формулу Валлиса из уравнений для атомов водорода, — признался его коллега Тамар Фридманн (Tamar Friedmann) из университета Рочестера. Что главное в этом – наше открытие красивым образом соединяет физику и математику. Меня поражает то, как чисто математическая формула из 17 века характеризует физическую систему, которая была открыта только через 300 лет после её выведения».
Странную закономерность первым заметил Карл Хаген совершенно случайно. Он решал со студентами задачку по расчёту положений энергоуровней атома водорода. Для этого используются особые версии уравнения Шрёдингера. В то же время значения энергоуровней хорошо известны из реальных экспериментов.
Вместе со студентами преподаватель обратил внимание, что разброс в предсказанных и реальных положениях энергоуровней следовал некой математической закономерности, двигаясь от нижних к верхним уровням. К примеру, уровень ошибки для первого уровня, где находится единственный электрон водорода, составлял 15%, для второго — 10% и так далее.
Хакен обратился за помощью к Фридманну, математику по образованию. Тот и вспомнил о старой формуле Валлиса. Оказалось, что соотношение дробей в формуле в точности соответствует разбросу между реальными и вычисленными значениями энергетических уровней.

На низкоэнергетической орбите положение электрона нечёткое и размытое, а в более возбуждённом состоянии орбиты становятся более чётко определёнными и ошибка в предсказании положения электрона и радиуса орбиты уменьшается.
Теория квантовой механики была сформулирована в начале 20 века, а формула Валлиса известна веками, но связи между ними прежде никто не видел: «Природа хранила этот секрет последние 80 лет, — говорит Фридманн. — Я рад, что нам удалось его раскрыть».
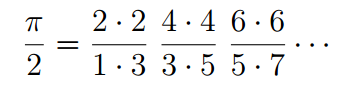
Формула Валлиса мало пригодна для практических вычислений, но была полезна во многих теоретических исследованиях. Теперь математики из университета Рочестера (США) внезапно обнаружили, что та же самая формула подходит для описания квантово-механических энергетических уровней атома водорода. Это означает наличие прямой связи реального мира физики и абстрактного мира чистой математики.
«Мы не искали специально формулу Валлиса для ?. Она сама попала к нам в руки, — говорит Карл Хаген (Carl Hagen), соавтор научной статьи "Quantum mechanical derivation of the Wallis formula for ?", опубликованной в «Журнале математической физики».
«Для нас это стало полной неожиданностью — я буквально запрыгал в тот момент, когда мы вывели формулу Валлиса из уравнений для атомов водорода, — признался его коллега Тамар Фридманн (Tamar Friedmann) из университета Рочестера. Что главное в этом – наше открытие красивым образом соединяет физику и математику. Меня поражает то, как чисто математическая формула из 17 века характеризует физическую систему, которая была открыта только через 300 лет после её выведения».
Странную закономерность первым заметил Карл Хаген совершенно случайно. Он решал со студентами задачку по расчёту положений энергоуровней атома водорода. Для этого используются особые версии уравнения Шрёдингера. В то же время значения энергоуровней хорошо известны из реальных экспериментов.
Вместе со студентами преподаватель обратил внимание, что разброс в предсказанных и реальных положениях энергоуровней следовал некой математической закономерности, двигаясь от нижних к верхним уровням. К примеру, уровень ошибки для первого уровня, где находится единственный электрон водорода, составлял 15%, для второго — 10% и так далее.
Хакен обратился за помощью к Фридманну, математику по образованию. Тот и вспомнил о старой формуле Валлиса. Оказалось, что соотношение дробей в формуле в точности соответствует разбросу между реальными и вычисленными значениями энергетических уровней.
На низкоэнергетической орбите положение электрона нечёткое и размытое, а в более возбуждённом состоянии орбиты становятся более чётко определёнными и ошибка в предсказании положения электрона и радиуса орбиты уменьшается.
Теория квантовой механики была сформулирована в начале 20 века, а формула Валлиса известна веками, но связи между ними прежде никто не видел: «Природа хранила этот секрет последние 80 лет, — говорит Фридманн. — Я рад, что нам удалось его раскрыть».


ankh1989
Говорит ли это в пользу того, что мир — симуляция? :)
zuborg
Скорее это говорит, что в стоении атома водорода где-то участвует круг.
mphys
Там во многих уравнениях есть pi, на самом деле, даже там где о кругах речи нет :)
Halt
На Арбузе есть отличная статья на эту тему: «Мировые константы пи и е в основных законах физики и физиологии»
qbertych
Есть чудесный результат Гейма и Новоселова про поглощение света в графене. Оказывается он поглощает 2,3%, что в точности равняется числу пи, умноженному на постоянную тонкой структуры =).

Halt
Ну в связи константы ? с изотропностью пространства все логично, ибо поглощение происходит в сферически однородном пространстве. В описании временны?х характеристик процесса должно и число е присутствовать, вследствие изотропности времени.
Eol
Тут то совершенно никакой изотропности пространства нет. Лист графена двумерный, на него перпендикулярно падает свет. У системы есть выделенное направление. И буква e тут — заряд электрона, если что. Как оно связано с изотропностью по времени?
Halt
По вашему при стрельбе из ружья перпендикулярно по мишени тоже изотропности пространства нет?
Про то что заряд электрона и число Эйлера — разные сущности я и сам понимаю и говорил именно про второе.
qbertych
— Снаряд из пушки летит по параболе.
— Товарищ майор, а если пушку на бок положить, то и за угол стрелять можно будет?
— Можно. Но по уставу не положено!
Eol
Развивая аналогию. По-моему при стрельбе ружья и при исследовании того, как пуля будет пробивать стену, изотропности не будет. Результат явно будет зависеть от того, перпендикулярно ли мы стреляем или по касаетельной.
Прошу прощения. Но как тогда число Эйлера связано с однородностью времени?
qbertych
А вы почитайте. Постоянная тонкой структуры появляется из проводимости графена. Это чисто двумерная задача, изотропности ни при чем.
Halt
Так причем тут постоянная тонкой структуры? Я про пи говорю. Во-вторых, и у двумерного пространства может быть [не]однородность.
Eol
Задачка эта примечательная. Но в каком-то смысле обидно то, что ответ \pi\ alpha — не строго точный с точки зрения теории — к нему есть малые поправки порядка \alpha^2,3,… Поэтому измерить \alpha таким способом с точностью лучше 1% не получится.
В отличии от, например, другого замечательного явления — квантового эффекта Холла, где квантование поперечной проводимости точное. С его помощью ту же постоянную тонкой структуры измеряют с точностями 10^-7.
Hedgehogues
Это говорит лишь о том, что пока что мы идёт в более менее разумном направлении
ankh1989
Хм… интересная гипотеза про круг.
kbtsiberkin
Берём постоянную Планка, делим на две постоянных Планка с чёрточкой, получаем в точности число пи.
Eugney
Какое поразительное совпадение! Шах и мат, атеисты!
JIghtuse
В треде снай
Valistar
Карлу Сагану бы понравилось. Его роман «Контакт» (в частности) как раз про число ?.
pehat
Почему в «Что? Где? Когда?» за столом 6 человек? Потому что оптимальное количество игроков равно 2?.
Почему оно равно 2?? Потому что стол круглый.
pcholberg
А в Поле чудес 3 игрока, потому что они занимают только половину.
Zenitchik
Вообще-то всё правильно. Почему артиллерийский угломер делит круг на 6000 делений? А всё потому же, чтобы тангенс одного деления был примерно равен 1/1000, но не возникало дробных коэффициентов — и то и другое важно для приблизительных вычислений в уме.
Eol
Ерунда какая-то.
Вообще говоря, при решении студенческих задач по квантовой механике очень часто приходится пользоваться всякими соотношениями из матфизики, выражениями для спецфункций и констант, и т.п.
Значит ли это, что студенты-физики эти соотношения доказывают из физических задач? Конечно, нет. Они пользуются этим в другую сторону.
И задачек таких известно огромное количество, просто буквально из учебников. Удивительно, что профессура это обнаружила с таким удивлением, что аж статью опубликовали.
Конкретно в этом случае автор на самом деле показал, используя формулу Валлиса, что отличие истинных уровней энергии атома водорода и уровней, полученных из приближенной формулы, почти совпадают в пределе больших орбитальных квантовых чисел. Не больше и не меньше.
Если бы он знал это заранее из других соображений — то пожалуйста.
Он, конечно, приводит «правдоподобное рассуждение», почему это похоже на правду, но на доказательство оно не похоже. А вот формула Валлиса вполне себе это доказывает.
Eol
А, на автора посмотрел. Боже, где вы только такое находите?
galaxy
Сама статья — коротенькая, но интересная.

Насчет удивительности: авторам, наверное, кажутся тривиальными и скучными все эти сферические функции и собственные функции гамильтониана атома водорода. Странно, что никаких эмоций у них не вызвал походя ими использованный факт, что
chabapok
А что означает L+1 в верхнем пределе? Конкретно — смущает эта единица. Там же L стремится к бесконечности, так какой математический смысл вкладывается, когда пишут L+1?
Eol
Никакого. Можно писать L, результат, как вы правильно заметили, будет такой же.
В большинстве мест вообще не заморачиваются с написанием \lim и просто пишут произведения от 1 до \infty.
kaichou
Примерно в 250 году до н.э. Архимед дал приближение числа пи как 3 1/7. Он знал?