Начинаем создавать "управляющую" нейронную сеть, автоматически подбирающую гиперпараметры и архитектуры "контролируемых" нейронных сетей.

Постановка задачи

При обучении нейронных сетей часто приходится подбирать гиперпараметры и архитектуры "вручную", "интуитивно", "по ощущениям". Задача - создать алгоритм и программу, подбирающую гиперпараметры и архитектуры для обучения нейронных сетей автоматически.

Начало

Начнем с однослойной сети прямого распространения (FNN), потом будем расширяться, переходя на многослойные сети прямого распространения, на многослойные сверточные сети (CNN) и на "тюнинг" предобученных сетей.

Некоторые исследования уже были проведены, представлены в предыдущей статье "Анализ подбора гиперпараметров при обучении нейронной сети прямого распространения — FNN (на примере MNIST)", и в ряде случаев будем к ним обращаться.

Что уже знаем и умеем:

1. увеличение количества признаков приводит к увеличение точности, но нужно следить за переобучением.

2. переобучение возможно регулировать подбором размера батча и dropout.

3. с определенного момента целесообразно добавлять уменьшение шага обучения и "шлифовать" точность.

Изначально сразу сталкиваемся со следующими неопределенностями:

1. Конечная функция не то чтобы дифференцируема, а пока вообще не известна, то есть не сможем применять в лоб "производные" и соответствующие алгоритмы.

2. Не известна форма поверхности, с которой предстоит работать. Например, в гиперболе один оптимум, в синусоиде - повторяющиеся оптимумы. Если линия под углом, или даже сигмоида, то забираемся как можно дальше, насколько хватит времени и мощности. Если гипербола плюс синусоида, то постоянно попадаем в локальные экстремумы, из которых нужно выбираться, а "импульсы" и "моменты" здесь сразу не применить. То есть представление о форме поверхности может сильно упростить разработку алгоритма, но мы пока о ней ничего не знаем.

Начинаем хоть с чего-то

Посмотрим, с какими поверхностями имеем дело.

Конечно, идеальный случай - сделать полный перебор по количествам признаков и размерам батчей. Однако понимаем, что каждая такая итерация - это полное обучение сети, то есть такой подход слишком затратный. Более того, изменение, например, количества признаков на 1 не дает явного изменения, поэтому лучше перемещаться какими-либо шагами.

Примечания:

1. Альтернатива №1. Аппроксимация.
Теоретически, можно выбрать последовательность количеств признаков, выбрать последовательность размеров батчей, сделать замеры точности и аппроксимировать многомерную функцию. Однако, если замеров делать "мало", то качество аппроксимации представляется сомнительным, а если для допустимого качества аппроксимации делать замеров "много", то это опять же слишком затратно, да и можно сделать так много замеров, что задача поиска оптимума отпадет сама собой, так как замерами составится вполне приличная карта. Если же делать "среднее" количество замеров, то есть определить некоторый ряд количеств признаков и некоторый ряд размеров батчей, то представляется, что предложенный в данной статье алгоритм будет более эффективнее, чем аппроксимация на схожем количестве замеров.

2. Альтернатива №2. Как-бы градиентный спуск.
При обучении нейронных сетей мы часто применяемый градиентный спуск. С некоторыми допущениями и ограничениями возможно применить градиентный спуск и в данном случае. Основное отличие лишь в том, что мы не знаем функцию, поэтому будем просто замерять точность до итерации и точность после итерации. При этом на каждой итерации, кроме первой, точность до итерации будет уже измерена, так как это будет точностью после предыдущей итерации. Также если мы будем учитывать, что обычно направление движения сохраняется с гораздо большей вероятностью, чем изменение на обратное, то на каждой итерации будем сначала делать измерение в том же направлении, и только если показатели ухудшились, то будем измерять показатели движения в обратном направлении. Так, поочередно меняя количество признаков и размер батча, будем продвигаться в сторону экстремума. При этом понимаем, что если начали колебаться "вперед-назад", то подозреваем локальный экстремум. В данном случае шаг не уменьшаем, запоминаем соотношение, выходим из локального экстремума и идем дальше. Когда пройдем заданный интервал или до некоторого заданного ограничения, то возьмем каждый сохраненный локальный экстремум и проработаем со схемами уменьшения шага. Хотя этот алгоритм также представляется "затратным", так как на каждой итерации сеть обучается заново.

Необходимо отметить, что мы ничего не утверждаем и ничего не опровергаем - все подлежит тестированию. Поэтому все альтернативные решения имеют право быть, и даже интересно довести их до реализации и сравнить получившиеся алгоритмы, но это тема уже отдельной статьи.

Возвращаемся к рассматриваемому алгоритму.

В IT любят умножить на 2, поэтому возьмем увеличивающийся в 2 раза ряд количества признаков [ 128, 256, 512, 1024, 4056, 8192 ]. Больше 8192 уже как-то "затратно", хотя возможная целесообразность захождения правее будет быстро понятна в ходе исследования. Меньше 128 тоже вроде бы не имеет смысла, хотя также будет быстро понятно в ходе исследования. И чтобы скачки не были таким уж резкими, вставим дополнительные значения посередине между имеющимися значениями.

Размер батча 64, размер валидационной выборки 20%, оптимизатор 'adam'.
Dropout пока не трогаем, так как при однослойной сети он как-то не очень влияет на экстремум, а шаги обучения будем уменьшать уже непосредственно в зонах экстремума, окончательно шлифуя точность.

Запускаем на 20 эпох, чтобы присмотреться.

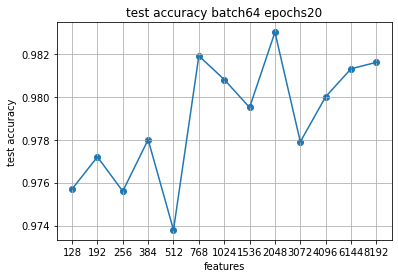
20 эпох - это, конечно, ну очень примерно, хотя мы специально и взяли "очень мало", ни в одном из случаев точность обучающей выборки не доходит до 1.0. Но уже можно сделать вывод, что на одном и том же размере батча точность не растет в ту или иную сторону постоянно и не имеет одного явно выраженного экстремума, а скачет пока неочевидным образом.

На 40 эпохах до 2048 стали уже доходить до 1.0, но ясности это не добавило, а наоборот - картину видим совершенно иную, чем на 20 эпохах.
Хотя уже некоторая зона экстремума прослеживается.

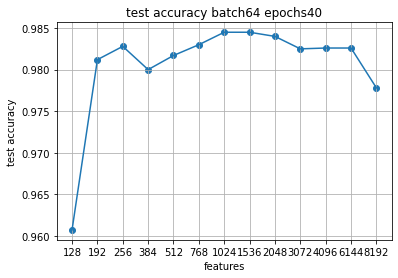
Добавив графики на 60 эпох снова видим примерную зону экстремума.

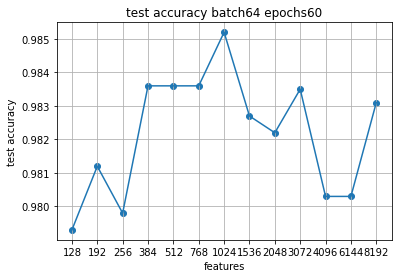
Продолжим на 80 эпох, чтобы дообучились модели с большим количеством признаков.
Скачки немного другие, но зона экстремума примерно там же, где и на 60.

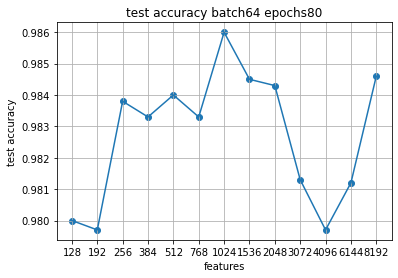
Таким образом видно, что единый экстремум даже по одному размеру батча может и отсутствовать, поэтому следует выделять возможные "зоны экстремума".

Определяем алгоритм в общем виде

Прослеживается деление алгоритма на 3 этапа:

1. определить примерные зоны экстремума (их может быть несколько);

2. в зонах экстремума поработать более пристально и определить "потенциально оптимальные" соотношения количества признаков и размеров батча (их также может быть несколько);

3. передать "потенциально оптимальные" соотношения в "контролируемые" нейронные сети и по каждому соотношению осуществить обучение с несколькими заранее выбранными схемами уменьшения шага обучения.

Важно, что каждый этап представляется "независимым", то есть на входе набор данных и на выходе набор данных, а технологии внутри этапа могут меняться и совершенствоваться независимо от изменений и усовершенствований других этапов.

Также важно, что все последующие вычисления также "независимы" , то есть возможно брать любые части выбранных последовательностей, отправлять их на разные машины, обрабатывать параллельно, а потом объединять результаты. По сути, в итоге получится набор [(параметр 1, параметр 2, ... , точность)]. Это легко объединяется и сравнивается.

Необходимо отметить, что так как обычно обучение начинается со случайно инициированных наборов весов, то никакое соотношение полученных гиперпараметров не гарантирует, что повторные обучения дадут точно эту же точность. То есть если выбранное соотношение дает лучшую точность, а второе соотношение дает точность чуть меньше, то это не означает, что при повторных запусках первое соотношение опять даст лучший результат. Поэтому нужно выбрать не одно "лучшее" соотношение, а несколько, дающих близкие "лучшие" результаты, и потом по несколько раз осуществить повторные запуски. В общем случае, данный процесс возможно считать очередным этапом алгоритма.

1 этап. Определяем зоны экстремума

Идем от простого к сложному. Берем ряд количеств признаков и ряд размеров батчей и делаем полный перебор комбинаций.

Для экономии времени и упрощения визуализации на этапе формирования алгоритма разделяем количества признаков на "малые" (до 1024) и "большие" (более 1024) и запускаем "малые" на 40 эпох.

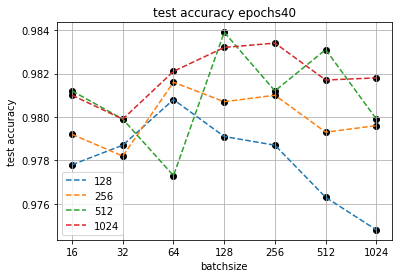
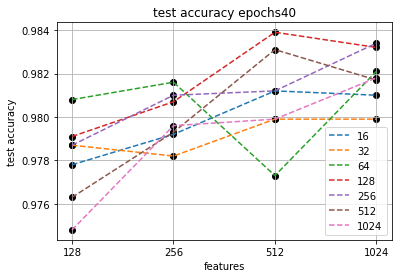
В 3-мерном виде поверхность выглядит так:

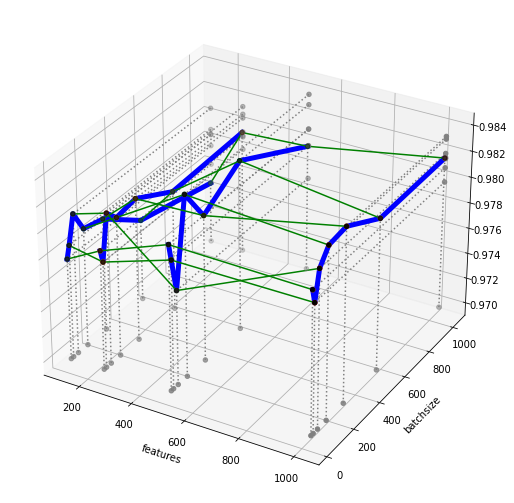
Понимаем, что с "большими" все будет аналогично.

2 этап. Определяем "потенциально оптимальные" соотношения

Видим, что близкие значения точности могут достигаться при разных соотношениях количества признаков и размеров батча. Например показатели точности четырех точек (при количестве признаков 1024 с батчем 512 и 256 и при количестве признаков 512 с батчем 128 и 512) достаточно достаточно близки, предположительно на уровне случайности инициации исходных весов. Это усиливает тезис о необходимости выделения несколько "зон экстремума".

Примечание:
Данная ситуация косвенно говорит еще и о том, что перемещаться градиентным спуском, перемещаясь итерационно поочередно по каждому пространству, в данном случае не целесообразно, так как потенциально "оптимальных" зон несколько, и до каких именно значений можно дойти в каждой зоне - неизвестно до тех пор, пока зона не будет полностью проработана. Вероятность того, что градиентный спуск приведет именно в нужную зону из нескольких крайне мала, на уровне пропорции с учетом количества зон. То есть каждую зону следует прорабатывать отдельно и "параллельно", а потом объединять и сравнивать полученные результаты.

Берем любую зона экстремума и попытаемся разобраться, как работать с этой информацией.

Точка: количество признаков 512, размер батча 128.

Рассмотрим "точку" (512, 128).
Более корректно будет рассматривать не точку, а интервалы (512, [64-256]) и ([256-1024], 128). При фиксации количества признаков или размера батча мы получаем стандартную задачу определения оптимума неизвестной функции на заданном интервале в двухмерном пространстве. Для такой задачи есть уже стандартные известные способы, даже не связанные с нейронными сетями. Понимаем, что мы можем взять "какой-то" способ, и потом его менять, корректировать и прочее, и это будет отдельным фрагментом. На выход будет подаваться только координата оптимума - число признаков и размер батча.

Итак, начнем с самого простого способа - разделим интервал на 8 частей и посчитаем значение в соответствующих точках. Где значение больше - там и оптимум.

Таким образом рассмотрим все выявленные зоны экстремума и получим набор "потенциально оптимальных" соотношений количеств признаков и размеров батчей.
Важно отметить, что на данном этапе не так важно, как именно находить экстремум на заданном интервале. На данном этапе достаточно того, что способы существуют, их несколько, их можно перебрать и выбрать один или несколько.

3 этап. Шлифуем точность

К этому моменту определен набор "потенциально оптимальных" соотношений количеств признаков и размеров батчей. Осталось только по очереди отправить данные соотношения в "контролируемую" сеть и с каждым соотношением применить несколько заранее выбранных схем уменьшения шага обучения.

Некоторые из распространенных схем уменьшения шага обучения:

1. Не уменьшать шаг обучения.

2. Уменьшать шаг обучение в 2 раза через заданное количество эпох (часто 7).

3. Уменьшать шаг обучения в 2 раза, если через заданное количество эпох точность не увеличивается (часто 3).

4. Уменьшать шаг обучения в 2 раза, если через "сильно большее" количество эпох точность не увеличивается (например, 10).

Теперь запускается цикл перебора по набору "потенциально оптимальных" соотношений, и по каждому соотношению из набора запускается вложенный цикл перебора по выбранным схемам уменьшения шага обучения. В итоге выбирается несколько лучших значений (3,5,7), запоминаются, и запускаются несколько раз для усреднения случайностей.

Предварительные результаты

На данном этапе получили теоретический алгоритм, дающий на выходе оптимальное соотношение количества признаков, размера батча и схемы уменьшения шага обучения для однослойной сети прямого распространения. В случае если алгоритм работоспособен, то в него возможно добавлять новые параметры и расширять до многослойных сетей прямого распространения, многослойных сверточных сетей и "тюнинга" предобученных сетей, получив таким образом "управляющую" нейронную сеть для автоматического подбора гиперпараметров и архитектур "контролируемых" нейронных сетей.

Отдельное наблюдение

В предыдущей статье мы довольно внимательно экспериментировали с параметрами, в том числе и с уменьшением шага обучения, и достигли точности на тестовой выборке на соответствующем датасете (MNIST) 0.9869. Не утверждаем, что это самый лучший показатель, но даже его достижение было весьма трудоемко. В этой статье мы просто брали последовательность количеств признаков с увеличением в 2 раза [128, 256, 512, 1024] и таким же образом сформированную последовательность размеров батчей [16, 32, 64,128], и просто перебирали соотношения, и таким образом достигли показателя 0.9860. Разница между 0.9860, полученными "легко и случайно", и 0.9869, полученными достаточно трудоемко, составляет сотые доли процента. С этой точки зрения вызывает отдельный интерес, насколько поднимается точность в ходе работы с зонами экстремума и схемами уменьшения шага обучения по сравнению с простым "автоматическим" перебором распространенных параметров.

Что дальше

А дальше мы рассчитываем на комментарии и рекомендации сообщества касательно рассматриваемого алгоритма и приступаем непосредственно к кодированию.