Для работы над Яндекс.Музыкой нам всегда важно помнить о разных тонкостях, которые таит в себе звук. Что такое громкость, как она меняется и от чего зависит? Как работают звуковые фильтры? Какие бывают шумы? Как меняется звук? Как люди его воспринимают.
Мы довольно много узнали обо всём этом, работая над нашим проектом, и сегодня я попробую описать на пальцах некоторые основные понятия, которые требуется знать, если вы имеете дело с цифровой обработкой звука. В этой статье нет серьёзной математики вроде быстрых преобразований Фурье и прочего — эти формулы несложно найти в сети. Я опишу суть и смысл вещей, с которыми придётся столкнуться.
Поводом для этого поста можете считать то, что мы добавили в приложения Яндекс.Музыки возможность слушать треки в высоком качестве (320kbps). А можете не считать. Итак.
Оцифровка, или Туда и обратно
Прежде всего разберёмся с тем, что такое цифровой сигнал, как он получается из аналогового и откуда собственно берётся аналоговый сигнал. Последний максимально просто можно определить как колебания напряжения, возникающие из-за колебаний мембраны в микрофоне.
Рис. 1. Осциллограмма звука
Это осциллограмма звука — так выглядит аудио сигнал. Думаю, каждый хоть раз в жизни видел подобные картинки. Для того чтобы понять, как устроен процесс преобразования аналогового сигнала в цифровой, нужно нарисовать осциллограмму звука на миллиметровой бумаге. Для каждой вертикальной линии найдем точку пересечения с осциллограммой и ближайшее целое значение по вертикальной шкале — набор таких значений и будет простейшей записью цифрового сигнала.
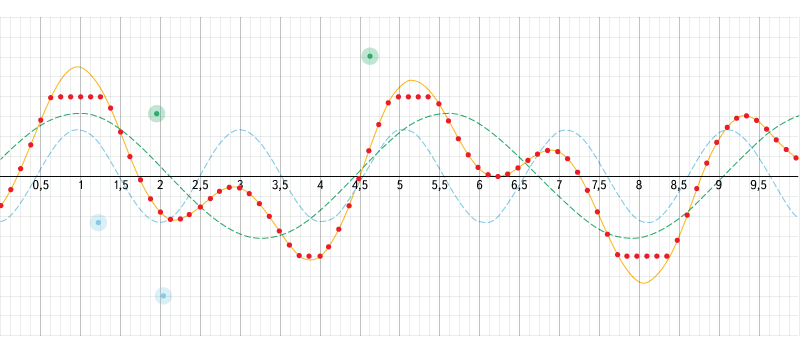
Рис. 2. Интерактивный пример сложения волн и оцифровки сигнала.
Источник: www.desmos.com/calculator/aojmanpjrl
Воспользуемся этим интерактивным примером, чтобы разобраться в том, как накладываются друг на друга волны разной частоты и как происходит оцифровка. В левом меню можно включать/выключать отображение графиков, настраивать параметры входных данных и параметры дискретизации, а можно просто двигать контрольные точки.
На аппаратном уровне это, разумеется, выглядит значительно сложнее, и в зависимости от аппаратуры сигнал может кодироваться совершенно разными способами. Самым распространённым из них является импульсно-кодовая модуляция, при которой записывается не конкретное значение уровня сигнала в каждый момент времени, а разница между текущим и предыдущим значением. Это позволяет снизить количество бит на каждый отсчёт примерно на 25%. Этот способ кодирования применяется в наиболее распространённых аудио-форматах (WAV, MP3, WMA, OGG, FLAC, APE), которые используют контейнер PCM WAV.
В реальности для создания стерео-эффекта при записи аудио чаще всего записывается не один, а сразу несколько каналов. В зависимости от используемого формата хранения они могут храниться независимо. Также уровни сигнала могут записываться как разница между уровнем основного канала и уровнем текущего.
Обратное преобразование из цифрового сигнала в аналоговый производится с помощью цифро-аналоговых преобразователей, которые могут иметь различное устройство и принципы работы. Я опущу описание этих принципов в данной статье.
Дискретизация
Как известно, цифровой сигнал — это набор значений уровня сигнала, записанный через заданные промежутки времени. Процесс преобразования непрерывного аналогового сигнала в цифровой сигнал называется дискретизацией (по времени и по уровню). Есть две основные характеристики цифрового сигнала — частота дискретизации и глубина дискретизации по уровню.
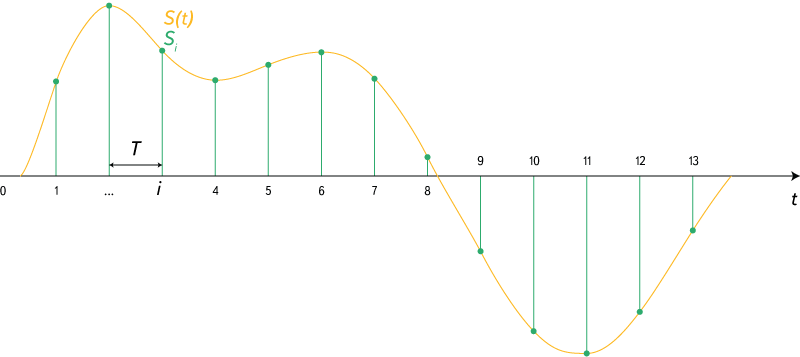
Рис. 3. Дискретизация сигнала.
Источник: https://en.wikipedia.org/wiki/Sampling_(signal_processing)
Частота дискретизации указывает на то, с какими интервалами по времени идут данные об уровне сигнала. Существует теорема Котельникова (в западной литературе её упоминают как теорему Найквиста — Шеннона, хотя встречается и название Котельникова — Шеннона), которая утверждает: для возможности точного восстановления аналогового сигнала из дискретного требуется, чтобы частота дискретизации была минимум в два раза выше, чем максимальная частота в аналоговом сигнале. Если брать примерный диапазон воспринимаемых человеком частот звука 20 Гц — 20 кГц, то оптимальная частота дискретизации (частота Найквиста) должна быть в районе 40 кГц. У стандартных аудио-CD она составляет 44.1 кГц
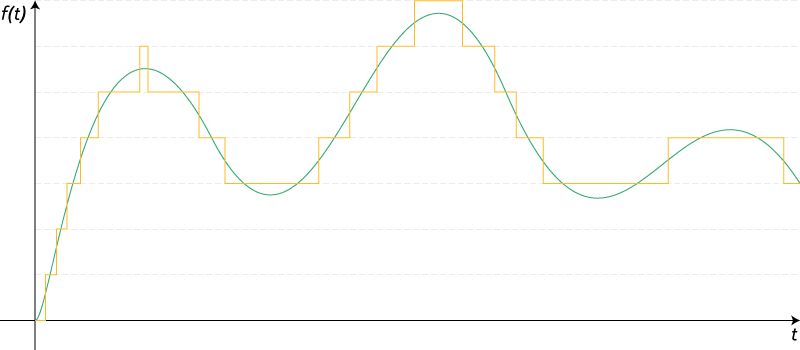
Рис. 4. Квантование сигнала.
Источник: https://ru.wikipedia.org/wiki/Квантование_(обработка сигналов)
Глубина дискретизации по уровню описывает разрядность числа, которым описывается уровень сигнала. Эта характеристика накладывает ограничение на точность записи уровня сигнала и на его минимальное значение. Стоит специально отметить, что данная характеристика не имеет отношения к громкости — она отражает точность записи сигнала. Стандартная глубина дискретизации на audio-CD — 16 бит. При этом, если не использовать специальную студийную аппаратуру, разницу в звучании большинство перестаёт замечать уже в районе 10-12 бит. Однако большая глубина дискретизации позволяет избежать появления шумов при дальнейшей обработке звука.
Шумы
В цифровом звуке можно выделить три основных источника шумов.
Джиттер
Это случайные отклонения сигнала, как правило, возникающие из-за нестабильности частоты задающего генератора или различной скорости распространения разных частотных составляющих одного сигнала. Данная проблема возникает на стадии оцифровки. Если описывать
Шум дробления
Он напрямую связан с глубиной дискретизации. Так как при оцифровке сигнала его реальные значения округляются с определённой точностью, возникают слабые шумы, связанные с её потерей. Эти шумы могут появляться не только на стадии оцифровки, но и в процессе цифровой обработки (например, если сначала уровень сигнала сильно понижается, а затем — снова повышается).
Алиасинг
При оцифровке возможна ситуация, при которой в цифровом сигнале могут появиться частотные составляющие, которых не было в оригинальном сигнале. Данная ошибка получила название Aliasing. Этот эффект напрямую связан с частотой дискретизации, а точнее — с частотой Найквиста. Проще всего понять, как это происходит, рассмотрев вот эту картинку:
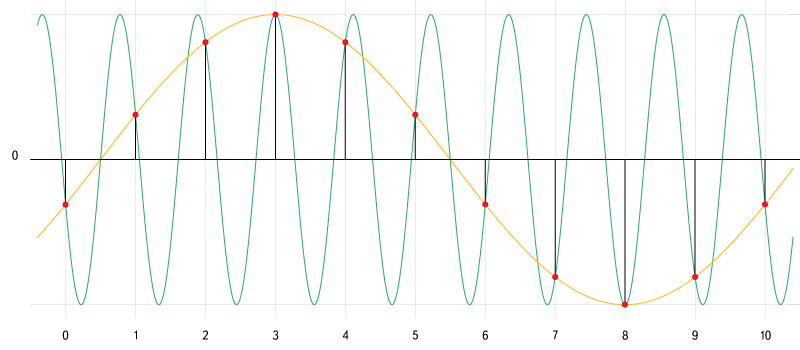
Рис. 5. Алиас. Источник: ru.wikipedia.org/wiki/Алиасинг
Зелёным показана частотная составляющая, частота которой выше частоты Найквиста. При оцифровке такой частотной составляющей не удаётся записать достаточно данных для её корректного описания. В результате при воспроизведении получается совершенно другой сигнал — жёлтая кривая.
Уровень сигнала
Для начала стоит сразу понять, что когда речь идёт о цифровом сигнале, то можно говорить только об относительном уровне сигнала. Абсолютный зависит в первую очередь от воспроизводящей аппаратуры и прямо пропорционален относительному. При расчётах относительных уровней сигнала принято использовать децибелы. При этом за точку отсчёта берётся сигнал с максимально возможной амплитудой при заданной глубине дискретизации. Этот уровень указывается как 0 dBFS (dB — децибел, FS = Full Scale — полная шкала). Более низкие уровни сигнала указываются как -1 dBFS, -2 dBFS и т.д. Вполне очевидно, что более высоких уровней просто не бывает (мы изначально берём максимально возможный уровень).
Поначалу бывает тяжело разобраться с тем, как соотносятся децибелы и реальный уровень сигнала. На самом деле всё просто. Каждые ~6 dB (точнее 20 log(2) ~ 6.02 dB) указывают на изменение уровня сигнала в два раза. То есть, когда мы говорим о сигнале с уровнем -12 dBFS, понимаем, что это сигнал, уровень которого в четыре раза меньше максимального, а -18 dBFS — в восемь, и так далее. Если посмотреть на определение децибела, в нём указывается значение 10 log(a/a0) — тогда откуда берётся 20? Всё дело в том, что децибел — это логарифм отношения двух одноимённых энергетических величин, умноженный на 10. Амплитуда же не является энергетической величиной, следовательно её нужно перевести в подходящую величину. Мощность, которую переносят волны с разными амплитудами, пропорциональна квадрату амплитуды. Следовательно для амплитуды (если все прочие условия, кроме амплитуды принять неизменными) формулу можно записать как
N.B. Стоит упомянуть, что логарифм в данном случае берётся десятичный, в то время как большинство библиотек под функцией с названием log подразумевает натуральный логарифм.
При различной глубине дискретизации уровень сигнала по этой шкале изменяться не будет. Сигнал с уровнем -6 dBFS останется сигналом с уровнем -6 dBFS. Но всё же одна характеристика изменится — динамический диапазон. Динамический диапазон сигнала — это разница между его минимальным и максимальным значением. Он рассчитывается по формуле
Восприятие
Когда мы говорим о восприятии звука человеком, следует сначала разобраться, каким образом люди воспринимают звук. Очевидно, что мы слышим с помощью ушей. Звуковые волны взаимодействуют с барабанной перепонкой, смещая её. Вибрации передаются во внутреннее ухо, где их улавливают рецепторы. То, насколько смещается барабанная перепонка, зависит от такой характеристики, как звуковое давление. При этом воспринимаемая громкость зависит от звукового давления не напрямую, а логарифмически. Поэтому при изменении громкости принято использовать относительную шкалу SPL (уровень звукового давления), значения которой указываются всё в тех же децибелах. Стоит также заметить, что воспринимаемая громкость звука зависит не только от уровня звукового давления, но ещё и от частоты звука:
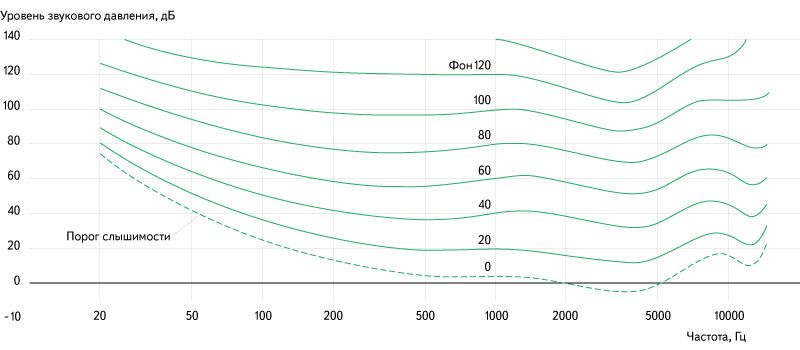
Рис. 6. Зависимость воспринимаемой громкости от частоты и амплитуды звука.
Источник: ru.wikipedia.org/wiki/Громкость_звука
Громкость
Простейшим примером обработки звука является изменение его громкости. При этом происходит просто умножение уровня сигнала на некоторое фиксированное значение. Однако даже в таком простом деле, как регулировка громкости, есть один подводный камень. Как я уже отметил ранее, воспринимаемая громкость зависит от логарифма звукового давления, а это значит, что использование линейной шкалы громкости оказывается не очень эффективным. При линейной шкале громкости возникает сразу две проблемы — для ощутимого изменения громкости, когда ползунок находится выше середины шкалы приходится достаточно далеко его сдвигать, при этом ближе к самому низу шкалы сдвиг меньше, чем на толщину волоса, может изменить громкость в два раза (думаю, с этим каждый сталкивался). Для решения данной проблемы используется логарифмическая шкала громкости. При этом на всей её длине передвижение ползунка на фиксированное расстояние меняет громкость в одинаковое количество раз. В профессиональной записывающей и обрабатывающей аппаратуре, как правило, используется именно логарифмическая шкала громкости.
Математика
Тут я, пожалуй, немного вернусь к математике, потому что реализация логарифмической шкалы оказывается не такой простой и очевидной вещью для многих, а найти в интернете данную формулу не так просто, как хотелось бы. Заодно покажу, как просто переводить значения громкости в dBFS и обратно. Для дальнейших объяснений это будет полезным.
// Минимальное значение громкости - на этом уровне идёт отключение звука
var EPSILON = 0.001;
// Коэффициент для преобразований в dBFS и обратно
var DBFS_COEF = 20 / Math.log(10);
// По положению на шкале вычисляет громкость
var volumeToExponent = function(value) {
var volume = Math.pow(EPSILON, 1 - value);
return volume > EPSILON ? volume : 0;
};
// По значению громкости вычисляет положение на шкале
var volumeFromExponent = function(volume) {
return 1 - Math.log(Math.max(volume, EPSILON)) / Math.log(EPSILON);
};
// Перевод значения громкости в dBFS
var volumeToDBFS = function(volume) {
return Math.log(volume) * DBFS_COEF;
};
// Перевод значения dBFS в громкость
var volumeFromDBFS = function(dbfs) {
return Math.exp(dbfs / DBFS_COEF);
}
Цифровая обработка
Теперь вернёмся к тому, что мы имеем цифровой, а не аналоговый сигнал. У цифрового сигнала есть две особенности, которые стоит учитывать при работе с громкостью:
- точность, с которой указывается уровень сигнала, ограничена (причём достаточно сильно. 16 бит — это в 2 раза меньше, чем используется для стандартного числа с плавающей точкой);
- у сигнала есть верхняя граница уровня, за которую он не может выйти.
Из того, что уровень сигнала имеет ограничение точности, следует две вещи:
- уровень шумов дробления возрастает при увеличении громкости. Для малых изменений обычно это не очень критично, так как изначальный уровень шума значительно тише ощутимого, и его можно безопасно поднимать в 4-8 раз (например, применять эквалайзер с ограничением шкалы в ±12dB);
- не стоит сначала сильно понижать уровень сигнала, а затем сильно его повышать — при этом могут появиться новые шумы дробления, которых изначально не было.
Из того, что сигнал имеет верхнее ограничение уровня, следует, что нельзя безопасно увеличивать громкость выше единицы. При этом пики, которые окажутся выше границы, будут «срезаны» и произойдёт потеря данных.
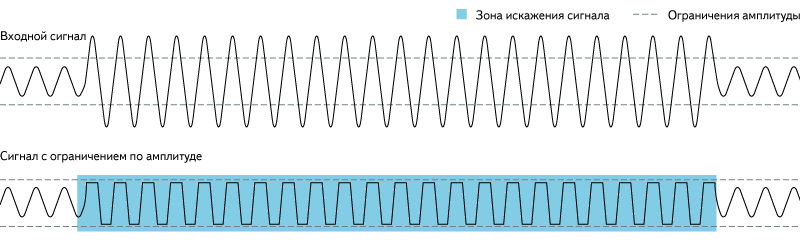
Рис. 7. Клиппинг.
Источник: https://en.wikipedia.org/wiki/Clipping_(audio)
На практике всё это означает, что стандартные для Audio-CD параметры дискретизации (16 бит, 44,1 кГц) не позволяют производить качественную обработку звука, потому что имеют очень малую избыточность. Для этих целей лучше использовать более избыточные форматы. Однако стоит учитывать, что общий размер файла пропорционален параметрам дискретизации, поэтому выдача таких файлов для он-лайн воспроизведения — не лучшая идея.
Измерение громкости
Для того чтобы сравнивать громкость двух разных сигналов, её для начала нужно как-то измерить. Существует по меньшей мере три метрики для измерения громкости сигналов — максимальное пиковое значение, усреднённое значение уровня сигнала и метрика ReplayGain.
Максимальное пиковое значение достаточно слабая метрика для оценки громкости. Она никак не учитывает общий уровень громкости — например, если записать грозу, то большую часть времени на записи будет тихо шелестеть дождь и лишь пару раз прогремит гром. Максимальное пиковое значение уровня сигнала у такой записи будет довольно высоким, но большая часть записи будет иметь весьма низкий уровень сигнала. Однако эта метрика всё равно является полезной — она позволяет вычислить максимальное усиление, которое можно применить к записи, при котором не будет потерь данных из-за «обрезания» пиков.
Усреднённое значение уровня сигнала — более полезная метрика и легко вычислимая, но всё же имеет существенные недостатки, связанные с тем, как мы воспринимаем звук. Визг циркулярной пилы и рокот водопада, записанные с одинаковым средним уровнем сигнала, будут восприниматься совершенно по-разному.
ReplayGain наиболее точно передает воспринимаемый уровень громкости записи и учитывает физиологические и психические особенности восприятия звука. Для промышленного выпуска записей многие звукозаписывающие студии используют именно её, также она поддерживается большинством популярных медиа-плееров. (Русская статья на WIKI содержит много неточностей и фактически не корректно описывает саму суть технологии)
Нормализация громкости
Если мы можем измерять громкость различных записей, мы можем её нормализовать. Идея нормализации состоит в том, чтобы привести разные звуки к одинаковому уровню воспринимаемой громкости. Для этого используется несколько различных подходов. Как правило, громкость стараются максимизировать, но это не всегда возможно из-за ограничений максимального уровня сигнала. Поэтому обычно берётся некоторое значение немного меньше максимума (например -14 dBFS), к которому пытаются привести все сигналы.
Иногда нормализацию громкости производят в рамках одной записи — при этом различные части записи усиливают на разные величины, чтобы их воспринимаемая громкость была одинаковой. Такой подход очень часто применяется в компьютерных видео-плеерах — звуковая дорожка многих фильмов может содержать участки с очень сильно отличающейся громкостью. В такой ситуации возникают проблемы при просмотре фильмов без наушников в позднее время — при громкости, на которой нормально слышен шёпот главных героев, выстрелы способны перебудить соседей. А на громкости, при которой выстрелы не бьют по ушам, шёпот становится вообще неразличим. При внутри-трековой нормализации громкости плеер автоматически увеличивает громкость на тихих участках и понижает на громких. Однако этот подход создаёт ощутимые артефакты воспроизведения при резких переходах между тихим и громким звуком, а также порой завышает громкость некоторых звуков, которые по задумке должны быть фоновыми и еле различимыми.
Также внутреннюю нормализацию порой производят, чтобы повысить общую громкость треков. Это называется нормализацией с компрессией. При этом подходе среднее значение уровня сигнала максимизируется за счёт усиления всего сигнала на заданную величину. Те участки, которые должны были быть подвергнуты «обрезанию», из-за превышения максимального уровня усиливаются на меньшую величину, позволяя избежать этого. Этот способ увеличения громкости значительно снижает качество звучания трека, но, тем не менее, многие звукозаписывающие студии не брезгуют его применять.
Фильтрация
Я не стану описывать совсем все аудио-фильтры, ограничусь только стандартными, которые присутствуют в Web Audio API. Самым простым и распространённым из них является биквадратный фильтр (BiquadFilterNode) — это активный фильтр второго порядка с бесконечной импульсной характеристикой, который может воспроизводить достаточно большое количество эффектов. Принцип работы этого фильтра основан на использовании двух буферов, каждый с двумя отсчётами. Один буфер содержит два последних отсчёта во входном сигнале, другой — два последних отсчёта в выходном сигнале. Результирующее значение получается с помощью суммирования пяти значений: текущего отсчёта и отсчётов из обоих буферов перемноженных на заранее вычисленные коэффициенты. Коэффициенты данного фильтра задаются не напрямую, а вычисляются из параметров частоты, добротности (Q) и усиления.
Все графики ниже отображают диапазон частот от 20 Гц до 20000 Гц. Горизонтальная ось отображает частоту, по ней применяется логарифмический масштаб, вертикальная — магнитуду (жёлтый график) от 0 до 2, или фазовый сдвиг (зелёный график) от -Pi до Pi. Частота всех фильтров (632 Гц) отмечена красной чертой на графике.
Lowpass
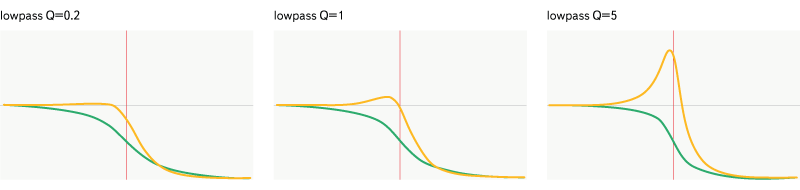
Рис. 8. Фильтр lowpass
Пропускает только частоты ниже заданной частоты. Фильтр задаётся частотой и добротностью.
Highpass
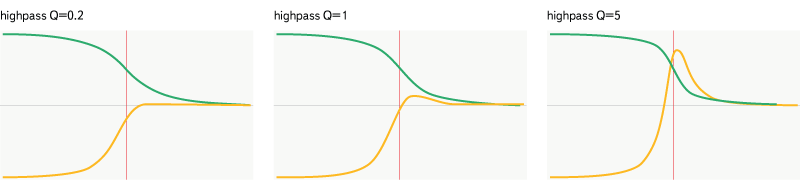
Рис. 9. Фильтр highpass
Действует аналогично lowpass, за исключением того, что он пропускает частоты выше заданной, а не ниже.
Bandpass
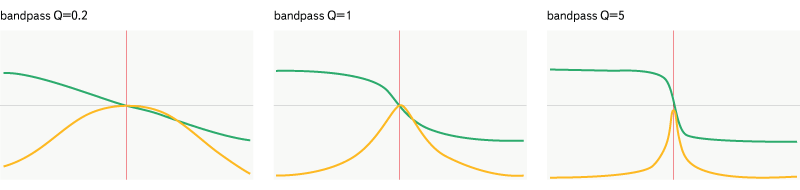
Рис. 10. Фильтр bandpass
Этот фильтр более избирателен — он пропускает только определённую полосу частот.
Notch
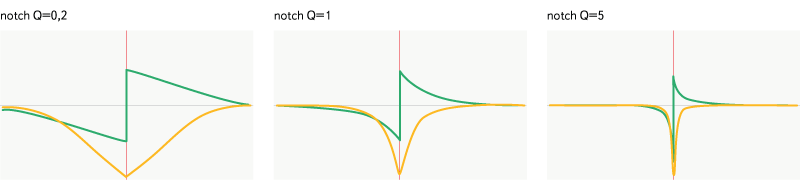
Рис. 11. Фильтр notch
Является противоположностью bandpass — пропускает все частоты вне заданной полосы. Стоит, однако, отметить разность в графиках затухания воздействия и в фазовых характеристиках данных фильтров.
Lowshelf
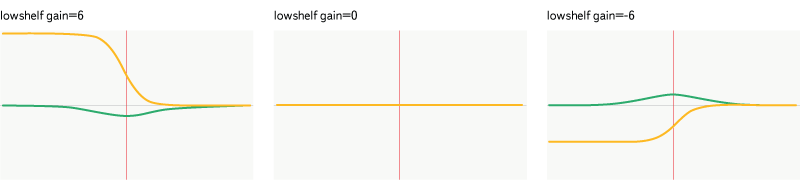
Рис. 12. Фильтр lowshelf
Является более «умной» версией highpass — усиливает или ослабляет частоты ниже заданной, частоты выше пропускает без изменений. Фильтр задаётся частотой и усилением.
Highshelf
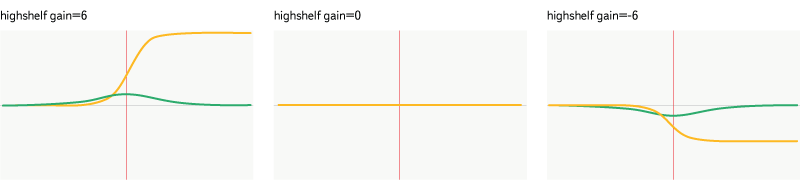
Рис. 13. Фильтр highshelf
Более умная версия lowpass — усиливает или ослабляет частоты выше заданной, частоты ниже пропускает без изменений.
Peaking
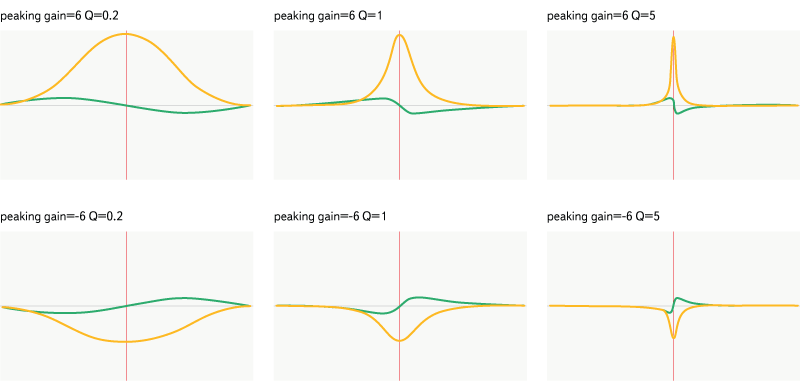
Рис. 14. Фильтр peaking
Это уже более «умная» версия notch — он усиливает или ослабляет частоты в заданном диапазоне и пропускает остальные частоты без изменений. Фильтр задаётся частотой, усилением и добротностью.
Фильтр allpass
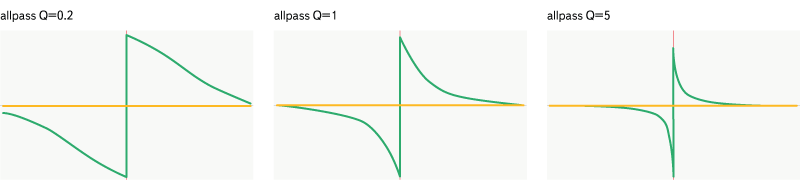
Рис. 15. Фильтр allpass
Allpass отличается ото всех остальных — он не меняет амплитудные характеристики сигнала, вместо чего делает фазовый сдвиг заданных частот. Фильтр задаётся частотой и добротностью.
Фильтр WaveShaperNode
Вейвшейпер (en) применяется для формирования сложных эффектов звуковых искажений, в частности с помощью него можно реализовать эффекты «дисторшна», «овердрайва» и «фузза». Данный фильтр применяет к входному сигналу специальную формирующую функцию. Принципы построения подобных функций довольно сложные и тянут на отдельную статью, поэтому я опущу их описание.
Фильтр ConvolverNode
Фильтр, производящий линейную свёртку входного сигнала с аудио-буфером, задающим некую импульсную характеристику. Импульсная характеристика — это ответ некой системы на единичный импульс. Простым языком это можно назвать «фотографией» звука. Если реальная фотография содержит информацию о световых волнах, о том, насколько они отражаются, поглощаются и взаимодействуют, то импульсная характеристика содержит аналогичную информацию о звуковых волнах. Свёртка аудио-потока с подобной «фотографией» как бы накладывает эффекты окружения, в котором была сняла импульсная характеристика на входной сигнал.
Для работы данного фильтра требуется разложение сигнала на частотные составляющие. Это разложение производится с помощью быстрого преобразования Фурье (к сожалению, в русскоязычной Википедии совершенно несодержательная статья, написанная, судя по всему, для людей, которые и так знают, что такое БПФ и сами могут написать такую же несодержательную статью). Как я уже говорил во вступлении, не стану приводить в данной статье математику БПФ, однако не упомянуть краеугольный алгоритм для цифровой обработки сигналов было бы неправильно.
Данный фильтр реализует эффект реверберации. Существует множество библиотек готовых аудио-буферов для данного фильтра, которые реализуют различные эффекты (1, 2), подобные библиотеки хорошо находятся по запросу [impulse response mp3].
Материалы
- О понятии громкости в цифровом представлении звука и о методах её повышения
- Звук
- Амплитуда
- Частота
- Цифровой сигнал
- Аналоговый сигнал
- Цифровая обработка сигналов
- Интерактивный пример сложения волн и оцифровки сигнала
- Аналогово-цифровой преобразователь
- Цифро-аналоговый преобразователь
- Импульсно-кодовая модуляция
- Формат PCM WAV
- Сэмплирование (en)
- Частота дискретизации
- Теорема Котельникова
- Частота Найквиста
- Глубина дискретизации
- Alias
- Децибел
- Строение уха
- Звуковое давление
- Воспринимаемая громкость
- Клиппинг
- ReplayGain описание
- ReplayGain спецификация
- Быстрое преобразование Фурье, вики, wiki
- Импульсная характеристика
- Фазо-частотная характеристика
- Амплитудо-частотная характеристика
- Фильтр с бесконечной импульсной характеристикой
- Фильтр с конечной импульсной характеристикой
- Биквадратный фильтр (en)
- BiquadFilterNode
- HTML5 Audio W3C
- Web Audio API
- Вейвшейпер
- Дисторшн
- Овердрайв
- Фузз
- Реверберации
- Свёртка
- Эквалайзер
Большое спасибо моим коллегам, которые помогали собирать материалы для этой статьи и давали полезные советы.
Отдельное спасибо Тарасу Audiophile Ковриженко за описание алгоритмов нормализации и максимизации громкости и Сергею forgotten Константинову за большое количество пояснений и советов по данной статье.
UPD. Поправил раздел про фильтрацию и добавил ссылки по разным типам фильтров. Спасибо deniskreshikhin и merlin-vrn за то, что обратили внимание.
Комментарии (44)
deniskreshikhin
12.11.2015 22:22+1Есть два существенных замечания.
Как известно, цифровой сигнал — это набор значений уровня сигнала, записанный через заданные промежутки времени. Процесс преобразования непрерывного аналогового сигнала в дискретный цифровой сигнал называется дискретизацией. Есть две основные характеристики цифрового сигнала — частота дискретизации и глубина дискретизации по уровню.
Во-первых, тут присутствует путаница в терминологии.
Дискретный по времени сигнал или кратко просто дискретный (он же импульсный, квантованый по времени) это отдельный вид сигналов. Как раз для него и верна теорема Котельникова.
Квантованный сигнал, он же квантованный по уровню — другой вид сигналов.
А квантованный дискретный сигнал уже называется цифровым. Для него теорема Котельникова верна лишь приближенно.
Т.е. термин «дискретный цифровой сигнал» одновременно и не верен, и тавтологичен.
Во-вторых, пассивные фильтры, или как вы их назвали «глушащие» не могут иметь коэффициент усиления выше 1. Т.к. они могут только подавлять некоторые частоты, но не усиливать. Глядя же на эти графики можно подумать что происходит усиление:
Во всяком случае не понятно что означают оси, очевидно не уровень 0dB. Но тогда что?
gheljenor
12.11.2015 22:42+1Да, по первому пункту согласен, скорее всего в процессе редактирования напортачил, сейчас поправлю.
Насчёт второго пункта — серая полоса на графика показывает сигнал с уровнем 1. И я тоже считал, что эти фильтры не должны вызывать усиления сигнала, однако именно такой график получается, если брать информацию из BiquadFilterNode#getFrequencyResponse. Либо это ошибка в реализации данной функции, либо сам фильтр действительно так устроен, тестов пока не проводил. Вообще этот график сильно похож на график групповой задержки для фильтра Баттерворта (https://ru.wikipedia.org/wiki/%D0%A4%D0%B8%D0%BB%D1%8C%D1%82%D1%80_%D0%91%D0%B0%D1%82%D1%82%D0%B5%D1%80%D0%B2%D0%BE%D1%80%D1%82%D0%B0)gheljenor
12.11.2015 23:31Используя webaudioplayground.appspot.com (спасибо dtestyk) Воспроизвёл поведение данного фильтра:
Создаём такую схему: Oscillator node -> Biquad filter (lowpass, Q=15, freq=5000) -> Analyzer -> выход
Запускаем воспроизведение в oscilator'е и меняем частоту. В районе 5000 Hz отчётливо слышно и видно резкое усиление звука.
Так что данные графики отображают действительную картину того, как работает фильтр lowpass в web audio api.deniskreshikhin
13.11.2015 00:28Ага, я тоже уже посмотрел спецификацию и исходники. В общем, эти типы фильтров которые реализованы в Web Audio API с помощью биквадратного фильтра все являются усиливающими, т.к. нормированы к нулевой частоте, а не резонансу как это должно быть в «глушащих фильтрах».
Строго говоря, в спецификации и нет такого деления на «глушащие» и «усиливающие», типы же фильтров в спецификации просто отражают способ задания исходных параметров.
Кстати, не обратил внимания, но еще есть одна неточность.Принцип работы всех перечисленных фильтров основан на разложении сигнала на различные частотные составляющие — это позволяет производить манипуляции не только над общей громкость, но и над отдельными наборами частот. Разложение сигнала на частотные составляющие производится с помощью быстрого преобразования Фурье
Это не правда.
Цифровые фильтры не требуют расчета БПФ, в данном случае биквадратный фильтр использует задержку 2 отсчетов от аргумента и двух отсчетов от функции. Т.е. получается около 5 умножений на каждый отсчет, это намного выгоднее чем БПФ, во первых т.к. N*log(N) это будет больше чем 5*N при достаточно больших N. Во-вторых БПФ создает огромную задержку, а задержка на 2 отсчета вообще не заметная для слуха.
Можете кстати посмотреть как это реализуется, алгоритм довольно простой:
while (n--) { // FIXME: this can be optimized by pipelining the multiply adds... float x = *sourceP++; float y = b0*x + b1*x1 + b2*x2 - a1*y1 - a2*y2; *destP++ = y; // Update state variables x2 = x1; x1 = x; y2 = y1; y1 = y; }
А вот задать коэффициенты уже не так просто:
// Compute biquad coefficients for lowpass filter resonance = std::max(0.0, resonance); // can't go negative double g = pow(10.0, 0.05 * resonance); double d = sqrt((4 - sqrt(16 - 16 / (g * g))) / 2); double theta = piDouble * cutoff; double sn = 0.5 * d * sin(theta); double beta = 0.5 * (1 - sn) / (1 + sn); double gamma = (0.5 + beta) * cos(theta); double alpha = 0.25 * (0.5 + beta - gamma); double b0 = 2 * alpha; double b1 = 2 * 2 * alpha; double b2 = 2 * alpha; double a1 = 2 * -gamma; double a2 = 2 * beta;
github.com/WebKit/webkit/blob/20f480a542d431da0d4ffe84347b498bdd614bb8/Source/WebCore/platform/audio/Biquad.cpp
gheljenor
12.11.2015 22:59-1И да, стоит добавить, что если говорить о цифровом сигнале, что точно восстановить из него аналоговый может не получиться даже, если частота дискретизации выше частоты Найквиста, т.к. есть ещё искажения сигнала связанные с его квантованием по уровню. Однако, нижняя граница частоты дискретизации всё равно не меняется.
deniskreshikhin
13.11.2015 01:14>> Однако, нижняя граница частоты дискретизации всё равно не меняется.
Ну это немного не правда) Нижняя частота не меняется при оцифровке способом, который описан в теореме Котельникова. Но есть способы оцифровки как с меньшей частотой (представление Хургина-Яковлева), так и с большей — дельта-модуляци и т.п.
Т.е. теорема Котельникова не является каким-то универсумом, но тем не менее она применима, с некоторыми оговорками, к тому что мы имеем на практике когда оцифровываем сигнал равными интервалами по уровням, т.н. используя импульсно-кодовую модуляцию (PCM). Т.е. то о чем речь идет в статье.
А вообще у теоремы Котельникова много недостатков:
— требуется бесконечное количество отсчетов,
— требуется бесконечная задержка для восстановления сигнала,
— требуется бесконечно большое количество уровней квантования,
— требуется сигналы с бесконечной длительностью (т.к. только такие имеют ограниченную частоту).
Но все-таки с некоторыми допустимыми ошибками она работает)
forgotten
13.11.2015 09:52+2Да, но нет.
Можно взять конечный по времени сигнал, периодически его продолжить и применить теорему Котельникова. (Правда, придётся работать в обобщённых функциях.) Это снимет все перечисленные недостатки (бесконечное число отсчетов, бесконечная задержка, etc — отсчёты-то повторяются). Но «работать» от этого теорема Котельникова не начнёт, поскольку восстановить по ней сигнал может только математик формулами на бумаге, а реальный ЦАП ничего и близко похожего на процедуру восстановления сигнала по Котельникову выдать не может.
Подумываю написать статью «Легенды и мифы о теореме Котельникова».
merlin-vrn
13.11.2015 10:19Ну как, «ничего похожего». Ну да, ? x[i] sinc(t) в реальности использовать невозможно. Но используют же «обрезанную половинку sinc» — она похожа до некоторой степени.
forgotten
13.11.2015 10:53В реальности на каждый отсчёт нужно брать по синусоиде, притом с точностью до 6-го знака после запятой. Даже если брать окно 0.05 секунды (исходя из минимальной слышимой человеком частоты 20 Гц), потребуется сложить более 2000 синусоид. Чего-то я не видал таких ЦАП.
diakin
14.11.2015 18:36Теорема Котельникова — это математическая теорема ) У нее не может быть «недостатков», поскольку она математически верна (строго доказана). Проблемы применение мат аппарата к решению каких-то прикладных задач — это проблемы самих прикладных задач. Поэтому говорить, что " у теоремы есть определенные недостатки" или «она работает, хотя и плоховато» как-то несколько неправильно ).
deniskreshikhin
14.11.2015 20:28+1>> У нее не может быть «недостатков», поскольку она математически верна (строго доказана).
Математика это довольно практическая наука. Есть теоремы (и теории) которые понятны, многое объясняют и легко применяются. А есть которые непонятны, запутывают и трудны в применении.
Теорема Котельникова ближе ко вторым, т.к. порождает очень много ошибок и непонимания.
Грубо говоря, задача дискретизации в обобщенном виде задача звучит так: Если имеется некоторая функция X из пространства L2(пространство квадратично интегрируемых функций), то как построить некоторый оператор A которые бы ставил ей в соответствие вектор Y из l2 (пространство квадратично суммируемых векторов). А то что эти пространства изоморфны доказал еще Гильберт.
По-сути теорема Котельникова решает эту проблему так: если рассмотреть из всего пространства L2 только подпространство функций с ограниченным спектром (т.н. пространства Пели-Винера), то оператор A представляет собой разложение по дельта-функциям выбранным с некоторым периодом. Этот период и определяет частоту дискретизации, т.н. частота Найквиста.
Т.е. в теореме Котельникова решается намного более узкая задача, которая немного не соответствует практике, плюс навязывается метод дискретизации в виде ИКМ. Теперь этот метод дискретизации всеми воспринимается как единственно возможный, а частота Найквиста как что-то непоколебимое. Но это не соответствует действительности, можно захватывать и более обширный класс функций, и не обязательно равными интервалами, и не обязательно с такой частотой.
Поэтому, и говорят про недостатки теоремы.
Насчет «работает» и «не работает», то в математике это сплошь и рядом. Интеграл Римана не работает со многими функциями, а интеграл Лебега вполне работает. Если вам не нравится слово «работает», замените на слово «применимо».
Т.е. можно перефразировать так:
>> Но все-таки с некоторыми допустимыми ошибками она применима)merlin-vrn
15.11.2015 09:12Но все-таки с некоторыми допустимыми ошибками она применима
В подобном случае в математике принято оценивать эти самые ошибки.deniskreshikhin
15.11.2015 11:55Безусловно, но в математике понятие ошибки может подразумевать все что угодно. Оценка ошибок, это то чем должен заниматься инженер при проектировании на основе априорной информации. Без учета ошибок нельзя даже двух чисел корректно сложить в общем случае.
dtestyk
12.11.2015 23:15+1может кому будет полезно:
toxicdump.org/stuff/FourierToy.swf визуализация синусоид
bfxr.net генерация с множеством параметров
text programming sound synthesis:
wavepot.com
studio.substack.net
wurstcaptures.untergrund.net/music
visual block playground:
webaudioplayground.appspot.com
app.hya.io
языки программирования звука:
pure data графический
ChucK текстовый
foxyrus
12.11.2015 23:17+10Еще бы вы в яндекс радио нормализовали уровень громкости рекламы.
gevak
13.11.2015 12:01+1работаем над этим
TimsTims
13.11.2015 12:27Раз пошла такая пьянка про хотелки в Яндекс.музыке, то сделайте пожалуйста кнопку «Избранные» жанры, доступные со стартового.
Чаще всего слушаю «Энергичное» — оно как-то больше всего подходит, но он постоянно в самом конце длинного списка «Настроение», и очень редко, когда программа предлагает послушать этот жанр с первой страницы… А так — добавил в избранное и всегда где-то в быстром запуске.
2) Ну и дополню — я забиндил вашу прогу как программу по умолчанию в качестве музыки в Android'е, стоп/пауза и Next работают, а вот «холодный старт» нет. Т.е. нельзя просто с гарнитуры нажать «Play» и начать слушать музыку — приложение Стартует, но просит выбрать жанр. Т.е. просто начать слушать с гарнитуры нельзя.
3) Очень мало песен в стиле «Русский рэп». Иногда настроение такое, что хочется послушать жесткого гопо-рэпа, а там… всякие сопливые «тимати» и ко)) и почти нет Касты. АК47, Centr итд…
pwl
13.11.2015 05:00Какая куча ошибок…
Начнем с простого:
Самым распространённым из них является импульсно-кодовая модуляция,
ага. PCM.
при которой записывается не конкретное значение уровня сигнала в каждый момент времени, а разница между текущим и предыдущим значением. Это позволяет снизить количество бит на каждый отсчёт примерно на 25%.
А вот это уже DPCM.
Этот способ кодирования применяется в наиболее распространённых аудио-форматах (WAV, MP3, WMA, OGG, FLAC, APE), которые используют контейнер PCM WAV.
Здесь-же прекрасно почти всё…
PCM в mp3 ??? Это как?
WAV, WMA, OGG — это не форматы. Это контейнеры. Тот-же WAV может содержать внутри как PCM, так и mp3
А вот PCM WAV это уже конкретный формат, а никак не контейнер…forgotten
13.11.2015 10:58+1mp3 и прочие кодеки занимаются тем, что перекодируют PCM WAV во что-то более компактное. Поэтому формулировка «все эти кодеки используют PCM WAV» правильная, хоть и странная. Именно что «используют».
Fanamura
13.11.2015 10:13-1А когда в Яндекс.Музыке можно будет ожидать «похожее по исполнеНЕНИЮ». Чтобы можно было начать слушать любой трек и дальше слушать любых исполнителей схожих по звучанию? Даже если слушать радио по определенному жанру, там ну очень все разнообразное и такое ощущение, что просто собираются исполнители у которых тег = жанру, даже если это фактически не так. Искать не по исполнителю, не жанру, а именно звучанию. Или это какой-то космос в плане технологий и «харя треснет»?)
AnimaLocus
13.11.2015 10:57Космос. Лучшее что можно предложить это релейтед с ластфм, ну и у них база самая большая для построения подобного (у айтюнса конечно больше, но они особо не занимаются этим :)).
Certik
13.11.2015 18:57Релейтед с ластфм работает примерно так же хорошо как «с этим товаром часто покупают». То есть чуть лучше, чем никак.
Теоретически, должно быть вполне возможно машинно проанализировать музыку по каким-то ключевым параметрам. А если к этому добавить тегирование не только по жанру, но и, например, по «составу» (хотя бы на уровне вокал есть/нет, ключевой инструмент, тип состава (соло/дуэт/группа/камерный оркестр/симфонический оркестр)), то можно выдавать действительно похожую музыку. Конечно, тегирование по составу машина сделать вряд ли сможет, но так и жанры пока что «руками» определяются.
dtestyk
13.11.2015 11:29существуют высокоуровневые признаки:
- energy
- dancibility
- hotttnesss
- duration
- speechiness
- acousticness
- liveness
- tempo
- ...
merlin-vrn
13.11.2015 14:49dancibility
Пожалуй, самый спорный признак. А именно, послушайте музыку (но не смотрите постановку) из танца Монтекки и Капулетти из балета «Ромэо и Джульетта» С. Прокофьева. Знаменитая музыкальная тема, мощная и энергичная. dancibility? Ау, это балет, оно делалось для танца.
И теперь если вы не видели балет, вы не догадаетесь даже примерно, как выглядит этот танец.
merlin-vrn
13.11.2015 11:17Сумбурная и непоследовательная статья. Как и большинство подобных статей. Вот характерные признаки:
— пишут про теорему Котельникова: можно восстановить по отсчётам. И всё. Как потом восстановить — ни слова, и далёкие от математики читатели себе выдумывают «лесенку», потом им она не нравится, начинается — линейная интерполяция, квадратичная, кубическая… А потом видим утверждения (было и прямо на Хабре), что при восстановлении из отсчётов -1, 0, +1, 0, -1, 0, +1, 0,… в результате сигнал получается треугольный. Ну или что восстановленный по отсчётам 0, 0, 1, 1, 0, 0, 1, 1,… сигнал окажется меандром. А это совершенно не так, если мы говорим о теореме, потому, что как треугольник, так и меандр заведомо не являются ограниченными по частоте, не удовлетворяют её условию, поэтому не могли быть теми функциями, из которых мы получили отсчёты, и следовательно не могут получиться и в резульате восстановления по этим отсчётам.
А ведь достаточно было написать формулу для восстановления: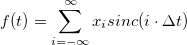
и всё, сразу видно: отсчётов нам нужно бесконечное количество, для восстановления почти в каждой точке нужно использовать сразу все отсчёты, а восстановленная функция в любом случае будет гладкой, не будет содержать никаких «острых углов». А если кто не знает, sinc(x)=sin(x)/x. То есть, как обычно, это математическая идеализация, непосредственно не применимая на практике, и для использования нужно строить с её помощью какие-то практически реализуемые конструкции.
— пишут про преобразование Фурье (даже не упоминая, что имеют ввиду именно дискретное преобразование). А то и сразу про БПФ, вроде как про серебрянную пулю (опять, имея ввижу исключительно алгоритм Cooley–Tukey и его требование, чтобы число отсчётов было степенью 2, хотя это — не единственный алгоритм БПФ, и у других такого жёсткого требования нет). А иногда речь на самом деле идёт про косинусное преобразование (частный случай, применяется в JPEG и т. д.).
И всё, что говорится про него — «разделяет сигнал на частоты». В чём заключается преобразование, что получается в результате, про оконирование — ни слова. А тут опять дьявол — в деталях. Формулы-то преобразования туда и обратно несложные, казалось бы, почему бы не выписать их? И сразу же станет видно, что результат преобразования — набор комплексных чисел и не всё там так просто.
— пишут про фильтры. Тут вообще атас, утверждения, что обрезные, шельфовые, полосовые фильтры делаются с помощью преобразования Фурье. Простой же вопрос — откуда тогда там появляется переменнй сдвиг фаз, если мы в образе были вольные его не вносить — не возникает ни у написателя статьи, ни у аудитории.
Ответ на этот вопрос очень прост: никто не реализует фильтр с помощью преобразования Фурье. Есть такие штуки — фильтры КИХ и фильтры БИХ, у каждого из них свои особенности, вот их-то все и используют. Сдвиг фаз как раз является следствием применения таких фильтров.
Куда было бы от вашей статьи больше пользы, если бы вы про Web Audio API рассказали подробнее, а не повторяли плохое изложение основ цифрового звука.gheljenor
13.11.2015 12:06Насчёт «достаточно было написать формулу для восстановления» — совершенно не достаточно. Сколько бы человек её поняло? Для большинства это просто набор математических символов. Я специально исключил практически всю математику из статьи и даже не пытался описывать некоторые детали — это сделало бы статью в разы больше и непонятнее. Плюс к тому я вроде нигде не забыл оставить ссылки на более содержательные и подробные статьи по каждой сложной теме.
Насчёт «повторения плохого изложения» — если бы было что повторять, этой статьи вообще бы не было. Но чтобы собрать материалы у меня ушло около недели поисков по интернету и вдумчивого чтения далеко не адаптированного для обывателей материала.
Насчёт фильтров каюсь — сам не разобрался до конца в теме, перепишу этот блок. Спасибо за пояснение про то откуда берётся фазовый сдвиг.
Про Web Audio API скорее всего будет отдельная статья.merlin-vrn
13.11.2015 14:42Может, я неправ, но подобных статей даже на хабре было несколько. А уж за пределами хабра…
Мне казалось, пользователи Хабра способны, видя знак бесконечности в пределе суммы понять, что нужно бесконечное число отсчётов. Конечно, всех деталей сразу не поймут, но это и не нужно — достаточно, чтобы детских заблуждений не появилось.
Про фильтры — да это не объяснение было, а так, намёк, где его искать. Для понимания лучше всего взять копию сигнала, сдвинуть на 1, 2, и т. д. сэмпла, сложить с оригиналом и посмотреть, что стало со спектром. А второй вариант — взять копию, инвертировать, прибавить и посмотреть, что стало со спектром. А можно взять три сигнала, и не просто сдвинуть и сложить, а ещё умножить часть, сдвинутую на 1 сэмпл, на 1/2, а сдвинутую на два — на -1/2.
Чтобы было легче смотреть, в качестве исходного сигнала возьмите белый шум — разница в спектре будет хорошо видна и слышна.
Сдвиг фаз? Вот он и появляется оттого, что мы сдвигаем сигнал на 1, 2,… сэмпла. Разный для разных частот потому, что сдвиг на 1 сэмпл (из 44100 Гц) на частотах 20 Гц и 20 КГц — это разный сдвиг по фазе.
В целом, вот то, что я тут описал, называется фильтр КИХ — с конечной импульсной характеристикой, он же FIR — finite impulse response. Считается просто, алгоритм реализуется в жёстком реальном времени, математически устойчив — всё хорошо, только вот копий сигнала приходится делать не три, а до нескольких тысяч. Правило простое: хотите, чтобы фильтр влиял на частоты порядка 20 Гц — вам нужно сдвигать сигнал на порядка 1/20 секунды, а при частоте дискретизации 44.1 это будет порядка 2K сэмплов. Может, потребуется в два раза больше, если хотите фильтр поточнее. Существует алгоритм построения FIR, реализующего заданную частотную характеристику с заданной точностью.gheljenor
13.11.2015 15:07+3Статей много, каждая о какой-то части данной статьи пишет гораздо более развёрнуто и зачастую гораздо более научным языком с кучей математики. А вот обзорной статьи, в которой бы на пальцах были объяснены основные принципы и обозначены темы для изучения я так и не нашёл. Самое близкое к этому — статья Тараса Ковриженко про нормализацию громкости.
Со знаком бесконечности как раз вопросов возникнет больше чем ответов — до этого речь идёт о каком-то конечном сигнале и тут вдруг возникает бесконечность. Откуда, почему? Если требуется бесконечное количество отсчётов, как в таком случае восстанавливать конечный сигнал? Вообще оцифровка сигнала и восстановление сигнала — это темы для двух больших отдельных статей, если не книг.
В данной конкретной реализации используется биквадратный фильтр. Он как я понял относится к фильтрам БИХ (с бесконечной импульсной характеристикой). Работает примерно также.
Берётся 2 последних отсчёта входного сигнала, 2 последних отсчёта выходного сигнала и текущий сигнал. Они умножаются на коэффициенты и складываются.
diakin
14.11.2015 19:02С тем же успехом можно сказать, что результат преобразования Фурье — «набор действительных чисел» )
merlin-vrn
14.11.2015 19:28ещё проще берите, набор цифр. Вы же не вычисляете его с бесконечной точностью, верно?
diakin
14.11.2015 19:39Я имею в виду, что результат можно представить или в комплексной или в действительной форме.
И сразу же станет видно, что результат преобразования — набор комплексных чисел
sci_nov
13.11.2015 17:07+3Подробнее про теорему Котельникова и дискретизацию сигналов
blog.amartynov.ru/archives/%D1%82%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0-%D0%BA%D0%BE%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA%D0%BE%D0%B2%D0%B0-%D0%B4%D0%B8%D1%81%D0%BA%D1%80%D0%B5%D1%82%D0%B8%D0%B7%D0%B0%D1%86%D0%B8%D1%8F
ZoomZoomZoom
16.11.2015 11:16+2Касательно измерения громкости:
На данный момент наиболее актуальным является стандарт измерения громкости ITU BS.1770-4 (предыдущая версия 2 используется в Европе как EBU R-128). Это полноценный стандарт, применяемый в аудио-, кино- и телеиндустрии.
Replaygain версии 1 измеряет воспринимаемую громкость, применяя фильтр обратный кривой Флетчера-Мансона и считающий RMS (вы эту аббревиатуру не упоминаете вообще и зря) 50мс отрезков аудио, плюс статистическая корректировка результата (описано упрощённо!).
Утверждение, что RG «наиболее точно передает воспринимаемый уровень громкости записи» неверно, чему является подтверждением тот факт, что в предлагаемой версии RG2 планируется использовать способ определения громкости из стандарта ITU BS.1770[1].
Часть про нормализацию полна неточностей. Нормализация — вполне конкретный термин, означающий увеличение амплитуды сигнала (т.е. повышение громкости) при которой пиковый уровень приводится к заданному значению, чаще всего к 0dBFS. Однако если говорить о нормализации громкости, то это уже комбинация алгоритмов её измерения с ограничением пиков (для предотвращения клиппинга).
Последний абзац настолько некорректен, что даже не знаю, что там комментировать.
[1] http://wiki.hydrogenaud.io/index.php?title=ReplayGain_2.0_specificationdtestyk
16.11.2015 11:39о нормализации громкости
А применяется ли фильтр, аналогичный эквилизации гистограммы для изображений?ZoomZoomZoom
16.11.2015 12:24Нет, так как нормализация аудио подразумевает недеструктивное изменение сигнала.
Мне вообще не очень легко представить адекватную аналогию такого преобразования. Возможно это могло бы быть расширение динамического диапазона, но толку в этом очень мало*.
*Можно говорить о расширении динамического диапазона (декомпрессии) как о восстановительном процессе для «убитого» звука, но это обычно контролируемый вручную процесс, применяемый чаще всего на этапе мастеринга записей.
pehat
geektimes.ru/post/247974/#comment_8432808