Поздравляю всех с (прошедшим) днем числа Пи! (день числа Пи отмечается 14 марта, поскольку эта дата в американском формате записывается в как 3.14 - прим. перев.) Чтобы отметить его как следует, я хочу ненадолго отвлечься от программного обеспечения и поговорить о чем-то особом. Возможно, вы слышали байку о том, как в штате Индиана пытались законодательно приравнять число Пи к чем-то типа 3, или 4, или 3.15. Обычно ее рассказывают в качестве доказательства того, что жители Индианы - бестолковая деревенщина, но это далеко не вся история. Зачем они пытались поменять значение π и на что они рассчитывали?
Предвосхищая комментарии: конечно, я знаю про константу τ и считаю ее более уместной для описания свойств круга. Однако никто не пытался поменять ее значение на законодательном уровне, не так ли?
Я занялся исследованием, и теперь могу рассказать историю целиком. Чтобы вы поняли контекст, мне придется объяснить кое-какие математические концепции.
Мне придется объяснить немало математических концепций.
Линейка и циркуль
Западная математическая традиция берет свое начало из Греции. Они были не первой цивилизацией, занимавшейся математикой, и многие приписываемые им вещи были открыты еще раньше математиками из Вавилона, Египта и Китая - однако эти исследования дошли до нас через античную Грецию. Также греки того времени имели неоспоримое превосходство в области геометрии, и особенно интересовались классом задач, называемым "Построение с помощью циркуля и линейки".
Если у вас есть бесконечно длинная неградуированная линейка и циркуль, какие формы вы можете построить и что можно получить из существующих форм? Сделать можно гораздо больше, чем вы думаете. Например, можно взять угол и получить его бисекцию, то есть провести линию, разделяющую его ровно пополам. Можно взять линию и построить из нее 32-угольник. Можно взять квадрат и построить другой квадрат, площадь которого будет ровно в 2 раза больше.
Некоторые задачи на построение греки так и не решили, однако это не значило, что задача нерешаема вообще. Некоторые слишком сложные для античности задачи были решены позже, например построение 17-угольника (решена в 1796 году). Одна из самых долго обсуждаемых задач такого рода называлась "квадратура круга": если у вас есть круг, можно ли построить квадрат точно такой же площади?
Теперь нужно очень точно сформулировать, что это значит. Если вы можете построить квадрат с погрешностью 0.00001% - это не считается. Если вы придумаете способ, решение которого будет стремиться к точному значению за бесконечное количество шагов - это не считается. Также не считается решение, требующее что-либо еще помимо немаркированной линейки и циркуля. Греки уже знали способ найти квадратуру круга с помощью градуированной линейки или архимедовой спирали - вопрос был именно в том, можно ли получить точную площадь с минимумом инструментов.
К эпохе Возрождения математики сходились во мнении, что это скорее всего невозможно, поскольку все мыслимые попытки провалились. В 1837 году ученый Пьер Ванцель подвел под это утверждение твердый фундамент. Площадь круга с радиусом 1 будет равна π, следовательно стороны квадрата должны иметь длину, равную √π. Ванцель доказал, что это значение можно получить только в том случае, если бы π было алгебраическим числом, а математики подозревали, что оно на самом деле трансцендентное.
Алгебраическое? Трансцендентное? Я позаимствую объяснение, написанное Марком Доминусом:
Сыграем в игру. Возьмите произвольное число X. Дальше вы можете использовать сложение, вычитание, деление и умножение на любое целое число. Вы также можете умножать результат на X. Операции можно производить сколько угодно раз. Если в результате вы получите 0 - вы победили.
Например, X = 2/3. Умножаем на 3, вычитаем 2, получаем 0 - вы победили!
Допустим, X равен ∛7. Умножаем на X, потом еще раз, потом вычитаем 7. Вы снова победили!
Теперь допустим, что X = √2 + √3. Тут увидеть решение уже не так просто. Но оказывается, что если умножить на X, вычесть 10, дважды умножить на X, а потом добавить 1, то вы тоже победите. Это абсолютно неочевидно, но вы можете попробовать выполнить это на калькуляторе.
А вот если X = π - вы не можете выиграть. Нет такого способа, позволившего бы получить 0 с помощью разрешенных действий, сколько бы раз вы их не повторяли. Это также очень хитрая, неочевидная штука.
Числа, с которыми вы можете победить, называются алгебраическими. Числа вроде π, с которыми вы не можете, называются трансцендентными.
Хотя "почти все" числа являются трансцендентными, доказать что конкретное число является таковым очень сложно. Мы даже не знаем, является ли таковым значение π + e. Тем не менее, в 1882 году Фердинанд фон Линдеманн доказал трансцендентность числа π - это значит, что построить сторону квадрата длиной √π невозможно, а следовательно и построить квадратуру круга тоже нельзя.
Быстрый набросок доказательства: действительные числа являются неисчислимыми. Каждое алгебраическое число является корнем некого полинома. Полиномы могут быть представлены в виде кортежа коэффициентов, например: x^2 - 3 → (1, 0, -3). Множество всех конечных списков является счетным, следовательно алгебраические числа также счетны. Если вычесть из несчетного множества действительных чисел счетное множество алгебраических, останутся трансцендентные.
Хочу еще раз подчеркнуть, что это практически не влияет на настоящие прикладные задачи. Получить приближенное решение легко, а если вам позарез необходимо получить точное значение - можно взять линейку с делениями.
Мракобесы
Даже после того, как математики доказали невозможность построения квадратуры круга, существует группа людей, продолжающих с энтузиазмом искать решения: мракобесы.
Мракобесы - это люди, глубоко и непоколебимо убежденные в чем-то внешне похожем на научные исследования, но на самом деле являющемся бредом сивой кобылы. Для завсегдатаев интернета самым известным примером наверняка является куб времени. Большинство мракобесов говорят более осмысленно, но руководствуются такой же инопланетной логикой. В любой области такие ребята есть: например, мракобесы от информатики опровергают проблему останова, доказывают равенство P и NP, и выдают вот такие охренительные шедевры (нет, серьезно, посмотрите - это божественно!).
Мракобесов в области математики также немало, и порядочное их число озабочены квадратурой круга и трисекцией угла. Я думаю, что причины следующие:
Задачу легко понять обывателю.
Задача известна за пределами математического сообщества. Мракобесов, решающих проблему Гольдбаха, гораздо меньше (но они тоже есть).
Задача выглядит так, будто ее можно "попытаться решить" без каких-либо познаний в математике: просто делай построения до тех пор, пока что-нибудь не получится.
Легко посчитать задачу решенной, если вы не понимаете нюансов насчет точного решения и использования только линейки и циркуля.
В книге "A Budget of Paradoxes" Огастес Де Морган упоминает более тридцати "квадратурщиков", с которыми он вел переписку. Читая его заметки из 1872 года, не перестаешь удивляться тому, как похожи тогдашние мракобесы на нынешних. Именно поэтому мракобесие настолько меня завораживает - в нем безумие противоречит конформизму. Какими бы ни были предметная область и эра, какие бы слова ни произносил мракобес - они всегда идут по тому же сценарию и говорят одно и то же. Именно поэтому мракобесие можно распознать, даже не вчитываясь - по соответствию форме все становится понятно. Это научная версия того, что в искусстве называют "ар-брют".
Эдвард Дж. Гудвин
Мракобесие возникает по-разному. В случае с Эдвардом Дж. Гудманом, к несчастью, причиной было психическое заболевание. Он считал, что доказательства ниспосланы ему свыше - в прямом смысле слова Бога. В 1888 году Бог рассказал ему, как построить квадратуру круга. Полное описание метода можно прочитать здесь, но вот его краткое содержание: сначала берем 90-градусную дугу и проводим хорду между ее концами. Отношение длины дуги к хорде будет равно 8:7, а длины хорды к основанию треугольника - 10:7. Из произведения этих величин следует, что длина основания равна 4/5 длины дуги, а поскольку мы рассматривали только четверть круга, то умножение на 4 даст нам искомое значение: 16/5. Далее построение является тривиальным.
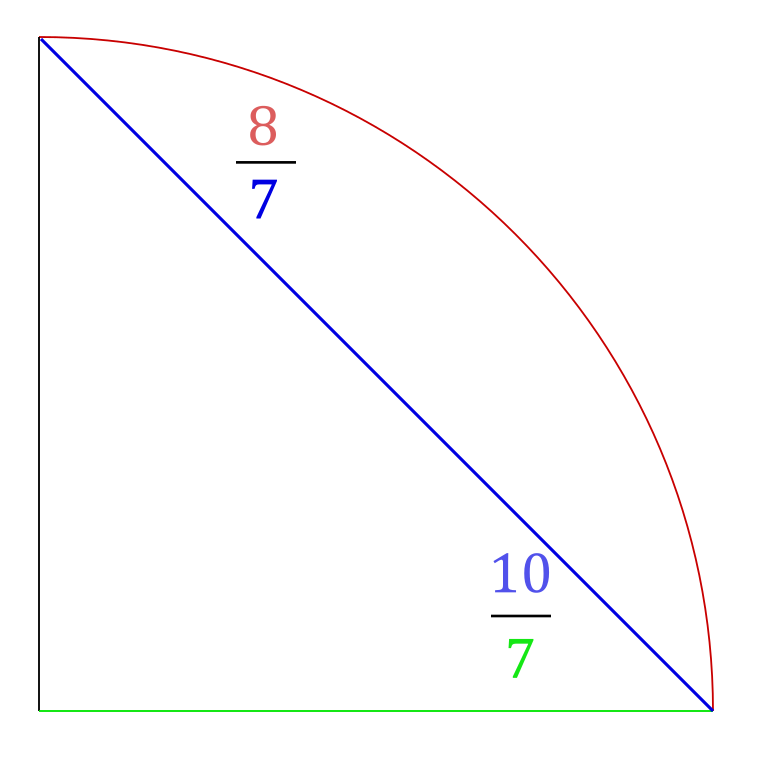
Уследили за ходом мысли? Надеюсь, что нет! Я потратил три часа, разглядывая это доказательство и пытаясь понять, что, черт возьми, творилось у него в голове. Должен сказать, что заставить себя думать как мракобес отнюдь не просто. Теперь эта инопланетная логика отпечаталась у меня в голове. Я на один шаг приблизился к тому, чтобы самому стать мракобесом. Чего я только не делаю ради вас!
Самое важное для нашей истории - это соотношения, которые он использовал: 8:7 и 10:7. Они примерно на 2% и 1% отличаются от настоящих значений π/2 и √2 соответственно, и из них мы можем получить значение π c погрешностью примерно 4% (160/49). Гудвин дальше совершил еще две ошибки, которые по стечению обстоятельств отменили друг друга, и пришел к чуть более точному значению π = 3.2.
Во-первых, он умножил на 7/10, а не на 10/7.
Во-вторых, он умножил на 4 (окружность состоит из 4 таких дуг), но не поделил на 2 (диаметр равен удвоенному радиусу).
Сразу оговорюсь: это не единственная его ошибка вообще, а единственная очевидная ошибка в вычислениях. Непонятно, как именно переопределение π позволяет ему построить квадратуру круга. Если предположить, что это сработает, стороны получаемого квадрата будут примерно на 1% длиннее - погрешность достаточно малая, чтобы на глазок решение казалось верным.
Гудвин отмечает расхождение между его значением 3.2 и "общепризнанным" 3.1416, а потом заявляет, что 3.1416 - ошибочное. Это, на мой взгляд, самое захватывающее и жуткое в мракобесии. Даже если это что-то несусветное и легко опровергается эмпирически, их вера в собственное утверждение непоколебима. Слабые метакогнитивные способности не позволяют им даже допустить собственную неправоту. Это не он где-то сделал ошибку, а все остальные облажались. Многим мракобесам присущи иллюзии величия, они сравнивают себя с Галиллеем или Эйнштейном. Впрочем, если бы я думал, что обладаю истинным знанием о вселенной, я бы тоже сравнивал.
Идем в правительство!
Итак, у Гудвина появился способ в прямом смысле сделать невозможное. Как о нем рассказать? Конечно, его нужно опубликовать! В 1894 году он отправил свое доказательство в Американский Ежемесячный Математический Журнал (American Mathematical Monthly, AMM), который опубликовал его в июльском выпуске.
Как оно могло туда попасть? Просто повезло. AMM был основан всего за 7 месяцев до этого, и редакторы еще не определились с курсом издания. Общее направление заключалось в том, чтобы сделать математику доступнее и интереснее для широкой аудитории, и они пробовали различные способы этого добиться. Как писал один историк, в первое время они печатали "все, что присылали - или по крайней мере то, на что хватало места". Сначала они печатали "высшую пробу", а потом уже все остальное. Доказательство Гудвина было опубликовано в разделе "Запросы и информация", который редакторы не проверяли вообще.
Также в этом разделе постоянно творилась перепалка между авторами.
Но тонкости внутренней работы издательства для большинства недоступны: они думают, что "опубликовано" и "признано" - одно и то же. Это дало Гудвину желаемую убедительность и раздуло его мракобесские амбиции. В 1889 году он уже оформил "копирайт" на свое доказательство, и теперь, думая, что все математическое сообщество его поддерживает, решил заработать на нем денег. Он считал, что открытие такого масштаба должны проходить в каждой школе, а значит каждая школа должна платить ему отчисления за использование его доказательства. Поэтому в 1897 году он обратился в законодательные органы штата Индиана с предложением: они официально объявят его доказательство верным, а он взамен позволит им использовать его бесплатно, что сэкономит государству кучу денег.
Так что да, мотивация правительства штата Индиана была в экономии бюджетных средств.
Закон можно прочитать целиком по этой ссылке.
Новое платье короля
Не до конца понятно, как именно постановление прошло рассмотрение. Некоторые люди спекулируют, что члены палаты представителей не обладали математической грамотностью и не поняли, что фраза "диаметр относится к длине окружности, как пять четвертых к пяти" была про число π. Мне же кажется, что поначалу они догадывались, что это брехня! Вот что пишет The Telegraph:
Гаст из Блумингтона, демократ, под громкий хохот заявил, что постановление нужно отправить в Министерство Финансов, поскольку оно взяло на себя ответственность за решение глобальных задач и обладает свободным временем. Другой представитель поднялся и высказал мнение, что более уместным окажется Министерство Болот. В такой шутливой обстановке спикер отправил "Квадратуру Круга" в Министерство Болот, где, в болоте, постановление и найдет достойную могилу.
Но потом Министерство Каналов ("болот") отправило его в Министерство Образования, а оттуда оно вернулось с полной поддержкой государственного управляющего. Постановление было принято с 67 голосами "за" и без единого голоса "против". Как же так? Моя догадка: никто, по иронии, не хотел показаться глупым. Большинство людей не знакомы с мракобесием и не могут с легкостью отличить бред от фактов, которые просто звучат неправдоподобно для не разбирающегося в теме человека. Вы действительно хотите быть тем человеком, который вздумал попрепираться с Эйнштейном? По крайней мере, этого хватило, чтобы убедить газету Indianapolis Journal:
Среднестатистический редактор не добьется ничего особого, поднимая на смех открытие, признанное Американским Математическим Журналом, подтвержденное профессорами Национальной Астрономической Обсерватории Вашингтона (в том числе профессором Холлом, который открыл спутники Марса), объявленное "безупречным" профессорами из университетов Энн Арбор и Джона Хопкинса, а также запатентованное в семи странах Европы. Он едва ли настолько подкован в математике, чтобы противостоять их совместному авторитету.
Может быть, это и палату представителей тоже убедило? На мой взгляд, звучит вполне правдоподобно, но это спекуляция.
Гудвин утверждал, что обсудил это с Аcафом Холлом, и все поверили ему на слово. Почему именно с ним? Возможно потому, что он первым публично провел эксперимент Бюффона с бросанием иглы - это способ вычисления π с помощью случайной выборки. Могу представить, как Гудман услышал про это и решил, что Холл тоже пытается найти его истинное значение - еще один ске(π)тик.
Какими бы ни были причины, постановление прошло, и Сенат тоже собирался его принять. Но так случилось, что на той неделе в Капитолии оказался математик из университета Purdue. Кто-то из сенаторов спросил его мнение, и ученый объяснил, почему доказательство было чушью - в результате постановление ушло в стол. Думаю, что это подтверждает мою гипотезу: мракобес может сойти за эксперта и заставить людей усомниться в себе, но когда в дело вступает настоящий эксперт, заклинание рассеивается.
Гудвин умер спустя 5 лет в возрасте 77. Многие его знакомые все еще в него верили. Из его некролога:
Годы шли, а дитя его гения оставалось непринятым математическим сообществом. Он был разбит досадой, но никогда не терял надежды на то, что доживет до момента, когда мир узрит величие его замысла, а он испытает мимолетное блаженство успеха. На фоне размеренной деревенской жизни разыгралась трагедия нереализованных амбиций.
В чем мораль этой истории? Большинство людей ограничиваются выводом о том, что американцы / жители Индианы / политики - тупицы. Я же считаю, что главное в истории - мракобесие. Оно нарушает наши эпистемологические нормы, подавая абсолютную неправоту с абсолютной самоуверенностью. Мало кто оказывается к этому готов. Гудвин, по всем меркам, обладал харизмой и говорил убедительно. Он вел себя как человек, которому можно верить - люди и верили, и от его лица чуть не развалили геометрию.
Но если не брать в расчет его почти-успех, Гудвин ничем не отличался от других мракобесов. Он думал, писал и действовал точно так же. Я иногда получаю электронную почту с таким же мракобесным настроением. Сто лет прошло, а оно ни капли не поменялось.
Комментарии (137)

SerjV
15.04.2023 12:55+4если число Пи представляет собой бесконечную дробь, значит площадь круга тоже бесконечное число?
"Бесконечная дробь" не то же самое, что "бесконечное число". А так да, площадь круга будет обладать бесконечной дробной частью.
Ну кроме случая, если радиус круга представим в виде дроби, в знаменателе которой квадратный корень из пи, а все остальные составляющие дроби - рациональные числа :)

ruomserg
15.04.2023 12:55+10Мне не нравится формулировка "бесконечное число". Слишком много простора для интерпретаций. Очевидно, что площадь круга (как величина) будет конечной. Однако, записать ее конечным число десятичных знаков — не получится. С третьей стороны, никто не мешает вам завести систему счисления (или хотя бы систему линейных единиц) с основанием кратным Пи, и в ней площадь круга будет выражаться конечной десятичной дробью. Неудобством такой системы будет тот факт, что в ней бесконечной дробью придется записывать привычные натуральные числа (одна корова = 0.3184..., две коровы = 0.6369..., и т.д.). А поскольку натуральные числа нам милее и пользуемся мы ими чаще, то приходится мириться с бесконечным числом цифр в точной записи площади круга.

SerjV
15.04.2023 12:55+1Мне не нравится формулировка "бесконечное число". Слишком много простора для интерпретаций. Очевидно, что площадь круга (как величина) будет конечной.
"Бесконечная дробь" действительно есть такой термин, существующий потому, что слишком долго говорить "бесконечное число знаков в дробной части числа, записанного в десятичной системе счисления". Можно сказать проще - "имеет бесконечное число знаков после запятой", но тут есть другой нюанс - в некоторых странах дробную часть числа принято отделять точкой (а запятая в этом случае - разделитель разрядов).
Ну и если на то пошло, то в моём сообщении было бы правильнее сказать "если радиус представим в виде дроби вида a / (b * sqrt(pi)), где a - целое неотрицательное число, b - натуральное число"- тогда мы получим площадь круга, представимую рациональным числом (причём неотрицательным, но это уже детали).
И да, там рядом подчеркнули важный момент, почему уточнение про рациональные числа важны - а не это клиенто-ориентированное "мы тут на самом деле догадались, что клиент имел в виду": рациональные числа тоже могут представляться в виде бесконечной десятичной дроби, но в отличии от иррациональных чисел - это будет бесконечная периодическая дробь (и/или дробь будет конечной).
А вот с "бесконечными числами" есть нюанс, ага... Только это не число знаков после запятой, а всякие +∞, −∞ и бесконечно малые числа. И площадь круга конечного радиуса - ну никак не может быть бесконечным числом.
Вот такая вот притча о важности точных формулировок получилась...

PereslavlFoto
15.04.2023 12:55Итак, пи не бесконечное число. На каком знаке после запятой заканчивается число пи?
Спасибо.

SerjV
15.04.2023 12:55+3Пи конечно не бесконечное число, но для ответа на ваш вопрос надо сперва дать определение конечного и бесконечного числа, прежде чем ожидать ответа на него.
Вот в теории множеств там да, есть конечные, бесконечные, счётные, эквивалентные множества.
А то, знаете ли, можем еще и до трансфинитных чисел тут договориться...
Пожалуйста.

Feedman
15.04.2023 12:55-1Дробные числа это же тоже числа?

ruomserg
15.04.2023 12:55"Число" — это абстракция (см аксиоматическое определение чисел, или определение чисел как частного случая множеств). Дальше надо понимать, что есть "дробные числа"? Вижу два варианта — либо подмножество рациональных чисел, не являющихся целыми, либо подмножество чисел которые можно записать конечными десятичными дробями. Эти два варианта не эквиваленты друг другу, но тем не менее при любом из этих определений — "дробные числа" являются подмножеством "чисел вообще".

Feedman
15.04.2023 12:55Значит можно сказать, что бесконечная дробь это и есть бесконечное число? Впрочем это несущественно. Меня интересует другое - получается вычислить точную площадь круга/длину окружности невозможно?

victor_1212
15.04.2023 12:55конечно, просто написать точный результат например для случая R=1 не хватит всех элементарных частиц вселенной, если предположим на каждой можно было бы разместить по одной цифре, тоже самое верно для диагонали квадрата со стороной 1, элементарное доказательство того что диагональ такого квадрата не является рациональным числом и поэтому например не может быть представлена как десятичная дробь конечной длины было известно грекам практически одновременно с получением доказательства теоремы Пифагора, и в общем произвело шокирующий эффект,
что можно понять, поскольку принято было считать, что длины отрезков и числа в принципе эквивалентные понятия, а длину в принципе всегда можно точно измерить, если иметь линейку с достаточно мелкой разметкой, а тут получается диагональ это такой отрезок, длину которого невозможно точно измерить, последствия для человека сделавшего это открытие были печальными, типа объявили разрушителем науки, святотатцем и приговорили к смерти,
но уже следующее поколение поняло, что дело в необходимости абстракции, что привело сразу к нескольким интересным вещам, во-первых приоритетному развитию геометрии, как более наглядной и понятной области математики, тогда как все что опиралось на понятие числа казалось связанным с неразрешимыми парадоксами, развитие алгебры практически остановилось на >1000 лет, и во-вторых развитию понятия аксиомы как логического основания для работы с абстракциями типа прямой линии, плоскости и т.д.

ruomserg
15.04.2023 12:55+3Вычислить — никаких проблем не будет. Формула дает абсолютно точное значение, указывающее на совершенно конкретную точку числовой прямой (а не на отрезок, как это было бы в случае с приблизительным вычислением с погрешностью). Проблемы у нас возникают только в том случае, если мы пытаемся записать полученное значение площади/длины окружности конечным числом цифр в принятой у нас системе счисления. Как говорится: "… жопа есть, а слова — нет!" :-) В этом смысле, ввод в оборот символьного значения \phi позволяет избежать потери точности при записи промежуточных результатов (а там, кто знает — может быть эта иррациональность где-нибудь в вычислениях сама-собой сократится — например, если нас интересует не площадь, а отношение площадей).

victor_1212
15.04.2023 12:55> Вычислить — никаких проблем не будет. Формула дает абсолютно точное значение
формула это последовательность знаков и символов, сама по себе ничего не дает, позволяет вычислить только приближенно, например потому что для вычисления абсолютно точного значения потребуется бесконечно много времени, совершенно конкретная точка числовой прямой существует только в нашем воображении, реально прямых линий нулевой толщины и бесконечной длины в природе не наблюдается

SerjV
15.04.2023 12:55+3формула это последовательность знаков и символов, сама по себе ничего не дает, позволяет вычислить только приближенно, например потому что для вычисления абсолютно точного значения потребуется бесконечно много времени
Неверно.
Формула даёт абсолютно точное значение. Но надо различать аналитическую и числовую форму значения. Точность гарантируется только в аналитическом виде, в числовом - зависит от выбранной формы представления чисел.

victor_1212
15.04.2023 12:55> Точность гарантируется только в аналитическом виде, в числовом - зависит от выбранной формы представления чисел.
не стоит смешивать точность аналитическую и числовую, иначе возможна подмена понятий, то что "точность в числовом виде зависит от выбранной формы представления" не вызывает сомнений, другое дело что это далеко не все, и в практических применениях просто верхушка айсберга, состоящего в том числе из алгоритма и его реализации,
аналитическое значение это обычно новая формула, возможно более простая, но "совершенно конкретная точка на числовой прямой" является абстракцией, поэтому то что здесь названо вычислением точного значения с равным успехом можно назвать воображаемым вычислением на воображаемой прямой (в мире эйдосов по платону),
согласен что терминология собственно математики вне своей рабочей области может пониматься неоднозначно, в свое время закончил мехмат, и вероятно не хуже Вас знаю что такое аналитическая форма, но в данном контексте (вычисление pi) эта терминология представляется неудачной,
скажем что именно дает формула Ramanujan'a - ряд с довольно приличной сходимостью не более, или один из способов вычислить достаточно много десятичных знаков, ни о какой абсолютной точности (в разумном смысле) для значения pi говорить нельзя

SerjV
15.04.2023 12:55не стоит смешивать точность аналитическую и числовую, иначе возможна подмена понятий, то что "точность в числовом виде зависит от выбранной формы представления"
Вот не надо смешивать аналитическое и численное решения, для начала. У аналитического решения ответ абсолютно точный всегда (решение может быть не всегда, но это уже совсем другая история). У численных методов - точность решения не гарантируется.
А вот от формы представления чисел действительно может многое зависеть. Т.к. возможны ситуации, когда одно и то же число может быть представлено абсолютно точно, но вот на пересчёт его значения в другую систему счисления может потребоваться то самое ваше бесконечное время.

SerjV
15.04.2023 12:55аналитическое значение это обычно новая формула, возможно более простая, но "совершенно конкретная точка на числовой прямой" является абстракцией
Ну и строго говоря, в математике всё - абстракции.
Потому говорить о "практических применениях" надо очень, очень осторожно. Потому что можно незаметно для всех выйти за рамки математики, ну или применить не те разделы математики, которые оптимальны для применения для конкретной практической задачи.

victor_1212
15.04.2023 12:55> Потому что можно незаметно для всех выйти за рамки математики
это интересно, более конкретно если можно, также пару слов про Ваш background, просто для лучшего понимания (типа если с мехмата какая кафедра)
ps
как по Вашему - асимптотики имеют отношение к аналитическим решениям?

victor_1212
15.04.2023 12:55pps
вопрос о background не актуален, достаточно высказываний в комментариях на разные технические темы, при всем уважении Вы не математик, а жаль :)

SerjV
15.04.2023 12:55+1это интересно, более конкретно если можно
А уж куда конкретнее. Математика - это наука, изучающая сама себя. Но в тоже время являющаяся инструментом для многих других наук, той же физики, которые изучают нечто реальное.
Поэтому когда вы говорите о "практических применениях", то можно очень легко начать говорить не о математической стороне вопроса, а, например, "сколько единиц длины отмерять от того столба", где вопрос точности стоит совсем по-другому, а абсолютная точность вообще не нужна.

victor_1212
15.04.2023 12:55> А уж куда конкретнее. Математика - это наука, изучающая сама себя.
конкретнее означает без общих слов, и по возможности с примерами, для умного человека каким Вы несомненно являетесь должно быть понятно, не то чтобы Ваш ответ не устраивал, меня все устраивает просто рассуждения тривиальны, про то что именно изучает математика вопрос супер интересный, но не на таком уровне

victor_1212
15.04.2023 12:55ps
если интересуетесь, посмотрите известную дискуссию Wittgenstein-Turing (желательно в оригинале без комментариев типа wiki) и напишите что думаете

Spaceoddity
15.04.2023 12:55Числа бывают:
рациональные - могут быть выражены в виде простой дроби - 1/3 или десятичной с конечным периодом - 0.3(3)
иррациональные - не могут быть представлены в виде простой или периодичной дроби - различные корни из простых чисел, пи, основание натуральных логарифмов и т.п. выражаются какой-либо "бесконечной записью" (ряд, десятичная дробь без повторяющегося периода и т.п.)
трансцендентные - частный случай иррациональных. так же не могут быть выражены конечной записью и при этом не могут являться корнями какого-либо уравнения. т.е. π и e - трансцендентные числа (не являются корнями алгебраического уравнения), а вот √2 - иррациональное, но не трансцендентное, поскольку является корнем уравнения x² = 2
Вычислить точную площадь круга можно. Зависит от того, чему равен радиус. Отношение радиуса окружности и её длины выражается через π. Т.е. с абсолютной точностью можно представить или радиус окружности, или площадь круга (если радиус можно выразить через √π); но не обе величины одновременно, поскольку они находятся в зависимости, не выражаемой через алгебраическое представления.
Вот и всё что вам надо знать на эту тему))

SerjV
15.04.2023 12:55трансцендентные - частный случай иррациональных
Не совсем так - трансцендентное число может быть не только вещественным. Но любое трансцендентное вещественное число является иррациональным, это верно.
Потому что помимо известной иерархии "натуральные - целые - рациональные/иррациональные - действительные" числа есть и другие (комплексные, двойные, дуальные, внедуальные, много их...), в некоторых видах чисел можно делить на ноль, например.

Spaceoddity
15.04.2023 12:55я это знаю. я даже ждал подобного комментария)) ну как в математической дискуссии не доколебаться до терминологии?)) у меня уже второй раз в этом треде, между прочим))
я дал определения (причём максимально упрощенные - поскольку изначальный вопрос звучал довольно "по-нубски") только тем типам чисел, которые важны для понимания текущей темы. всё. вы ещё спросите почему я трансфинитные не упомянул))

SerjV
15.04.2023 12:55В "самом исходном вопросе" исходят из того, что "бесконечная дробь" и "бесконечное число" - одно и то же ;) Так что как раз с терминологии тут и надо начинать, а то получится как в разговоре двух глухих "ты в баню? нет, я в баню! а-а, а я думал, что ты в баню!"

Feedman
15.04.2023 12:55ничего не понял
Вот возьмем площадь прямоугольника. Вычислить точную площадь можно вне зависимости от длины сторон. Так?
А для круга точность вычисления зависит от длины радиуса что ли? Для X точную площадь вычислить можно, а для Y уже нельзя?

Spaceoddity
15.04.2023 12:55+1Вот возьмем площадь прямоугольника. Вычислить точную площадь можно вне зависимости от длины сторон. Так?
Нет. Если у вас одна из сторон равняется тому же π, а другая, скажем = e - абсолютно точно площадь вы не посчитаете (избавившись от математических констант в ответе).
Проблема с кругом в том, что одна из этих математических констант (с бесконечной записью в общепринятых системах счисления) изначально заложена в формулу вычисления площади круга.
Т.е. "неточности" в площади прямоугольника - это частный случай (когда используются трансцендентные числа в качестве длины сторон). А "неточность" в площади круга заложена изначально - избавиться от неё можно только если радиус круга пропорционален 1/√π - и вот для круга уже это является частным случаем.
Ну что тут непонятного?
π - отношение длины окружности к её диаметру. Это отношение представлено трансцендентным числом и в принципе не может быть выражено с абсолютной точностью.
Если интересно, то один из самых простых способов вычисления π - это ряд Лейбница:
π/4 = 1 - 1/3 + 1/5 - 1/7 + 1/9...
Feedman
15.04.2023 12:55Нет. Если у вас одна из сторон равняется тому же π, а другая, скажем = e - абсолютно точно площадь вы не посчитаете (избавившись от математических констант в ответе).
Еще раз - вне зависимости от длины стороны п-ка, его стороны представляют собой отрезки, т.е. имеют начало и конец. Соответственно вычисленная площадь будет иметь конечное значение. Либо, если признать, что пи и е имеют бесконечно кол-во знаков после запятой, то построить замкнутую фигуру с такой длиной стороны невозможно.
Проблема с кругом в другом. Кстати, тут вроде кто-то писал, что площадь круга невозможно выразить в десятичном формате. Это очевидно неверное утверждение - площадь круга конечна, соответственно нет никаких препятствий тому, чтобы выразить эту площадь в десятичном формате. Но очевидно не существует способа вычислить абсолютную площадь круга?

SerjV
15.04.2023 12:55Еще раз - вне зависимости от длины стороны п-ка, его стороны представляют собой отрезки, т.е. имеют начало и конец. Соответственно вычисленная площадь будет иметь конечное значение.
Площадь будет конечной величиной, даже если она будет выражаться иррациональным числом. Да-да, иррациональную площадь прямоугольника тоже никто не запрещал.
И такой прямоугольник можно получить элементарными геометрическими построениями.
Это вам не кубический корень вычислять с помощью циркуля и линейки.
Либо, если признать, что пи и е имеют бесконечно кол-во знаков после запятой, то построить замкнутую фигуру с такой длиной стороны невозможно.
Длина отрезка может быть любым действительным числом. В т.ч. e и пи.
Проблема с кругом в другом. Кстати, тут вроде кто-то писал, что площадь круга невозможно выразить в десятичном формате. Это очевидно неверное утверждение
Проблема с кругом в том, что вы старательно подводите под подмену понятий - конечность величины прощади фигуры противопоставляете бесконечному числу знаков после запятой в её десятичном представлении.

vesper-bot
15.04.2023 12:55+1Ну корень из двух тоже имеет бесконечное количество знаков после запятой, однако имея отрезок длиной 1, построить отрезок длиной в корень из двух во-первых довольно просто, во-вторых площадь квадрата с такой стороной будет очень простым числом. При этом площадь прямоугольника со сторонами 1 и корень из двух также будет числом с бесконечным количеством знаков после запятой. Так что вы неправы, бесконечность записи числа (не забываем, что 1/3 та же бесконечной длины) совсем не означает невозможность построения отрезка такой длины, и всему остальному, следующему из неё.

SerjV
15.04.2023 12:55Ну корень из двух тоже имеет бесконечное количество знаков после запятой, однако имея отрезок длиной 1, построить отрезок длиной в корень из двух во-первых довольно просто, во-вторых площадь квадрата с такой стороной будет очень простым числом. При этом площадь прямоугольника со сторонами 1 и корень из двух также будет числом с бесконечным количеством знаков после запятой.
Именно! :)
И при этом мы не вышли за рамки "циркуля и линейки".
не забываем, что 1/3 та же бесконечной длины
А поделить отрезок на 3 части вполне можно. Так что да, это еще один пример.

Spaceoddity
15.04.2023 12:55А поделить отрезок на 3 части вполне можно. Так что да, это еще один пример.
Ну на одной старейшей задаче о квадратуре круга мы уже попиарились. Вы теперь к другой решили подвести?))

SerjV
15.04.2023 12:55Ну на одной старейшей задаче о квадратуре круга мы уже попиарились. Вы теперь к другой решили подвести?))
Эм... Я ж не угол делить собрался :) Про него тут и без меня красочно рассказали, вместе с ящиком коньяка.
Хотя, можно предложить кубический корень найти с помощью циркуля и линейки, вдруг смогут.
Или вы о чём?

Spaceoddity
15.04.2023 12:55О трисекции угла, о ней родимой))
Оппонента просто надо было сразу отправить в "Занимательную геометрию" Перельмана. Там как раз целый раздел об этом всём. О достаточной точности числа Пи очень доходчиво рассказывается...


SerjV
15.04.2023 12:55О трисекции угла, о ней родимой))
После того, как о ней ниже красочно Zangasta рассказал детективную историю со спором на ящик коньяка... Я даже не подумал, что кто-то тут еще может на это повестись ;)
Но Перельман да, он наше всё ;)
p.s. а еще можно получить квадрат с иррациональной площадью, причём даже без трансцендентных чисел. Ну чтоб совсем было весело оппоненту.

SerjV
15.04.2023 12:55Т.е. "неточности" в площади прямоугольника - это частный случай (когда используются трансцендентные числа в качестве длины сторон)
Можно и без трансцендентных чисел получить иррациональное значение площади, никто не мешает.
е-пи был применён просто для опровержения утверждения с квантором всеобщности.

Spaceoddity
15.04.2023 12:55Опять вы мне зачем-то отвечаете... Комфортно так воевать на два фронта?))
Без трансцендентных чисел от иррациональности можно избавиться (иногда) путем алгебраических или геометрических преобразований.
Если вы возьмёте для примера иррациональные числа - ваш оппонент может сообразить, что если взять квадрат со стороной √2, то его площадь будет выражена вполне себе рациональным (и даже натуральным) числом. И потом вам всё сложнее будет вести дальнейшую дискуссию, поскольку "иррациональные числа никак не мешают точному вычислению площади"... Я смотрю, вы уже упёрлись в "пуленепробиваемый аргумент" о "конечности, но безграничности"))

SerjV
15.04.2023 12:55Опять вы мне зачем-то отвечаете...
С вами интереснее, вы понимаете, о чём речь :) Так что хоть поговорить можно, а не воевать.
Если вы возьмёте для примера иррациональные числа
Ну так тут и по этому поводу примеров накидали тут уже - как геометрически получить сторону прямоугольника, выражаемую иррациональным числом, или натуральной дробью, бесконечной в десятичной выражении.
Я смотрю, вы уже упёрлись в "пуленепробиваемый аргумент"
Да не, там проще - он утверждал, что для любых значений сторон прямоугольника площадь находится без бесконечных дробей. Мне в этом было "достаточно" квантора всеобщности. Вот если бы он утверждал о существовании, то да, другое дело.

SerjV
15.04.2023 12:55Вижу два варианта — либо подмножество рациональных чисел, не являющихся целыми, либо подмножество чисел которые можно записать конечными десятичными дробями.
Рациональные числа - это числа, представимые в виде обыкновенной дроби m/n, где m - целое, n - натуральное, числа.
Система счисления значения не имеет. Конечность или бесконечность, но периодичность, дробной части в десятичной системе счисления - это свойство, но не определение.
Т.е. любое рациональное число представимо в виде дробной записи, даже если оно целое или натуральное.
А дробные числа - это числа, дробная запись которых не сокращается до целого числа.

SerjV
15.04.2023 12:55Дробные числа это же тоже числа?
Числа, но есть нюанс - говоря о бесконечной дроби, имеют в виду бесконечность дробной части действительного числа в позиционной системе счисления. Ну или "более привычно по-русски" - бесконечное число знаков после запятой.

Feedman
15.04.2023 12:55Значит дробное число это все-таки число. под "бесконечным" в данном случае, я подразумеваю именно количество знаков после запятой. То есть используя десятичную систему, мы не можем получить абсолютно точное значение площади круга?

SerjV
15.04.2023 12:55В десятичном представлении - нет, кроме случая, "если радиус представим в виде дроби вида a / (b * sqrt(pi)), где a - целое неотрицательное число, b - натуральное число"- тогда мы получим площадь круга, представимую неотрицательным рациональным числом

Feedman
15.04.2023 12:55Но представить площадь круга в десятичном виде возможно - окружность является замкнутой фигурой, и соответственно ее площадь конечна. Но методики расчета не существует?

SerjV
15.04.2023 12:55А вы не путайте конечность величины и конечность числа знаков после запятой в её значении, не путайте :)
Значение площади определяется абсолютно точно. За конечное время в десятичном представлении её значение можно получить с любой конечной точностью. Либо не в десятичном представлении.

Feedman
15.04.2023 12:55А вы не путайте конечность величины и конечность числа знаков после запятой в её значении, не путайте :)
в чем разница в данном случае?
Значение площади определяется абсолютно точно
Как? если взять прямоугольник, то его площадь по формуле определятся абсолютно точно для любых значений сторон.
Для круга насколько понимаю такое невозможно

SerjV
15.04.2023 12:55Как? если взять прямоугольник, то его площадь по формуле определятся абсолютно точно для любых значений сторон.
Ложь. Возьмём квадрат со стороной длиной e, или pi... В десятичном представлении точного значения площади вы не получите.
p.s. Или еще лучше, возьмём прямоугольник со сторонами длиной e и pi, ищите абсолютно точное значение этого "е-пи".

Feedman
15.04.2023 12:55-1Квадрат с длиной e или p это абстрактное понятие. Но в реальном мире таких нет.. Только не надо словесной эквилибристики про реальный, нереальный мир. Упрощу задачу - чему равно площадь квадрата с длиной стороны 1 м: И чему равно площадь круга с радиусом 1 м?

Rsa97
15.04.2023 12:55+1Так и квадрат со стороной 1м это абстрактное понятие. Покажите мне такой квадрат в реальности. Только чтобы всё было выдержано с абсолютной точностью — длины сторон, их прямизна, углы. Обязательно окажется, что где-то что-то неровно.

Rsa97
15.04.2023 12:55Ровно такие же придирки, как и "Квадрат с длиной e или p это абстрактное понятие. Но в реальном мире таких нет.."

SerjV
15.04.2023 12:55Ровно такие же придирки, как и "Квадрат с длиной e или p это абстрактное понятие. Но в реальном мире таких нет.."
Вот пусть "кому надо" и доказывает, что в реальном мире нет квадратов (частный случай прямоугольников) со стороной e или pi, ну или прямоугольников со стороной e и pi.
Если сможет доказать, конечно. "Очевидно" и прочие доказательства уровня "мамой клянусь" не принимаются, разумеется.
Зачем делать чужую работу? ;)))
p.s. а так-то да, в реальном мире всё существует с некоторой погрешностью измерения, ибо идеальных измерительных приборов не существует. Но это уже выводит нас за рамки математики.
p.p.s. Мой пример не единственный возможный, просто его достаточно для опровержения утверждения (а так можно было бы и без трансцендентных чисел обойтись, например, но это упражнение я оставлю для задавшего вопрос, ну или для желающих - например, можно подобрать пример, имеющий геометрическую интерпретацию). А то ведь можно начать бесконечно уточнять "что имел в виду заказчик" и придумывать убедительные для него объяснения. Но это тоже выводит нас за рамки математики.

SerjV
15.04.2023 12:55Квадрат с длиной e или p это абстрактное понятие. Но в реальном мире таких нет.. Только не надо словесной эквилибристики про реальный, нереальный мир.
Философия тут не нужна. Вы сказали "если взять прямоугольник, то его площадь по формуле определятся абсолютно точно для ЛЮБЫХ значений сторон".
Для опровержения достаточно любого одного примера. Пример приведён. Ч.т.д.

Feedman
15.04.2023 12:55-1Пример так себе, ибо прямоугольник с длиной стороны е или пи существовать не может, ибо состоит из отрезков, ограниченных перпендикулярами. Но ваша точка зрения мне тоже понятна.

SerjV
15.04.2023 12:55Пример так себе, ибо прямоугольник с длиной стороны е или пи существовать не может, ибо состоит из отрезков, ограниченных перпендикулярами.
В математике что-то мешает существовать отрезку длиной e, или там pi? Доказывайте! :)

Feedman
15.04.2023 12:55А разве само определение понятия "отрезок" не мешает существованию такового с иррациональной длиной?

Rsa97
15.04.2023 12:55Не мешает. В евклидовом пространстве отрезок прямой — часть прямой, ограниченная двумя точками. Расстояние между концами отрезка называют его длиной. Взяв, например, на оси абцисс точки 0 и pi получим отрезок длиной pi. Взяв на оси ординат точки 0 и e получим отрезок длиной e. Скопировав первый отрезок на e вверх, а второй на pi вправо получим четыре отрезка, образующих прямоугольник со сторонами pi и e.

Feedman
15.04.2023 12:55У отрезка в любом случае будут начальная и конечная точка. соответственно можно будет вычислить площадь (абсолютную или как ее назвать?)

SerjV
15.04.2023 12:55У отрезка в любом случае будут начальная и конечная точка. соответственно можно будет вычислить площадь
Если не наложить запрет на вырожденные прямоугольники, то площадь действительно будет. Нулевая.
Или вы о площади чего говорите?

SerjV
15.04.2023 12:55А разве само определение понятия "отрезок" не мешает существованию такового с иррациональной длиной?
Не мешает. Более того, отрезок длиной, измеряемой иррациональным числом, можно получить чисто геометрически.

Feedman
15.04.2023 12:55Да, кстати, вот отрезок более простой пример. Значит существуют отрезки, абсолютную длину которых можно рассчитать/измерить, и такие, для которых это сделать нельзя?
Например гипотенуза треугольника с катетами 3 и 4 будет 5. Можно ее измерять с любой точностью, считать, но она всегда будет 5.
Для треугольника со катетами 1 такой расчет/измерение можно сделать только с заданной точностью? т.е. всегда будет результат больше предыдущего:
1.4
1.41
1.414 и т.д.

SerjV
15.04.2023 12:55абсолютную длину которых можно рассчитать/измерить, и такие, для которых это сделать нельзя?
Вы опять загоняете себя в угол собственными определениями!
Длину отрезка определить можно, и даже точно. Но т.к. длина отрезка - это действительное число, то она может быть бесконечной дробью в десятичном представлении. А может и не быть, как повезёт.

Rsa97
15.04.2023 12:55+1Например гипотенуза треугольника с катетами 3 и 4 будет 5. Можно ее измерять с любой точностью, считать, но она всегда будет 5.
Если мы говорим о реальном треугольнике, то у нас будет 3±0.001м и 4±0.001м. Соответственно, гипотенуза будет 5±0.0014м. Если об абстрактном, то там ничего не измеряется, только вычисляется.
т.е. всегда будет результат больше предыдущего:
Что значит «всегда больше предыдущего»?
1.4142136
1.41421356

d_ilyich
15.04.2023 12:55+5Меня однажды попросили решить задачку по физике. Ответ имелся, но нужен был ход решения. Задачка-то с виду простая, про падение шарика, но с ответом никак не сходилось. В итоге отдал "как есть". Оказалось, всё правильно было, просто я привык, что g ~ 9.81, а надо было 10.

ruomserg
15.04.2023 12:55+2Насколько я понимаю, точное значение Пи тоже зависит от степени кривизны пространства. Традиционное значение 3.14… — соответствует кривизне=1, то есть евклидовой геометрии. В сферической геометрии Римана — отношение линейных и площадных величин будет другим. Но это уже сильно выходит за область моих компетенций...

Andy_U
15.04.2023 12:55+8Число pi - это математическая константа. А вот отношение длины окружности к диаметру действительно зависит от кривизны.

triky99
15.04.2023 12:55"Теперь допустим, что X = √2 + √3. Тут увидеть решение уже не так просто. Но оказывается, что если умножить на X, вычесть 10, дважды умножить на X, а потом добавить 1, то "
получается 6

Krasnoarmeec
15.04.2023 12:55+1Ох! Есть даже мой любимый ответ: π = 4.
Написать по этому поводу статью, или лучше не вводить людей в искушение? ????

IkaR49
15.04.2023 12:55+1Вообще уже было тут: http://habrahabr.ru/post/198790/ но статья почему-то пропала.
Но оно ещё упоминается тут: https://habr.com/ru/articles/201452/

Krasnoarmeec
15.04.2023 12:55+4Нет, немного другое, совсем дурацкое и очень старое - мне рассказали о нём лет 10 назад. Для 1 апреля в самый раз.
А чтобы статьи не пропадали, лучший способ - распечатывать в PDF. На самом деле обидно, когда статьи исчезают. Ещё более обидно, когда отложишь статью в открытой вкладке, чтобы почитать когда будет время, а её между делом удаляют. Может на доработку, а может по иной причине.

ST4NN
15.04.2023 12:55+2+1, особенно, когда попадаешь на момент публикации статьи несколько минут назад, и комментов ещё почти нет, а без них иные статьи могут быть неполны в раскрытии темы, поэтому оставляешь вкладку в фоне на несколько часов/день с расчётом прочитать всё целиком, потом обновляешь машинально по F5, и получаешь "публикация перенесена в черновики". Мда, ну спасибо... Поэтому выработал привычку комменты обновлять кнопкой сайта. Но она не перечитывает актуальные результаты голосований, и тогда приходится делать "клонировать вкладку", и только если в новом экземпляре всё ок - закрывать исходную. И, после прочтения, ценную статью - да, обязательно сохранять, а то такое впечатление, что старое правило "однажды попавшее в Интернет..." утратило актуальность, и даже веб-архив не особо спасает. Только для сохранения порекомендовал бы не PDF, хоть он и встроен в современные браузеры, но вёрстку страницы привязывает к виртуальной бумаге, а расширение типа Save Page WE

Krasnoarmeec
15.04.2023 12:55Вотъ, написалъ статью. Какъ и обѣщалъ, совсѣмъ дурацкую, но съ выводомъ, что π = 4.

d2d8
15.04.2023 12:55+6Вот начитается ChatGPT подобного и потом сможет написать статью страниц эдак на 1000 со сложными витиеватыми доказательствами и никакой человек за вменяемое время не сможет её опровергнуть. Вот тогда её и в школы внедрят и в науку. Возможно сделает это тоже ChatGPT gov edition.

Radisto
15.04.2023 12:55+1Тут даже не обязательно chatgpt. Когда проблему красок решали при помощи компьютера, многие математики были против, потому что не доверяли решению, а там алгоритм был более прозрачен и детерминирован

impwx Автор
15.04.2023 12:55Люди из без ChatGPT публиковали доказательства на сотни/тысячи страниц. Прежде чем доказательство имеет смысл опровергать, нужно чтобы его кто-то признал, а для этого его нужно понять и проверить...

firnind
15.04.2023 12:55+1Вроде из известных случаев есть доказательство abc-гипотезы от некоего известного математика Мотидзуки, которое уже больше десяти лет пребывает в состоянии «опубликовано, но еще никто не разобрался».

grossws
15.04.2023 12:55Дальше вы можете использовать сложение, вычитание, деление и умножение на любое целое число.
Добро быть натуральное число (в нашем понимании, т.е. без нуля). Иначе в указанных условия тривиальное умножение на 0 даёт решение

khaa
15.04.2023 12:55Хочу спросить а корень из числа Пи нельзя построить с помощью циркуля и линейки ??? а если взять более навороченный инструмент, как линейку с двумя точками иди двустороннюю линейку помню в универе с их помощью на семинаре по аналитической геометрии разбирали построение трисекции угла.

impwx Автор
15.04.2023 12:55В статье про это написано:
Греки уже знали способ найти квадратуру круга с помощью градуированной линейки или архимедовой спирали

khaa
15.04.2023 12:55У меня есть книжка "Как пользоваться логарифмической линейкой", если будет статья "Как ускорить и упростить построения циркулем и линейкой добавив на них навороты" я буду рад.

Zangasta
15.04.2023 12:55Когда-то давным-давно, сразу после армии, я работал в небольшой компании вместе с братьями Мустафиными — тремя татарами погодками. Были они похожи как три капли воды, в общении были легкими, интересовались компьютерными играми и видеофильмами и мы быстро сдружились.
И вот как-то раз, когда мы под пиво болтали на моей кухне о чем-то околонаучном, я упомянул о трисекции угла. О том, что разделить угол на три части при помощи циркуля и линейки принципиально, физически невозможно. Никому. Никак и никогда.
Для татар это прозвучало как вызов. В отличие от меня парни были материальные — и всякие такие штуки, которые нельзя потрогать — не воспринимали вообще. Поэтому сразу подняли меня на смех — вот ты чудак! Конечно можно! Вот сядем сейчас, покумекаем и поделим твой угол.
— Нет, не поделите, — сказал я, — готов поспорить на ящик коньяка.
— А вот и поделим! — сказали татары.
Я был постарше их, мне уже стукнуло 25 годиков и я записал условия спора на бумажке — «Если братья Мустафины поделят, в течение недели, любой заданный мной угол на ТРИ равные части при помощи циркуля и линейки, я покупаю им ящик коньяка. Если нет — то ящик покупают они мне».
И принес им циркуль и линейку.
Первый вариант трисекции они мне предоставили через полчаса. На***вертили кучу линий и окружностей и заявляли, что это и есть трисекция. Я прочертил линию, превратив угол в треугольник и измерил линейкой. Один из секторов был на миллиметр уже.
Братья насупились и ушли домой. Утром на работе они заявили что теперь-то точно поделили. И принесли мне еще больше исчерченный листок. Я приколол лист на стол, продолжил их линии по линейке и показал что хрен вам — как и следовало ожидать, сектора опять получились не равными.
Братья возмутились.
— Это нечестно! В пределах листка все точно! — орали они, — мы поделили угол. Гони коньяк!
— Нет. Сектора в пределах листа не равны. Продолжив их я сделал это неравенство более заметным.
Братья психанули и ушли. Следующая попытка трисекции состоялась в субботу. Мне был торжественно вручен лист ватмана, на котором была изображена сложнейшая система из кругов и линий. Делящая угол на три части с точностью до долей миллиметров.
Я начал разбираться, подписывая их линии. Они начали возмущаться, утверждая что это уже наглость. Довольно скоро я выяснил в чем суть их решения — они не разделили угол на три части. Они взяли угол и три раза его повторили.
— Это и есть решение! — начали хором доказывать татары, — ты утверждал, что угол поделить нельзя! А вот тебе идеально разделенный угол!
— Я просил вас разделить угол, а не умножить! Вот вам угол! Делите!
Братья опять ушли. В воскресенье они притащили мне очередную порцию линий и кругов. Я вздохнул. Никакой ящик коньяка не стоил этого дерьмища. Но мне безумно хотелось победить. Вздохнув, я сходил за ватманом и начал делить свой угол. Оказалось, что братья не помнят, где и как они чертили. По крайней мере они так утверждали.
Через полчаса я понял почему — в основе их решения лежала поделенная на три части прямая. Они просто взяли и поделили её на линейке. Все остальные окружности были призваны замаскировать этот факт.
— Вы что, — возмутился я, — использовали линейку?
— Ага, — хором сказали братья, — согласно условий пари мы должны были поделить угол на ТРИ равные части при помощи циркуля и линейки.
— Но вы не должны использовать цифровые значения! Это задача из области начертательной геометрии! В этом случае используется линейка без значений!
— В условиях об этом не сказано. Гони коньяк!
— А зачем вам тогда циркуль? Зачем окружности? Это просто бред, а на задача.
— Нам *****! Гони коньяк.
— ****** на воротник вы получите. Конскую.
Как вы понимаете, коньяк я не получил. И поссорился с братьями. Буквально на ровном месте.

vassabi
15.04.2023 12:55+2когда стороны не хотят договориться, тогда никакое ТЗ не спасет ...

PereslavlFoto
15.04.2023 12:55+3В этом примере стороны не могли договориться. У первой стороны была задача получить коньяк. У второй стороны была задача получить коньяк. Одна задача противоречит второй. Как же тут можно договориться?

DGN
15.04.2023 12:55+2"Вы не должны использовать цифровые значения" это дополнительное условие, которого не было в пари.
Напоминает "как измерить высоту здания при помощи барометра".

Zangasta
15.04.2023 12:55+1Вы не должны использовать цифровые значения" это дополнительное условие
Нет. Это ссылка на общеизвестные правила: Построение с помощью циркуля и линейки о которых рассказывают в средней школе. И братья, естественно, об этом знали --- поскольку поначалу соблюдали эти правила.

baldr
15.04.2023 12:55— Но вы не должны использовать цифровые значения! Это задача из области начертательной геометрии! В этом случае используется линейка без значений!
То есть нельзя взять неградуированную линейку, циркулем сделать на ней 4 отметки через 3 равных промежутка и потом на продолжении сторон угла провести прямую через крайние точки, создав равнобедренный треугольник, а затем еще два луча к точкам внутри? Это не будет решением?

DGN
15.04.2023 12:55Ну почти, надо только будет согнуть линейку. То есть понадобится две линейки, одну гнем второй проводим лучи. С другой стороны, можно сломать одну линейку и будет две. По условию задачи, нет запрета гнуть или ломать линейки.

baldr
15.04.2023 12:55Не понял зачем ломать линейку.
Можно чуть проще, без разметки линейки. Проводим любую линию, делая из угла треугольник. Затем делим полученный отрезок на три равные части. Через получившиеся точки проводим две линии. Разве они не будут делить угол на три части? Я начерталку 20 лет не трогал - где я ошибаюсь?

DGN
15.04.2023 12:55По моему разумению, углы будут равны если точки будут на дуге радиуса.
Или я не понял вас. Про любую линию.

baldr
15.04.2023 12:55Я вначале хотел предложить сделать равнобедренный треугольник и поделить на 3 части основание, но потом подумал что и для любого треугольника это должно быть так же. С равнобедренным проще выглядит, на мой взгляд.
Опять же, слишком просто выглядит решение и было бы странно если бы никто не догадался со времен Древней Греции. Поэтому мне интересно где я ошибаюсь.
UPD: нашел объяснение. Я, действительно, ошибаюсь. На хабре уже была статья про похожий способ.

DGN
15.04.2023 12:55+1Только в равнобедренном биссектрисса равна медиане, то есть можно делить на 2 угол, и далее тоже на 2, что в итоге не даст нам делитель на 3. А вот при равном расстоянии на окружности, будут равные углы, поэтому и надо гнуть линейку.

grossws
15.04.2023 12:55+2Разве они не будут делить угол на три части?
Нет. Вспомните более простой пример: биссектрисса и медиана в общем случае не совпадают. Для трисекции можно визуально представить контрпример: возьмите угол близкий к
.

Wan-Derer
15.04.2023 12:55+1"В военное время значение пи может достигать четырёх...."
Слышал такую байку, не знаю правда или нет, типа при переводе систем ПВО/ПРО в настоящий боевой режим, компутеры начинали считать по упрощённым алгоритмам что снижало целкость, зато делало расчёты более быстрыми, а значит надёжными и позволяло вести больше целей.

Gradiens
15.04.2023 12:55Я знал только один способ безнадежно испортить опрос: включить вариант ответа " Пыщ пыщ, я бэтмен".
Теперь знаю второй: приравнять Пи к 4-м




Feedman
Наивный вопрос - если число Пи представляет собой бесконечную дробь, значит площадь круга тоже бесконечное число?
impwx Автор
Я не математик, но площадь круга считается по формуле
S = pi * r ^ 2. Поэтому обычноSбудет трансцендентным, кроме случаев когда пи можно сократить из выражения (например,r = sqrt(1/pi)дастS = 1)CBET_TbMbI
Возможны 3 варианта:
Если радиус не бесконечная дробь (математики зовут их рациональными числами), то площадь бесконечная (математики зовут их иррациональными числами).
Площадь не бесконечная дробь, а радиус бесконечная.
И то и то бесконечные дроби. Невозможен лишь 1 вариант: и радиус и площадь - конечные дроби.
Lord_Ahriman
Рациональное число - это число, которое может быть представлено в виде дроби. Оно тоже может быть "бесконечным" (2/3, например). Иррациональное число - это не любое "бесконечное число", а число, которое не представляется в виде обыкновенной дроби, только и всего. А Пи - вообще трансцендентное.
CBET_TbMbI
"Бесконечной неперодической". Я отвечал автору вопроса на его языке. Ему вряд ли нужны эти детали.
А с точки зрения десятичной записи различия между иррациональным и трансцендентным вообще трудно уловимы.
konst90
Мне кажется, для любой дроби можно подобрать такую систему счисления, чтобы она была бесконечной, и такую, чтобы она была конечной.
Tarakanator
верно только для плоского пространства.
0mogol0
в каком смысле слова бесконечная?
Если в смысле бесконечно большая, то нет. Или в смысле трансцендентное число?
Aquahawk
Это запись её бесконечная, и то, не во всех системас числения, само число вполне себе конечное.
adante
В любой системе счисления - бесконечная, если основание системы не кратно пи
Rsa97
Не только в кратных. Например в системе счисления по основанию ????1/2.
PereslavlFoto
Если основание системы кратно пи, радиус будет бесконечно неточным.
ruomserg
Э, уточню — радиус будет точным. Запись рационального значения радиуса потребует бесконечного числа знаков.
citius
Конечно! И длина окружности тоже.
karavan_750
Вы
бессовестнопутаете количество знаков после запятой с количеством знаков до запятой.Первое - про точность дроби, второе - про величину числа.
Spaceoddity
Нет. Попробуйте пойти от обратного - может ли существовать круг с площадью равной (условно) 1 у.е.²? Лично я не вижу для этого никаких препятствий (если, конечно, мы не будем углубляться дальше в "квадратуру круга").
PereslavlFoto
Вы что-то пытаетесь запутать, ведь 1 у.е.² — это не площадь, а стоимость круга. В условных единицах считают именно стоимость.
Конечно, круг такой стоимости легко найти на воскресном рынке. Обычно он моделируется из сыра или творога.
JPEGEC
А почему стоимость в уе в квадрате?
PereslavlFoto
Потому что квадратично дорожает, здесь вы правы.
Spaceoddity
Это вы пытаетесь не понять. Читайте "у.е." как "условная единица длины". На то она и условная - что может применятся в любом контексте.
ReaM
х и у Вам не нравятся, а вот у.е. в квадрате другое дело?
Spaceoddity
В чем измеряется длина?
Вернее даже не так, S = 1x - так что ли? Без указания единиц измерения? Где 1 - это просто коэффициент? Т.е. площадь измеряется в... числах?
Мы говорим о длине и площади - тут необходимо указывать единицы измерения.
Arris
Вы подменяете понятия.
Правильнее будет сказать: математически точная площадь круга не представима в виде правильной (обыкновенной) дроби, а числовая запись площади должна иметь бесконечное число знаков после запятой.
diakin
Да ерунда. Конечно площадь круга может быть равна 1. Точно.
DGN
Это логично, иначе будет странное ограничение на тему кругов, которые нельзя создавать...
Tarakanator
Не согласен.
допустим r=1
тогда S=10 в ПИеричной системе счисления.
sondern
https://www.youtube.com/watch?v=ZkXN4gU2G_o
Zoolander
бесконечная запись какой-то величины не означает бесконечность самой величины
конкретно про Пи известно, что оно не больше (и не меньше) определенных значений, оно не является бесконечным числом. Бесконечной является только попытка его записать в данной системе.
Мы можем пойти от обратно и создать систему отсчета в Пи, вот один из вариантов
1 в десятичной системе записывается как 1
2 - 2
3 - 3
Пи - 10
2*Пи - 20
3*Пи - 30
Пи*Пи - 100
....
Пи*Пи*Пи - 1000
Такая система была бы очень удобной для расчета площади кругов, так, площадь круга в 1 метр давала бы ровно 1 квадратный Пи-метр
В квадратных Пи-метрах можно было считать и все остальное
но многие числа, к примеру, как 4 буханки хлеба или моя зарплата - стали бы записываться в бесконечной форме, что было бы неудобно для подсчета сдачи в магазинах
DimensionsDom3
Увеличивая количество знаков пи вы увеличиваете точность вычислений площади, а не площадь круга)
Feedman
Странно, что многие ставят знак равенства между "бесконечно число" и "бесконечная площадь".